انتگرال ریمان — به زبان ساده

در یکی از شاخه‌های ریاضیات به نام «آنالیز حقیقی» (Real Analysis)، بحث در مورد انتگرال و انتگرال‌پذیری مورد بررسی قرار می‌گیرد. یکی از انواع روش‌های انتگرال‌گیری توسط «برنهارد ریمان» (Bernhard Riemann)، ریاضیدان آلمانی ابداع شد که البته کاربرد زیادی در علوم دیگر و همچنین ریاضیات دارد. به همین مناسبت موضوع این نوشتار از مجله فرادرس را مفهوم انتگرال ریمان در ریاضیات انتخاب کرده‌ایم تا با شیوه انتگرال‌گیری ریمان و ویژگی و محدودیت‌های آن آشنا شویم.

برای آشنایی بیشتر با موضوع انتگرال و روش‌‌های انتگرال‌گیری، بهتر است مطالب انتگرال و محاسبات آن — به زبان ساده و انتگرال ریمان استیلتیس (Riemann Stieltjes) — مفاهیم و کاربردها (+ لینک) را مطالعه کنید. همچنین خواندن نوشتارهای نظریه اندازه در ریاضیات — مفاهیم و کاربردها و انتگرال لبگ در ریاضیات | به زبان ساده نیز خالی از لطف نیست.

مفهوم انتگرال ریمان در ریاضیات

در این نوشتار می‌خواهیم با مجموع ریمانی و همچنین انتگرال ریمان آشنا شویم. انتگرال ریمان در حقیقت اولین و معروف‌ترین شیوه محاسبه انتگرال روی یک فاصله است. ریمان این شیوه انتگرال‌گیری را در سال ۱۸۵۴ در «دانشگاه کوتینگن» (University of Göttingen)‌ مطرح کرد، ولی به دلایلی مقاله مربوط به آن را تا سال ۱۸۶۸ منتشر نکرد.

شیوه انتگرال‌گیری ریمان، برای بسیاری از توابع و کاربردها، به کار می‌رود و می‌توان آن را بوسیله «قضیه اساسی حساب» (Fundamental Theorem of Calculus) و همچنین «انتگرال‌گیری عددی» (Numerical Integration)، مورد ارزیابی و محاسبه قرار داد.

نکته: در بسیاری از مواقع در ریاضیات پیشرفته و آنالیز ریاضی، مفهوم انتگرال ریمان و نحوه محاسبه انتگرال به روش او، کارساز نیست و باید از محاسبه انتگرال با رویکرد «انتگرال ریمان-استیلتیس» (Riemann–Stieltjes integral) استفاده نمود.

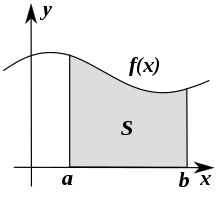
فرض کنید تابع $$f$$، یک تابع نامنفی و حقیقی-مقدار باشد که روی بازه $$[a,b]$$ تعریف شده است. ناحیه $$S$$ را در صفحه مربوط به نمودار تابع $$f$$ به شکلی در نظر می‌گیریم که شامل زوج مرتب‌هایی باشد که در آن بازه، مولفه دوم زوج مرتب، مقداری کوچکتر از تابع داشته باشد و مولفه اول نیز در فاصله بسته $$[a,b]$$ تغییر کند.

$$ \large S = \left \{ (x, y) \, : \ a \leq x \leq b, 0 < y < f(x) \right \| $$

انتگرال تابع $$f$$ در بازه $$[a,b]$$ در حقیقت سطح زیر منحنی تابع $$f$$ یا مساحت ناحیه $$S$$ خواهد بود. نمایش این سطح توسط نماد انتگرال به صورت زیر انجام می‌شود.

$$ \large \int_{a}^{b} f(x) \, dx $$

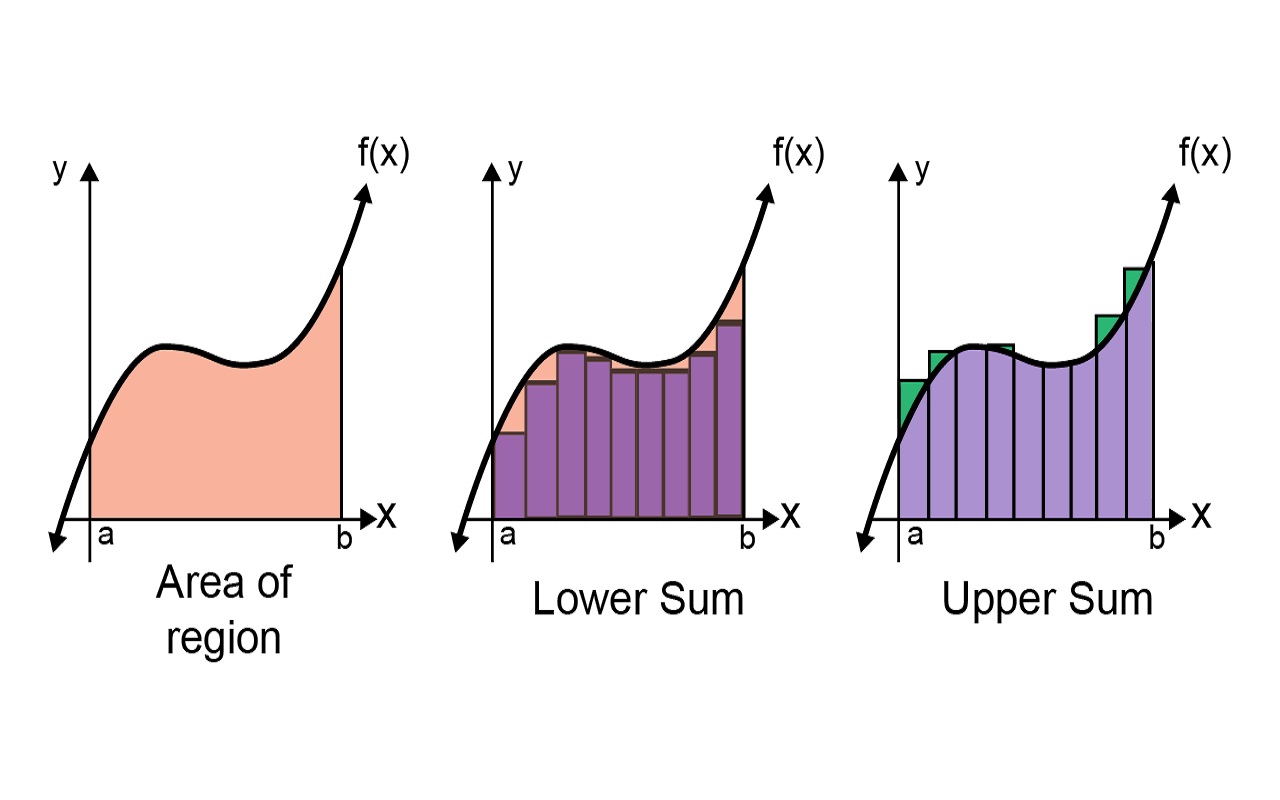
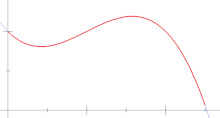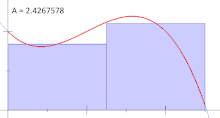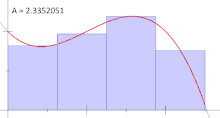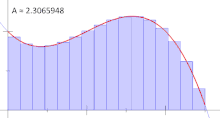
ایده‌ای که ریمان برای انتگرال ارائه داد، تعیین اندازه تقریبی مساحت $$S$$ به شیوه‌ای بسیار ساده بود. او مفهوم انتگرال را براساس حد مجموع مساحت‌های قطعه‌های کوچکی از مساحت کل در نظر گرفت که به سادگی قابل محاسبه بوده و این مجموع در حد با سطح زیر منحنی برابر است. در تصویر ۱، این مفهوم نمایش داده شده است.

نکته: توجه داشته باشید که اگر تابع $$f$$ هم شامل مقادیر مثبت و هم منفی باشد، آنگاه انتگرال برابر با مساحت (علامت‌دار) قسمت مثبت منهای مساحت قسمت منفی خواهد بود. به یاد داشته باشید که ناحیه بالا محور $$x$$، مساحت قسمت مثبت را ایجاد کرده و ناحیه زیر محور افقی نیز مساحت قسمت منفی را مشخص می‌کند. واضح است که مساحت قسمت منفی باید با علامت منفی مشخص شود.

تعریف رسمی انتگرال ریمان

با توجه به شیوه‌ای که ریمان برای مفهوم انتگرال ریمان ابداع کرد، قبل از هر چیز باید افراز (Partition) بازه $$[a,b]$$ را مشخص کنیم. زیرا این انتگرال وابسته به افرازها و اندازه آن‌ها است.

افراز بازه انتگرال‌گیری

ریمان بازه انتگرال‌گیری را به صورت دنباله‌ای متناهی از اعداد $$x_i$$ افراز یا تفکیک کرد. واضح است که این اعداد باید در رابطه زیر صدق کنند.

$$ \large { \displaystyle a = x_{0} < x_{1} < x_{2} < \dots < x_{n} = b } $$

هر فاصله بسته $$[x_i,x_{i+1}]$$ یک زیربازه (زیرفاصله) از افراز نامیده می‌شود. اندازه یا نرم هر افراز، براساس بزرگترین طول زیرفاصله‌های آن مشخص می‌شود. به این ترتیب نرم یا اندازه افراز به صورت زیر بدست می‌آید:

$$ \large { \displaystyle \max \left( x_{ i + 1 } – x_{i} \right) ,\quad i \in [ 0,n – 1 ] } $$

همچنین یک افراز نشاندار (Tagged Partition) که با نماد $$P(x,t)$$ روی بازه $$[a,b]$$ تعریف می‌شود، یک افراز به همراه دنباله‌ای از اعداد $$t_0 , t_1, \ldots,t_{n-1}$$ است که برحسب اندیس $$i$$ متمایز شده و داریم $$t_i \in [x_i,x_{i+1}]$$. به بیان دیگر افراز نشاندار، یک افراز است که به وسیله نقاط مجزایی از همه زیرفاصله‌ها، تعریف و معرفی می‌شود. طول هر افراز نشاندار، برابر با همان طول افراز عادی است.

دو افراز نشاندار $$P(x,t)$$ و $$Q(y,s)$$ را روی بازه $$[a,b]$$ در نظر داشته باشید. می‌گوییم $$Q(y,s)$$ ظریفتر از $$P(x,t)$$ است، اگر برای هر عدد صحیح $$i \in [0,n]$$ یک عدد صحیح مثل $$r(i)$$ وجود داشته باشد که $$x_i = y_{r(i)}$$ بوده و $$t_i = s_j$$ باشد. در این میان، بین $$i$$ و $$j$$ رابطه $$j \in [r(i),r(i+1))$$ برقرار است.

به بیان دیگر، افراز ظریفتر از یک افراز نشاندار، زیرفاصله‌ها را به بخش‌هایی دیگری تقسیم کرده بطوری که نشان‌های (Tag) بیشتر به افراز اضافه شده و در نتیجه افراز، ظریفتر از افراز اولیه است. این کار دقت در محاسبه تقریبی مساحت زیر منحنی (انتگرال) را بیشتر می‌کند.

می‌توان یک «ترتیب جزئی» (Partial Order) را برای مقایسه افرازهای نشاندار به این ترتیب در نظر گرفت و آن‌ها را به ترتیب ظریف‌بودن، مرتب کرد. با توجه به این موضوع، یک افراز نشاندار را بزرگتر یا برابر با افراز نشاندار دیگر در نظر می‌گیریم، اگر اولی ظریف‌تر از دومی باشد. واضح است که افراز ظریف‌تر دارای اندازه یا نرم کوچکتری نسبت به افراز اولیه است. ریمان، افرازها را برای محاسبه انتگرال به گونه‌ای ظریف می‌کند تا اندازه افراز، در حد، برابر با صفر باشد.

جمع‌های ریمان

«جمع ریمان» (Riemann Sum) تابع حقیقی مقدار $$f$$ روی بازه $$[a,b]$$ نسبت به افراز نشاندار $$x_0,\ldots,x_n$$ با نشانه‌های $$t_0,\ldots,t_{n-1}$$ به صورت زیر نشان داده می‌شود.

$$ \large {\displaystyle \sum _{ i = 0}^{ n – 1 }f( t_{i}) \left( x_{ i + 1 } – x_{i} \right) } $$

مشخص است که هر جمله از حاصل جمع، به صورت حاصل‌ضرب تابع $$f$$ در نقطه $$t_i$$ با طول فاصله یا اندازه زیربازه‌ای که $$t_i$$ به آن تعلق دارد (یعنی $$[x_i,x_{i+1}]$$)، نوشته شده است. پس می‌توان هر یک از جملات جمع را دنباله‌ای از مساحت‌های (علامت‌دار) مستطیل‌هایی با ارتفاع $$f(t_i)$$ با پهنای $$x_{i+1}-x_i$$ دانست. به این ترتیب جمع ریمان مجموع مساحت (علامت‌دار) این مستطیل‌ها خواهد بود.

همین مفهوم توسط «مجموع بالایی و پایینی درابوکس» (Upper and Lower Darboux Sum) نیز قابل توصیف است. ولی در اینجا نشانه ($$t_i$$) با سوپریمم (Sup) و اینفیمم (Inf) روی زیرفاصله‌ها جایگزین شده است. در ادامه مجموع پایینی و بالایی داربوکس با نمادهای $$L(f,P)$$ و $$U(f,P)$$ به ترتیب مشخص شده‌اند.

$$ \large {\displaystyle {\begin{aligned}L(f,P)& = \sum _{i = 0}^{n – 1}\inf _{t \in [x_{i},x_{i + 1}]}f(t)(x_{i + 1} – x_{i}),\\ U(f,P)& = \sum _{i = 0}^{n – 1}\sup _{t \in [x_{i},x_{i + 1}]}f(t)(x_{ i + 1 } – x_{i}).\end{aligned}} } $$

واضح است $$f$$، تابع و $$P$$ نیز افراز مورد نظر را نشان می‌دهند. اگر تابع $$f$$ پیوسته (Continuous) باشد، مجموع بالایی و پایین داربوکس با مجموع ریمان روی همان افراز (ولی به صورت نشان‌دار) برابر خواهد بود.

نکته: اگر تابع $$f$$ روی زیربازه‌ای ناپیوسته باشد، مقدار نشان $$t_i$$ ممکن است بزرگترین کران پایین (Inf) یا کوچکترین کران بالا (Sup) در زیربازه یاد شده نباشد.

انتگرال ریمان

با توجه به مفهوم ظریف‌تر کردن افراز و مجموع ریمان، انتگرال ریمان را حد مجموع ریمان در نظر گرفته، زمانی که افراز ظریف‌تر شود. اگراین حد موجود باشد، آنگاه تابع $$f$$ را انتگرال‌پذیر یا به بیان دقیق‌تر «انتگرال‌پذیر ریمان» (Riemann-integrable) می‌نامند.

یکی از فرض‌های اولیه در مفهوم انتگرال ریمان و محاسبه آن، کوچک‌ بودن اندازه زیرفاصله‌ها یا ظریف‌تر بودن افراز است بطوری که باید در حد اندازه زیرفاصله‌ها یا زیربازه‌ها به سمت صفر میل کند. اگر چنین امری رخ ندهد تقریب مناسبی برای اندازه انتگرال حاصل نخواهد شد.

پس می‌توان گفت انتگرال ریمان تابع $$f$$ برابر با $$s$$‌ است اگر شرط زیر برقرار باشد.

برای هر $$\epsilon >0$$، وجود داشته باشد $$\delta >0$$ بطوری که برای هر افراز نشان‌دار $$x_0,\ldots,x_n$$ و $$t_0,\ldots,t_{n-1}$$ با اندازه کمتر از $$\delta$$ داشته باشیم:

$$ \large \max_{i \in [ 0 , n ]} (x_{ i + 1 } – x_i) < \delta \rightarrow \left| \sum_{ i = 0 }^{n – 1} f(t_i) (x_{ i + 1 } – x_i) – s \right| < \varepsilon $$

متاسفانه تعریفی که براساس حد برای مفهوم انتگرال ریمان معرفی شد، شرایط سختی داشته که بررسی صحت آن‌ها به راحتی قابل بررسی نیست. بنابراین این شرط را به کمک شرایط دیگر که بررسی آن‌ها ساده‌تر هستند، جایگزین می‌کنیم. البته هم‌ارز بودن شرط اولیه با شرط‌های جدید طبق قضیه‌هایی قابل اثبات است. به این ترتیب تابع $$f$$ را برابر با $$s$$ در نظر می‌گیریم اگر شرایط زیر برقرار باشد:

برای هر $$\epsilon >0$$ یک افراز نشاندار $$y_0,\ldots,y_m$$ و $$r_0,\ldots,r_{m-1}$$ وجود دارد بطوری که برای هر افراز نشاندار $$x_0,\ldots,x_n$$ و $$t_0,\ldots,t_{n-1}$$ که از $$y_0,\ldots,y_m$$ و $$r_0,\ldots,r_{m-1}$$ ظریف‌تر است، داشته باشیم:

$$ \large \left|\sum_{ i = 0}^{n – 1} f(t_i) (x_{i + 1} – x_i) – s \right| < \varepsilon $$

مفاهیم مشابه با مفهوم انتگرال ریمان

برای مشخص کردن مفهوم انتگرال ریمان و شیوه محاسبه آن، معمولا انتگرال ریمان را برحسب «انتگرال داربوکس» (Darboux Integral) بیان می‌کنند. البته این امر به علت سادگی روش به کار رفته در این انتگرال است. حتی می‌توان نشان داد که تابع $$f$$ انتگرال‌پذیر ریمان است اگر و فقط اگر انتگرال‌پذیر داربوکس باشد.

یکی از مفاهیم و قیدهای مربوط به انتگرال ریمان، مجموع ریمان «دست راست» (Right-hand) و «دست چپ» (Left-hand) است. در جمع سمت چپ ریمان برای هر $$i$$ خواهیم داشت $$t_i = x_i$$ در حالیکه در جمع سمت راست رابطه $$t_i = x_{i+1}$$ برقرار است. به این ترتیب مجموعه جمع‌های دست چپ ریمان و مجموعه جمع‌های دست راست روی افراز یا فاصله تفکیک شده علامت‌دار یک شکل خواهند بود.

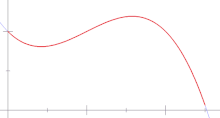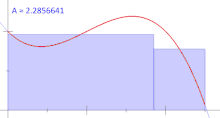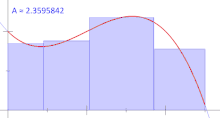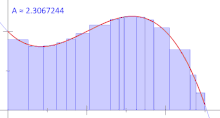
یکی دیگر از قیدهای مهم در انتگرال ریمان، ایجاد زیر فاصله‌ها است. برای مثال یک زیرفاصله با قاعده برای فاصله $$[0,1]$$ با در نظر گرفتن $$n$$ زیرفاصله به صورت زیر است:

$$ \large {\displaystyle \left[ 0, { \frac {1}{n}} \right], \left[ {\frac {1}{n}},{ \frac {2}{n} } \right], \ldots ,\left[ { \frac {n-1}{n} }, 1 \right] } $$

اهمیت این گونه ایجاد کردن افرازها، در تعیین مجموع دست چپ و راست ریمان است. استفاده از فقط مجموع دست چپ یا دست راست ریمان در محاسبه انتگرال ریمان، خطرناک است و ممکن است محاسبات را دچار بیش یا کم برآوردی کند. افراز با قاعده را در تصویر ۴ برای محاسبه انتگرال ریمان، مشاهده می‌کنید.

البته اگر از قبل بدانیم تابع $$f$$، انتگرال‌پذیر ریمان است محاسبات مشکلی نخواهند داشت ولی با توجه به شرایط گفته شده، تابع نشانگر اعداد گویا $$I_Q$$، یک تابع انتگرال‌پذیر ریمان روی بازه $$[0,1]$$ تلقی خواهد شد که حاصل انتگرال برابر با ۱ است.

در تابع نشانگر اعداد گویا، در نظر بگیرید که هر یک از نقطه‌های انتهایی مربوط به زیرفاصله‌ها یک عدد گویا باشند. در نتیجه مقدار تابع همیشه در نقطه‌های گویا بدست آمده و برابر با ۱ خواهد بود. مشکل زمانی رخ می‌دهد که بخواهیم انتگرال تابع نشانگر گویا را به دو انتگرال تبدیل کنیم. فرض کنید نقطه شکست $$\sqrt{2}-1$$ باشد.

$$ \large { \displaystyle \int _{0}^{{ \sqrt {2}}-1} I_{ \mathbb {Q} }(x)\, dx + \int _{ { \sqrt {2}} – 1 }^{1}I_{ \mathbb {Q} }(x)\, dx = \int _{0}^{1} I_{\mathbb {Q} }(x) \, dx.}$$

اگر از تقسیم یا افراز با قاعده (Regular) یعنی تقسیم فاصله به $$n$$ زیرفاصله با طول‌های مساوی، برای محاسبه مجموع راست و چپ ریمان استفاده کنیم، هر دو جمله سمت راست تساوی صفر خواهند شد زیرا نقطه انتهایی (ابتدایی) هر زیرفاصله (به جز ۰ و ۱) یک عدد غیرگویا است که تابع نشانگر گویا را صفر می‌کنند. از طرفی سمت راست عبارت بالا برابر با ۱ است. این تناقض باعث می‌شود که تابع $$I_Q$$ انتگرال‌پذیر ریمان نباشد. ولی می‌دانیم چنین تابعی، «انتگرال‌پذیر لبگ» (Lebesgue Integrable) بوده و حاصل انتگرال آن در بازه $$[0,1]$$ برابر با صفر است.

خواص انتگرال ریمان

با توجه به مفهوم انتگرال ریمان و شیوه محاسبه آن، ویژگی و خصوصیات جالبی برای آن وجود دارد. در ادامه به خاصیت‌ها رابطه خطی و انتگرال‌پذیری ریمان خواهیم پرداخت.

خاصیت خطی انتگرال ریمان

با توجه به مفهوم انتگرال ریمان می‌توان آن را دارای خاصیت تبدیل خطی دانست. این امر به این معنی است که اگر $$f$$ و $$g$$ دو تابع انتگرال‌پذیر ریمان روی بازه $$[a,b]$$ باشند و $$\alpha$$ و $$\beta$$، مقادیر ثابتی در نظر گرفته شوند، خواهیم داشت:

$$ \large { \displaystyle \int _{a}^{b}( \alpha f(x) + \beta g(x)) \, dx = \alpha \int _{a}^{b}f(x)\,dx + \beta \int _{a}^{b}g(x) \,dx} $$

از آنجایی که حاصل انتگرال ریمان یک تابع، به صورت یک عدد بیان می‌شود، انتگرال ریمان یک «تابعک خطی» (Linear Functional) روی «فضای برداری» (Vector Space) توابع انتگرا‌ل‌پذیر خواهد بود. این ویژگی برای «انتگرال ریمان-استیلت‌یس» (Riemann–Stieltjes integral) نیز وجود داشته که راهگشای تعریف «امید ریاضی» (Mathematical Expectation) برای متغیر تصادفی است.

انتگرال‌پذیری ریمان

یک تابع کراندار (Bounded)، روی «فاصله فشرده» (Compact Interval) به صورت $$[a,b]$$ «انتگرال‌پذیر ریمان» (Riemann Integrable) است، اگر و تنها اگر، «تقریبا همه جا» (Almost everywhere)، پیوسته (Continuous) باشد. این امر به این معنی است که مجموعه نقاط ناپیوستگی برحسب اندازه لبگ، دارای اندازه صفر است. این ویژگی را گاهی «شرط انتگرال‌پذیری لبگ» (Lebesgue’s integrability condition) یا «محدودیت لبگ برای انتگرال‌پذیری ریمان» (Lebesgue’s criterion for Riemann integrability) می‌نامند.

نکته: فاصله فشرده در «توپولوژی» (Topology)، تعمیم فاصله بسته یا ناحیه مستطیلی در «فضای اقلیدسی» (Euclidean Space) است به شکلی که نقاط حدی یا مرزی در فاصله قرار دارند.

این قید یا محدودیت، زمانی که از فاصله و انتگرال لبگ استفاده می‌کنیم، هیچ مسئله‌ای ایجاد نمی‌کند. ولی زمانی که با اندازه عمومی غیر از اندازه لبگ سر و کار داشته باشیم، شرط انتگرال‌پذیری ریمان دارای اهمیت می‌شود.

خلاصه و جمع‌بندی

در این نوشتار به مفهوم و نگرش انتگرال ریمان به وسیله همگرایی جمع‌های ریمانی پرداختیم. همانطور که خواندید در صورتی که بزرگترین کران پایین (Infimum) و کوچکترین کران بالا (Supremum) مجموع ریمان یک فرم از تابع برابر و همگرا باشد، جمع ریمان را همگرا گفته و مقدار همگرایی همان انتگرال ریمان تابع است. از طرفی انتگرال ریمان با مجموع داربوکس نیز در ارتباط است. در این متن همچنین ویژگی‌ها ترکیب خطی و انتگرال‌پذیری ریمان مورد بررسی و کنکاش قرار گرفت.

هر چند نگرش ریمان به انتگرال و سطح زیر منحنی جالب به نظر می‌رسد ولی در بعضی از مواقع، امکان استفاده از آن برای محاسبه سطح زیر منحنی وجود ندارد. برای مثال تابع نشانگر اعداد گویا، در مفهوم انتگرال ریمان قابل محاسبه نبوده در حالیکه با انتگرال لبگ مقدار سطح زیر منحنی برای این تابع بدست می‌آید.