گرادیان (Gradient) در ریاضیات – به زبان ساده

عبارت گرادیان در ریاضیات، معانی متفاوتی دارد. ساده‌ترین آن، مفهومی مشابه با شیب خط است. در واقع برای محاسبه شیب یک نمودار و یا تغییرات یک تابع می‌توان از مفهوم گرادیان استفاده کرد. گرادیان در حالت عمومی در تحلیل برداری، یک عملگر برداری است که با نماد ∇ نمایش داده می‌شود. این عملگر، روی یک تابع اسکالر عمل می‌کند و در نهایت، حاصل آن به فرم یک بردار در می‌آید. گرادیان و دیورژانس از مهم‌ترین مفاهیم ریاضیات پایه هستند.

این مطلب، ابتدا به صورت جامع مفهوم گرادیان، روابط حاکم بر آن و کاربرد آن در علوم مختلف را مورد مطالعه قرار می‌دهد و در ادامه، روابط حاکم بر این مفهوم در مختصات کارتزین، استوانه‌ای و کروی بیان بیان می‌شود. همچنین در انتهای مطلب، با استفاده از چند مثال، کاربرد این روابط و شیوه محاسبه گرادیان یک تابع مورد بررسی قرار می‌گیرد.

گرادیان چیست؟

گرادیان در حالت عمومی در تحلیل برداری، یک عملگر برداری است که با نماد ∇ نمایش داده می‌شود. این نماد به عملگر «دل» (Del) و «نابلا» (Nabla) معروف است.

محاسبه گرادیان یک تابع حقیقی و اسکالر f، با اعمال عملگر دل روی آن تعریف می‌شود. این تابع با استفاده از نماد زیر نشان داده می‌شود.

$$\large f ( u_1 , u_2 , u_3 )$$

همانطور که توضیح داده شد، گرادیان این تابع به شکل زیر نمایش داده می‌شود.

$$\large \bigtriangledown f = grad (f)$$

در حالت کلی، گرادیان تابع دلخواه در سه راستا در «مختصات خمیده خط» (Curvilinear coordinates) به شکل زیر قابل نمایش است.

$$\large \bigtriangledown \phi = { 1 \over h_1 } { \partial \phi \over \partial u_1 } {\widehat{u}_1} + { 1 \over h_2 } { \partial \phi \over \partial u_2 } {\widehat{u}_2} + { 1 \over h_3 } { \partial \phi \over \partial u_3 } {\widehat{u}_3}$$

گرادیان این تابع را می‌توان در دستگاه «مختصات کارتزین» (Cartesian coordinate) به شکل زیر تعریف کرد.

$$\large \bigtriangledown \phi (x, y, z) = { \partial \phi \over \partial x } {\widehat{x}} + { \partial \phi \over \partial y } {\widehat{y}} + { \partial \phi \over \partial z } {\widehat{z}}$$

در صورتی که j ،i و k بردارهای یکه در جهت y ،x و z محور مختصات در نظر گرفته شوند، گرادیان در مختصات کارتزین به شکل زیر نمایش داده می‌شود.

$$\large \bigtriangledown f = { \partial f \over \partial x } { i } + { \partial f \over \partial y } { j } + { \partial f \over \partial z } { k }$$

اندازه گرادیان تابع دلخواه f را با نماد $$| \bigtriangledown f \enspace |$$ نمایش می‌دهند.

مثال

تابع f را به فرم $$f ( x , y , z ) = 2 x + 3 y^{ 2 } - sin ( z )$$ در نظر بگیرید. گرادیان این تابع را در مختصات کارتزین محاسبه کنید.

برای محاسبه گرادیان این تابع، ابتدا باید رابطه گرادیان در مختصات کارتزین نوشته و سپس مشتق جزئی این تابع در سه راستا محاسبه شود. در نهایت گرادیان این تابع به فرم زیر در می‌آید.

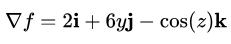
کاربرد گرادیان

فرض کنید که تابع اسکالر دما در یک محیط به صورت $$T ( x , y , z)$$ تعریف شده باشد.

توزیع دما در این محیط را می‌توان با استفاده از صفحات دما ثابت بیان کرد. هندسه این صفحات هم دما با استفاده از رابطه زیر محاسبه می‌شوند.

$$\Large T ( x , y , z ) =$$ ثابت

در این شرایط، می‌توان کانتورهای دما ثابت را برای دماهای متفاوت رسم کرد. در این صورت اگر در نقطه‌ای با مختصات $$\overrightarrow { r }$$ قرار داشته باشیم و به نقطه‌ای دیگر از این کانتورهای هم دما حرکت کنیم، دما تغییر می‌کند. در این حالت، تغییر دما بین دو نقطه $$P ( x , y , z)$$ و $$Q ( x + \Delta x , y + \Delta y , z + \Delta z)$$ با استفاده از رابطه زیر محاسبه می‌شود.

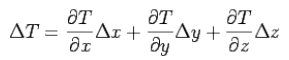
توجه کنید که مشتق‌ها در رابطه بالا، مشتقات جزئی را نشان می‌دهند. این موضوع در شکل زیر به تصویر کشیده شده است.

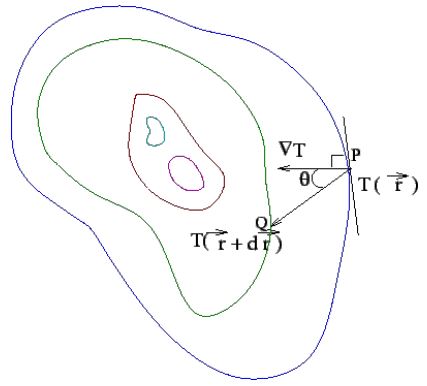
در صورتی که مقدار جابه‌جایی بسیار کوچک باشد، رابطه بالا را می‌توان به شکل زیر بازنویسی کرد.

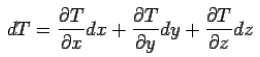
توجه کنید که تغییرات دما که با استفاده از عبارت dT در رابطه بالا نشان داده شده، شامل تغییرات دما در هر سه راستای محورهای مختصات است. این تغییرات را می‌توان با استفاده از بردار گرادیان که روابط آن در قسمت قبل بیان شد نیز نمایش داد. در این شرایط گرادیان تابع اسکالر دما به شکل زیر بیان می‌شود.

$$\large \bigtriangledown T = { \partial T \over \partial x } \widehat { i } + { \partial T \over \partial y } \widehat { j } + { \partial T \over \partial z } \widehat { k }$$

گرادیان در دستگاه مختصات استوانه‌ای

همانطور که اشاره شد، گرادیان را می‌توان در دستگاه‌های مختصات متفاوت بیان کرد، در قسمت قبل رابطه گرادیان در دستگاه مختصات کارتزین بیان شد. رابطه گرادیان تابع دلخواه f در دستگاه مختصات استوانه‌ای در این قسمت و مطابق با رابطه زیر تعریف می‌شود.

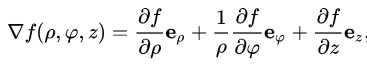
همانطور که مشاهده می‌شود، سمت راست این عبارت شامل سه ترم است. ترم اول، گرادیان در راستای شعاعی را نشان می‌دهد. ترم دوم نشان‌ دهنده گرادیان در راستای زاویه‌ای است و ترم سوم جهت عمود بر صفحه‌ای را نشان می‌دهد که بردارهای e_ρ و e_φ در آن قرار دارند. این سه راستا در شکل زیر برای یک نقطه دلخواه به صورت دقیق نمایش داده شده‌اند.

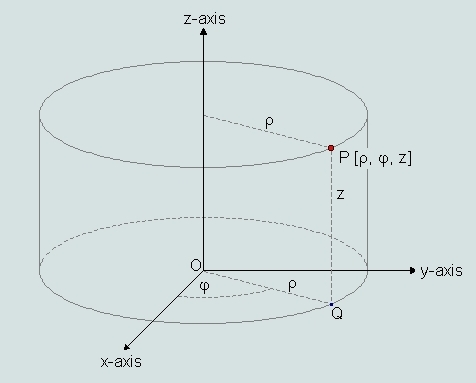
مقادیر نشان داده شده در شکل بالا را می‌توان با استفاده از مختصات یک نقطه در دستگاه مختصات کارتزین محاسبه کرد. روابط زیر ارتباط بین دستگاه مختصات استوانه‌ای و کارتزین را مورد بررسی قرار می‌دهند و از این روابط می‌توان برای تحلیل بهتر نتایج در دستگاه مختصات استوانه‌ای، بهره گرفت.

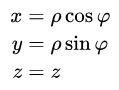
گرادیان در دستگاه مختصات کروی

روابط حاکم بر گرادیان در دستگاه مختصات کارتزین و استوانه‌ای، در بخش‌های قبل مورد بررسی قرار گرفتند.

در این قسمت به بررسی روابط حاکم بر گرادیان در دستگاه مختصات کروی پرداخته می‌شود. گرادیان یک تابع دلخواه f در این دستگاه به شکل زیر تعریف می‌شود.

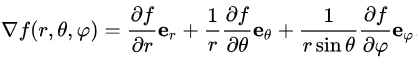
این رابطه در سه راستای θ ،r و φ بیان شده که شیوه نمایش این سه راستا در شکل زیر مورد مطالعه قرار گرفته است.

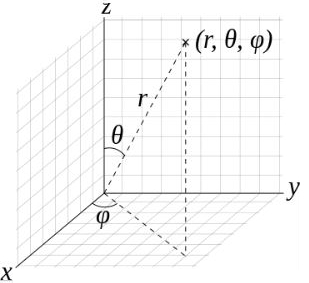
در صورتی که نیاز باشد که اعداد دستگاه مختصات کارتزین به دستگاه مختصات کروی تبدیل شود می‌توان از روابط زیر استفاده کرد.

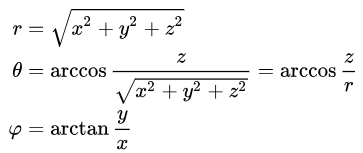
بنابراین در یک نقطه دلخواه از فضا، با استفاده از روابط بالا می‌توان فواصل و زوایای مورد نیاز دستگاه مختصات کروی را محاسبه کرد.

مثال‌ها

در بخش قبل، شیوه محاسبه گرادیان یک تابع اسکالر، در قالب یک مثال مورد مطالعه قرار گرفت.

در این قسمت چند مثال دیگر، برای فهم دقیق کاربرد این مفهوم مورد بررسی قرار می‌گیرند.

مثال ۱

تابع اسکالر f با استفاده از رابطه $$f ( x , y ) = x^ { 2 } y$$ تعریف می‌شود. در این شرایط گرادیان این تابع اسکالر را در نقطه $$( 3 , 2 )$$ محاسبه کنید.

گرادیان این تابع، یک بردار شامل مشتقات جزئی است. مشتق جزئی در راستای x در نقطه داده شده، به فرم زیر محاسبه می‌شود.

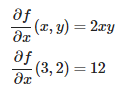
روند مشابهی را می‌توان برای مشتق جزئی در راستای y نیز مطابق با روابط زیر طی کرد.

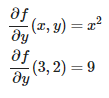
در نهایت می‌توان گرادیان این تابع در نقطه داده شده را به کمک مقادیر محاسبه شده مشتق جزئی، به شکل زیر بیان کرد.

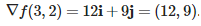
مثال 2

تابع f به فرم $$f ( x , y , z ) = x y e ^ { x ^ { 2 } + z ^ { 2 } - 5 }$$، نمایش داده می‌شود. گرادیان این تابع را در نقطه $$( 1 , 3 , - 2 )$$ محاسبه کنید.

گرادیان این تابع را می‌توان به صورت مشابه با مثال قبل، از طریق محاسبه مشتق‌های جزئی در سه راستای y ،x و z بیان کرد. بنابراین به صورت زیر عمل می‌کنیم.

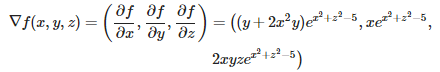
از آنجایی که گرادیان تابع مورد نظر در نقطه $$( 1 , 3 , - 2 )$$ خواسته شده است، این نقطه را در رابطه بالا قرار می‌دهیم. در نتیجه فرم نهایی گرادیان تابع f در نقطه $$( 1 , 3 , - 2 )$$ به شکل زیر در می‌آید.

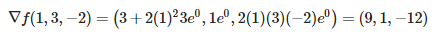
همانطور که اشاره شد، عملگر گرادیان، روی یک تابع اسکالر عمل می‌کند و در نهایت نتیجه آن به فرم یک تابع برداری محاسبه می‌شود. در مطلب دیورژانس وبلاگ فرادرس، تفاوت دیورژانس و گرادیان به صورت جامع مطالعه شده است. در این مطلب نشان داده شد که دیورژانس عملگری است که روی یک بردار اعمال می‌شود و در نهایت یک تابع اسکالر را تولید می‌کند، ولی گرادیان عملگری است که روی یک تابع اسکالر اعمال می‌شود و حاصل آن به صورت یک بردار در می‌آید که روابط و شیوه محاسبه گرادیان در این مطلب به صورت کامل بیان شده است.

این مطلب، ابتدا به صورت جامع به بررسی مفهوم گرادیان، روابط حاکم بر آن و کاربرد آن در علوم مختلف پرداخته است. در ادامه، روابط حاکم بر این مفهوم در مختصات کارتزین، استوانه‌ای و کروی بیان شد و در نهایت به کمک چند مثال، کاربرد این روابط و شیوه محاسبه گرادیان یک تابع مورد بررسی قرار گرفت.