حل معادله در اکسل — آموزش گام به گام

بسیاری از پدیدههای طبیعی بوسیله «معادلات (Equation) قابل توصیف هستند. برای مثال، معادله سقوط آزاد یک جسم، محاسبه سرعت یک واکنش شیمایی و غیره بوسیله معادلات بیان میشوند. روشهای حل معادلات ریاضی گسترده بوده و گاهی امکان حل آنها به صورت تحلیلی وجود ندارد. در این بین، شیوههای حل معادلات به صورت عددی و حتی تقریبی مناسب است. اکسل نیز به ابزار حل معادلات به شیوه عددی مجهز است. در این نوشتار به بررسی حل معادله در اکسل به صورت گام به گام خواهیم پرداخت و با سه راه حل یا تکنیک مختلف، مراحل اجرایی را پی میگیریم.
به منظور آشنایی بیشتر با اکسل و معادلات، نوشتارهای معادله منحنی در اکسل | به زبان ساده و فرمول نویسی در اکسل — به زبان ساده را مطالعه کنید. همچنین خواندن نوشتارهای سیمپلکس در اکسل — راهنمای کاربردی و معادله درجه دو و حل آن — به زبان ساده نیز خالی از لطف نیست.
حل معادله در اکسل
همانطور که میدانید، اکسل یک ابزار محاسباتی است. بنابراین برای حل یک معادله میتوان از آن استفاده کرد. به این ترتیب، برای معادلاتی که به صورت پارامتری در اکسل تعریف میکنیم از سه شیوه برای پیدا کردن ریشه استفاده خواهیم کرد. در بخش اول، براساس فرمولنویسی معادلات را حل کرده و سپس از ابزارهای اکسل برای حل معادله در اکسل استفاده خواهیم کرد. ولی قبل از هر چیز باید بدانیم که یک معادله چیست؟
یک معادله به صورت یک تساوی (برابری) نوشته میشود که در دو طرف این تساوی، متغیر به همراه ضریب و مقادیر ثابت قرار میگیرند. در زیر نمونه یک معادله درجه ۱ (خطی) را مشاهده میکنید که به شکل استاندارد نوشته شده است.
منظور از حل این معادله، پیدا کردن مقدار یا مقادیری از است که طرف چپ را به صفر تبدیل کنند. به این ترتیب دو طرف با یکدیگر معادل (برابر) خواهند شد. به چنین مقداری از ، «ریشه معادله» (Equation Root) نیز گفته میشود. واضح است که ریشه این معادله برابر با است.
یک معادله خطی به صورت کلی و استاندارد را به شکل زیر نشان میدهند. در این حالت را ضریب و را مقدار ثابت مینامند.
ریشه چنین معادلهای به صورت زیر بدست خواهد آمد.
رابطه ۱: ریشه معادله مرتبه یک
از طرفی برای معادله درجه ۲ نیز فرم استاندارد زیر را خواهیم داشت.
که در این حالت با توجه به وضعیت و علامت نسبت به تعداد ریشههای حقیقی و نحوه محاسبه آنها تصمیم میگیریم.
رابطه ۲: ریشههای معادله درجه ۲
در صورتی که منفی باشد، هیچ ریشه با مقادیر حقیقی وجود ندارد. براساس محاسبات میتوان نشان داد که معادله زیر دارای دو ریشه است. واضح است که است.
نکته: در صورتی که دلتا () منفی باشد، باز هم دو ریشه موجود است ولی آنها متعلق به مجموعه اعداد مختلط هستند.
در ادامه به بررسی ریشهیابی این دو گونه معادله خواهیم پرداخت. ابتدا روش پیدا کردن ریشه معادله درجه اول و دوم را به کمک فرمولنویسی معرفی کرده، سپس به کمک ابزار Goal Seek حل معادل در اکسل را برای این دو نوع معادله مشخص میکنیم و در انتها نیز با استفاده از افزونه Solver، ریشههای معادلات درجه اول و دوم را بدست خواهیم آورد.
حل معادله در اکسل به کمک فرمول نویسی
برای آنکه بتوانیم یک معادله خطی (مرتبه اول) را حل کنیم، باید مسئله را به درستی در اکسل وارد کنیم. فرض کنید ریشه معادله خطی زیر مورد نظر است.
چنین معادلهای را باید ابتدا به صورتی در سلولها معرفی کنیم. پارامتری بودن رابطه بالا به ما این کمک را میکند که با وارد کردن مقادیر مختلف برای و و همچنین فرمول ریشه این معادله، بتوانیم پاسخ را به سادگی دریافت کنیم.
در تصویر زیر، یک کاربرگ با مقادیر را مشاهده میکنید.
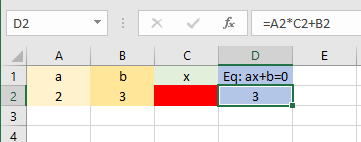
هدف پیدا کردن مقداری از است که اگر در سلول C2 نوشته شود، مقدار سلول D2 را صفر میکند. یک راه حل میتواند مقدار دهی و سعی و خطا باشد. البته این روش، بسیار وقتگیر بوده و ممکن است در زمان کوتاه به پاسخ صحیح نیز نرسیم. ولی اگر در سلول C2 فرمول کلی حل معادله خطی را وارد کنیم، به سادگی حل معادله در اکسل بدست خواهد آمد. بنابراین فرمول زیر را در سلول C2 براساس رابطه ۲ وارد میکنیم.
به این ترتیب مقدار C2 برابر با ۱٫۵- خواهد بود. تصویر ۲، نتیجه محاسبات ریشه و همچنین مقدار معادله را نشان میدهد. همانطور که مشخص است، مقدار عبارت که در سلول D2 نوشته شده به ازاء برابر با صفر خواهد بود.
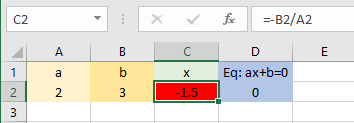
نکته: از آنجایی که فرمولهای نوشته شده، سلولهای وابسته ایجاد کردهاند، با تغییر مقادیر a و b، معادله جدید ساخته شده و محاسبات صورت میگیرد. به این ترتیب میتوانید هر معادله درجه یک را بوسیله این کاربرگ حل و ریشهها را پیدا کنید.
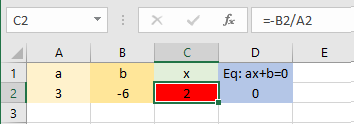
به عنوان یک مثال دیگر برای حل معادله در اکسل رابطه زیر را به صورت یک تساوی (Equation) در نظر میگیریم. واضح است که مقدار است.
تصویر ۳، نتیجه محاسبه و حل معادله و پیدا کردن ریشه را نمایش میدهد.
برای حل معادله در اکسل با مرتبه ۲، ابتدا مسئله را معرفی کرده و پارامترهای آن را به عنوان سلولها مشخص میکنیم. در تصویر ۴، چنین کاری صورت گرفته است.
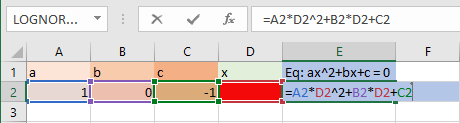
حال کافی است که ریشهها را به ترتیب برای در سلولهای D2 , D3 مشخص کنیم. برای این کار از رابطه ۲ استفاده کرده و محاسبات را صورت میدهیم. در تصویر ۵، این کار انجام شده و ریشههای معادله درجه ۲ زیر بدست آمده است. همانطور که انتظار داشتیم، ریشهها برابر با ۱ و ۱- هستند.
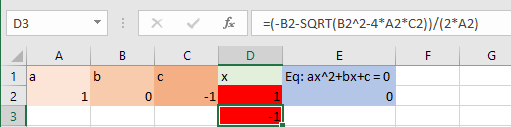
این بار معادلهای به صورت زیر را در نظر بگیرید. کافی است مقادیر مربوط به پارامترها را که در سلولهای A2 تا C2 وجود دارند را مقدار دهی کرده تا ریشههای معادله بدست آیند.
ریشهها برابر با 0٫۵- و ۲- خواهند بود. به تصویر ۶ توجه کنید. مشخص است که است.
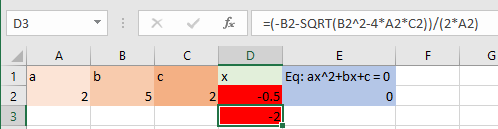
واضح است که ریشهها را به کمک فرمول زیر بدست آوردهایم. به پرانتزها و محل قرارگیر آنها توجه کنید.
= (-B2 +SQRT(B2^2 -4*A2 *C2)) / (2*A2)
ریشه دوم نیز به شکل زیر است.
= (-B2 - SQRT(B2^2- 4*A2*C2)) / (2*A2)
حل معادله در اکسل با ابزار Goal Seek
یکی از ابزارهای مناسب برای پیدا کردن مقدار تابع هدف در حالت تک متغیره، Goal Seek است. به کمک Goal Seek با عمل سعی و خطا، اکسل سعی در پیدا کردن مقدار تعیین شده برای یک فرمول (سلول وابسته) میکند. به این ترتیب با تعیین آدرس سلول پیشنیاز برای Goal Seek، اکسل مقادیر مختلف (از بزرگترین تا کوچکترین مقدار) را برای آن سلول در نظر گرفته تا سلول وابسته به مقداری که کاربر تعیین کرده، برسد. البته حدس اولیه (مقدار جاری برای سلول پیشنیاز) در سرعت بخشیدن به اجرای عملیات موثر است.
البته همیشه این امکان وجود ندارد و ممکن است که مقدار دهی باعث همگرایی در پاسخ نباشد. در این هنگام Goal Seek با پیغام خطا مواجه شده و به کاربر اعلام میدارد که به پاسخ مناسب نرسیده است.
مسیر دسترسی به این ابزار اکسل، از طریق برگه Data و گزینه What-If-Analysis از بخش Forecast است. در تصویر ۷، پنجره Goal Seek و تنظیمهای آن را برای پیدا کردن ریشه معادله زیر مشاهده میکنید.
همانطور که میبینید، سه پارامتر یا گزینه در این پنجره وجود دارد.
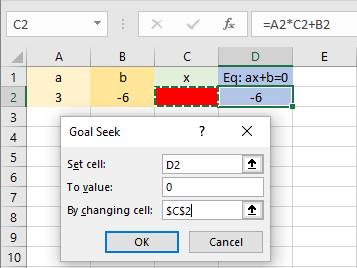
پارامتر Set cell، به آدرس سلولی اشاره دارد که به عنوان سلول وابسته به کار رفته و مقدار معادله را نشان میدهد. بخش To value نیز مقدار مورد نظر برای سلول وابسته را مشخص میکند. از آنجایی که ریشه معادله مد نظر است، مقدار سلول وابسته باید صفر شود. بنابراین این پارامتر را ۰ در نظر گرفتهایم. آخرین گزینه و مهمترین بخش در Goal Seek، By changing cell است. این گزینه مربوط به سلولی است که به عنوان پیشنیاز برای سلول وابسته شناخته شده و قرار است ریشه را نشان دهد.
همانطور که در بحث مربوط به ریشه معادله بیان شد، مقداری که باعث شود دو طرفه معادله با یکدیگر مساوی شوند، ریشه یا پاسخ معادله است. از آنجایی که یک طرف این معادله صفر است، طرف دیگر نیز باید صفر شود. بنابراین با تعیین مقادیر مختلف برای سلول C2 اکسل سعی میکند مقدار D2 را برابر صفر بدست آورد.
با فشردن دکمه OK، عملیات مقدار دهی صورت گرفته و در صورت همگرایی به پاسخ، پنجرهای مانند زیر ظاهر میشود. وجود پاسخ توسط اکسل با عبارت found a solution مشخص شده است.
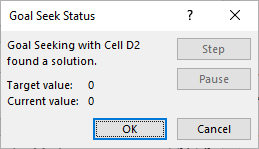
همانطور که در تصویر ۸ دیده میشود، مقدار هدف (Target value) صفر بوده و مقدار جاری (Current value) نیز صفر است. بنابراین به پاسخ رسیدهایم. مقدار پاسخ در سلول پیشنیاز نمایش داده شده (C2) و صفر بودن سلول وابسته (D2) نیز موید بدست آوردن ریشه معادله است.
نکته: به یاد داشته باشید که برای استفاده از Goal Seek همواره باید یک سلول وابسته و پیشنیاز وجود داشته باشد در غیر اینصورت امکان پیدا کردن مقدار هدف برای یک فرمول وجود ندارد.
در گام بعدی به سراغ معادله درجه ۲ خواهیم رفت و سعی میکنیم که بوسیله این تکنیک، ریشه (ریشههای) معادله زیر را پیدا کنیم.
ابتدا ریشه اول را بدست خواهیم آورد. تنظیمهای Goal Seek را طبق تصویر 9 انجام میدهیم. باز هم میبینید که از همان پارامترها یعنی آدرس سلول وابسته، مقدار هدف برای سلول وابسته و آدرس سلول پیشنیاز استفاده کردهایم.
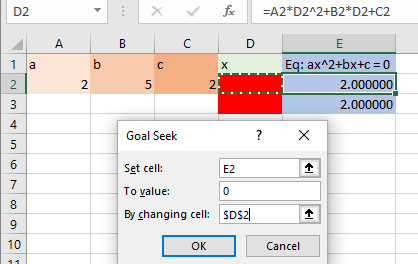
پس از فشردن دکمه OK اولین ریشه به این ترتیب حاصل میشود. مشخص است که مقدار ریشه باید برابر با ۰٫۵- یا نزدیک به آن باشد.
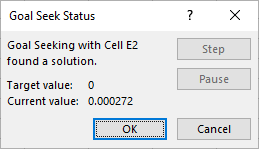
در تصویر 10 مشاهده میکنید که مقدار مورد انتظار برای معادله برابر با صفر است ولی نتیجه تقریبا با صفر برابر (0٫000272) است. بنابراین ریشه مقداری تقریبی است. از طرفی مقدار ریشه نیز در سلول D2 حاصل شده که ۰٫۴۹۹۹- را نشان میدهد که باز هم تقریبا با ۰٫۵- برابر است.
برای پیدا کردن ریشه دوم، کمی اکسل را کمک میکنیم. به این معنی که حدس اولیه برای ریشه دوم را در سلول D3 مینویسیم. اکسل همیشه از مقداری که در سلول پیشنیاز معرفی شده به عنوان نقطه شروع استفاده میکند. میدانیم که ریشه دوم برابر با ۲- است. پس برای مثال مقدار سلول پیشنیاز را مثلا ۳- قرار میدهیم. سپس با استفاده از Goal Seek به جستجو ریشه میپردازیم. این بار اکسل باز هم به صورت تقریبی به ریشه دست پیدا میکند.
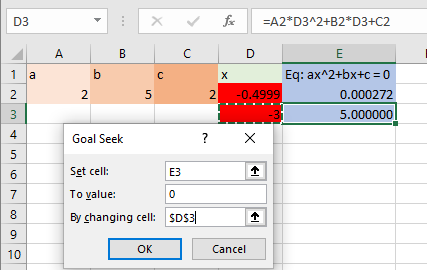
نتیجه برای سلول وابسته مقدار 0٫000765 (نزدیک به صفر) و مقدار ریشه ۲٫00025- (نزدیک به ۲) است.
نکته: توجه داشته باشید که دو بار فرمول مربوط به معادله درجه ۲ را نوشتهایم. یکبار در سلول E2 (برای پیدا کردن ریشه اول) و یکبار هم در سلول E3 (برای پیدا کردن ریشه دوم). بنابراین یکبار سلول D2 و یکبار هم سلول D3 را پیشنیاز قرار دادهایم.
حل معادله در اکسل با افزونه Solver
بسیاری از محاسبات و عملیات پیچیده در اکسل بوسیله توابع یا ابزارهای آن، به سادگی قابل اجرا است. یکی از این ابزارهای مفید، Solver است که یک افزونه (Add-ins) محسوب میشود. افزونه Solver، قادر است برای یک تابع هدف، به ازاء محدودیتهای مختلف (Constrain)، جواب بهینه را مشخص کند. به عنوان یک تکنیک بهینه سازی میتوان در Solver از روش سیمپلکس (Simplex) یا GRG و همچنین «الگوریتمهای تکاملی» (Evolutionary Engine) نیز کمک گرفت.
در این بخش نیز سعی داریم به کمک چندین مثال، از Solver استفاده کرده و معادلات درجه یک و دو را حل و ریشه یا ریشهها را پیدا کنیم. قبل از هر چیز مراحل اضافه کردن این افزونه را در اکسل بازگو کرده، سپس نحوه استفاده از آن برای ریشهیابی را مشخص خواهیم کرد.
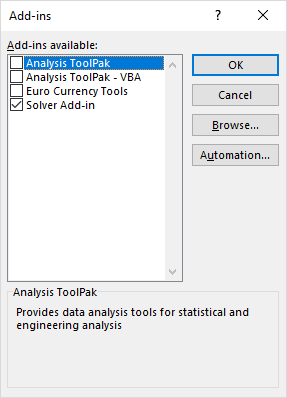
به منظور نصب و راهاندازی Solver، از فهرست File گزینه Options و قسمت Add-ins را انتخاب و از کادر سمت راست در قسمت Manage گزینه Excel Add-ins را انتخاب کرده و دکمه …Go را کلیک کنید. سپس در پنجره Add-ins گزینه Solver را انتخاب و دکمه OK را بزنید.
به این ترتیب، افزونه Solver را در برگه Data و در قسمت Analyze مشاهده خواهید کرد. با کلیک کردن روی آن به پنجره Solver دسترسی خواهید داشت.
حل معادله خطی مرتبه یک در اکسل با Solver
این بار هم فرض کنید که قرار است معادله زیر را حل کرده و ریشه را بدست آوریم. مشخص است که این معادله خطی بوده و از درجه یک است.
پنجره Solver را باز کرده و تنظیمها را مطابق با تصویر 13 اجرا خواهیم کرد.
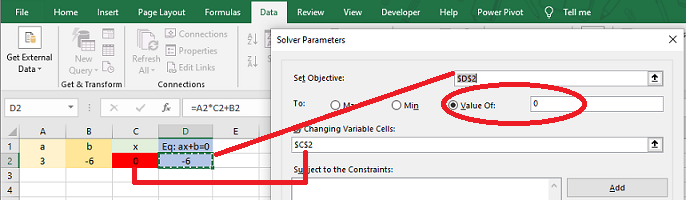
مشخص است که بخش Set Objective، به سلولی اشاره میکند که تابع هدف (معادله) در آن نوشته شده به همین علت آدرس سلول D2 را برای آن انتخاب کردهایم. از طرفی قرار است مقدار این فرمول به صفر برسد زیرا به ریشههای آن احتیاج داریم. بنابراین در قسمت TO گزینه Value of را صفر در نظر میگیریم. از طرفی مقداری که ریشه را نشان میدهد در سلول C2 قرار گرفته است. در نتیجه با معرفی آن در بخش By changing variable cells تعیین پارامترهای ابزار Solver تکمیل میشود.
پس از فشردن دکمه OK، افزونه Solver محاسبات را انجام داده و نتیجه را نشان میدهد. به تصویر 14 توجه کنید.
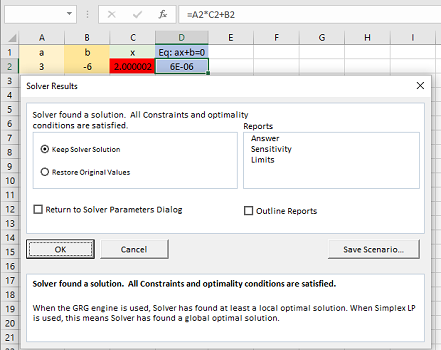
همانطور که مشاهده میکنید، اعلام شده است که Solver به کمک متد یا روش GRG Nonlinear به نتیجه رسیده است. در سلول C2 مقدار ریشه (۲٫۰۰۰۰۰۰۲) و در سلول D2 نیز مقدار تابع هدف () را میبینید که به صفر بسیار نزدیک است. واضح است که این مقدار به صورت نماد علمی نمایش داده شده.
نکته: از آنجایی که معادله خطی است و از روش غیرخطی GRG استفاده شده، نتیجه تقریبی حاصل شده است. عبارت GRG مخفف Generalized Reduced Gradient به معنی «گرادیان کاهشی تعمیم یافته» است. به این ترتیب با مشتقگیری و تغییر مقادیر، به جواب بهینه خواهیم رسید.
گزینههای این پنجره به صورت زیر هستند.
- Keep Solver Solution: با انتخاب این گزینه که به طور پیشفرض نیز فعال است، نتیجه حاصل از اجرای Solver در سلولها باقی میماند.
- Restore Original Values: این گزینه مقادیر قبلی سلولها را به قبل از اجرای Solver باز میگرداند.
- Reports: این بخش به منظور بررسی نتایج حل مسائل «برنامهریزی خطی» (Linear Programming) اختصاص داشته و تحلیل حساسیت و کرانهای پاسخ را مشخص میکند.
- Return to Solver Parameters Dialog: بازگشت به پنجره تعیین پارامترهای Solver را پس از فشردن کلید OK موجب میشود.
- Outlier Reports: نقاط پرت یا «دورافتاده» (Outlier) را در گزارش نهایی ارائه میکند. البته این مورد برای برازش خط مفید است.
دکمه Save Scenario نیز باعث میشود، نتایج Solver به همراه مقادیر قبل از اجرای Solver تحت سناریوهای مختلف ذخیره شود.
این بار محاسبات برای حل این معادله خطی را به کمک روش Simplex LP یا سیمپلکس برنامه ریزی خطی (Simplex Linear Programming) ارائه میکنیم. تنظیمها را به مانند قبل در پنجره Solver اجرا کرده ولی در قسمت Select a Solving Method گزینه Simplex LP را انتخاب میکنیم.
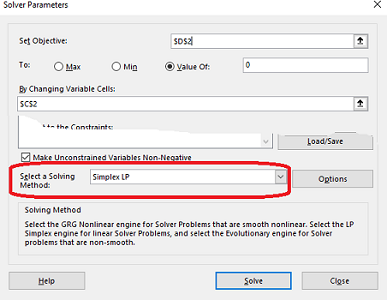
با این کار جواب دقیق برای معادله حاصل شده و در سلول D2 مقدار ۲ و در سلول E2 مقدار صفر را مشاهده میکنید. در بخش توضیحات که در کادر پایین پنحره تصویر 16 دیده میشود، مشخص شده است که پاسخ (ریشه) پیدا شده و همه قیدهای مربوط به بهینهسازی حاصل شدهاند. البته مشخص است که برای بدست آوردن ریشه معادله خطی، هیچ قیدی در نظر گرفته نشده بود.
حل معادله غیرخطی در اکسل با Solver
در این بخش باز هم به معادله درجه ۲ میپردازیم و ریشههای آن را به کمک Solver مشخص میکنیم. البته از آنجایی که تکنیک Simplex LP، برای معادلات خطی مناسب است، ممکن است هنگام استفاده از آن برای پیدا کردن ریشه معادلات غیر خطی (مانند معادله درجه ۲) به مشکل برخورد کرده و به جواب مناسب نرسیم. به همین دلیل از گزینه GRG Nonlinear برای پیدا کردن ریشهها استفاده خواهیم کرد. معادله زیر را در نظر بگیرید.
باز هم برای مشخص کردن این معادله در کاربرگ اکسل به مانند تصویر 11 استفاده کرده و پارامترهای معادله خطی را به صورت مقادیر درون سلولها نمایش میدهیم. در تصویر 17، تنظیمهایی که برای معرفی و حل معادله در اکسل با Solver لازم داریم را نمایش دادهایم.
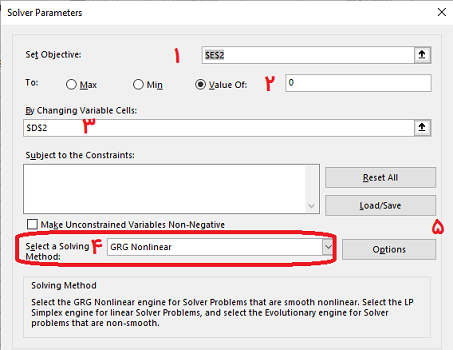
همانطور که در این تصویر مشاهده میکنید، برای حل معادله در اکسل به کمک Solver، پارامترها و ترتیب تعیین آنها با شماره مشخص شدهاند. در زمانی که گزینه GRG Nonlinear را انتخاب کردید با فشردن دکمه Options، به پنجره تنظیمهای تکنیکهای قابل استفاده در Solver دست پیدا میکنید. در تصویر 18 پنجره مناسب برای پارامترهای عمومی و در تصویر 19 پارامترهای مناسب برای روش GRG را مشاهده میکنید.
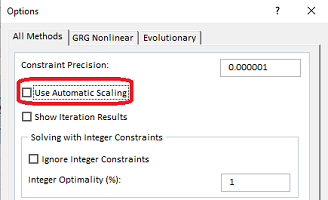
در تصویر ۱۷ میبینید که گزینه مقیاسبندی خودکار (Use Automatic Scaling) را غیر فعال کردهایم. اگر میخواهید نتایج حاصل از جایگذاری و مقدار دهی را در روش GRG مشاهده کنید، گزینه Show Iteration Results را فعال کنید.
نکته: از آنجایی که دو ریشه وجود دارد، تنظیم گزینههای مربوط به تصویر ۱۷ و ۱۸ ضروری است. در غیر این صورت ممکن است Solver به جواب بهینه نرسد.
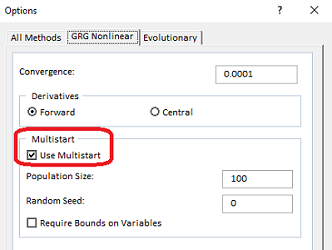
در تصویر 19 گزینه User Multistart را انتخاب کردهایم تا بوسیله آن از چند نقطه به عنوان نقطه آغازین استفاده شود. این کار سرعت رسیدن به پاسخ را افزایش میدهد. از طرفی فعال سازی روش مشتقگیری پیشرو (Forward) و مرکزی (Center) نیز در افزایش کارایی روش GRG موثر است. مقدار «دانه تصادفی» (Random Seed) نیز اختیاری است.
با توجه به اینکه معادله درجه ۲، حداکثر دو ریشه دارد، برای حل معادله در اکسل باید دوبار از Solver استفاده کرده و با پارامترهای یکسان دو جواب برای معادله را بدست آورد. واضح است که معادله دارای ریشههایی برابر با ۲- و ۰٬۵- است. ولی نتیجه به وسیله تکنیک GRG ریشههایی برابر با 1٫999997- و ۰٫۵- را ارائه کرده است. این مقادیر را در تصویر 20 مشاهده میکنید.
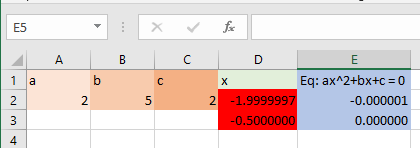
مشخص است که مقدار سمت چپ معادله نیز به صفر نزدیک شده ولی برابر با نیست. اگر گزینه Answer را در بخش Report (مانند تصویر 16) انتخاب میکردید، گزارشی از مراحل کار و نتایج حاصل شده توسط GRG در یک کاربرگ جدید ظاهر میشد. در تصویر 21 نمونهای از این گزارش را مشاهده میکنید.
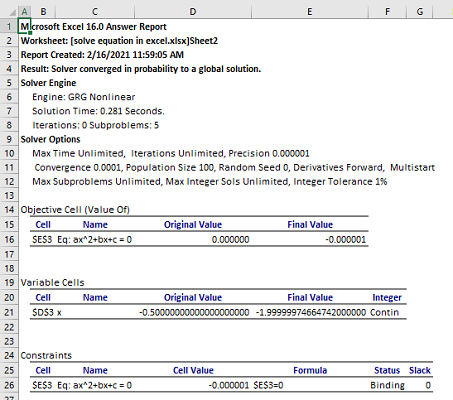
در تصویر 21، تابع هدف (Objective Cell) و همچنین سلولهای پیشنیاز (Variable Cells) به همراه مقادیر اولیه (Original Value) و پاسخ نهایی (Final Value) مشخص شدهاند. مطالعه این گزارش، شما را از زمان اجرای الگوریتم (Solution Time) و همچنین تعداد تکرار (Iterations) آگاه میسازد.
همانطور که دیدید حل معادله در اکسل و تکنیکهای آن متعدد و متنوع است. به منظور راحتی و سادگی کار حل معادله در اکسل کارپوشه مربوط به حل معادله درجه یک و دو را که در این متن به آن اشاره کردیم، در اختیارتان قرار دادهایم. کافی است آن را با قالب فشرده از اینجا دریافت کرده، پس از خارج کردن از فشردگی در اکسل بارگذاری کنید. به این ترتیب با تعیین پارامترهای معادلات، پاسخها یا ریشهها را پیدا و حل معادله در اکسل را به راحتی اجرا میکنید.
خلاصه و جمعبندی
همانطور که دیدید، برای پیدا کردن ریشههای یک معادله، روشهای مختلفی در اکسل وجود دارد. حل معادله در اکسل را به کمک فرمول نویسی میتوان اجرا کرد. همچنین استفاده از ابزارهای داخلی مانند Solver و Goal Seek نیز تکنیکهای حل معادله در اکسل محسوب میشوند. در این متن از هر سه مورد استفاده کرده و با ذکر مثالهایی، نحوه کار را یادآوری کردیم.












با سلام
برای حل معادلات درجه سوم و بالاتر میشه از این روش استفاده کرد ؟
با تشکر
با سلام و عرض ادب
توضیحات بسیار عالی بود و بی نظیر
سپاس بیکران
سلام و عرض ادب
وقت بخیر
هدفم نوشتن فرمولی هست که معادلهای را با شرایط مثال زیر حل کند:
(10) * 4 = (2) * 6 + (4) * 7
اعداد خارج پرانتز ورودی هستند و اعداد داخل پرانتز نتیجه خروجی. نکته اول اینکه خروجیها لزوما باید زوج باشند و نکته دوم اینکه اگر به هر ترتیب امکان حاصل شدن خروجی به صورت دقیق نبود، حالتی که کمترین اختلاف با عدد زوج صحیح کوچکتر از خودش رو داره، به صورت صحیح برای نتایج خروجی ارائه شود. برای مثال
(8) * 2.3 = (2) * 2 + (8) * 1.2
8*2.3=18.4
2*2=4
18.4 – 4 =14.4
14.4 / 1.2 = 8.16 ~ 8
این نتایج رو خودم هر بار با سعی و خطا و در نظر گرفتن حالات مختلف به دست میارم، خواستم ببینم امکانی نیست که دقت و سرعتم بالا بره چون در مواردی واقعا این روند وقتگیر هست.
ممنون میشم اگر محبت کنید و کمکم کنید
سلام دوست و خواننده گرامی،
در فایلی که طبق این لینک قابل دریافت است، سعی کردم به کمک Solver مسئله شما را حل کنم ولی متاسفانه به دلیل محدودیتهایی که اکسل برای حدس اولیه دارد، قادر به پیدا کردن پاسخ مناسب نشد. توجه داشته باشید که زوج بودن پاسخها را به کمک تابع MOD و محاسبه باقی مانده تقسیم عدد بر ۲ مشخص کرده ام.
پیروز و پایدار باشید.