حل معادله درجه ۲ در متلب | گام به گام (+ دانلود نمونه کد)

در این نوشتار حل معادله درجه 2 در متلب را آموزش می‌دهیم و با ارائه مثال و نمونه کد در این زمینه در متلب سعی خواهیم داشت درک این آموزش را ساده‌تر و ملموس‌تر کنیم. اگر حل معادله درجه 2 در متلب برای شما نیز دشوار است خواندن این مطلب و این آموزش را از دست ندهید.

معادله دیفرانسیل درجه 2

همان طور که در مطالب قبلی توضیح دادیم منظور از درجه یک معادله دیفرانسیل بالاترین درجه مشتق در معادله است. بدین ترتیب منظور از معادله درجه 2 معادله‌ای است که بالاترین درجه مشتق در آن دو باشد. شکل کلی یک معادله دیفرانسیل درجه 2 را به صورت زیر می‌توان معرفی کرد:

$$\frac{d^{2}y}{dx^{2}}+P(x)\frac{dy}{dx}+Q(x)y=f(x)$$

فیلم آموزش برنامه نویسی متلب برای علوم و مهندسی در فرادرس

کلیک کنید

در تعریف بالا اگر $$f(x)$$ برابر با صفر باشد یک معادله همگن داریم و اگر غیر صفر باشد معادله غیرهمگن است. برای حل یک معادله دیفرانسیل درجه 2 اگر P و Q ثابت باشند، با توجه به مقدار $$P^2-4Q$$ سه حالت مختلف وجود دارد:

• اگر $$P^2-4Q$$ مثبت باشد، 2 ریشه حقیقی به صورت $$r_1$$ و $$r_2$$ وجود دارد و جواب به صورت زیر است:

$$y=Ae^{r_1x}+Be^{r_2x}$$

• اگر $$P^2-4Q$$ صفر باشد، 1 ریشه حقیقی به صورت $$r$$ وجود دارد و جواب به صورت زیر است:

$$y=Ae^{rx}+Bxe^{rx}$$

• اگر $$P^2-4Q$$ منفی باشد، 2 ریشه مختلط به صورت $$r_1=v+wi$$ و $$r_2=v-wi$$ وجود دارد و جواب به صورت زیر است:

$$y=e^{vw}(C\cos(wx)+iD\sin(wx))$$

با این مقدمه به آموزش حل معادله درجه 2 در متلب می‌پردازیم.

تعریف تابع در متلب

توابع را در متلب در ‎.m فایل می‌سازیم. جزئیات تعریف تابع در متلب را در مطلب حل دستگاه معادلات دیفرانسیل غیر خطی در متلب توضیح دادیم در این قسمت تعریف یک تابع در متلب را با روش‌های مختلف بررسی می‌کنیم.

فیلم آموزش برنامه نویسی متلب MATLAB در فرادرس

کلیک کنید

تعریف تابع در متلب با یک خروجی

می‌خواهیم تابعی به نام average.m تعریف کنیم که به عنوان ورودی یک بردار قبول می‌کند. توسط تابع average میانگین بردار محاسبه شده و در خروجی میانگین چاپ می‌شود. برای این کار تابع را در فایل اسکریپت به صورت زیر تعریف می‌کنیم:

1function ave = average(x)
2    ave = sum(x(:))/numel(x); 
3end

این فایل را در سیستم خود با نام خود تابع یعنی average.m ذخیره کرده و در صفحه Command بازه متغیر را معرفی می‌کنیم و با فراخوانی نام تابع میانگین بردار در خروجی نمایش داده می‌شود:

1z = 1:99;
2ave = average(z)

دقت کنید که اگر در خروجی با پیغام خطای زیر رو به رو شدید:

Undefined function or variable 'average'‎

باید از طریق نواری که در تصویر (1) نشان داده شده است فولدر متلب را به مکانی که در آن تابع را ذخیره کرده‌اید تغییر دهید.

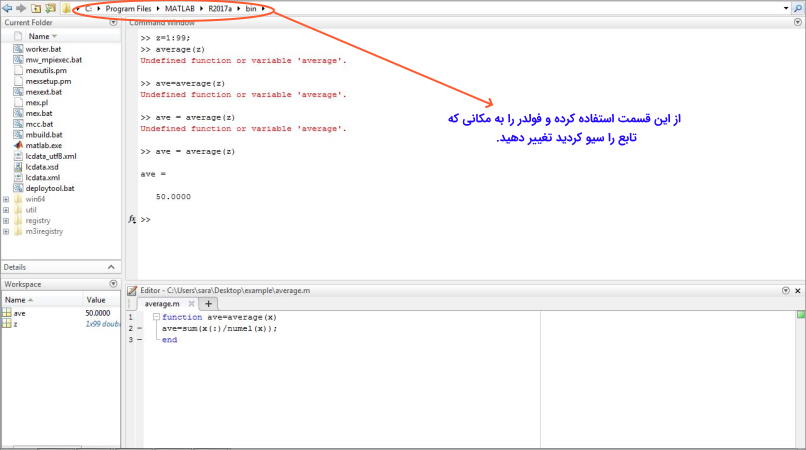
تعریف تابع در متلب با چند خروجی

در این قسمت می‌خواهیم تابعی با نام stat تعریف کنیم که یک بردار x را به عنوان ورودی دریافت کند و خروجی m و s را که برابر با میانگین بردار x و مجموع انحراف از میانگین هر یک از داده‌های x است را در خروجی چاپ کند. بدین ترتیب برای تعریف این تابع به صورت زیر عمل می‌کنیم:

1function [m,s] = stat(x)
2    n = length(x);
3    m = sum(x)/n;
4    s = sqrt(sum((x-m).^2/n));
5end

حال مقادیر بردار x را تحت عنوان values به صورت زیر تعریف کرده و تابع stat را فراخوانی می‌کنیم.

1values = [12.7, 45.4, 98.9, 26.6, 53.1];
2[ave,stdev] = stat(values)

در نهایت خروجی‌ها یعنی میانگین و انحراف از میانگین values چاپ می‌شوند.

تعریف تابع در فایل اسکریپت متلب

در یک فایل اسکریپت متلب می‌خواهیم تابعی با نام integrationScript.m را تعریف کنیم که مقدار تابع را در $$2\pi/3$$ مشخص کند و سطح زیر نمودار را در بازه $$0$$ تا $$\pi$$ محاسبه کند. در فایل اسکریپت نیز به همان ترتیب توضیح داده شده عمل می‌کنیم و داریم:

1% Compute the value of the integrand at 2*pi/3.
2x = 2*pi/3;
3y = myIntegrand(x)
4
5% Compute the area under the curve from 0 to pi.
6xmin = 0;
7xmax = pi;
8f = @myIntegrand;
9a = integral(f,xmin,xmax)
10
11function y = myIntegrand(x)
12    y = sin(x).^3;
13end

در این حالت با اجرای فایل اسکریپت برای تابع $$\sin^{3}(x)$$ مقدار تابع در $$2\pi/3$$ و سطح زیر تابع بین $$0$$ تا $$\pi$$ در خروجی چاپ می‌شود.

در این مثال دقت کنید که نام فایل همانند مثال‌های قبلی نام تابع نیست و اگر فایل را به نام تابع ذخیره کنید با پیغام خطا رو به رو می‌شوید.

تعریف چند تابع در یک اسکریپت فایل متلب

در این حالت دو تابع را در یک اسکریپت تعریف می‌کنیم که در تابع اول تابع دوم را فراخوانی کرده و داریم:

1function [m,s] = stat2(x)
2    n = length(x);
3    m = avg(x,n);
4    s = sqrt(sum((x-m).^2/n));
5end
6
7function m = avg(x,n)
8    m = sum(x)/n;
9end

با تعریف برداری مانند values و فراخوانی تابع stat2 خروجی‌ها در صفحه Command نمایش داده می‌شوند.

تعریف یک تابع با محدود کردن نوع آرگومان در متلب

می‌خواهیم برای مثال‌های بالا روی ورودی‌های تابع محدودیت اعمال کنیم. برای مثال برای محاسبه میانگین و انحراف از میانگین بردار x می‌خواهیم این محدودیت را اعمال کنیم که مقادیر عددی باشند و بی‌نهایت نباشند. بدین منظور به صورت زیر عمل می‌کنیم:

1function [m,s] = stat3(x)
2    arguments
3        x (1,:) {mustBeNumeric, mustBeFinite}
4    end
5    n = length(x);
6    m = avg(x,n);
7    s = sqrt(sum((x-m).^2/n));
8end
9
10function m = avg(x,n)
11    m = sum(x)/n;
12end

حالا با تعریف ورودی‌ها به صورت زیر:

1values = [12.7, 45.4, 98.9, NaN, 53.1];

و با فراخوانی تابع stat3 برای مقادیر بردار values این پیغام را مشاهده خواهید کرد:

1Invalid input argument at position 1. Value must be finite.

حل پارامتری معادله درجه 2 در متلب با دستور dsolve

بعد از توضیح در مورد معادله درجه 2 و روش‌های متفاوت تعریف یک تابع در متلب در این قسمت حل یک معادله درجه 2 در متلب را به صورت پارامتری بررسی می‌کنیم. بدین منظور تابعی را در نظر بگیرید که دارای شرایط اولیه تعریف شده به صورت زیر است:

$$\frac{d^2y}{dx^2}=\cos(2x)-y$$
$$\begin{cases}y(0)=1 \\y^{\prime}(0)=0\end{cases}$$

فیلم آموزش روش های عددی ریشه یابی و حل معادلات و پیاده سازی در متلب MATLAB در فرادرس

کلیک کنید

1syms y(x)
2Dy = diff(y);
3
4ode = diff(y,x,2) == cos(2*x)-y;
5cond1 = y(0) == 1;
6cond2 = Dy(0) == 0;
7
8conds = [cond1 cond2];
9ySol(x) = dsolve(ode,conds);
10ySol = simplify(ySol)

در این روش از دستور dsolve برای حل معادله درجه 2 در متلب استفاده کردیم، همچنین شرایط اولیه را نیز تحت عنوان conds در دستور dsolve  وارد کردیم. در خط آخر اگر دستور simplify را وارد نکنید، جواب به صورت زیر نمایش داده می‌شود:

1ySol(x) =
2 
3(5*cos(x))/3 + sin(x)*(sin(3*x)/6 + sin(x)/2) - (2*cos(x)*(6*tan(x/2)^2 - 3*tan(x/2)^4 + 1))/(3*(tan(x/2)^2 + 1)^3)

با وارد کردن دستور simplify جواب به صورت ساده شده و به صورت زیر در خروجی نمایش داده می‌شود:

1ySol(x) =
2 
31 - (8*sin(x/2)^4)/3

حل عددی معادله درجه 2 در متلب با دستور ode45

در این بخش می‌خواهیم یک معادله درجه 2 در متلب را با استفاده از دستور ode45 حل کنیم. برای این منظور تابعی را مانند زیر در نظر می‌گیریم:

$$y^{\prime\prime}=2y+8x(9-x)$$

فیلم آموزش محاسبات انتگرال با متلب و میپل MATLAB و Maple در فرادرس

کلیک کنید

که شرایط اولیه برای تابع به صورت زیر تعریف شده است:

$$\begin{cases}y(0)=0\\y^{\prime}(0)=9\end{cases}$$

برای حل از روش تغییر متغیر استفاده می‌کنیم تا معادله به یک معادله درجه اول تبدیل شود و داریم:

1[x,y] = ode45(@fun,[0 -28],[0 9]);
2plot(x,y);grid on
3
4function dy = fun(x,y)
5dy = zeros(2,1);
6dy(1) = y(2);
7dy(2) = 2*y(1)+8*x*(9-x);
8end

با اجرای این کد تغییرات $$y$$ و $$y^{\prime}$$ در بازه $$-28$$ تا $$0$$ در نمودار نشان داده می‌شوند و همچنین تغییرات دو تابع نیز به عنوان خروجی نمایش داده می‌شوند. نمودار حاصل از اجرای کد به صورت زیر است:

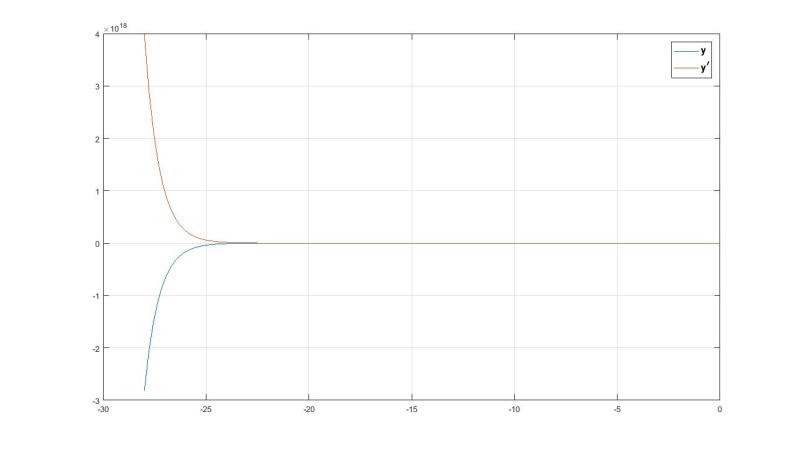
مثال‌های حل معادله درجه 2 در متلب

در این بخش مثال‌های دیگری از حل معادله درجه 2 در متلب را به روش عددی و پارامتری بررسی می‌کنیم. به عنوان مثال اول معادله زیر را با شرایط اولیه مشخص شده در نظر بگیرید:

$$2x^{2}\frac{d^2y}{dx^2}+3x\frac{dy}{dx}-y=0$$

می‌خواهیم این معادله را از طریق dsolve و بدون شرایط اولیه حل کنیم. کد متلب برای این مثال به صورت زیر خواهد بود:

1syms y(x)
2
3ode =  2*x^2*diff(y,x,2)+3*x*diff(y,x)-y == 0;
4ySol(x) = dsolve(ode)

با اجرای برنامه جواب به صورت کلی زیر به دست می‌آید:

$$\frac{C_1}{3x}+C_2x^{\frac{1}{2}}$$

که $$C_1$$ و $$C_2$$ ضرایب ثابتی هستند که با توجه به شرایط اولیه مسئله مقدار آن‌ها مشخص می‌شود. به عنوان آخرین مثال می‌خواهیم معادله زیر را به صورت عددی در متلب حل کنیم:

$$\frac{d^2y}{dt^2}=(1-y^2)\frac{dy}{dt}-y$$

برای حل این معادله از تغییر متغیر استفاده می‌کنیم تا درجه معادله را به مرتبه 1 تنزل دهیم. بدین منظور داریم:

$$\begin{cases}y(t)=Y_1\\ \frac{dY_1}{dt}=Y_2 \end{cases}$$

1syms y(t)
2[V] = odeToVectorField(diff(y, 2) == (1 - y^2)*diff(y) - y)

که در نهایت معادله به صورت زیر در می‌آید:

$$\begin{cases}\frac{dY_1}{dt}=Y_2\\ \frac{dY_2}{dt}=-(Y^2_1-1)Y_2-Y_1 \end{cases}$$

با استفاده از روش ode45 و استفاده از شرایط مرزی $$(2,0)$$ و حل عددی در بازه $$[0,20]$$ نتایج و مقادیر $$y$$ به صورت تصویر (3) به نمایش درمی‌آیند.

1syms y(t)
2[V] = odeToVectorField(diff(y, 2) == (1 - y^2)*diff(y) - y);
3M = matlabFunction(V,'vars', {'t','Y'})
4sol = ode45(M,[0 20],[2 0]);
5fplot(@(x)deval(sol,x,1), [0, 20])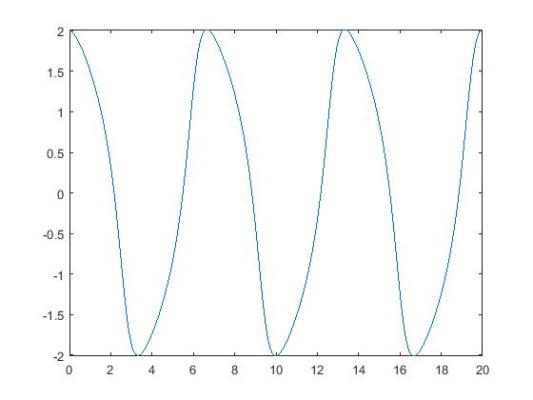

جمع‌بندی

این مطلب به حل معادله درجه 2 در متلب اختصاص داشت، بدین منظور در ابتدا نشان دادیم چگونه می‌توان در متلب معادلات را به روش‌های مختلف تعریف کرد. سپس به حل معادلات درجه 2 در متلب پرداختیم. این حل را از دو روش dsolve و ode45 انجام دادیم. می‌توان دید که در روش dsolve جواب به صورت پارامتری به دست می‌آید و در دستور ode45 جواب به صورت عددی و در بازه مشخص خواسته شده محاسبه می‌شود.