معادله منحنی در اکسل | به زبان ساده
دادههای عددی میتوانند اطلاعات زیادی را از یک پدیده به ما نشان بدهند. اغلب بوسیله مقادیر اندازهگیری شده از آزمایشهای فیزیکی یا شیمیایی، میخواهیم تابعی از متغیرهای محیطی بسازیم تا رفتار پدیده مورد نظرمان را به صورت یک رابطه ریاضی نشان دهد. به صورت کلی، به این کار «برازش منحنی» (Curve Fitting) میگویند که هدف آن پیدا کردن تابعی است که بیشترین توصیف از رفتار دادهها را ارائه یا نمایش دهد. ایجاد رابطه یا تابع خطی میتواند با تکنیک «رگرسیون خطی» (Linear Regression) صورت گیرد. ولی در این متن به شیوهای متفاوت توجه کرده که در آن براساس چند تابع معروف، سعی خواهیم کرد برآورد مناسبی برای پارامترهایی آنها ارائه دهیم. برای انجام این گونه محاسبات از صفحه گسترده اکسل کمک خواهیم گرفت. به این ترتیب با ابزارهای ترسیمی و محاسبات عددی، معادله منحنی در اکسل را مشخص کرده و رسم خواهیم کرد.
برای آشنایی بیشتر با توابع به کار رفته در این نوشتار، بهتر است مطالب برازش منحنی (Curve Fitting) — به زبان ساده و مهمترین الگوریتم های یادگیری ماشین (به همراه کدهای پایتون و R) — بخش دوم: رگرسیون خطی را بخوانید. همچنین مطالعه تقریب خطی — به زبان ساده و درون یابی خطی — به زبان ساده نیز خالی از لطف نیست.
معادله منحنی در اکسل
برازش منحنی یا تعیین معادله تابع در اکسل به سادگی صورت میگیرد. کافی است یک ستون برای متغیر مستقل (x) و یک ستون هم برای متغیر وابسته (y) در نظر بگیرید. به این ترتیب بین این دو ستون داده، تابعی به صورت زیر در نظر خواهیم گرفت.
$$ \large y = f(x) $$
انتخاب تابع $$f$$ کار مشکلی است بنابراین چند نوع تابع خاص که بیشتر برای پدیدههای طبیعی قابل استفاده هستند را در نظر گرفته و سعی میکنیم بهترین پارامترها را برای این توابع پیدا کنیم. معمولا برآورد پارامترهای چنین تابعی به کمک تکنیکهای «درونیابی» (Interpolation) صورت میگیرد. همچنین اگر لازم است که تخمینی برای نقطهای خارج از محدود دادههای موجود، صورت گیرد، «روشهای برونیابی» (Extrapolation) به کار میروند.
لیست توابعی که در تعیین معادله منحنی در اکسل قابل استفاده هستند، در جدول زیر دیده میشوند. پارامتر و خصوصیات این توابع نیز برای برازش روی دادهها در ستونهایی از این جدول قابل مشاهده است.
جدول ۱: نوع تابع و پارامترهای آن برای رسم معادله منحنی در اکسل
| نام تابع | فرمول | پارامترها | توضیحات |
| تابع نمایی - Exponential | $$y = c \; e^{bx} $$ | $$c ,\; b $$ | پارامترهای c و b ثابت بوده و e نیز عدد نپر است. |
| تابع خطی- Linear | $$y = m\;x + b $$ | $$ m ,\; b $$ | $$m$$ شیب و $$b$$ عرض از مبدا خط است. |
| تابع لگاریتمی - Logarithmic | $$y = c \ln (x) + b $$ | $$c ,\; b $$ | $$\ln$$ تابع لگاریتم طبیعی است. |
| تابع چند جملهای- Polynomial | $$y = b + c_x + c_2x^2 + \ldots + c_6 x^6 $$ | $$c_i ,\; b $$ | با تعیین مرتبه چند جملهای (Order) با مقدار حداکثر ۶ |
| تابع توانی- Power | $$ y = c x^b $$ | $$c ,\; b $$ | با تعیین دوره میانگینگیری (period) |
| تابع میانگین متحرک- Moving Average | $$F_t = \dfrac{A_t+A_{t-1} + \ldots+A_{t-n+1}}{n}$$ | $$t$$ | برای دادههای با ترتیب زمانی مناسب است. |
معمولا برآورد این پارامترها به شیوه محاسبات عددی و براساس مقادیر ثبت شده برای زوجهای $$(x,y)$$ صورت میگیرد. در تصویر ۱، این توابع را در قسمت «قالببندی منحنی روند» (Format Trendline) برای نمودارهای اکسل مشاهده میکنید.
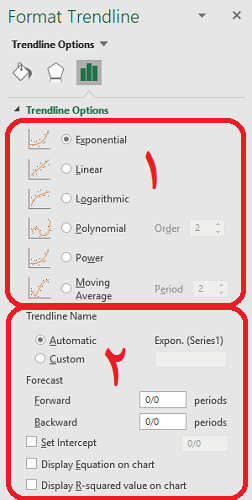
همانطور که در تصویر ۱ مشخص است، این قاب (Pane) دارای دو بخش است. بخش اول به تعیین نوع تابع پرداخته و بخش دوم نیز به تنظیمات مربوط به نحوه نمایش منحنی روند اختصاص دارد. به یاد داشته باشید که ابتدا باید یک نمودار با نوع مناسب داشته باشید تا بتوانید خط یا منحنی روند را روی آن ظاهر سازید. ایجاد منحنی روند برای دادههای ترسیم شده، در ادامه متن توضیح داده میشود. در جدول ۲ به معرفی گزینههای قابل انتخاب در بخش دوم این قاب خواهیم پرداخت.
| گزینه | عملکرد | توضیحات |
|
Trendline Name Automatic Custom | نام منحنی یا معادله
خودکار انتخابی | این نام در راهنمای نمودار ظاهر خواهد شد. |
|
Forecast Forward Backward | پیشبینی توسط خط روند
پیشرو پسرو | تعیین دوره بعدی و پیشین توسط periods تعیین میشود. |
|
Set Intercept | تعیین پارامتر عرض از مبدا | محل برخورد منحنی با محور عمودی را مشخص میکند. |
|
Display Equation on chart | نمایش معادله روی نمودار | |
|
Display R-squared value in chart | نمایش ضریب تعیین روی نمودار | مقداری بین صفر تا یک برای نمایش برازش مناسب منحنی روی دادهها (مقدار بزرگتر بهتر است) |
برای ظاهر سازی منحنی روند، گامهای زیر را باید طی کنیم. البته فرض کردهایم که منحنی یا نمودار مربوط به زوج x,y را قبلا ترسیم کردهایم. نوع نمودار باید یکی از حالتهای «نمودار ستونی» (Column)، «میلهای» (Bar) یا «نمودار پراکندگی» (Scatter X,Y) باشد. در غیر اینصورت امکان نمایش خط یا «منحنی روند» (Trendline) روی نمودارهای دیگر وجود ندارد.
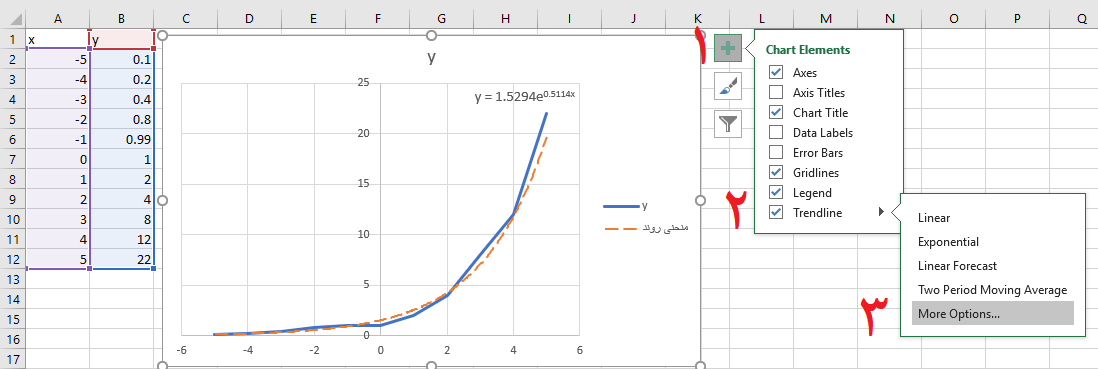
- با استفاده از علامت + که در کنار نمودار ظاهر شده، فهرست عناصر نمودار (Chart Elements) را باز کنید.
- گزینه Trendline را فعال کنید. به این ترتیب یک خط روند به صورت پیشفرض به نمودارتان اضافه خواهد شد.
- اگر نشانگر را روی علامت → در این قسمت قرار دهید، لیستی از توابع پیشنهادی اکسل برای رسم منحنی ظاهر میشود. برای دسترسی به قاب انتخاب نوع تابع (مطابق با تصویر ۱) گزینه More options را انتخاب کنید.
این مراحل در تصویر ۲ به خوبی مشخص شدهاند. به یاد داشته باشید که ابتدا باید یک نمودار در کاربرگ اکسل داشته و آن را انتخاب کرده باشید تا عملیات گفته شده، قابل اجرا باشند.
پس از اینکه قاب Trendline Format ظاهر شد، تنظیمات را به دلخواه (مطابق با جدول ۱ و ۲) انجام داده تا منحنی روند یا معادله منحنی براساس پارامترهای تعیین شده، نمایش داده شود. در ادامه با ذکر مثالهایی، به بررسی برازش دادهها و پیدا کردن پارامترهای معادله منحنی در اکسل برای هر یک از توابع فوق خواهیم پرداخت.
رسم معادله منحنی نمایی
برای رسم معادله منحنی در اکسل به صورت نمایی، باید دادههایی داشته باشیم که دارای رشد سریع و صعودی باشد. همانطور که در جدول ۱ مشاهده کردید، پارامترهای این تابع $$c$$ و $$b$$ هستند. به این نکته توجه داشته باشید که هنگام استفاده از این منحنی، مقادیر مولفه دوم یعنی $$y$$ باید همگی مثبت باشند و گرنه امکان استفاده از رسم معادله منحنی در اکسل به صورت نمایی میسر نخواهد شد.
به جدول اطلاعاتی که در کاربرگ اکسل ثبت شده و در تصویر ۲ قابل مشاهده است، توجه کنید. با توجه به ساختاری که زوجهای x و y دارند، روند یا معادله منحنی نمایی برایشان مناسب است. همانطور که میبینید با انتخاب تنظیماتی که در تصویر ۳ دیده میشود، معادله خط روند و همچنین نمایش «راهنمای نمودار» (Legend) به درک بهتر خطوط نمودار کمک شایانی کردهاند.
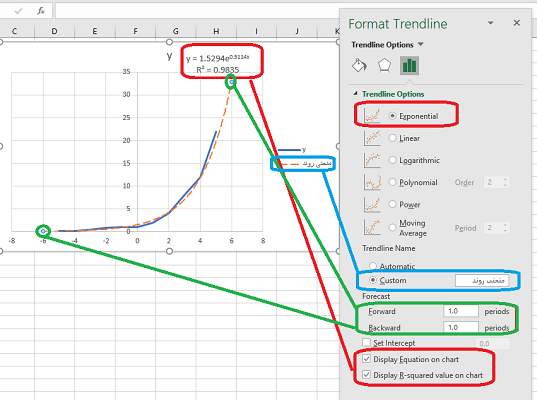
دادههای مربوط به ترسیم این منحنی، با مقادیری که در تصویر ۲ دیده میشود، مطابقت دارد. همانطور که میبینید، مقادیری نیز در این نمودار پیشبینی (برونیابی) شدهاند. دور این نقطهها در نمودار یک دایره سبز رنگ کشیدهایم. یک واحد قبل از کوچکترین مقدار (در قسمت backward) و یک واحد بعد از آخرین داده (در قسمت Forward) تعیین شده که مقدار برونیابی شده روی معادله منحنی در اکسل را مشخص کردهاند. توجه داشته باشید که رابطه یا تابع نمایی به کار رفته برای درون یابی یا برون یابی به صورت زیر است.
$$ \large y = 1.5294 e^{(0.5114\; x)} $$
پس پارامترها به صورت $$b=0.5114$$ و $$c= 1.5294$$ خواهند بود. از طرفی بزرگ بودن «ضریب تعیین» (R Square) که برابر با $$R^2 = 0.9835$$ است، نشانگر برازش مناسب تابع نمایی روی چنین دادههایی است. از آنجایی که عرض از مبدا تعیین نشده، محاسبه محل برخورد نمودار با محور عمودی، به طور خودکار محاسبه شده.
به یاد داشته باشید که در این نمودار و نمودارهای بعدی، منحنی خط روند با رنگ نارنجی (با خطو چین) و نمودار دادههای اصلی با رنگ آبی مشخص شده است.
رسم معادله منحنی خطی
این بار با همان دادههای مربوط به تصویر ۲، یک معادله خطی را برازش میدهیم. همانطور که در تصویر ۴ مشاهده میکنید، معادله منحنی خطی نتوانسته پوشش مناسبی با نمودار مربوط به دادهها داشته باشد. از طرفی مشخص است ضریب تعیین، مقداری کوچک بوده ($$R^2 = 0.6703$$) و نامناسب بودن تابع خطی را برای برازش منحنی و پیشبینی نشان میدهد.
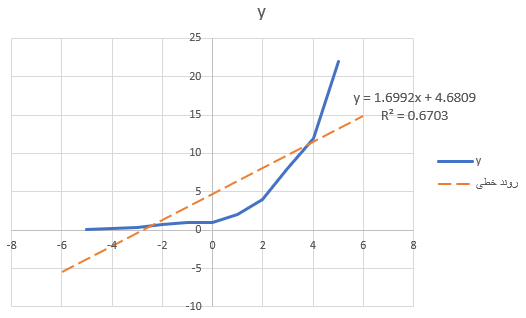
پارامترها و معادله منحنی در اکسل برای حالت خطی به صورت زیر است.
$$ \large y = 1.6992 \; x + 4.6809 $$
واضح است که $$m = 1.6992$$ و $$b = 4.6809$$ خواهد بود. عرض از مبدا یا محل برخورد این تابع با محور عمودی، همان مقدار $$b$$ خواهد بود.
رسم معادله منحنی چند جمله ای
در تصویر ۴، برای دادههای مربوط به قسمت قبل، یک چند جملهای مرتبه ۴ برازش کردهایم. همانطور که میبینید، ($$R^2 = 0.9967$$) نشانگر برازش مناسب این تابع روی دادهها است. همچنین مقادیر پیش بینی نیز برای یک گام عقب یا جلوتر از دادهها، مناسب به نظر میرسد.
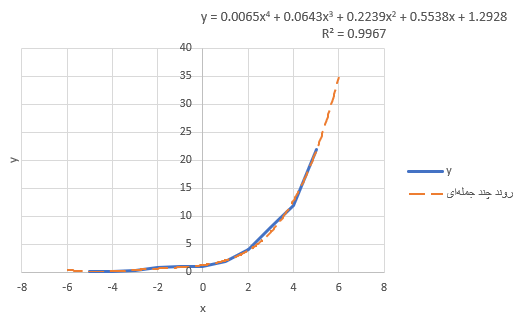
معادله و پارامترهای این مدل به صورت زیر خواهند بود. برخورد این تابع با محور عمودی نیز در نقطه $$(0 , 1.2928)$$ رخ داده است.
$$ \large y = 0.00065x^4 + 0.0643 x^3 + 0.2239 x^2 + 0.5538 x + 1.2928 $$
البته هر چه درجه چند جملهای را افزایش دهیم، برازش بهتری خواهیم داشت ولی در عوض پیچیدگی مدل را هم افزایش دادهایم و کار محاسباتی بیشتری برای برآورد پارامترها لازم است. بنابراین معمولا به دنبال حداقل درجهای از چند جملهای هستیم که بیشترین ضریب تعیین ($$R^2$$) را داشته باشد و با افزایش یک جمله دیگر به چند جملهای، ضریب تعیین تغییر محسوسی نکرده باشد.
رسم معادله منحنی میانگین متحرک
توجه داشته باشید که روش میانگین متحرک (Moving average) یک روش هموار سازی برای توابع است. به این ترتیب هر نقطه از نمودار هموار شده، برآیندی از نقاط اطراف خود خواهد شد و به این ترتیب نمودار ترسیم شده از نقطهها، بدون شکستی زیاد، ظاهر میشوند. در تصویر ۶ منحنی میانگین متحرک برای دادههای قسمت قبل ترسیم شده است.
البته توجه دارید که این نمودار براساس میانگین متحرک مرتبه دو شکل گرفته. به این معنی که هر نقطه از نمودار هموار شده، نتیجه میانگین دو قبلی از دادهها است. اگر مرتبه میانگین متحرک را افزایش دهیم، تعداد نقطههای نمودار هموار شده کاهش مییابد و ممکن است نتواند برازش مناسبی ارائه کند.
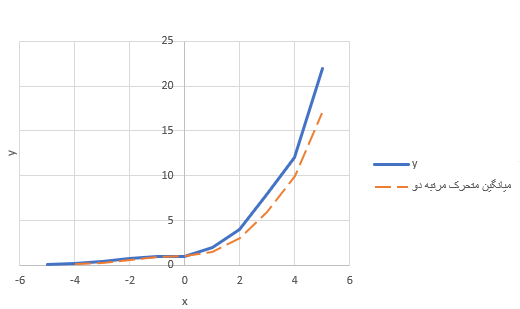
توجه دارید که در این حالت امکان نمایش معادله منحنی رسم شده و همچنین بدست آوردن ضریب تعیین و نمایش آن در کنار نمودار اکسل وجود ندارد. معادله و روش محاسبه روند میانگین متحرک را در جدول ۱، مشاهده کنید.
نکته: چون متغیر y، شامل مقادیر منفی است، منحنی یا تابع لگاریتمی و توانی را نمیتوان به عنوان تابع روند برای این مسئله به کار برد.
خلاصه و جمعبندی
در این متن با چند روش برازش یا پیدا کردن معادله منحنی در اکسل آشنا شدیم. معادله منحنی در اکسل به اصلاح «خط روند» (Trend line) نامیده میشود، هر چند ممکن است این روند کاملا خطی هم نباشد. بنابراین اصطلاح منحنی روند یا درون یابی (برون یابی) شاید عبارت بهتری برای این امر باشد. توابعی که پارامترهای آن را برای منحنی روند در اکسل مورد بررسی قرار دادیم، توابع پرکاربرد در ریاضی هستند. برای مثال توابع نمایی، لگاریتمی و چند جملهای، از موارد بودند که در اکثر مواقع برای درون یابی یا برونیابی به کار میروند.










