تعادل شیمیایی — از صفر تا صد

در یک واکنش شیمیایی، به حالتی تعادل شیمیایی می‌گویند که در آن، واکنش‌دهنده‌ها و فرآورده‌ها در غلظت‌هایی حضور دارند که با گذشت زمان، تغییر نمی‌کنند. در نتیجه، شاهد تغییرات در خواص سیستم نخواهیم بود. به طور معمول،‌ این حالت زمانی بوجود می‌آید که واکنش رفت و واکنش برگشت، هر دو با یک سرعت انجام شوند. در حقیقت، سرعت واکنش‌های رفت و برگشت صفر نیست بلکه یکسان است. بنابراین، هیچ تغییری در غلظت واکنش‌دهنده‌ها و فرآورده‌ها نخواهیم داشت. به این حالت،‌ «تعادل دینامیک» (Dynamic Equilibriuim) یا تعادل پویا می‌گویند.

مبانی تعادل شیمیایی

همانطور که در بالا به آن اشاره شد، تعادل شیمیایی حالتی است که در آن، سرعت واکنش رفت با سرعت واکنش برگشت برابر است.

فیلم آموزش شیمی فیزیک – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

واکنش اساسی زیر را در نظر بگیرید:

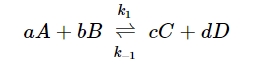
سرعت واکنش رفت را می‌توان به کمک رابطه زیر نشان داد:

$$= -k_1[A]^a[B]^b = k_{-1}[C]^c[D]^d$$ سرعت

که در رابطه بالا، $$k_1$$ و $$k_{-1}$$، «ثابت‌های واکنش» (Reaction Constants) به ترتیب برای واکنش‌های رفت و برگشت هستند. توجه داشته باشید که مقدار k، در واکنش‌ها و دماهای مختلف، متفاوت خواهد بود.

زمانی که سرعت صفر باشد، غلظت‌های خالص A، B، C و D با یکدیگر در تعادل قرار دارند. در نتیجه، اگر تغییری در سیستم،‌ بواسطه تغییر در غلظت، دما یا فشار اتفاق بیافتد، تعادل در جهت توازن این تغییرات پیش خواهد رفت و تعادل جدیدی بر مبنای اصل لوشاتلیه بوجود خواهد آمد. به این نکته توجه داشته باشید که حضور کاتالیزور، هیچ جابجایی را در تعادل صورت نمی‌دهد و تنها سبب می‌شود تا واکنش، زودتر به تعادل برسد چراکه کاتالیزورها تنها انرژی فعال‌سازی را کاهش می‌دهند.

تعریف ساده تعادل شیمیایی

در یک واکنش شیمیایی، زمانی که غلظت واکنش‌دهنده‌ها و فرآورده‌ها با پیشرفت واکنش، ثابت شوند، می‌گوییم که این واکنش به نقطه تعادل رسیده است. در این خصوص باید گفت که ثبات برخی از خواص قابل اندازه‌گیری همچون غلظت، رنگ، فشار و چگالی، بیانگر حالت تعادل هستند. این حالت تعادل را نوعی تعادل پویا می‌دانند چراکه واکنش به طور پیوسته در حال انجام است و ثبات مقادیر به معنای توقف واکنش نیست بلکه در حقیقت، سرعت واکنش‌های رفت و برگشت یکسان شده‌اند.

مثالی از این تعریف را می‌توان در تصویر زیر مشاهده کرد. در این تصویر، واکنش تعادلی دی‌اکسید نیتروژن با $$N _ 2 O _ 4$$ نشان داده شده است. نمودارهای سرعت-زمان و غلظت-زمان، به خوبی محل رسیدن به تعادل را نشان داده‌اند.

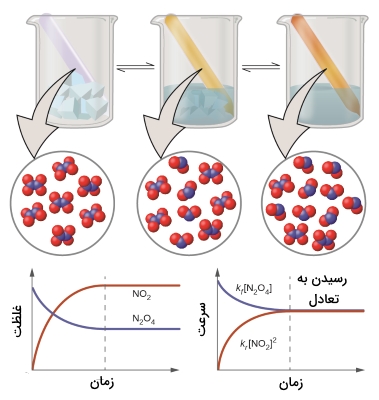
تعادل شیمیایی و جهت پیشرفت واکنش

تعادل دینامیک به ما کمک می‌کند تا تشخیص دهیم که یک واکنش، در کدامیک از جهت‌های رفت یا برگشت خود‌به‌خودی است. برای توضیح این امر، سه کمیت را باید تعریف کنیم: ثابت تعادل $$(K)$$، خارج قسمت واکنش $$(Q)$$ و انرژی آزاد گیبس $$(dG_r)$$. روابط بین $$K$$ و $$Q$$ در زیر آورده شده‌اند:

$$K = \frac{a_C^ca_D^d}{a_A^aa_B^b}$$

$$Q = \frac{a_C^ca_D^d}{a_A^aa_B^b}$$

مقادیر $$K$$ و $$Q$$  به ترتیب در نقطه تعادل و در هر نقطه از واکنش تعریف می‌شوند. در روابط بالا، $$a_c$$ و $$a_D$$ به ترتیب مرتبط با «فعالیت» (Activity) $$C$$ و $$D$$ هستند. انرژی آزاد گیبس واکنش، مقادیر $$Q$$  و $$T$$ را طبق واکنش زیر به یکدیگر مرتبط می‌کند که در این رابطه $$dG_r^{\circ}$$، انرژی آزاد گیبس برای واکنش در شرایط استاندارد است:

$$dG_r = dG_r^{\circ} + RT\ln{Q}$$

زمانی که $$dG_r$$ منفی باشد، واکنشِ رفت در جهت خود‌به‌خودی خواهد بود و زمانی که این عبارت مثبت باشد، واکنش برگشت خود‌به‌خودی است. این شرایط به دلیل انحراف $$Q$$ از $$K$$ و اصل لوشاتلیه در دمای استاندارد بوجود می‌آید. زمانی که $$Q$$ بزرگتر از $$K$$ باشد، فرآورده بیشتری نسبت به نقطه تعادل خواهیم داشت و بنابر اصل لوشاتلیه، تعادل به سمت واکنش‌دهنده‌ها جابجا خواهد شد.

به عبارت دیگر، واکنش برگشت به صورت خود‌به‌خودی و متناظر با $$dG_r$$ خواهد بود. زمانی که $$Q$$ کوچک‌تر از $$K$$ باشد،‌ واکنش‌دهنده بیشتری نسبت به نقطه تعادل خواهیم داشت و واکنش به طرف تولید فرآورده پیش‌ خواهد رفت و بنابراین، واکنش، در جهت رفت، خود‌به‌خودی و متناظر با $$dG_r$$ منفی است. به کمک نمودار زیر می‌توان رابطه بین $$Q$$ و $$dG_r$$ را نشان داد:

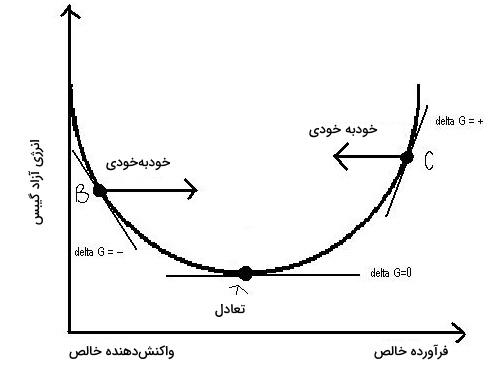
تعادل شیمیایی و ترمودینامیک

در فشار و دمای ثابت، انرژی آزاد گیبس برای یک واکنش، تنها به «مقدار واکنش» (Extent of Reaction) وابسته است و بر اساس قانون دوم ترمودینامیک می‌توان آن را کاهش داد.

فیلم آموزش ترمودینامیک 1 – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

این بدان معنی است که در صورت وقوع واکنش، مشتق انرژی آزاد گیبس نسبت به مقدار واکنش، باید منفی باشد. مقدار این مشتق در نقطه تعادل شیمیایی برابر با صفر است.

$$\left({\frac {dG}{d\xi }}\right)_{T,p}=0~$$

می‌توان نشان داد که در این شرایط،‌ مجموع پتانسیل‌های شیمیایی فرآورده‌ها با مجموع پتانسیل شیمیایی واکنش‌دهنده‌ها یکسان است. در نتیجه، مجموع انرژی‌های گیبس واکنش‌دهنده‌ها با فرآورده‌ها باید مقداری برابر داشته باشند. با تعریف معادله واکنش و ضرایب استوکیومتری، می‌توان رابطه تساوی انرژی‌های گیبس در واکنش‌دهنده‌ها و فرآورده‌ها را نوشت:

$$α A + β B ⇌ σ S + τ T$$

$$\alpha \mu_{\mathrm{A}}+\beta \mu_{\mathrm{B}}=\sigma \mu_{\mathrm{S}}+\tau \mu_{\mathrm{T}}$$

در رابطه بالا، $$\mu$$، پتانسیل شیمیایی نام دارد. پتانسیل شیمیایی واکنش‌دهنده A تابعی از «فعالیت» (Activity) یا اکتیویته آن واکنش‌دهنده ذکر می‌شود که به صورت {A} در رابطه زیر آورده شده و در این رابطه، $$\mu_{A}^{\ominus}$$، پتانسیل شیمیایی استاندارد است.

$$\mu_{\mathrm{A}}=\mu_{A}^{\ominus}+R T \ln \{\mathrm{A}\}$$

با استفاده از روابط انرژی آزاد گیبس و رابطه اساسی ترمودینامیک، به تعریف زیر خواهیم رسید:

$$dG=Vdp-SdT+\sum _{i=1}^{k}\mu _{i}dN_{i}$$

اگر در فرمول بالا، رابطه $$dNi = νi dξ$$ را قرار دهیم، در فشار و دمای ثابت، رابطه بالا را به صورت زیر می‌توان نوشت:

$${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}=\sum _{i=1}^{k}\mu _{i}\nu _{i}=\Delta _{\mathrm {r} }G_{T,p}}$$

این رابطه بیانگر تغییرات انرژی آزاد گیبس در واکنش است. بر این اساس خواهیم داشت:

$${\displaystyle \Delta _{\mathrm {r} }G_{T,p}=\sigma \mu _{\mathrm {S} }+\tau \mu _{\mathrm {T} }-\alpha \mu _{\mathrm {A} }-\beta \mu _{\mathrm {B} }\,}$$

با جایگذاری پتانسیل شیمیایی در رابطه فوق، به رابطه زیر می‌رسیم:

$$\Delta_{\mathrm{r}} G_{T, p}=\left(\sigma \mu_{\mathrm{S}}^{\mathrm{O}}+\tau \mu_{\mathrm{T}}^{\mathrm{O}}\right)-\left(\alpha \mu_{\mathrm{A}}^{\mathrm{Q}}+\beta \mu_{\mathrm{B}}^{\mathrm{O}}\right)\\+(\sigma R T \ln \{\mathrm{S}\}+\tau R T \ln \{\mathrm{T}\})-(\alpha R T \ln \{\mathrm{A}\}+\beta R T \ln \{\mathrm{B}\})$$

در نهایت، رابطه فوق به شکل زیر تبدیل خواهد شد:

$${\displaystyle \Delta _{\mathrm {r} }G_{T,p}=\sum _{i=1}^{k}\mu _{i}^{\ominus }\nu _{i}+RT\ln {\frac {\{\mathrm {S} \}^{\sigma }\{\mathrm {T} \}^{\tau }}{\{\mathrm {A} \}^{\alpha }\{\mathrm {B} \}^{\beta }}}}$$

$${\displaystyle \sum _{i=1}^{k}\mu _{i}^{\ominus }\nu _{i}=\Delta _{\mathrm {r} }G^{\ominus }}$$

رابطه بالا بیانگر تغییرات انرژی آزاد گیبس استاندارد برای واکنش است که آن را به کمک جداول ترمودینامیکی می‌توان محاسبه کرد. خارج قسمت واکنش نیز از رابطه زیر بدست می‌آید:

$${\displaystyle Q_{\mathrm {r} }={\frac {\{\mathrm {S} \}^{\sigma }\{\mathrm {T} \}^{\tau }}{\{\mathrm {A} \}^{\alpha }\{\mathrm {B} \}^{\beta }}}}$$

بنابراین، خواهیم داشت:

$${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}=\Delta _{\mathrm {r} }G_{T,p}=\Delta _{\mathrm {r} }G^{\ominus }+RT\ln Q_{\mathrm {r} }}$$

با توجه به این‌که در حالت تعادل، داریم: $${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}=\Delta _{\mathrm {r} }G_{T,p}=0}$$، رابطه به شکل زیر تغییر پیدا می‌کند:

$${\displaystyle 0=\Delta _{\mathrm {r} }G^{\ominus }+RT\ln K_{\mathrm {eq} }}$$

$${\displaystyle \Delta _{\mathrm {r} }G^{\ominus }=-RT\ln K_{\mathrm {eq} }}$$

با بدست آوردن مقدار تغییرات انرژی آزاد گیبس، می‌توان ثابت تعادل را محاسبه کرد.

بحث در خصوص فعالیت (اکتیویته)

رابطه ثابت تعادل را می‌توان به صورت حاصلضرب «خارج قسمت غلظت» (Concentration Quotient)، $$K_C$$ و ضریب فعالیت $$Γ$$ نوشت:

$${\displaystyle K={\frac {[\mathrm {S} ]^{\sigma }[\mathrm {T} ]^{\tau }...}{[\mathrm {A} ]^{\alpha }[\mathrm {B} ]^{\beta }...}}\times {\frac {{\gamma _{\mathrm {S} }}^{\sigma }{\gamma _{\mathrm {T} }}^{\tau }...}{{\gamma _{\mathrm {A} }}^{\alpha }{\gamma _{\mathrm {B} }}^{\beta }...}}=K_{\mathrm {c} }\Gamma }$$

در رابطه بالا، $$[A]$$، غلظت واکنش‌دهنده A است. روش‌های مختلفی برای محاسبه ضریب فعالیت $$( γ)$$ یا اکتیویته وجود دارند. به طور معمول، مقدار عبارت $$Γ$$ را ثابت فرض می‌کنند و از رابطه خارج قسمت غلظت به جای ثابت تعادل ترمودینامیکی بهره می‌گیرند. همچنین، به طور معمول از عبارت ثابت تعادل به جای رابطه دقیق‌تر خارج قسمت غلظت استفاده می‌شود.

برای واکنش در فاز گاز، فشار جزئی را به جای غلظت و ضریب فوگاسیته را به جای ضریب فعالیت بکار می‌گیریم. در کاربردهای صنعتی، به طور مثال، به هنگام تهیه آمونیاک، فوگاسیته را باید مد نظر قرار داد که این عبارت، حاصلضرب فشار جزئی در ضریب فوگاسیته است. پتانسیل شیمیایی اجزا در فاز گازی، از رابطه زیر بدست می‌آید:

$${\displaystyle \mu =\mu ^{\ominus }+RT\ln \left({\frac {f}{\mathrm {bar} }}\right)=\mu ^{\ominus }+RT\ln \left({\frac {p}{\mathrm {bar} }}\right)+RT\ln \gamma }$$

بنابراین، رابطه کلی که ثابت تعادل را تعریف می‌کند، برای محلول‌ها و گازها قابل استفاده خواهد بود.

خارج قسمت غلظت

در یک محلول آبی، ثابت تعادل را به طور معمول در حضور یک الکترولیت خنثی همچون سدیم نیترابت یا پتاسیم پرکلرات تعیین می‌کنند.

فیلم آموزش ترمودینامیک 2 – مرور و تست کنکور ارشد در فرادرس

کلیک کنید

قدرت یونی یک محلول، از رابطه زیر بدست می‌آید. در این رابطه، $$c_i$$ و $$z_i$$، به ترتیب، غلظت و بار یونی یون $$i$$ هستند که این مجموع برای N نوع از ذره باردار محاسبه می‌شود:

$${\displaystyle I={\frac {1}{2}}\sum _{i=1}^{N}c_{i}z_{i}^{2}}$$

زمانی که غلظت نمک محلول، بسیار بیشتر از «غلظت‌های تحیلی» (Analytical Concentration) واکنش‌دهنده‌ها باشد، یون‌های حاصل از انحلال نمک، قدرت یونی را تعیین می‌کنند و این قدرت یونی، به طور موثری ثابت است. از آن جایی که ضریب فعالیت، به قدرت یونی بستگی دارد، درنتیجه، ضریب فعالیت اجزای یک محلول،‌ مستقل از غلظت خواهد بود. بنابراین، با این توضیح، فرض ثابت بودن $$Γ$$ توجیه می‌شود. لازم به ذکر است که خارج قسمت غلظت، مضرب ساده‌ای از ثابت تعادل خواهد بود که می‌توان آن را به صورت زیر تعریف کرد:

$${\displaystyle K_{\mathrm {c} }={\frac {K}{\Gamma }}}$$

مقدار $$K_c$$ با قدرت یونی تغییر می‌کند. اگر در مقادیر مختلف قدرت یونی، این عبارت اندازه‌گیری شود، مقدار مختلف آن‌را برای رسیدن به قدرت یونی صفر می‌توان برون‌یابی کرد. خارج قسمت غلظتی که از این روش بدست بیاید را نیز به عنوان ثابت تعادل ترمودینامیکی می‌شناسند که البته برای استفاده از مقادیر آن در شرایط مختلف، نیاز به تصحیحاتی وجود دارد.

مخلوط‌های فراپایدار

یک مخلوط ممکن است حتی در حالتی به غیر از حالت تعادلی، تمایلی برای تغییر نداشته باشد که در اینصورت به آن، مخلوط «فراپایدار» (Metastable) می‌گویند. به طور مثال، مخلوط $$SO_2$$ و $$O_2$$ نوعی مخلوط فراپایدار است چراکه نوعی «مانع سینتیکی» (Kinetic Barrier) برای تشکیل فرآورده $$SO_3$$ وجود دارد و نوعی «انرژی فعال‌سازی» (Activation Energy) محسوب می‌شود که با استفاده از کاتالیزور می‌توان بر آن غلبه کرد.

$$2 SO2 + O2 ⇌ 2 SO3$$

به طور مشابه، تشکیل بی‌کربنات از دی‌اکسید کربن و آب، در شرایط معمول، با سرعت بسیار کمی پیش می‌رود، اما با استفاده از کاتالیزور آنزیمی، می‌توان سرعت آن‌را افزایش داد.

$$\mathrm{CO}_{2}+2 \mathrm{H}_{2} \mathrm{O} \rightleftharpoons \mathrm{HCO}_{3}^{-}+\mathrm{H}_{3} \mathrm{O}^{+}$$

مواد خالص

زمانی که مواد خالص جامد و مایع را در تعادل شیمیایی دخیل کنیم، با توجه به این‌که مقدار عددی اکتیویته را ۱ در نظر می‌گیریم، میزان فعالیت این مواد در ثابت تعادل دیده نمی‌شوند. با بکارگیری فرمول کلی ثابت تعادل در محلول رقیق استیک اسید در آب، خواهیم داشت:

$$\mathrm{CH}_{3} \mathrm{CO}_{2} \mathrm{H}+\mathrm{H}_{2} \mathrm{O} \rightleftharpoons \mathrm{CH}_{3} \mathrm{CO}_{2}^{-}+\mathrm{H}_{3} \mathrm{O}^{+}$$

$${\displaystyle K_{\mathrm {c} }={\frac {\mathrm {[{CH_{3}CO_{2}}^{-}][{H_{3}O}^{+}]} }{\mathrm {[{CH_{3}CO_{2}H}][{H_{2}O}]} }}}$$

برای محلول‌های بسیار غلیظ، آب را می‌توان به عنوان یک مایع خالص و فعالیت آن را برابر با عدد ۱ در نظر گرفت. در نتیجه، رابطه ثابت تعادل را به صورت زیر خواهیم نوشت:

$${\displaystyle K={\frac {\mathrm {[{CH_{3}CO_{2}}^{-}][{H_{3}O}^{+}]} }{\mathrm {[{CH_{3}CO_{2}H}]} }}=K_{\mathrm {c} }}$$

به طور مثال، می‌توان به واکنش «خودیونش آب» (Self-Ionization of Water) اشاره کرد:

$$2 \mathrm{H}_{2} \mathrm{O} \rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}+\mathrm{OH}^{-}$$

با توجه به اینکه آب، نوعی حلال و فعالیت آن برابر با ۱ است، ثابت خودیونش آب به صورت زیر تعریف می‌شود:

$${\displaystyle K_{\mathrm {w} }=\mathrm {[H^{+}][OH^{-}]} }$$

میزان $$K_w$$ با تغییر قدرت یونی یا دما، تغییر پیدا می‌کند. غلظت‌های $$H^+$$ و $$OH^-$$، مقادیر مستقلی نیستند. همچنین، در توصیف ثابت تعادل، به جای $$[OH^-]$$ از عبارت $$K_W [H ^ +]^ {-1}$$ استفاده می‌شود.

جامدات نیز اگر به صورت خالص در نظر گرفته شوند و فعالیتی برابر با ۱ داشته باشند، در معادله ثابت تعادل حضور نخواهند داشت. به عنوان نمونه می‌توان به «واکنش بودوراد» (Boudouard Reaction) اشاره کرد.

$$2 CO ⇌ CO_2 + C$$

که بدون در نظر گرفتن کربن جامد، رابطه ثابت تعادل، به صورت زیر نوشته خواهد شد:

$${\displaystyle K_{\mathrm {c} }={\frac {\mathrm {[CO_{2}]} }{\mathrm {[CO]^{2}} }}}$$

تعادل شیمیایی چندگانه

اسید دو پروتونه $$H_2A$$ را در نظر بگیرید. زمانی که در آب حل شود، مخلوط حاصل شامل $$H_2A$$،‌ $$HA^-$$ و $$A^{2-}$$ خواهد بود. این واکنش، شامل تعادلی دو مرحله‌ای به صورت زیر است:

$$\begin{array}{ll} {\mathrm{H}_{2} \mathrm{A} \rightleftharpoons \mathrm{HA}^{-}+\mathrm{H}^{+}:} & {K_{1}=\frac{\left[\mathrm{HA}-\mathrm{l} \mathrm{H}^{+}\right]}{\left[\mathrm{H}_{2} \mathrm{A}\right]}} \\ {\mathrm{HA}^{-} \rightleftharpoons \mathrm{A}^{2-}+\mathrm{H}^{+}:} & {K_{2}=\frac{\left[\mathrm{A}^{2}-\right]\left[\mathrm{H}^{+}\right]}{[\mathrm{HA}-]}} \end{array}$$

$$K_1$$ و $$K_2$$ را به عنوان ثابت تعادل مرحله‌ای می‌شناسند. ثابت تعادل کلی $$(β_D)$$، حاصلضرب ثابت‌های تعادل مرحله‌ای است.

$$\mathrm{H}_{2} \mathrm{A} \rightleftharpoons \mathrm{A}^{2-}+2 \mathrm{H}^{+}\\ \quad \beta_{\mathrm{D}}=\frac{\left[\mathrm{A}^{2-}\right]\left[\mathrm{H}^{+}\right]^{2}}{\left[\mathrm{H}_{2} \mathrm{A}\right]}=K_{1} K_{2}$$

تاثیر دما در تعادل شیمیایی

تاثیر دما بر ثابت تعادل را به کمک «معادله وانت‌هوف» (Van't Hoff Equation) بیان می‌کنند.

$$\frac{d \ln K}{d T}=\frac{\Delta H_{\mathrm{m}}^{\circ}}{R T^{2}}$$

فیلم آموزش شیمی فیزیک – حل مساله در فرادرس

کلیک کنید

در نتیجه، برای زمانی که واکنش، گرماده و آنتالپی منفی باشد، $$K$$ با افزایش دما، کاهش می‌یابد اما برای واکنش‌های گرماگیر، با افزایش دما،‌ $$K$$ کاهش خواهد یافت.

انواع تعادل شیمیایی

تعادل شیمیایی را به طور خلاصه می‌توان در دو دسته تعادل همگن و تعادل ناهمگن دسته‌بندی کرد. تعادل شیمیایی همگن به واکنش‌های تعادلی می‌گویند که در آن‌ها، واکنش‌دهنده و فرآورده هر دو در یک فاز قرار داشته باشند.

ترکیب یک مخلوط تعادلی

برای محاسبه ترکیب یک مخلوط، راه‌های بسیاری وجود دارد. یکی از راه‌های معمول، استفاده از جداول ICE است که در محلول‌های بافر، روش استفاده از آن را توضیح داده‌ایم. به طور کلی، سه روش برای محاسبه ترکیب یک مخلوط تعادلی وجود دارد.

• استفاده از پتانسیل شیمیایی
• کمینه کردن انرژی گیبس سیستم
• استفاده از موازنه جرم

معادلات موازنه جرم

به طور کلی، این نوع از محاسبات، پیچیده است. به طور مثال، در خصوص یک اسید دو پروتونه، به هنگام انحلال $$H_2A$$ در آب، دو واکنش‌دهنده را تحت عنوان باز مزدوج $$A^-$$ و پروتون $$H ^ +$$ می‌توان مشخص کرد. واکنش‌های موازنه جرم زیر را می‌توان در این خصوص بکار برد:

$$\begin{array}{l} {T_{\mathrm{A}}=[\mathrm{A}]+[\mathrm{HA}]+\left[\mathrm{H}_{2} \mathrm{A}\right]} \\ {T_{\mathrm{H}}=[\mathrm{H}]+[\mathrm{HA}]+2\left[\mathrm{H}_{2} \mathrm{A}\right]-[\mathrm{OH}]} \end{array}$$

در رابطه بالا، $$T_A$$ غلظت کلی جزء A به شمار می‌آید. توجه داشته باشید که به هنگام نوشتن این نوع از معادلات، می‌توان از نوشتن علامت بارها خودداری کرد. زمانی که ثابت‌های تعادل را بدانیم و غلظت‌های کلی نیز تعیین شده باشند، دو معادله و دو مجهول خواهیم داشت که غلظت‌های $$[A]$$ و $$[H]$$ هستند. رابطه بالا را به صورت زیر می‌توان نوشت:

$$\begin{aligned} &T_{\mathrm{A}}=[\mathrm{A}]+\beta_{1}[\mathrm{A}][\mathrm{H}]+\beta_{2}[\mathrm{A}][\mathrm{H}]^{2}\\ &T_{\mathrm{H}}=[\mathrm{H}]+\beta_{1}[\mathrm{A}][\mathrm{H}]+2 \beta_{2}[\mathrm{A}][\mathrm{H}]^{2}-K_{w}[\mathrm{H}]^{-1} \end{aligned}$$

بنابراین، غلظت کمپلکس‌ها را می‌توان از طریق غلظت‌های آزاد و ثابت‌های تعادل محاسبه کرد. معادله کلی برای تمام سیستم‌ها با دو واکنش‌دهنده به صورت زیر خواهد بود:

$$\begin{aligned} &T_{\mathrm{A}}=[\mathrm{A}]+\sum_{i} p_{i} \beta_{i}[\mathrm{A}]^{p_{i}}[\mathrm{B}]^{q}\\ &T_{\mathrm{B}}=[\mathrm{B}]+\sum q_{i} \beta_{i}[\mathrm{A}]^{p_{i}}[\mathrm{B}]^{q_{i}} \end{aligned}$$

اسیدهای چند‌پروتونه

محاسبه ترکیب محلولی شامل واکنش‌دهنده $$A$$ و $$H$$ را می‌توان به سادگی و به صورت تابعی از pH محاسبه کرد. زمانی که [H] معلوم باشد، غلظت آزاد [A] را به کمک معادله موازنه جرم در A می‌توان نشان داد. تصویر زیر، نمونه‌ای از هیدرولیز آلومینیوم را نشان می‌دهد که در آن،‌ غلظت اجزا را به صورت نسبتی از آلومینیوم نشان داده است.

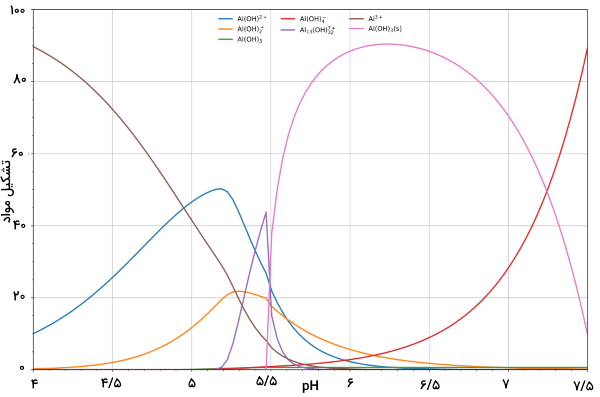
رسوب در محلول‌ها

تصویر بالا، تشکیل رسوبی را نشان می‌دهد که بخشی از اجزای اصلی در تعادل محلول نیست. در pH کمتر از ۵/۵، اجزای اصلی عبارتند از $$Al(OH)^{2+}$$، $$AlOH_2^+$$ و $$\mathrm{Al}_{13}(\mathrm{OH})_{32}^{7+}$$. با افزایش pH، $$AL(OH)_3$$ در محلول رسوب می‌کند. این اتفاق به دلیل انرژی شبکه زیاد در $$AL(OH)_3$$ بوقوع می‌پیوندد. این مورد را می‌توان به عنوان نمونه‌ای از اصلی لوشاتلیه بیان کرد. در حقیقت، افزایش غلظت یون هیدروکسید، سبب رسوب بیشتر آلومینیوم هیدروکسید می‌شود تا در اثر آن، با افزایش غلظت یون هیدروکسید مقابله شود. زمانی که غلظت هیدروکسید به اندازه کافی افزایش پیدا کنید، آلومینات $$(AL(OH)_3)$$ تشکیل می‌شود.

فیلم آموزش محلول سازی در آزمایشگاه در فرادرس

کلیک کنید

مثال معمول دیگری که در خصوص تشکیل رسوب می‌توان ذکر کرد، برهم‌کنش یک کاتیون فلزی با لیگاند آنیونی است که موجب تشکیل کمپلکسی خنثی به لحاظ الکتریکی می‌شود. اگر کمپلکس، آب‌گریز باشد، رسوب تشکیل خواهد شد. این اتفاق بین «دی‌متیل‌گلیوکسیم» (Dimethylglyoxime) و $$Ni^{2+}$$ رخ می‌دهد. در این حالت، انرژی شبکه جامد، مقدار زیادی ندارد اما بیشتر از انرژی «حلال‌پوشی» (Solvation) مولکول دی‌متیل گلیوکسیم است.

کمینه کردن انرژی گیبس

در نقطه تعادل، تحت فشار و دمای ثابت و زمانی که هیچ نیروی خارجی نداشته باشیم، انرژی آزاد گیبس، کمترین مقدار خود را دارد:

$$dG=\sum _{j=1}^{m}\mu _{j}\,dN_{j}=0$$

پتانسیل شیمیایی در رابطه بالا را می‌توان بر اساس فعالیت$$(A_j)$$ نیز بیان کرد که در این رابطه، $${\displaystyle \mu _{j}^{\ominus }}$$، پتانسیل شیمیایی در حالت استاندارد، R ثابت گازها و T، دمای مطلق است. :

$${\displaystyle \mu _{j}=\mu _{j}^{\ominus }+RT\ln {A_{j}}}$$

در یک سیستم بسته، هیچ ذره‌ای داخل یا خارج نمی‌شود. با وجود اینکه در چنین حالتی، ذرات ممکن است به طرق مختلفی با یکدیگر ترکیب شوند اما تعداد اتم هر عنصر، ثابت می‌ماند. این بدان معنی است که رابطه‌ای که در بالا برای کمینه کردن انرژی گیبس در نظر گرفتیم، متاثر از رابطه زیر خواهد بود:

$$\sum _{j=1}^{m}a_{ij}N_{j}=b_{i}^{0}$$

در این رابطه، a برابر تعداد اتم عنصر i در مولکول j است و $$b_ i ^ 0$$، تعداد کل اتم‌های عنصر i است. از آن‌جایی که یک سیستم بسته داریم، مقدار این عبارت، عددی ثابت خواهد بود. اگر تعداد k نوع اتم در سیستم داشته باشیم، به همان صورت هم تعداد k معادله خواهیم داشت. اگر یون‌ها را نیز دخیل کنیم، یک ردیف اضافی به ماتریس $$a_{ih}$$ اضافه خواهد شد که بیانگر بار هر مولکول و مجموع آن برابر با صفر است.

این مسئله یکی از مسائل استاندارد در بهینه‌سازی است که به عنوان «بهینه‌سازی محدود شده» (Constrained Optimization) شناخته می‌شود. معمول‌ترین روش برای حل آن، استفاده از ضرایب لاگرانژ است. رابطه‌ای به شکل زیر تعریف می‌کنیم. در این رابطه، $$\lambda _ i$$ ضرایب لاگرانژ برای هر عنصر هستند. این کار باعث می‌شود تا هرکدام از عبارات $$N_j$$ و $$\lambda _ i$$ به طور جداگانه بررسی شوند:

$${\mathcal {G}}=G+\sum _{i=1}^{k}\lambda _{i}\left(\sum _{j=1}^{m}a_{ij}N_{j}-b_{i}^{0}\right)=0$$

با استفاده از «حساب چند‌متغیره» (Multivariate Calculus) می‌توان نشان داد که تعادل شیمیایی تحت شرایط زیر برقرار خواهد بود:

$${\displaystyle 0={\frac {\partial {\mathcal {G}}}{\partial N_{j}}}=\mu _{j}+\sum _{i=1}^{k}\lambda _{i}a_{ij}}$$

$${\displaystyle 0={\frac {\partial {\mathcal {G}}}{\partial \lambda _{i}}}=\sum _{j=1}^{m}a_{ij}N_{j}-b_{i}^{0}}$$

در معادلات فوق، یک دستگاه m+k معادله با m+k مجهول داریم و در نتیجه، تا زمانی که در فشار و دمای مشخص، فعالیت‌های شیمیایی را به عنوان تابعی از غلظت داشته باشم، چنین معادلاتی را برای غلظت‌های تعادلی $$N_j$$ می‌توان حل کرد. این روش محاسبه غلظت‌های تعادلی، برای سیستم‌هایی با تعداد مولکول‌های مختلف کاربرد دارد.

کاربرد تعادل شیمیایی

هموگلوبین، نوعی پروتئین در خون انسان است که وظیفه حمل اکسیژن به سلول‌های دیگر را بر عهده دارد. واکنش زیر نشان می‌دهد که چگونه، هموگلوبین (Hb) با چهار اتم اکسیژن پیوند تشکیل می‌دهد که در ادامه، بدن انسان از این اکسیژن استفاده می‌کند.

$$\mathrm{Hb}(\mathrm{aq})+4 \mathrm{O}_{2}(\mathrm{g}) \leftrightharpoons \mathrm{Hb}\left(\mathrm{O}_{2}\right)_{4}$$

تا زمانی که اکسیژن تامین شود، تعادل نیز برقرار خواهد بود. در ارتفاعات زیاد همچون کوه‌ها که فشار هوا کاهش پیدا می‌کند، اکسیژن کمتری داریم. بنابر اصل لوشاتلیه، تعادل به طرف چپ پیش‌روی خواهد کرد. بنابراین، کسی که دچار کاهش اکسیژن در سلول‌های بدن شود،‌ دچار سرگیجه و بیهوشی می‌شود.

فیلم مجموعه آموزش دروس شیمی – از دروس دانشگاهی تا کاربردی در فرادرس

کلیک کنید

اگر این مطلب برای شما مفید بوده‌ است،‌ آموزش‌ها و مطالب زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس شیمی
• مجموعه آموزش‌های مهندسی شیمی
• آموزش شیمی عمومی
• قانون هس — به زبان ساده
• واکنش اکسایش کاهش (ردوکس) — به زبان ساده

^^