رسم نمودار دو بعدی در متلب (+ دانلود فیلم آموزش رایگان)

رسم نمودار دو بعدی و نمودار سهبعدی در متلب برای اکثر شاخههای علوم مهندسی و علوم محض از اهمیت ویژهای برخوردار است. با استفاده از نمودارهای دو بعدی، میتوان تاثیرات متغیرهای مستقل را روی توابع به شکل گرافیکی بررسی و تحلیل کرد. در این مقاله میخواهیم به بررسی ترسیم انواع نمودارهای دو بعدی در نرمافزار متلب بپردازیم. در ابتدا انواع روشهای رسم نمودارهای دو بعدی را بیان میکنیم و سپس نحوه زیباسازی و تنظیمات نمودارها را شرح میدهیم.
رسم نمودار دو بعدی در متلب با دستور ezplot
نحوه استفاده از این دستور برای رسم نمودار دو بعدی در متلب به شکل زیر است:
ورودی اول در این دستور، فرمول تابع مورد نظر است که به صورت یک رشته وارد میشود. برای مثال، اگر تابع به فرم باشد، آنگاه مقدار String به شکل وارد میشود. ورودی دوم، بازه نمایش نمودار تابع است که مقدار حداقل و حداکثر آن را وارد میکنیم. برای مثال برنامه زیر نمودار این تابع را در دو دوره تناوب آن رسم میکند.
1clc;
2clear;
3close all;
4%%
5figure(1);
6ezplot('sin(x)+sin(3*x)/3+sin(5*x)/5' , [0 4*pi]) ; %#okنمودار به شکل زیر رسم میشود:
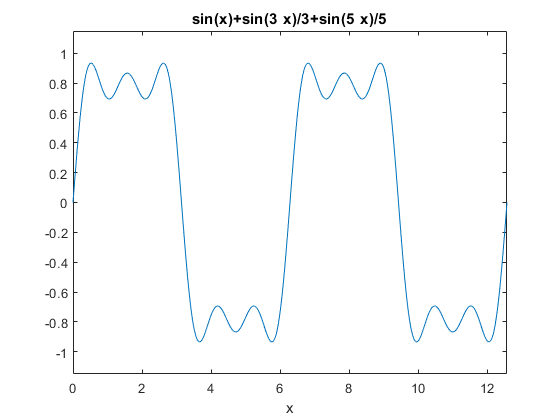 " width="560" height="420">
" width="560" height="420">از این دستور میتوان برای رسم توابع پارامتری نیز استفاده کرد. در این شرایط نحوه استفاده از دستور ezplot به شکل زیر است:
ورودیهای و ، مانند حالت قبل به صورت رشتهای و بر حسب پارامتر وارد میشوند. ورودی سوم نیز محدوده متغیر مستقل را مشخص میکند. برای مثال، فرض کنید بخواهیم نمودار منحنی توصیفشده با معادلات را در بازه رسم کنیم. برنامه زیر این کار را انجام میدهد:
1clc;
2clear;
3close all;
4%%
5figure(1);
6ezplot('t*sin(t)' , 't/2+cos(2*t)^2', [0 12*pi]) ; %#okشکل نمودار مطابق تصویر زیر است:
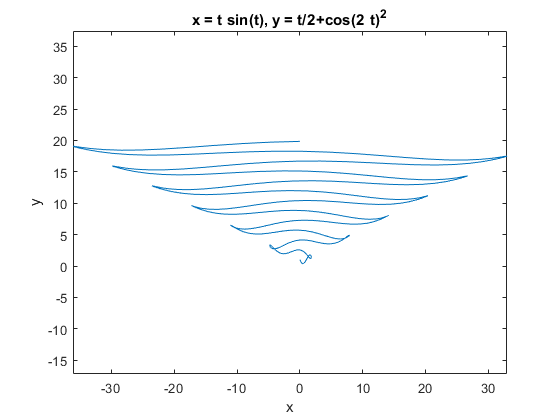 " width="560" height="420">
" width="560" height="420">علاوه بر رسم نمودار توابع صریح و پارامتری، میتوان نمودار توابع ضمنی را نیز توسط دستور ezplot رسم کرد. در این حالت فرمت وارد کردن اطلاعات به صورت زیر است:
ورودی یک رشته است که تابع را به فرم ضمنی بیان میکند. به عنوان مثال، میخواهیم نمودار تابع ضمنی را رسم کنیم. بازه تعریف متغیرها را 5- تا 5+ درنظر میگیریم. برنامه زیر رسم تابع ضمنی را انجام میدهد:
1clc;
2clear;
3close all;
4%%
5figure(1);
6ezplot('y*sin(x) + x*cos(y) - 1', [-5 5 -5 5]) ; %#okدر نهایت نمودار به شکل زیر رسم خواهد شد.
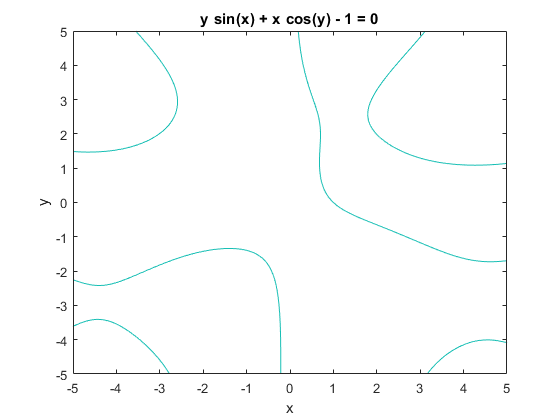 " width="560" height="420">
" width="560" height="420">رسم نمودار دو بعدی در متلب با دستور fplot
دستور پرکاربرد دیگر برای رسم نمودار دو بعدی در متلب ، دستور «fplot» است. در حالت اول، تابع مورد نظر به فرم سیمبولیک تعریف و با این دستور به صورت زیر رسم میشود.
ورودی دوم دستور fplot، بازه تغییرات متغیر مستقل است. دقت کنید اگر این ورودی به دستور داده نشود، برنامه به صورت پیش فرض بازه 5- تا 5+ را در نظر میگیرد. برای مثال برنامه زیر، تابع را توسط این دستور رسم میکند. دقت کنید که ابتدا متغیر به صورت سیمبولیک تعریف و سپس تابع مورد نظر بر حسب آن نوشته میشود.
1clc;
2clear;
3close all;
4%%
5figure(1);
6syms x
7f = sin(x)+sin(3*x)/3+sin(5*x)/5 ;
8fplot(f, [0 , 4*pi])با اجرای برنامه بالا رسم نمودار دو بعدی در متلب به صورت زیر انجام میپذیرد.
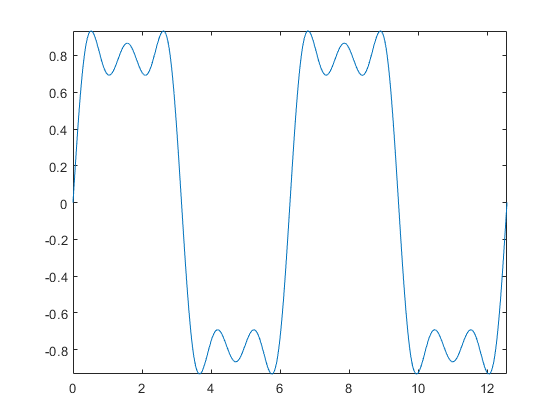 " width="560" height="420">
" width="560" height="420">بر اساس برنامه زیر تابع مورد نظر را میتوان به شکل Function-Handle نیز وارد کرد. با اجرای این برنامه نیز رسم نمودار دو بعدی در متلب انجام میشود و شکل بالا مجددا ترسیم خواهد شد.
1%%
2figure(1);
3f = @(x) sin(x)+sin(3*x)/3+sin(5*x)/5 ;
4fplot(f, [0 , 4*pi])با استفاده از دستور fplot میتوان توابع پارامتریک را نیز رسم کرد. نحوه استفاده از دستور به صورت زیر است:
در ابتدا، متغیر به فرم سیمبولیک تعریف میشود. سپس توابع و بر حسب نوشته میشوند. ورودی دوم دستور، بازه تغییرات متغیر مستقل است. برنامه زیر نمودار منحنی توصیف شده با معادلات را در بازه رسم میکند.
1clc;
2clear;
3close all;
4%%
5figure(1);
6syms t
7x = t*sin(t);
8y = t+cos(5*t)^2 ;
9fplot(x , y , [0 , 12*pi])نمودار به شکل زیر رسم میشود:
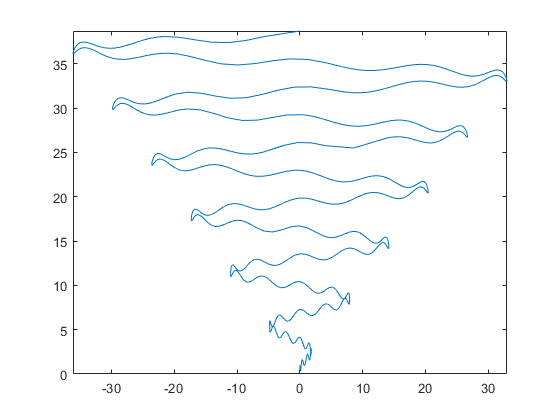 " width="560" height="420">
" width="560" height="420">رسم نمودار دو بعدی ضمنی با دستور fimplicit
با استفاده از دستور «fimplicit»، توابع ضمنی به شکل را میتوان رسم کرد. نحوه استفاده از این دستور به شکل زیر است:
تابع را میتوان هم به صورت Function-Handle و هم به صورت سیمبولیک وارد کرد. فرض کنید بخواهیم نمودار تابع ضمنی را رسم کنیم. برنامه زیر، به دو فرم مذکور تابع ضمنی را تعریف و رسم میکند.
1clc;
2clear;
3close all;
4%%
5figure(1);
6Function = @(x,y) y^2*cos(y)+x^2*sin(x)-1 ;
7fimplicit(Function, [-5 5 -5 5]*4);
8
9figure(2);
10syms x y
11Function = y^2*cos(y)+x^2*sin(x)-1 ;
12fimplicit(Function, [-5 5 -5 5]*4);نمودار به شکل زیر رسم خواهد شد.
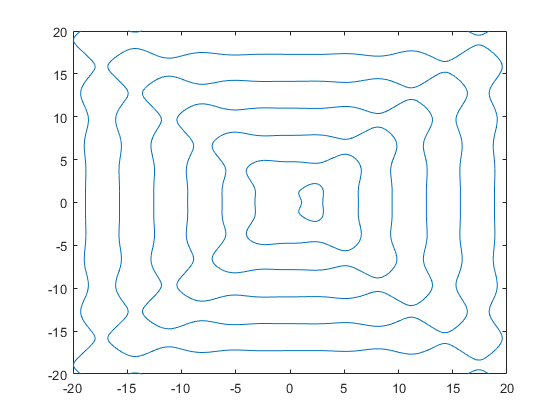 " width="560" height="420">
" width="560" height="420">رسم نمودار دو بعدی دلخواه با دستور plot
دستور «plot»، رایجترین دستور برای رسم نمودارهای دو بعدی است. فرض کنید دادههای و ، فقط در چند نقطه گسسته وجود داشته باشند. برای مثال، این دادهها میتوانند به فرم زیر باشند:
در این صورت، برای رسم بر حسب طبق دستور زیر پیش میرویم:
ورودی اول این دستور داده محور افقی و ورودی دوم آن داده محور عمودی را مشخص میکند. برنامه زیر نمودار بر حسب را برای دادههای بالا رسم میکند.
1clc;
2clear;
3close all;
4%%
5figure(1);
6x = [1 2 3 4 5 6 7];
7y = [0 0.5 5 2 5 0.5 0];
8plot(x , y) ;با اجرای برنامه بالا، نمودار به صورت شکل زیر رسم خواهد شد.
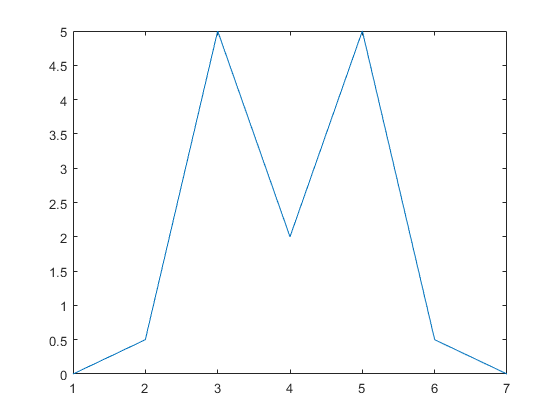 بر حسب " width="560" height="420">
بر حسب " width="560" height="420">حال فرض کنید بخواهیم نمودار تابع را با دستور plot رسم کنیم. ابتدا باید بازه تعریف متغیر مستقل را به تعداد زیادی بازه، با فاصلههای برابر تقسیمبندی کرد. سپس مقدار تابع در هر زیربازه باید محاسبه شود. در این صورت، یک بردار که همبعد با است به دست میآید. در نهایت با دستور fplot نمودار قابل رسم است. برنامه زیر این کار را انجام خواهد داد.
1clc;
2clear;
3close all;
4%%
5figure(1);
6x = 0:0.01:4*pi ;
7y = sin(x)+sin(3*x)/3+sin(5*x)/5 ;
8plot(x , y)با اجرای این برنامه دقیقا همان نموداری که قبلا با دستور ezplot رسم شد، ترسیم خواهد شد. لازم به ذکر است که این دستور در حقیقت نقاط متوالی را با یک خط به همدیگر متصل میکند.
زیباسازی رسم نمودار دو بعدی در متلب
در تمام دستوراتی که برای رسم نمودارهای دو بعدی ارائه شد، تنظیمات زیادی برای زیباسازی نمودار وجود دارد. در برنامه متلب زیر، مهمترین این دستورات ذکر شده است. فرض کنید، بخواهیم نمودار تابع مثال قبل را زیباسازی کنیم.
1clc;
2clear;
3close all;
4%%
5x = 0:0.1:4*pi ;
6y = sin(x)+sin(3*x)/3+sin(5*x)/5 ;
7
8figure1 = figure('Color',[0 1 1]);
9
10% Create axes
11axes1 = axes('Parent',figure1);
12hold(axes1,'on');
13
14% Create plot
15plot(x,y,'DisplayName','Y -X','MarkerFaceColor',[1 0 0],...
16 'MarkerEdgeColor',[1 0 0],...
17 'Marker','*',...
18 'LineWidth',2,...
19 'Color',[0 0 1]);
20
21% Create ylabel
22ylabel('Y (Meter)');
23
24% Create xlabel
25xlabel('X (Seconds)');
26
27% Create title
28title('FaraDars.Org');
29
30xlim(axes1,[0 12.5663706143592]);
31ylim(axes1,[-0.95 0.95]);
32box(axes1,'on');
33% Set the remaining axes properties
34set(axes1,'Color',[0.992156863212585 0.917647063732147 0.796078443527222],...
35 'FontSize',16,'XGrid','on','YGrid','on');
36% Create legend
37legend1 = legend(axes1,'show');
38set(legend1,...
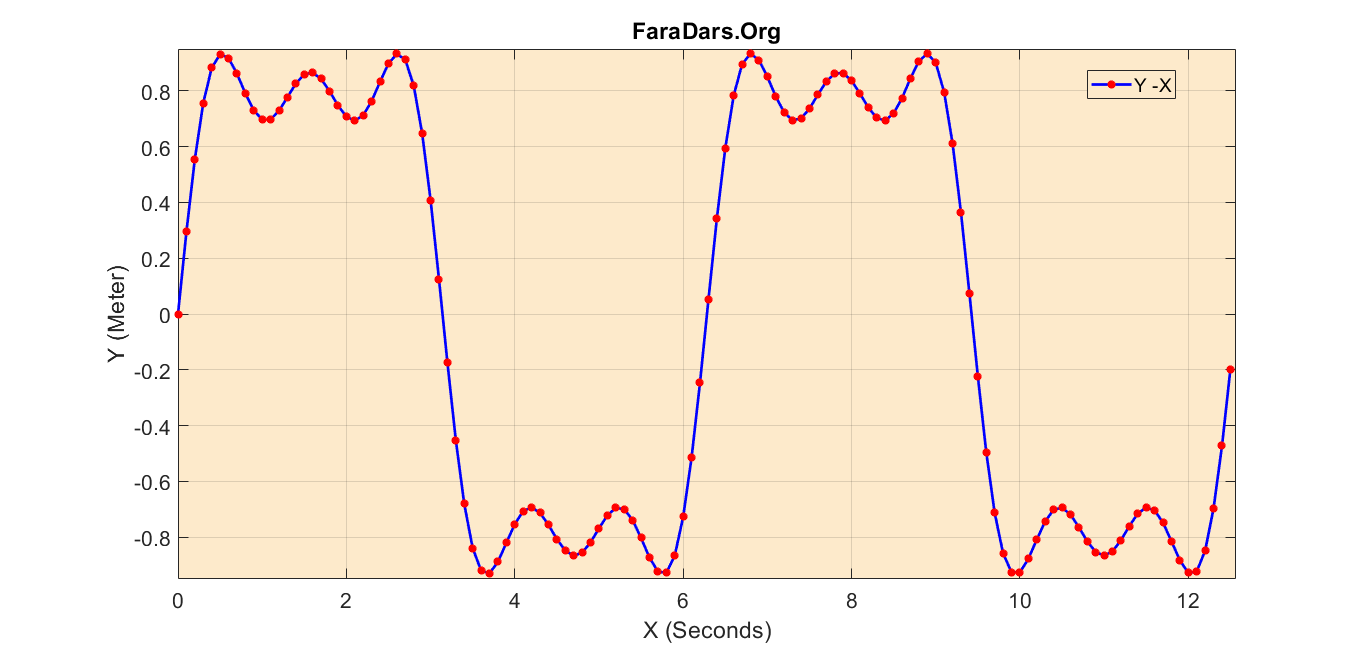
39 'Position',[0.795854528444928 0.845521998230901 0.0651537326994962 0.0480132437995727]);به صورت خلاصه، برنامه بالا را در ادامه توضیح میدهیم. خطوط 6 و 7 این برنامه، دادههای رسم را تعیین میکنند. در خط 9، یک پنجره برای رسم نمودار ایجاد خواهد شد که رنگ پسزمینه آن کرم است. در خط 18، نمودار همراه با یک سری تنظیمات رسم میشود. برای مثال مشخصه «DisplayName» لیبل نمودار را تعیین میکند. «Marker» باعث درج یک ستاره در هر نمونه متغیرهای نمودار میشود و «LineWidth» هم ضخامت نمودار را تنظیم میکند. در خطوط 26 ،30 و 34 عناوین محورهای افقی و عمودی و عنوان کل نمودار (متن بالای نمودار) درج میشوند. در نهایت، خطوط 36 و 37 محدوده نمایش محورهای افقی و عمودی را نشان میدهند.
با اجرای برنامه بالا، نمودار به صورت زیر رسم میشود. همان طور که مشاهده میکنید، نمودار از وضوح و خوانایی بیشتری برخوردار شده است. برای یادگیری بیشتر، تلاش کنید اعدادی و پارامترهای برنامه بالا را تغییر دهید و تاثیر آنها را در شکل نمودار مشاهده کنید.
رسم چند نمودار بر روی هم
برای رسم چندین نمودار بر روی یکدیگر، دو راه وجود دارد. در حالت اول، از ویژگی دستور plot استفاده میکنیم. با یک بار فراخوانی این دستور میتوان چندین نمودار را بر روی یکدیگر رسم کرد. شیوه این کار به صورت زیر است:
با اجرای این دستور، در یک پنجره نمودار بر حسب ، نمودار بر حسب ، نمودار بر حسب و الی آخر بر روی یکدیگر رسم میشوند.
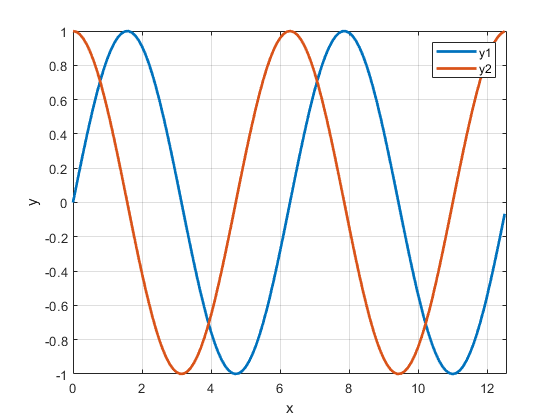
در حالت دوم، از دستور «hold on» استفاده میشود. توجه کنید که باید بعد از رسم نمودار اول، از این دستور استفاده کرد. در این صورت، نمودارهای بعدی، بر روی همین نمودار رسم خواهد شد. برای مثال، برنامه زیر توابع را در یک صفحه رسم میکند.
1%%
2x = 0:0.1:4*pi ;
3y1 = sin(x) ;
4y2 = cos(x) ;
5plot(x , y1 , 'LineWidth' , 2); hold on
6plot(x , y2 , 'LineWidth' , 2);
7xlabel('x');
8ylabel('y');
9legend('y1' , 'y2');
10grid on
11xlim([0 4*pi])بعد از اجرای برنامه، نمودار زیر رسم میشود.
رسم نمودار در زیر پنجرههای مختلف
گاهی لازم است چندین نمودار در یک پنجره (Figure)، اما نه بر روی همدیگر بلکه در زیرپنجرههای متفاوت رسم شوند. برای این کار، با استفاده از دستور «subplot» پنجره موردنظر را به چندین زیرپنجره تقسیمبندی میکنیم. سپس در زیرپنجرههای مختلف، نمودارهای مختلف را رسم میکنیم. برای مثال تابع زیر را درنظر بگیرید. این تابع در واقع سری فوریه موج مربعی است.
میخواهیم به ازای ، نمودار تابع را در زیرپنجرههای مختلف رسم کنیم. برنامه زیر این کار را انجام خواهد داد.
1clc;
2clear;
3close all;
4%%
5x = 0:0.1:4*pi ;
6for i = 1:3
7 figure(1);
8 subplot(3 , 1 , i);
9 y = 0 ;
10 for k = 1:i
11 y = y + sin((2*k-1)*x)/(2*k-1);
12 end
13 plot(x , y, 'LineWidth' , 2)
14 xlabel('x');
15 ylabel('y');
16 legend(['N = ' num2str(i)]);
17 grid on
18 xlim([0 4*pi])
19endبا اجرای این برنامه نمودار زیر رسم خواهد شد.
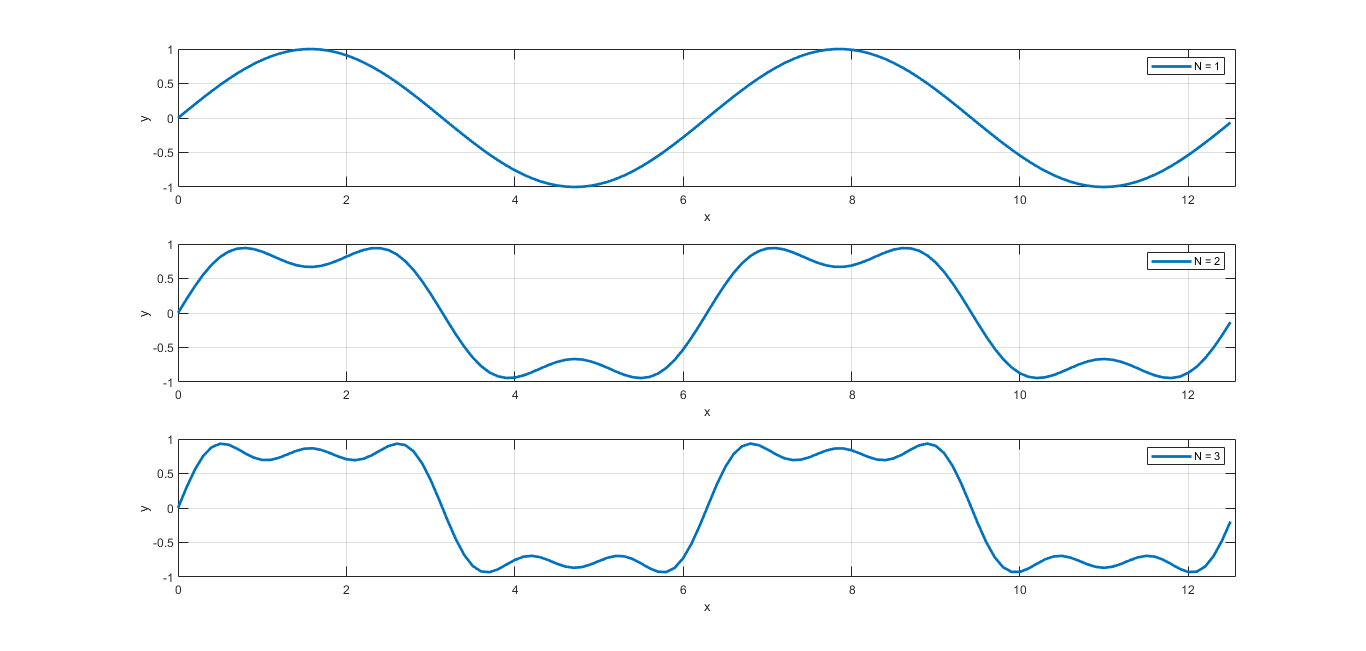
دقت کنید که ورودی اول دستور subplot، تعداد ردیفها، ورودی دوم تعداد ستونها و ورودی سوم آن شماره زیرپنجرهای را مشخص میکند که میخواهیم نمودار در آن رسم شود.
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزش های برنامه نویسی
- مجموعه آموزش های برنامهنویسی متلب (MATLAB)
- مجموعه آموزشهای پروژه محور برنامهنویسی
- مجموعه آموزش های برنامهنویسی متلب برای علوم و مهندسی
- منابع آموزشی نرم افزار متلب و برنامه نویسی کاربردی با آن
- تقلب نامه (Cheat Sheet) توابع و دستورات متلب (MATLAB)
- تقلب نامه (Cheat Sheet) تولباکس بهینه سازی در متلب — راهنمای کاربردی
^^













بسمه و تعالی
می خواهم با دستور fimplicite مجموع دو تابع با fipmlicit1,fimplicite2 را که با پارامترهای مختلف بدست امده
را ترسیم کنم ولی مشکل دارم.راهنمایی می خواهم
تشکر
با سلام
برای رسم معادله زیر چه مراحلی را طی نمود
y(t) =x(2t)
بسیار عالی و مفید ، سپاس فراوان
خیلی عالی خانم اقایی.ولی یه خواهش از شما دارم ،رسم نمودار از روی جدول 6تایی که تابع سینوس،کسینوس،رادیکال،eبه توان xوlnایکس و logایکس در بازه صفر تا ده راداشته باشه چه جوریه،اگه راهنمایی کنید خیلی ممنون میشم،متشکر
سلام.
برای این کار میتوانید از دستور subplot استفاده کنید که در بخش «رسم نمودار در زیر پنجرههای مختلف» همین مطلب به آن اشاره شده است.
سالم و موفق باشید.
خیلی مفید بود ممنون
سلام چطود میتونم این رو بدست بیارم لطفا کسی میتونع راهنمایی کنه انجامش بدم.
یک سیگنال sinc رو در متلب نمایش دهید و در پنجره جدید تبدیل فوریه همان سیگنال و اندازه آن را نمایش دهید به صورتی که سیگنال نمایش داده شده روی محور زمان از صفر تا ۲pi نمایش داده شود.
بسيار عالی، مختصر و مفید
ممنونم.