تحلیل چند متغیره در آمار — کاربردها و روش‌ها

در دنیای واقعی، بیان خصوصیات یک پدیده، متاثر از چندین ویژگی یا متغیر است که باید برای تحلیل، جمع‌آوری شوند. بنابراین اغلب با پدیده‌های چند متغیره مواجه هستیم. از آنجایی که بین این ویژگی‌ها ممکن است ارتباط نیز وجود داشته باشد، ریاضیات یا نظریه آماری که متکی به یک متغیر بوده یا متغیرها را مستقل از هم فرض می‌کند، کارایی نداشته و محاسبات ماتریسی و در نظر گرفتن ضرایب همبستگی بین متغیرها مورد استفاده قرار می‌گیرد. در این نوشتار از مجله فرادرس به موضوع تحلیل چند متغیره در آمار خواهیم پرداخت و جنبه‌های مختلف آن را مورد بررسی قرار می‌دهیم.

برای آشنایی با توزیع نرمال چند متغیره و تحلیل‌های آماری چند متغیره پیشنهاد می‌شود، مطالب دیگر مجله فرادرس مانند توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها و قضیه حد مرکزی و تعمیم آن — به زبان ساده را مطالعه کنید. همچنین خواندن نوشتارهای خانواده توزیع های پایدار — مفاهیم اولیه و تابع درست نمایی (Likelihood Function) و کاربردهای آن — به زبان ساده نیز خالی از لطف نیست.

تحلیل چند متغیره

«تحلیل چند متغیره» (Multivariate analysis) با به اختصار MVA، بر اساس اصول آمار چند متغیره ساخته شده است که مشاهده و تجزیه و تحلیل بیش از یک متغیر پاسخ را به طور همزمان در حوزه آمار، شامل می‌شود. به طور معمول، MVA برای پرداختن به مسئله‌هایی است که چندین اندازه‌گیری روی هر واحد آزمایشی صورت گرفته است و قرار است روابط بین این اندازه‌ها، تعیین و ساختارهای بین آن‌ها استخراج شود.

فیلم آموزش آنالیز داده های چند متغیره با نرم افزار Unscrambler X در فرادرس

کلیک کنید

یک شیوه طبقه‌بندی تحلیل چند متغیره در ادامه فهرست شده است:

• مدل‌های چند متغیره عادی و عمومی و نظریه توزیع
• مطالعه و اندازه گیری روابط وابستگی
• محاسبات احتمالات نقاط و مناطق چند بُعدی
• کاوش در ساختارها و الگوهای داده‌ها

تجزیه و تحلیل چند متغیره می‌تواند به صورت یک تحلیل پیچیده در آید. در این حالت متغیرها به صورت سلسله مراتبی با یکدیگر ارتباط داشته و مدل آماری باید به صورت آشیانه‌ای (Nested) ساخته و برآورد شود. از طرفی مواجه شدن با مسائل با «ابعاد بالا» (High Dimension) بر پیچیدگی مسئله می‌افزاید. در این مواقع، استفاده از تکنیک‌های کاهش بُعد در ساده‌سازی مسئله و انجام محاسبات در زمان حقیقی موثر هستند. همچنین دستیابی به مقادیر متغیرهای غیرقابل اندازه‌گیری و پنهان، یکی دیگر از تکنیک‌های چند متغیره محسوب می‌شود.

به منظور ساده‌سازی و ساخت یک مدل براساس شبیه‌سازی، از «روش مونت کارلو» (Monte Carlo Simulation) استفاده شده و نتایج حاصل از آن، برای ساخت مدل استفاده می‌شود. در این حالت شرایط قابل کنترل بوده و ویژگی‌ها، برای پدیده مورد نظر، قابل تعیین و اندازه‌گیری هستند.

کاربردهای روش‌های تحلیل چند متغیره در آمار نیز می‌تواند به صورت زیر فهرست شوند.

• آزمون فرض آماری چند متغیره (Multivariate hypothesis testing)
• کاهش ابعاد (Dimensionality reduction)
• کشف ساختار نهفته (Latent structure discovery)
• خوشه بندی (Clustering)
• تحلیل رگرسیون چند متغیره (Multivariate regression analysis)
• طبقه بندی و تجزیه و تحلیل ممیزی (Classification and discrimination analysis)
• انتخاب ویژگی (Variable or Feature selection)
• مقیاس گذاری چند بُعدی (Multidimensional Scaling)
• داده کاوی (Data mining)

آمار چند متغیره

آمار چند متغیره بخشی از «نظریه آمار» (Statistical Theory) است که شامل مشاهده و تجزیه و تحلیل همزمان بیش از یک متغیر پاسخ است. کاربرد آمار چند متغیره در «تحلیل چند متغیره» (Multivariate Analysis) یا به اختصار MVA، به چشم می‌خورد.

فیلم آموزش آماده سازی داده ها در اس پی اس اس SPSS برای تحلیل آماری در فرادرس

کلیک کنید

همانطور که گفته شد، آمار و تحلیل چند متغیره مربوط به درک رفتار و عملکرد مختلف هر یک از ویژگی‌های متغیر پاسخ می‌پردازد و نحوه ارتباط آنها با یکدیگر را تعیین می‌کند. به این ترتیب خصوصیات و «همبستگی» (Correlation) بین هر یک از ابعاد «متغیر وابسته» (Dependent Variable) نسبت به متغیر یا «متغیرهای مستقل» (Independent Variables) مورد تحلیل قرار می‌گیرد. کاربرد عملی آمار چند متغیره برای یک مسئله خاص ممکن است شامل چندین نوع تحلیل تک متغیره و چند متغیره به منظور درک روابط بین متغیرها و ارتباط آنها با مسئله مورد مطالعه باشد. به علاوه، آمار چند متغیره از نظر هر دو منظر (تحلیل تک متغیره و چند متغیره)، ارتباط تنگاتنگی با توزیع احتمالات جامعه آماری دارد که می‌تواند به موارد زیر در این رابطه پاسخ دهد.

• چگونه می توان از آمار و تحلیل چند متغیره برای نمایش توزیع داده‌های مشاهده شده استفاده کرد؟
• چگونه می‌توان از تحلیل چند متغیره به عنوان بخشی از استنباط آماری بهره برد، خصوصاً در مواردی که چندین مقدار مختلف به طور همزمان مورد توجه هستند؟

در این بین می‌توان به مسائلی مانند رگرسیون خطی ساده و رگرسیون چندگانه، اشاره کرد که در آن، تحلیل چند متغیره مورد استفاده قرار می‌گیرد. البته موارد خاصی نیز وجود دارد که در تحلیل رگرسیونی، از آمار چند متغیره برای تحلیل استفاده نمی‌شود، زیرا با در نظر گرفتن توزیع شرطی (یک متغیره) ، متغیر پاسخ به صورت تک متغیره در آمده و با توجه به ویژگی‌های آن، مسئله مورد تجزیه و تحلیل قرار می‌گیرد. همچنین به کمک تکنیک‌های انتخاب ویژگی می‌توان از ابعاد یک مسئله پیچیده کاست.

انواع تجزیه و تحلیل

مدلهای مختلفی وجود دارد که هر کدام نوع تجزیه و تحلیل خاص خود را دارند. به فهرست ارائه در ادامه متن توجه کنید.

• تحلیل واریانس چند متغیره (MANOVA): تجزیه و تحلیل واریانس چند متغیره همان حالت گسترش یافته آنالیز واریانس محسوب می‌شود. به این ترتیب اگر مشاهدات وابسته دارای چند متغیر باشند، «تحلیل واریانس چند متغیره» (Multivariate analysis of variance) قادر است میانگین بین گروه‌های تولید شده توسط متغیر مستقل را در بین این چند متغیره بسنجند. مسائل و مواردی که بیش از یک متغیر وابسته برای تجزیه و تحلیل همزمان دارند، توسط MANOVA پوشش داده می‌شود. همچنین «تحلیل چند متغیره کوواریانس» (Multivariate analysis of covariance) که به اختصار MANCOVA نامیده می‌شود، در مجموعه تحلیل واریانس چند متغیره قرار می‌گیرد.
• تحلیل رگرسیون چند متغیره (Multivariate Regression): رگرسیون چند متغیره سعی در ارائه فرمولی دارد که توسط آن بتوان، چگونگی واکنش مولفه‌های بردار متغیرهای وابسته را به طور همزمان نسبت به تغییرات متغیرهای توصیفی، بیان کرد. برای روابط خطی، تحلیل رگرسیون در اینجا بر اساس شکل‌های مختلف «مدل خطی عمومی» (General Linear Model) ساخته می‌شود. به یاد داشته باشید که «رگرسیون چندگانه» (Multiple Regression) با رگرسیون چند متغیره تفاوت دارد. در رگرسیون چندگانه تعداد متغیرها توصیفی یا پیشگو که نقش متغیر مستقل را بازی می‌کنند، بیش از یکی است در حالیکه در رگرسیون چند متغیره، مشاهدات مربوط به داده‌های پاسخ به صورت چند متغیره هستند در حالیکه ممکن است متغیر مستقل به یک متغیر محدود شود.
• تجزیه و تحلیل مولفه‌های اصلی (PCA): یکی دیگر از کاربردهای آمار چند متغیره، «تجزیه و تحلیل مولفه‌های اصلی» (Principal components analysis) است. این روش مجموعه جدیدی از متغیرهای متعامد را ایجاد می‌کند که حاوی همان اطلاعات مجموعه اصلی است. با این کار محورهای مختصات مربوط به داده‌ها چرخانده شده و مجموعه جدیدی از محورهای متعامد تشکیل می‌شود که تعداد آن‌ها به گونه‌ای است که نسبت به حالت عادی، متغیرهای کمتر و محورهای کمتری را شامل شده، بطوری که تقریبا پراکندگی همه نقاط را نشان می‌دهد.
• تجزیه و تحلیل عامل‌ها (Factor Analysis): تحلیل عاملی یا فاکتورها مشابه PCA عمل می‌کند اما به کاربر اجازه می‌دهد تعداد مشخصی از متغیرهای مصنوعی که مسلما کمتر از مجموعه اصلی هستند را استخراج کند و باقی مانده غیرقابل توصیف را به عنوان خطا باقی بگذارد. متغیرهای استخراج شده به عنوان متغیرهای پنهان (Latent Variable) یا عوامل، شناخته می‌شوند. ممکن است هرکدام از این متغیرها به عنوان متغیر مزاحم نسبت به متغیرهای عادی یا مشاهده شده در نظر گرفته شوند.
• تجزیه و تحلیل همبستگی کانونی (Canonical correlation analysis): روابط خطی بین دو مجموعه متغیر توسط تجزیه و تحلیل همیستگی کانونی مورد ارزیابی قرار می‌گیرد. این روش، نسخه تعمیم یافته «همبستگی دو متغیره» (Bivariate Correlation) محسوب می‌شود.
• تجزیه و تحلیل افزونگی (RDA): یکی از تکنیک‌های چند متغیره، «تجزیه و تحلیل افزونگی» (Redundancy analysis) است که مشابه تجزیه و تحلیل همبستگی کانونی عمل می‌کند، اما به کاربر اجازه می‌دهد تعداد مشخصی از متغیرهای ساختگی را از یک مجموعه متغیر (مستقل) استخراج کرده بطوری که تا آنجا که ممکن است واریانس را نسبت به مجموعه دیگری از متغیر مستقل، توضیح دهد. این تحلیل مشابه رگرسیون چند متغیره است.
• تجزیه و تحلیل تناظری (CA): در «تجزیه و تحلیل تناظری» (Correspondence analysis) درست به مانند روش PCA، مجموعه‌ای از متغیرهای مصنوعی جستجو شده که مجموعه اصلی را خلاصه می‌کنند. مدل اساسی فرضیه براساس مقدار «آماره کای دو» (Chi Square) ‌و  شباهت مبتنی بر آن استوار است.
• تحلیل کانونی تناظری (CCA): اگر تغییرات یا پراکندگی بین متغیرها را به دو بخش مشترک و غیر مشترک تفکیک کنیم، به نوعی از «تحلیل کانونی تناظری» (Canonical Correspondence Analysis) استفاده کرد‌ه‌ایم. تحلیل CCA را می‌توان ترکیبی از تحلیل تناظری و تحلیل رگرسیون چند متغیره در نظر گرفت. مدل اساسی در این روش استفاده از «میزان عدم شباهت کای ۲» (Chi Square Dissimilarity) در بین مشاهدات است.
• مقیاس گذاری چند بُعدی (Multidimensional scaling): این تکنیک شامل الگوریتم‌های مختلفی برای تعیین مجموعه‌ای از متغیرهای مصنوعی است که فاصله دوتایی بین آن‌ّها را به بهترین شکل نشان می‌دهد. روش اصلی در اینجا، «تجزیه و تحلیل مختصات اصلی» (Principal Coordinates Analysis)‌ است.
• تحلیل ممیزی (Discriminant analysis): تحلیل ممیزی یا «تحلیل متغیر کانونی» (Canonical Variate Analysis)، تلاش می‌کند مجموعه‌ای از متغیرها برای تمایز بین دو یا چند گروه را تشخیص داده و برای جداسازی به کار برد.
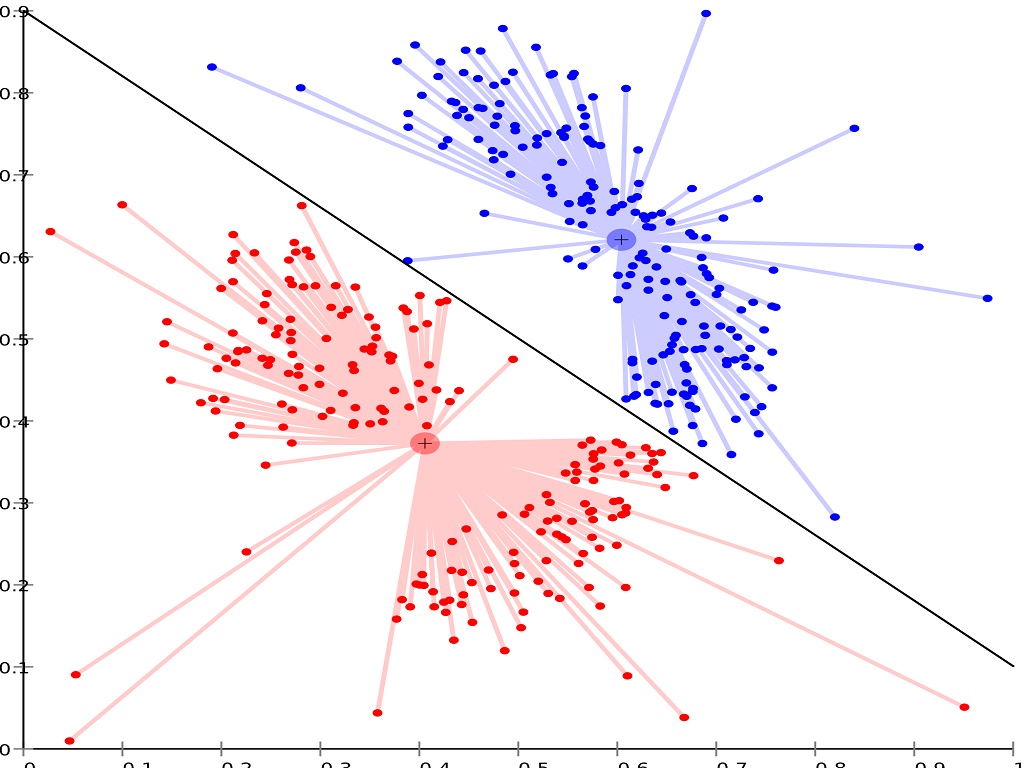
• تجزیه و تحلیل ممیز خطی (LDA): یکی از شاخه‌ّای تحلیل ممیزی، «تجزیه و تحلیل ممیز خطی» (Linear discriminant analysis) است که بوسیله یک مدل خطی، دو مجموعه داده با توزیع نرمال را از یکدیگر تشخیص می‌دهد. این تکنیک برای طبقه‌بندی یا دسته‌بندی داده‌ها براساس یک مدل ساخته شده بوسیله داده‌های قبلی به کار می‌رود.
• تحلیل خوشه‌بندی (Clustering): سیستم‌های خوشه‌بندی اشیا را به گروه‌هایی تقسیم می‌کنند که هر یک از آن‌ها را خوشه می‌نامیم. خوشه‌ها به گونه‌ای تشکیل می‌شوند که اعضای هر خوشه با هم نوعان خود در همان خوشه  بیشترین شباهت را داشته و در مقابل با خوشه‌های دیگر کمترین شباهت را داشته باشند.
• پارتیشن‌بندی بازگشتی (Recursive partitioning): یک درخت تصمیم باینری یا دو دویی را در نظر بگیرید که به کمک آن طبقه یا گروه‌ها تعیین می‌شوند. براساس این درخت، گروه‌بندی و تفکیک اعضای جامعه به صورت سلسله مراتبی صورت گرفته و به نوعی گروه‌های همسان تشخیص داده می‌شوند. چنین روشی را به پارتیشن‌بندی بازگشتی یا تفکیک بازگشتی می‌شناسیم.
• شبکه‌های عصبی مصنوعی (ANN): روش‌های رگرسیون و خوشه‌بندی در «شبکه‌های عصبی مصنوعی» (Artificial Neural Network) به یکدیگر پیوند خورده و مدل‌های چند متغیره غیر خطی را گسترش می‌دهند که در شبکه‌های عصبی مصنوعی به کار می‌روند.
• نمودارهای آماری (Statistical graphics): برای کشف ارتباط بین داده‌های چند متغیره می‌توان از گرافیک های آماری مانند «نمودارهای مختصات موازی» (Parallel Coordinate Plots) و «ماتریس‌های پراکندگی» (Scatterplot Matrices) استفاده کرد.
• مدل‌های معادلات همزمان (Simultaneous Equations Models): این تحلیل شامل بیش از یک معادله رگرسیون، با متغیرهای مختلف وابسته است که پارامترهای آن به کمک داده‌های جمع‌آوری شده برآورد می‌شوند.
• اتورگرسیون برداری (Vector Autoregression): اتورگرسیو برداری، شامل رگرسیون همزمان متغیرهای مختلف، سری زمانی با مدل AR و مقادیر تأخیر است. واضح است که هر یک از متغیرها بر یکدیگر نیز اثر گذارند.
• تجزیه و تحلیل منحنی پاسخ اصلی (PRC): یکی از روش‌هایی که بر تجزیه و تحلیل افزونگی (RDA) متکی  است تجزیه و تحلیل «منحنی پاسخ اصلی» (Principal Response Curves) است. این تکنیک به کاربر اجازه می‌دهد با اصلاح تغییرات در تیمارها و گروه کنترل به مرور زمان، اثرات تیمارها و اختلاف‌ها را مشخص کند.

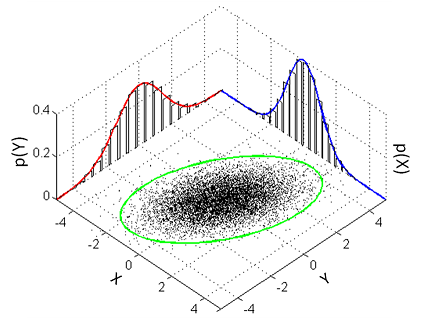
توزیع احتمال مهم در تحلیل چند متغیره

مجموعه‌ای از توزیع‌های احتمالی که در تحلیل‌های چند متغیره نقش اساسی دارند در ادامه فهرست شده‌اند. توجه به خصوصیات هر یک از پدیده‌های چند متغیره در انتخاب درست توزیع مورد نظر نقش دارد. بنابراین شاخت این توزیع‌ها نیز ضروری به نظر می‌رسد.

• توزیع نرمال چند متغیره (Multivariate Normal Distribution)
• توزیع ویشارت (Wishart Distribution)
• توزیع چند متغیره Student-t

فیلم آموزش آمار و احتمال مهندسی – جامع و با مثال های مختلف در فرادرس

کلیک کنید

توزیع معکوس ویشارت در استنباط بیزی، به عنوان مثال در رگرسیون خطی چند متغیره بیزی مهم است. علاوه بر این، توزیع مربع T Hotelling یک توزیع چند متغیره است، و توزیع t را تعمیم می‌دهد که در تست فرضیه چند متغیره استفاده می‌شود.

تاریخچه

کتاب درسی اندرسون در سال 1958 با نام «مقدمه ای بر تحلیل چند متغیره» (An Introduction to Multivariate Statistical Analysis)، نسلی از نظریه پردازان و آمار شناسان کاربردی را آموزش داد. کتاب اندرسون بر آزمون فرض از طریق نسبت درست نمایی و خواص توابع توان، تأکید دارد. همچنین در این کتاب مباحث مربوط به «قابل قبول بودن» (Admissibility)‌، بی طرفی و «نااریبی»(Unbiasedness) و «یکنواختی» (Monotonicity) برای برآوردگرها پرداخته شده است.

نرم افزار و ابزارها

تعداد زیادی بسته نرم افزاری و سایر ابزارها برای تجزیه و تحلیل چند متغیره وجود دارد. فهرست زیر به بعضی از این بسته‌ها اشاره کرده است.

• JMP (بسته نرم‌افزار آماری)
• MiniTab (بسته نرم‌افزار آماری)
• Calc (بسته نرم‌افزار آماری)
• PSPP (بسته نرم‌افزار آماری)
• R (زبان برنامه‌نویسی)
• SAS (بسته نرم افزار)
• SciPy کتابخانه‌ای برای پایتون
• SPSS (بسته نرم‌افزار آماری)
• STATA (بسته نرم‌افزار آماری)
• STATISTICA (بسته نرم‌افزار آماری)
• Unscrambler (بسته نرم‌افزار آماری)
• WarpPLS (بسته نرم‌افزار آماری)
• SmartPLS (بسته نرم‌افزار آماری)
• MATLAB (زبان برنامه‌نویسی)
• Eviews (بسته نرم‌افزار آماری)

خلاصه و جمع‌بندی

در این نوشتار با مفهوم و روش‌های تحلیل داده‌های چند متغیره و تکنیک‌های آماری متناسب با آن‌ها آشنا شده و شاخه آمار چند متغیره را شناختیم. از آنجایی که ماتریس‌ها برای بیان چنین داده‌هایی بسیار به کار می روند، آگاهی از جبر خطی و محاسبات ماتریسی در تجزیه و تحلیل چند متغیره اهمیت زیادی دارد. در این متن چند توزیع مهم که به صورت چند متغیره بوده یا تعمیمی از حالت تک متغیره توزیع‌های خاص هستند، نیز معرفی شدند. همچنین نرم‌افزارهایی که برای انجام تحقیق در زمینه یا حوزه چند متغیره قابل استفاده هستند نیز به صورت یک لیست یادآوری شدند. اغلب تحلیل‌های چند متغیره به مانند تحلیل تک متغیره بوده ولی بیشتر تجزیه و تحلیل‌های چند متغیره از محاسبات ماتریسی برای نمایش یا انجام عملیات ریاضی بهره می‌برند.