تقریب لاپلاس تو در تو یکپارچه — به زبان ساده
الگوریتم یا تکنیک تقریب لاپلاس تو در تو یکپارچه یا (INLA) یک جایگزین خوب و البته سریع برای الگوریتم MCMC یا «زنجیره مارکف مونت کارلو» (Mont Carlo Markov Chain) برای «مدلهای بیزی» (Bayesian Models) است. واضح است که هر کدام از این دو روش، موارد مثبت و منفی خاص خود را دارند، اما در حالی که MCMC روشی بسیار بصری بوده و برای یادگیری و حتی اجرا روی سناریوهای مختلف، ساده است، الگوریتمهای «تقریب لاپلاس تو در تو یکپارچه» (Integrated Nested Laplace Approximation) یا INLA کاراتر و سریعتر عمل میکنند.
این متن به طور خلاصهای از قابلیتها در تکنیک یا الگوریتم INLA پرده بر میدارد و بخصوص برای کسانی که مقداری آشنایی با آمار کاربردی و نظریه توزیعها مثل توزیع نرمال و همچنین «قضیه بیز» (Bayesian Theorem) دارند مفید است. همچنین آگاهی خوانندگان از مفاهیمی ریاضیات مانند بسطها یا «سریهای تیلور» (Tailor Series) نیز ضروری است.
تقریب لاپلاس تو در تو یکپارچه INLA
مدلهای سلسله مراتبی به طور گستردهای در حوزههای مطالعاتی بین رشتهای مورد استفاده قرار میگیرند تا ساختارهای پیچیده وابستگی در دادهها را نشان دهند. عدم قطعیت و تصادفی بودن در برآوردگرهای پارامترهای مدل و متغیرها را میتوان با بهرهگیری از نظریه بیز و «توزیعهای پیشین» (Prior Distribution) مناسب، در چارچوب بیزی به کار بست.
در حالی که تقریباً هیچ راه حل بسته و قطعی برای انتخاب توزیع پیشین وجود ندارد؛ راه حلهای کلی از طریق روشهای «مونت کارلو با زنجیره مارکوف» (MCMC) توسط نرمافزارهایی مانند WinBUGS مورد استفاده قرار گرفتهاند. البته تکنیک MCMC به آهستگی عمل کرده و به خوبی مقیاسپذیر نیست و برای برخی از مدلهای پیچیده ممکن است همگرا نبوده و در تشکیل مدل شکست بخورد. نرم افزارهای جدیدتر (JAGS، Stan) سعی در برطرف کردن این چالشها در الگوریتم MCMC دارند.
MCMC یک روش دقیق محسوب میشود در حالی که INLA یک تکنیک تقریبی است. گاهی اوقات استفاده از INLA با سوء ظن یا سؤالاتی مواجه میشد. این سوالات ممکن است به صورت «خطای تقریبی چقدر است؟» یا «چقدر به نتایج خود اطمینان دارید؟» ظاهر شوند که ممکن است نتوان به آنها جواب دقیقی داد. ولی آنچه مهم است کارایی این تکنیک در انجام سریع محاسبات است. در انتهای این متن مقایسهای از دقت مربوط به INLA و روش MCMC صورت خواهد گرفت.
مواقعی وجود دارد که INLA نیز با شکست مواجه میشود، اما خوب است به یاد داشته باشید که در بیشتر اوقات شرایط مسئله در حالت ایدهآل (مشخص بودن توزیع یا عدم نقاط پرت) مطرح نمیشود. از نظر تجربی و توسط بسیاری از مطالعات شبیهسازی، نشان داده شده است که خطای MCMC و خطای INLA غالباً بسیار نزدیک به هم هستند و نتایج یکسانی تولید میکنند.
INLA یا همان تقریب لاپلاس تو در تو ، یک جایگزین سریع برای MCMC برای کلاس عمومی مدلهای پنهان گاوسی (LGM) است. بسیاری از مدلهای آشنا را میتوان دوباره در INLA مورد استفاده قرار داد. برای مثال مدل خطی عمومی (General Linear Model) که به اختصار GLM نامیده میشود و همینطور «مدل جمعی عمومی» (General Additive Model) که به اختصار به صورت GAM نوشته میشود از مواردی هستند که INLA در آنها قابل استفاده است. همچنین «سریزمانی» (Time Series)، «مدلهای فضایی» (Spatial Models)، «مدلهای خطای اندازهگیری» (Measurement Error Models) و موارد دیگر نیز توسط INLA تقریب زده میشوند.
مهمترین کاربردهای روش معروف به INLA در ادامه به صورت یک فهرست بیان شدهاند.
- استنتاج بیزی (Bayesian Inference)
- مدلهای پنهان گاوسی (Latent Gaussian Model) یا LGM
- فیلدهای تصادفی Gaussian Markov Random Fields یا (GMRFs)
- تقریبهای لاپلاس (Laplace Approximation)
در ادامه این نوشتار فرض میکنیم که با «استنباط بیزی» (Bayesian inference) و نظریه توزیعهای آماری (Distribution Theory) آشنایی داشته و به بعضی از مفاهیم اولیه مانند روشهای عددی و الگوریتم MCMC نیز تا حدودی مسلط هستید.
استنتاج بیزی
در یک مدل بیزی، ما به طور کلی توزیع توزیع خلفی را برای مدلهای خود می خواهیم (به عنوان مثال ، توزیع پارامترهای داده داده شده) یا توزیع خلفی پیش بینی شده (برای پیش بینی / پیش بینی - توزیع مقادیر جدید با توجه به موارد مشاهده شده). بیایید به پرونده قبلی توجه کنیم، مورد دوم منطقی است.
طبق نظریه و استنباط بیزی میدانیم که توزیع پسین برابر است با حاصل ضرب احتمال تابع درستنمایی (Likelihood Function) برحسب مقادیر دادهها در توزیع پیشین. به منظور نرمالسازی، این حاصل ضرب را به مجموع یا انتگرال این حاصل ضرب تقسیم میکنیم تا توزیع پسین بدست آمده دارای انتگرال یک روی مجموعه مقادیر پارامتر باشد.
$$ \large p(\mathbf{\theta} | \mathbf{y}) = \frac{p(\mathbf{y|\theta}) p(\mathbf{\theta})} {\int p(\mathbf{y|\theta}) p(\mathbf{\theta})d\mathbf{\theta}} \propto p(\mathbf{y|\theta}) p(\mathbf{\theta}) $$
اگر در چارچوب فراوانیگرا به مسئله نگاه کنیم، اغلب با استفاده از روشهای عددی مانند تکنیک «نیوتن-رافسون» (Newton-Raphosn)، حداکثر تابع درستنمایی (Likelihood Function) را به دست میآوریم تا برای یک پارامتر معین (که ما آن را ثابت اما ناشناخته میدانیم) برآورد نقطهی بدست آید. همچنین از همین ایده به شکلی دیگر برای تخمین فاصله اطمینان متناظر استفاده میشود.
از طرفی، اغلب میتوان از یک روش ساده و آسان مثل «باز نمونهگیری» (Resampling) در «بوت استرپ» (Bootstraping)، برای محاسبه توزیع برآوردگرها یا پارامترهای توزیع آنها استفاده کرد ولی در اینجا منظور ما چیزی دیگری است.
در یک تجزیه و تحلیل بیزی ما یک «توزیع پیشین» (Prior Distribution) برای پارامتر (که ما آن را به عنوان یک متغیر تصادفی مشاهده می کنیم) در نظر میگیریم و براساس آن توزیع پسین را مشخص کرده، که برای آن میتوانیم شاخصهای آماری (مانند میانگین، میانه و نما) و مقادیری را ارائه دهیم تا مستقیماً برآوردگرها یا فواصل اطمینان را بدست آوریم.
اگر برای هر پارامتر از توزیعهای «پیشین مزدوج» (Conjugate Priors) استفاده کنیم، ممکن است بتوانیم توزیع پسین را به فرم بسته تعیین کنیم. به طور کلی، محاسبه انتگرال در مخرج کسر بالا، بسیار سخت و گاهی به شیوه صریح قابل تعیین نیست، بنابراین ما از روشهای عددی مانند MCMC استفاده کرده و با نمونهگیری از شرایط موجود در مسئله استفاده کرده و توزیع حاشیهای را برای هر پارامتر مورد نظر تخمین میزنیم تا انتگرال مخرج را مورد محاسبه قرار دهیم.
مدل های پنهان گاوسی
فرم کلی برای LGM به بخشهای زیر وابسته است.
- تابع درستنمایی (Likelihood Function):
$$ \large \mathbf{y} | \mathbf{x}, \mathbf{ \theta_2} \sim \prod_i \ p(y_i | \eta_i, \mathbf{ \theta_2}) $$
- فیلد پنهان (Latent Field):
$$ \large \mathbf{x} | \mathbf{ \theta_1} \sim p( \mathbf{x}|\mathbf{\theta_1}) = \mathcal{N} (0,\mathbf{\Sigma})$$
- اَبَر پارامتر پیشین (HyperPriors):
$$ \large \mathbf{{ \theta}} = [\mathbf{\theta_1},\mathbf{\theta_2}]^T \sim p(\mathbf{\theta}) $$
در رابطه بالا $$y$$ مشاهدات را تشکیل میدهند و همچنین $$x$$ نیز متغیر پنهان محسوب شده ولی با $$y$$ وابستگی (Covariate) ندارند. از طرفی توزیع توام آنها با پارامترهای مشخص تعیین شده و نرمال در نظر گرفته شده است. در انتها نیز اَبَر پارامتر برای میدان پنهان ($$x$$) قرار گرفته که دارای توزیع گاوسی نیست.
سوال اصلی این است چگونه میتوان یک مدل GLM را به چنین مسئلهای برازش کرد؟ در حقیقت هدف برآورد پارامترهای این مدل یعنی $$\Sigma$$ و $$\eta$$ و همچنین $$\theta_1$$ و $$\theta_2$$ است. در این متن در حالت ساده یک فرم عمومی برای GAM و GLM به شکل زیر در نظر میگیریم.
$$ \large \mathbf{y} \sim \prod_i^N p(y_i | \mu_i) $$
$$ \large g(\mu_i) = \eta_i = \alpha + \sum_{k = 1}^{n_\beta} \beta_k z_{ki} + \sum_{j = 1}^{n_f} f^{(j)}(w_{ji}) + \varepsilon_i $$
در رابطه بالا منظور از $$g(\cdot)$$ یک «تابع پیوند» (Link Function) محسوب میشود. همچنین $$\alpha$$ نیز عرض از مبدا و $$\beta$$ پارامتر رگرسیون خطی همبسته با $$z$$ است. همچنین $$f = f_1(\cdot),f_2(\cdot) , \ldots , f_{n\beta}(\cdot)$$ مجموعهای از توابع هستند که مرتبط با $$w$$ ولی به شکل غیرخطی هستند. این ارتباط میتواند براساس اثرات نمونههای گیری تصادفی و همتوزیعی (iid) یا اثرات همبستگی فضایی، یا هموارسازی spline باشد.
رگرسیون خطی یک حالت خاص از این موضوع یا مدل محسوب میشود که در آن نتایج متغیر پاسخ، دارای توزیع گاوسی (نرمال) هستند. در این حالت «تابع پیوند» (Link Function) یک تابع ثابت مثل $$f(\cdot) = 0 $$ است. در مدل کلاسیک فضایی نیز داریم:
$$ \large f_1(\cdot)\; \sim\;CAR ,\;\;\; f_2(\cdot) \; \sim \; N(0 , \sigma^2_{f_2}) $$
در مواردی که نتایج مدل رگرسیونی به صورت مقادیری با «توزیع دو جملهای» (Binomial Distribution) یا «توزیع پواسن» (Poisson Distribution) هستند، اغلب تابع پیوند را به صورت یک «تابع لوجیت» (Logit Function) یا لگاریتم آن در نظر میگیرند. چنین مدلهایی ریشه و اصل مدلهای دیگر در این زمینه را تشکیل میدهند. در حقیقت مدلهای دیگر حالتهای خاصی از این مدلها محسوب میشوند.
مدل گوسی پنهان (Latent Gaussian Model)، در حقیقت شبیه یک مدل LGM یا مدل خطی گاوسی (Linear Gaussian Model) است، اگر پارامترهای آن دارای توزیع توام گاوسی باشند. به این ترتیب بهتر است یک توزیع پیشین نرمال برای پارامترها در حالت استنباط بیزی برایشان در نظر بگیریم.
$$ \large \mathbf{x} = [\mathbf{\eta}, \alpha, \mathbf{\beta}, \mathbf{f}(\cdot)] \sim \mathcal{N}(0, \mathbf{\Sigma})$$
البته اگر استقلال شرطی نیز در نظر گرفته شود، میدان پنهان $$x$$ تشکیل یک میدان تصادفی گاوسی مارکف خواهد داد. این شرط چندان هم دور از دسترس نیست. در مورد این موضوع در بخشهای بعدی بحث خواهیم کرد. توجه داشته باشید که بُعد $$x$$ بسیار بزرگ است ولی بُعد پارامتر غیرگاوسی $$\theta$$ در حالت عمومی کمتر است. در نتیجه همین ویژگی ما را به سوی INLA سوق میدهد. پس بهتر است بحث را ادامه داده تا به مدل INLA برسیم.
میدانهای تصادفی گاوسی مارکف
یک «میدان گوسی مارکف» (Gaussian Markov Random Field) که به اختصار GMRF گفته میشود، برداری تصادفی با توزیع چند متغیره نرمال است که دارای خاصیت مارکفی است. برای مثال $$x_i \bot x_j | X_{-ij} , \;\;\; i \neq j $$ یک میدان گاوسی مارکفی است. توجه داشته باشید که نماد $$-ij$$ نشانگر عناصر است که شامل $$i , j $$ نمیشوند.
توجه داشته باشید که یک فرایند خودهمبسته (Autoregressive) از نوع زمانی یا مکانی را میتوان به صورت یک میدان تصادفی گاوسی مارکف در نظر گرفت.
میدانیم که دقت (Precision) به نوعی معکوس واریانس محسوب میشود. به همین ترتیب اگر ماتریس $$Q$$ را به صورت معکوس ماتریس کوواریانس $$\Sigma$$ محسوب کنیم میتوانیم رابطه زیر را بنویسیم.
$$ \large X \sim N(0 , Q^{-1} ) , \;\; Q = \Sigma^{-1} $$
متاسفانه محاسبه معکوس یک ماتریس، بار محاسباتی زیادی دارد و به سادگی قابل اجرا نیست. درجه پیچیدگی محاسباتی برای معکوس ماتریس به صورت $$O(n^3)$$ است. البته توجه داشته باشید که «ماتریسهای خلوت» (Sparse Matrix) که شامل عناصر زیادی به صورت صفر هستند، از این قاعده مستثنی میشوند. برای مثال یک ماتریس قطری (Diagonal Matrix) مثل $$D$$ را در نظر بگیرید، چنین ماتریسی یک ماتریس خلوت محسوب میشود. معکوس چنین ماتریسی، یک ماتریس هم بُعد ولی با درایههای معکوس است.
$$ \large D = [d_{ij}] , \;\;\; D^{-1} = [\dfrac{1}{d_{ij}}] $$
به این ترتیب معکوس «ماتریس همانی» (Identity Matrix) نیز ماتریس همانی خواهد بود.
$$ \large I^{-1} = I $$
نکته: این موضوع از آن جهت اهمیت دارد که اگر ماتریس کوواریانس به صورت یک ماتریس قطری باشد (شرط استقلال دو به دو بین متغیرها وجود داشته باشد) معکوسپذیری آن بسیار ساده خواهد بود. در نتیجه اگر متغیرها دارای همبستگی ضعیف یا قابل اغماض باشند، بهتر است آنها را در ماتریس کوواریانس برابر با صفر در نظر گرفت تا محاسبات به سادگی بیشتری همراه باشند.
$$\large x_i \perp x_j \Leftrightarrow \mathbf{\Sigma}_{ij} = 0 $$
بنابراین، اگر میخواستیم ماتریس کوواریانس به صورت یک ماتریس خلوت ظاهر شود، باید استقلال حاشیهای را بین پارامترها فرض کنیم، که این فرض یک فرض قوی و به طور کلی غیر منطقی محسوب میشود. با این حال، استقلال شرطی (از طریق خاصیت مارکوف) اغلب یک فرض بسیار منطقی است. قدرت رویکرد GMRF از آنجا ناشی میشود که خصوصیات استقلال شرطی در ماتریس دقت (یا همان کوواریانس) را لحاظ میگردد. به این ترتیب از این خاصیت برای بهبود محاسبات مربوط به این ماتریسها بهره برده و میتوان رابطه زیر را به کار برد.
$$ \large x_i \perp x_j | \mathbf{x}_{-ij} \Leftrightarrow \mathbf{Q}_{ij} = 0 $$
بنابراین فرض وجود خاصیت مارکوف در GMRF منجر به یک ماتریس دقت خلوت میشود. این خاصیت برای چنین ماتریسی به «تجزیه چولسکی» (Cholesky Factorization) نیز منتقل میشود و رابطه پایین را خواهیم داشت.
$$\large Q = LL^T $$
تجزیه بالا به سرعت محاسباتی کمک شایانی میکند، زیرا اغلب ماتریس $$Q$$ یک ماتریس با ابعاد بزرگ است و محاسبات براساس آن کار مشکلی خواهد بود. ولی تجزیه چولسکی کارها را سادهتر کرده و محاسبات را سرعت میبخشد.
تقریب لاپلاس
«بسط سری تیلور» (Taylor Series Expansion) را به یاد بیاورید، در چنین بسطی این خاصیت وجود دارد که میتوان هر تابع با شرایط مطلوب را حول یک نقطه مثل $$a$$ به جمع چندین عبارت (گاهی بینهایت عبارت) بسط و گسترش داد. استفاده از تعداد محدودی از این عبارتها میتواند به عنوان یک تقریب برای آن تابع در نظر گرفته شود.
$$ \large \begin{equation*} f(x) = f(a) + \frac{f'(a)}{1!}(x - a) + \frac{f”(a)}{2!}(x - a)^2 + \frac{f”'(a)}{3!}(x - a)^3 + \ldots \end{equation*}$$
همانطور که در رابطه بالا دیده میشود، بسط یا سری تیلور برای تابع $$f(x)$$ حول نقطه $$a$$، برای بی نهایت عبارت که با یکدیگر جمع شدهاند، نوشته شده است. البته غالباً از سه عبارت اول یعنی تا مشتق دوم برای تعیین تقریب مناسب استفاده میکنند و جملههای بعدی را نادیده میگیرند.
فرض کنید تابع مورد نظر به صورت یک سهمی یا فرمی از تابع درجه دو به شکل $$ y = x^2$$ باشد. در این صورت بسط تیلور حول نقطه $$a=2$$ به شکل زیر نوشته خواهد شد.
$$ \large \begin{align*} f(x) = x^2 \hspace{7mm} f'(x) = 2 x, \hspace{7mm} f”(x) = 2, \hspace{7mm} f”'(x) = 0 \end{align*} $$
در نتیجه خواهیم داشت:
$$ \large \begin{align*} f(x) = x^2 = 2^2 + 2(2)(x - 2) + \frac{2}{2}(x - 2)^2 \end{align*} $$
تقریبا تیلور و مقدار واقعی تابع $$f(x)=x^2$$ در نموداری که در تصویر ۱ دیده میشود، قابل مشاهده است.

برای تخمین توزیع هر یک از پارامترهای مدل که دارای «توزیع آماری نرمال» (Normal Probability Density Function) باشد، از تقریب لاپلاس استفاده میشود. از سه عبارت گفته شده برای بسط تیلور تابع درجه دوم حول نقطه «نما» (mode) که با نماد $$\widehat{x}$$ نشان داده میشود، استفاده میکنیم. البته توجه داشته باشید که در اینجا از لگاریتم تابع توزیع (یا به نوعی تابع درستنمایی - Likelihood) استفاده خواهیم کرد. لگاریتم گیری شکل تابع را برای گرفتن مشتق و محاسبات بعدی سادهتر میکند.
$$ \large \begin{align}\log g(x) \approx \log g(\hat{x}) + \frac{\partial \log g(\hat{x})} {\partial x} (x- \hat{x}) + \frac{\partial^2 \log g(\hat{x})} {2 \partial x^2} (x-\hat{x})^2\end{align} $$
مشتق اول در نقطه نما برابر با صفر است. در نتیجه عبارت بالا سادهتر خواهد شد. اگر برای واریانس توزیع نرمال (پارامتر توزیع) نیز یک برآوردگر به شکل $$\hat{\sigma}^2 = -1 / \frac{\partial^2 \log g(\hat{x})} {2 \partial x^2}$$، آنگاه میتوان عبارت بالا با به صورت تقریبی و به شکل زیر بنویسیم.
$$ \large \begin{align}\log g(x) \approx \log g(\hat{x}) – \frac{1}{2 \sigma^2} (x - \hat{x})^2 \end{align} $$
این روش میتواند یک تقریب برای توزیع نرمال به ما ارائه دهد. هر دو طرف رابطه بالا را به صورت نمایی نوشته و از هر دو طرف رابطه، انتگرال میگیریم.
$$ \large \begin{align}\int g(x) dx = \int exp[\log g(x) dx] \approx \text{constant} \int exp[ – \frac{(x - \hat{x})^2}{2 \hat{\sigma^2}} ] dx \end{align}$$
البته مقادیر ثابت را انتگرال خارج کردهایم تا کار سادهتر شود.
به این ترتیب با استفاده از تقریب لاپلاس، توزیع $$f(x)$$ تقریبا توزیع نرمال با میانگین $$\widehat{x}$$ خواهد بود. مقدار $$\widehat{x}$$ نیز با صفر قرار دادن مشتق اول و رابطههای زیر بدست خواهد آمد.
$$ \large f'(x) = 0 $$
$$ \large \hat{\sigma}^2 = - 1/f”(x) $$
البته رابطه مربوط به واریانس را در نقطه نما محاسبه خواهیم کرد. برای مثال از یک «توزیع کای ۲» (Chi-Square Distribution) استفاده میکنیم تا روند انجام محاسبات را بهتر درک کنیم.
نکته: از آنجایی که در توزیع کای ۲، مشتقگیری به سادگی صورت خواهد گرفت، از این توزیع استفاده کردهایم. همچنین توجه داشته باشید که عبارت مخرج در این توزیع به مقدار متغیر وابسته نیست. همین موضوع کار را سادهتر میکند.
$$ \large \begin{align} f(x ; \,k) & = \frac{x^{(k/2-1)} e^{- x / 2}}{2^{ k / 2} \Gamma\left(\frac{k}{2} \right)}, x \geq 0 \end{align} $$
حال عمل لگاریتم گیری را روی تابع توزیع احتمال انجام میدهیم.
$$ \large \begin{align} \ \log f(x) & = (k / 2 – 1) \log x – x / 2 \end{align}$$
مشتقگیری در مرحله بعدی صورت میگیرد و مقدار بیشینه برای آن محاسبه میشود. به یاد دارید که چنین شیوهای نیز برای تابع درستنمایی یا لگاریتم آن نیز صورت میگرفت. ولی در روش درستنمایی، مشتق بر حسب پارامتر بود و بیشینهسازی براساس آن صورت میگرفت ولی در اینجا، هدف فقط تقریب یک تابع به کمک بسط تیلور است. از آنجایی که نما (مقدار بیشینه تابع چگالی) برآورد را نشان میدهد، مشتق تابع تقریبی را محاسبه کرده تا نقطهای که آن را بیشینه میکند، بدست آمده و به عنوان مقدار برآورد (پارامتر میانگین توزیع نرمال -$$\mu$$) به کار رود.
$$ \large \begin{align} \ \log f'(x) & = (k/2 - 1) / x – 1/2 = 0 \end{align} $$
به این ترتیب طبق محاسبه انجام شده خواهیم داشت:
$$ \large \begin{align} \ \log f”(x) & = - ( k / 2 – 1 ) / x^2 \end{align} $$
در نتیجه میتوان توزیع کای ۲ را براساس توزیع نرمال با پارامترهای بدست آمده در رابطه زیر، تقریب زد.
$$ \large \begin{align} \ \therefore \chi^2_k & \overset{LA} {\sim} N(\hat{x} = k - 2, \hat{\sigma}^2 = 2(k - 2)) \end{align} $$
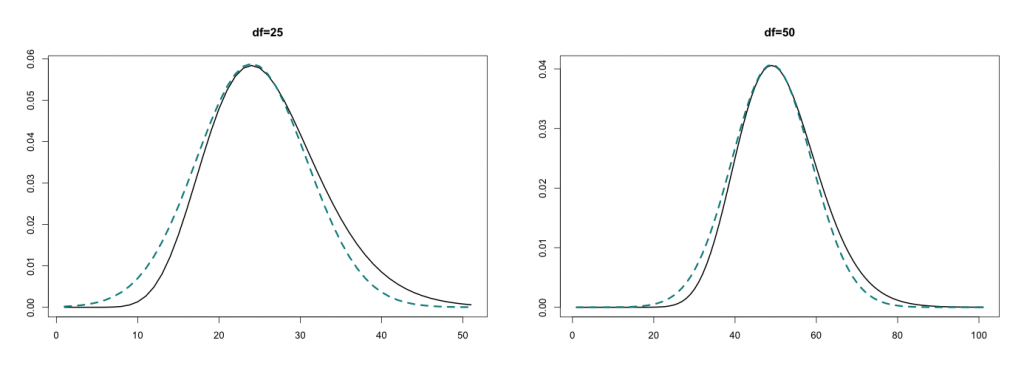
نمودارهایی که در تصاویر ۲ مشاهده میکنید، تقریب توزیع کای ۲، با رنگ مشکی و تقریب آن با توزیع نرمال (خط چین آبی) است.
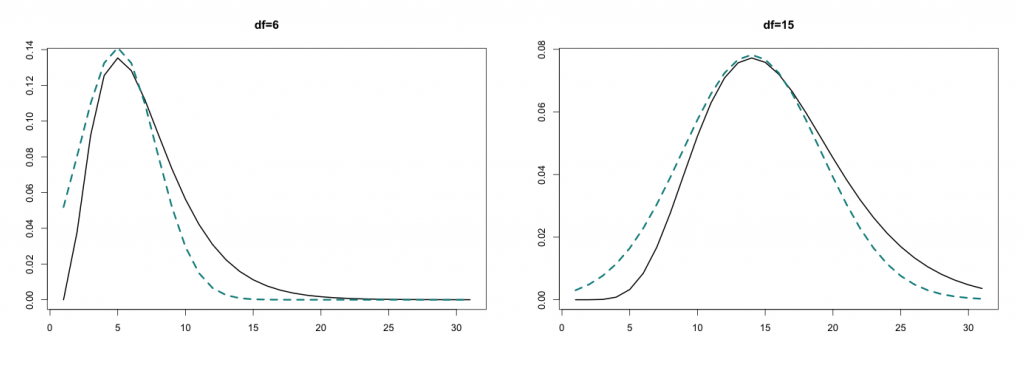
مشخص است که هنگام افزایش مقدار درجه آزادی، شکل توزیع نرمال و کای ۲ به یکدیگر نزدیکتر میشود.
همانطور که دیدید، این یک مثال بسیار ساده در حالت تک متغیره بود. ولی اگر مسئله به صورت یک مدل چند متغیره درآید، پای جبر خطی و محاسبات ماتریسی به میان آمده و پیچیدگی افزایش مییابد.
ادغام و ترکیب تقریب لاپلاس به شکل تو در تو
در ابتدای امر، به یک مثال چند متغیره بسیار ساده خواهیم پرداخت. اما هدف فقط این است که شما را متقاعد کنیم که وقتی وضعیت توزیع تقریباً نرمال است، تقریب لاپلاس تو در تو به خوبی کار میکند. به رابطه زیر توجه کنید.
$$ \large \begin{equation} p(x_j | \mathbf{y}) = \int p(x_j, \mathbf{\theta} | \mathbf{y}) d\mathbf{\theta} = \int p(x_j | \mathbf{\theta},\mathbf{y}) p(\mathbf{\theta} | \mathbf{y}) d\mathbf{\theta} \end{equation} $$
و بنابراین اطلاعاتی که برای تخمین آنها نیاز داریم عبارتند از: $$p(\mathbf{\theta}|\mathbf{y})$$ و $$p(x_j | \mathbf{\theta}, \mathbf{y})$$. اولین عبارت میتواند برای برآورد تمام توزیعهای حاشیهای مورد نظر و همچنین برای برآورد حاشیه در قسمت پنهان مورد نیاز باشد.
در مباحث مربوط به احتمال و بخصوص «احتمال شرطی» (Conditional Probability) به یاد دارید که:
$$ \large \begin{equation} p(\theta_k | \mathbf{y}) = \int p(\mathbf{\theta} | \mathbf{y}) d \mathbf{\theta}_{ - k} \end{equation} $$
$$ \large \begin{align} p(b) & = \frac{p(a,b)} {p(a|b)} \end{align} $$
$$ \large \begin{align} p(b|c) &= \frac{p(a,b|c)} {p(a|b,c)} \end{align} $$
از همین قواعد برای بازنویسی توزیع حاشیهای استفاده میکنیم. بنابراین به نتیجه زیر خواهیم رسید.
$$ \large \begin{align} p(\mathbf{\theta} | \mathbf{y}) & = \frac{p(\mathbf{x}, \mathbf{\theta} \mathbf{|} \mathbf{y})} {p(\mathbf{x} \mathbf{|} \mathbf{\theta}, \mathbf{y}) } \nonumber \end{align} $$
با بسط تیلور صورت عبارت بالا براساس تقریب لاپلاس برای مخرج به فرمولی به شکل زیر برای توزیع پسین خواهیم رسید.
$$ \large \begin{align} p(\mathbf{\theta} | \mathbf{y}) & \approx \frac{p(\mathbf{y | x, \theta}) p(\mathbf{x | \theta}) p(\mathbf{\theta})} {\tilde{p} (\mathbf{x | \theta,y})} \bigg|_{x = {x^*}(\theta)} = \tilde{p}(\mathbf{\theta|y}) \end{align} $$
در رابطه بالا، $$x^*(\theta)$$ میانه $$x$$ به شرط معلوم بودن پارامتر $$\theta$$ است. بدست آوردن $$p(x_j | \mathbf{\theta}, \mathbf{y})$$ نیز بر همین منطق استوار است که البته پیچیدهتر خواهد بود زیرا ابعاد $$x$$ بسیار بزرگتر است.
سادهترین گزینه استفاده از تقریب نرمال برای $$p(x_j | \mathbf{\theta}, \mathbf{y})$$ به طور مستقیم، است. این کار را قبلاً برای تقریب مخرج فرمول نیز انجام دادیم. مشخص است که این روش بسیار سریع عمل میکند، اما فرض خیلی قوی (مانند نرمال بودن) برای استفاده از آن لازم است. اغلب توزیعهای شرطی به صورت چوله یا دم سنگین در میآیند و این مسئله کار را مشکل میکند.
به عنوان یک روش جایگزین، میتوانیم $$x$$ را به صورت $$\mathbf{x} = [x_j, \mathbf{x}{- j}]$$، «افراز» (Partition) کنیم و از تقریب لاپلاس برای هر عنصر در قسمت پنهان $$x$$ کمک بگیریم.
$$ \large \begin{align} p(x_j | \mathbf{\theta,y}) \propto \dfrac{p(\mathbf{x,\theta |y})}{p(\mathbf{x}{-j} | x_j, \mathbf{\theta, y})} \propto \dfrac{p(\mathbf{\theta})p(\mathbf{x|\theta})p(\mathbf{y|x})}{p(\mathbf{x}_{- j} | x_j, \mathbf{\theta, y})} \end{align}$$
این روش کارایی مناسبی دارد، زیرا احتمال یا توزیع شرطی $$p(\mathbf{x_{-j}} | x_j, \mathbf{\theta, y})$$ اغلب نزدیک به توزیع نرمال است، اما از نظر محاسباتی بار بیشتری دارد.
گزینه سوم (پیش فرض در نرم افزار INLA) بهرهگیری از تقریب ساده لاپلاس است که به نوعی سازش بین دو روش قبلی است که از نظر محاسباتی بسیار کارآمد است. این روش، برای تخمین، از بسط یا سری تیلور تا مرتبه سوم هر دو عبارت صورت و مخرج $$ p(x_j|\mathbf{\theta,y})$$ استفاده میکند. الگوریتم INLA از روشهای مشابه نیوتن برای کشف و شناسایی توزیع پسین توام برای اَبَرپارامترهای $$\tilde{p}(\mathbf{\theta|y}) $$ استفاده میکند تا برای انتگرال عددی زیر، نقاط مناسب را بدست آورد.
$$ \large \begin{align*} \tilde{p}(x_j|\mathbf{y}) \approx \sum_{h=1}^H \tilde{p}(x_j | \theta^*_h,\mathbf{y}) \tilde{p}(\theta^*_h|\mathbf{y}) \Delta_h \end{align*} $$
و اکنون میتوانیم خلاصه آنچه را INLA انجام میدهد، معرفی کنیم:
- یکپارچه سازی: با استفاده از انتگرالگیری عددی، نتایج جمعبندی میشوند.
- تو در تو: چون به $$p(\mathbf{\theta | y)}$$ احتیاج داریم تا $$p(x_j | \mathbf{y}) $$ را بدست آوریم.
- تقریب لاپلاس: روشی که برای بدست آوردن پارامترهای تقریب نرمال به کار میرود، به تقریب لاپلاس مشهور است.
در ادامه به کمک کدهای زبان برنامهنویسی R، قابلیتهای الگوریتم INLA را روی دادههای شبیهسازی شده، نمایش خواهیم داد.
به کارگیری R-INLA برای پیادهسازی INLA
کتابخانه R-INLA در زبان برنامهنویسی R، به یک کتابخانه C مستقل (GMRF) متکی است و بنابراین در CRAN وجود ندارد، اما میتوانید تمام اطلاعات را با کلیک روی (+) دریافت کنید. در این بخش میخواهیم به کمک دو مثال ساده از MCMC با استفاده از RJAGS و همچنین INLA را با R-INLA را اجرا کرده و نتایج را با هم مقایسه کنیم.
یک مدل رگرسیون خطی ساده
یک مدر رگرسیون ساده را به شکل زیر در نظر بگیرید. برآورد پارامترهای این مدل در کدهایی ایجاد شده، صورت گرفته است. هر دو الگوریتم JAGS و INLA در نرمافزار R پیادهسازی شده و نتایج توسط نمودارهایی، مقایسه خواهند شد. این مدل رگرسیونی به صورت زیر نوشته شده است. واضح است که پارامترهای این مدل، عرض از مبدا ($$\alpha$$) و شبب خط ($$\beta$$) است.
$$ \large E(y_i|x_i) = \alpha + \beta x_i $$
ابتدا دادههایی برای مشخص کردن و شبیهسازی متغیر وابسته و مستقل تولید شده، سپس توابع مربوط به الگوریتمها، برای این مجموعه داده، فراخوانی شدهاند.
شبیهسازی دادهها
N = 100 #500, 5000, 25000, 100000 x = rnorm(N, mean=6,sd=2) y = rnorm(N, mean=x,sd=1) data = list(x=x,y=y,N=N)
کد مربوط به JAGS
model = function() {
for(i in 1:N) {
y[i] ~ dnorm(mu[i],tau)
mu[i] <- alpha + beta*x[i]
}
alpha ~ dnorm(0,0.001)
beta ~ dnorm(0,0.001)
tau ~ dgamma(0.01,0.01)
}
params = c("alpha","beta","tau","mu")
jags(data=data,param=params,n.chains=3,n.iter=50000, n.burnin=5000, model.file=model)
کد مربوط به INLA
inla(y~x, family = c("gaussian"), data = data, control.predictor=list(link=1))
در نمودار پایینی، مقایسهای بین برآوردalpha و beta، توسط الگوریتم riags و r-inla صورت گرفته است. به نظر میرسد که هر دو روش با هم مطابقت دارند. همانطور که در کد بالا شاهد هستیم، alpha و beta، ضرایب یک مدل رگرسیون خطی ساده هستند.
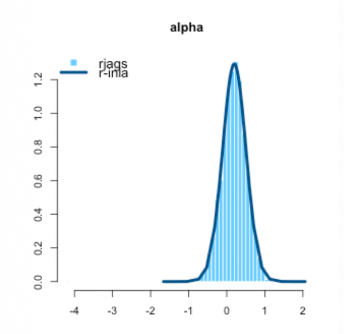
در نمودار بعدی نیز، مقایسهای بین برآورد توسط کدهای مربوط به الگوریتم riags و r-inla به زبان R، روی پارامتر $$\beta$$ انجام شده است. مطابقت هر دو مقدار در این حالت نیز وجود دارد.
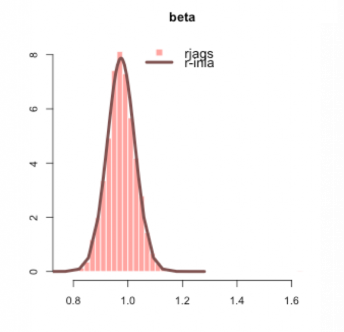
INLA یا تقریب لاپلاس، به جای توزیع تجربی شبیه سازی شده که در الگوریتم MCMC به کار میرود، توزیع پسین ایجاد کرده و از آن بهره میبرد. در شکلهای بالایی میتوانید میزان یا مقدار برآورد شده برای پارامترهای توزیع را با دو الگوریتم JAGS (هیستوگرام) و INLA (منحنی چگالی) مشاهده کنید.
در نمودار پایینی، مقدار ماتریس دقت (عکس ماتریس واریانس) که توسط الگوریتمها برآورد شده، مقایسه شده است. البته توجه داشته باشید که چون مدل تک متغیره است، به جای ماتریس فقط از واریانس یا کوواریانس در نمودار استفاده شده است. باز هم در هر دو حالت استفاده از الگوریتمها، دقت نیز یکسان حاصل شده است.
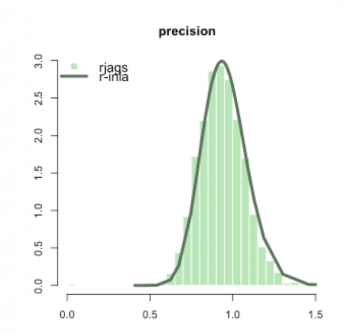
در اینجا براساس استقلال و شرطهای گفته شده، محاسبات تقریب لاپلاس ساده بودند. اما گاهی اوقات ممکن است این کار با دشواری همراه باشد. تشخیص موارد پیش فرض INLA و تعیین آنها میتوانند به یک چالش بزرگ برای حجم کوچکی از دادهها تبدیل شود. اگر محاسبات مربوط به MCMC و INLA را مقایسه کنیم، باید نتایج به یکدیگر نزدیک باشد. گاهی اوقات INLA احتیاج به یک توزیع پیشین مناسب دارد که ممکن است به صورت تابعی به فرم logit تعریف شود.
حتی برای این مثال ساده، با توجه به تغییر و افزایش اندازه نمونه صرفهجویی در زمان هنگام اجرای الگوریتم R-INLA در مقابل JAGS قابل توجه است. برای آگاهی بیشتر در این زمینه به ادامه متن توجه کنید.
تقریب لاپلاس برای مدل خطی عمومی پواسن با اثر تصادفی مستقل
در رابطههایی که در زیر دیده میشود، یک مدل پواسن (Poisson GLM) معرفی شده که پارامتر آن توسط روش INLA یا تقریب لاپلاس برآورد خواهد شد. توجه داشته باشید که برای برآورد این پارامتر از لگاریتمی استفاده شده که یک فرم خطی را نمایش میدهد. همچنین متغیرها به صورت اثر تصادفی «مستقل و هم توزیع» (iid random effect) در نظر گرفته شدهاند.
$$ \large E(y_i|x_i) = poisson(\mu_i) $$
$$ \large log(\mu_i) = \alpha + \beta x_i + \nu_i$$
$$ \large \nu_i \sim N(0,\tau_\nu) $$
مشخص است که برای توزیع پیشین نیز از توزیع نرمال با میانگین صفر استفاده شده.
کد مربوط به شبیهسازی دادهها
به منظور ارزیابی الگوریتمهای تقریب لاپلاس، یک سری داده به تعداد ۱۰۰، ۵۰۰، ۵۰۰۰، ۲۵۰۰۰ و صدهزار از توزیع نرمال تولید شده است. مدل مورد نظر در اینجا هم مدل GLM پواسن است. پارامترهای مدل هم با توزیعهای پیشین نرمال در نظر گرفته شدهاند. برای مثال $$\nu$$ در این اینجا از توزیع نرمال با میانگین صفر و انحراف معیار ۰٫۰۱ و از طرفی، «تغیر وابسته یا $$y$$ نیز از توزیع پواسن پیروی میکند، پس مدل به صورت یک مدل شمارشی یا مدل عمومی خطی خواهد بود.
N = 100 # 500, 5000, 25000, 100000 x = rnorm(N, mean=5,sd=1) nu = rnorm(N,0,0.1) mu = exp(1 + 0.5*x + nu) y = rpois(N,mu)
کد پیادهسازی JAGS در R
کدی که در ادامه مشاهده میکنید، نحوه پیادهسازی الگوریتم JAGS را در نرمافزار R به صورت یک تابع نشان میدهد. در خط آخر کد نیز با توجه به یک مثال، این تابع به کار گرفته شده و محاسبات انجام میشود.
model = function() {
for(i in 1:N) {
y[i] ~ dpois(mu[i])
log(mu[i]) <- alpha + beta*x[i] + nu[i]
nu[i] ~ dnorm(0,tau.nu)
}
alpha ~ dnorm(0,0.001)
beta ~ dnorm(0,0.001)
tau.nu ~ dgamma(0.01,0.01)
}
params = c("alpha","beta","tau.nu","mu")
jags(data=data,param=params,n.chains=3,n.iter=50000, n.burnin=5000, model.file=model)
مشخص است که مقدار alpha, beta و tau.nu، متناظر با مقادیر $$\alpha, \beta$$ و $$\tau_{nu}$$ هستند. البته در انتها نیز برای دادههای شبیهسازی شده این مدل اجرا خواهد شد. توجه داشته باشید که در اینجا تعیین پارامترهای توزیع پیشین باید توسط کاربر صورت گیرد.
کد INLA در R
nu = 1:N
inla(y ~ x + f(nu,model="iid"), family = c("poisson"),
data = data, control.predictor=list(link=1))
همانطور که میبینید کد یا شکل دستوری به کار رفته برای دستور INLA برای تقریب لاپلاس تو در تو یکپارچه در زبان برنامهنویسی R، بسیار شبیه به معرفی یک مدل رگرسیونی است. همین قابلیت، کاربران را به سادگی جذب کرده و زمان مربوط به فراگیری قالب دستوری را کاهش میدهد. در ادامه مقایسهای در مورد کارایی دو کد گفته شده خواهیم داشت.
مقایسه زمان و سرعت اجرای و همگرایی در الگوریتمهای تقریب لاپلاس
جدولی که در ادامه مشاهده میکنید، زمان همگرایی دو الگوریتم rjags و r-inla را با توجه به تعداد نمونههای متفاوت، مقایسه کرده است. زمانها به ثانیه نوشته شدهاند.
| n | rjags | r-inla |
| 100 | 30.394 |
0.383 |
| 500 | 142.532 | 1.243 |
| 5000 | 1714.468 | 5.768 |
| 25000 | 8610.32 | 30.077 |
| 100000 | عدم همگرایی پس از ۶ ساعت | 166.819 |
به وضوح قدرت روش INLA در این جدول دیده میشود. تنها چیزی که در مورد کد MCMC میتوان به عنوان مزیت معرفی کرد، علاوه بر تئوری شهودیتر آن، قالب دستوری BUGS / JAGS در مقابل INLA است. هرچند INLA زیبا به نظر میرسد، (زیرا بسیار شبیه به دستور یا تابع glm در R است) اما گاهی اوقات انتخاب توزیع پیشین به مسئله بزرگی تبدیل میشود که به سادگی از آن نمیتوان عبور کرد. به نظر میرسد کد BUGS ساختار سلسله مراتبی مدلها را به شکلی موثرتری برجسته میکند که این امر بخصوص برای آموزش و یادگیری مناسب است.
خلاصه و جمعبندی
در این نوشتار با موضوع تقریب لاپلاس به کمک روش ترکیبی زنجیره مارکوف آشنا شدیم. همانطور که دیدید، با ترکیب این دو شیوه، عملکرد بهتری برای محاسبه تقریبی و برآورد پارامترهای مدل یا توزیع بوجود میآید که به آن تقریب لاپلاس تو در تو یکپارچه (Integrated Nested Laplace Approximation) گفته میشود. در این بین با خصوصیات مربوط به این شیوه محاسباتی نیز آشنا شدیم و نحوه پیادسازی آن را در هم در محیط برنامهنویسی R فرا گرفتیم. در انتها از لحاظ زمانی و سرعت همگرایی، الگوریتم INLA را با شیوه مشابه با الگوریتم MCMC مقایسه کرده و نتیجه گرفتیم که روش INLA سریعتر عمل میکند.










