فرادرس
متد مونت کارلو – به زبان ساده
در این آموزش قصد داریم تا در خصوص متد مونت کارلو به بحث بپردازیم و به کمک مثال پرتاب تاس، این موضوع را شرح دهیم. همچنین در انتها، دقت نتایج و تاریخچه مونت‌کارلو مورد بررسی قرار خواهد گرفت.
متد مونت کارلو چیست؟
به صورت کلی، متد مونت کارلو (یا شبیه سازی مونت کارلو) به هر تکنیکی اتلاق می‌شود که از طریق نمونه‌سازی آماری، پاسخ‌های تقریبی برای مسائل کمّی فراهم می‌کند. شبیه‌سازی مونت کارلو بیشتر برای توصیف روشی جهت انتشار عدم قطعیت‌های موجود در ورودی مدل به عدم قطعیت‌ها در خروجی مدل، به کار می‌رود. بنابراین مونت‌کارلو، نوعی شبیه‌سازی است که به طور صریح و کمی، عدم قطعیت را نمایش می‌دهد. شبیه‌سازی مونت کارلو متکی به فرآیند نمایش صریح عدم قطعیت با تعیین ورودی‌ها به عنوان توزیع‌های احتمال است. اگر ورودی‌های توصیف‌کننده یک سیستم، غیرقطعی باشند، آنگاه پیش‌بینی عملکرد پیش رو به طور قطع غیرقطعی است. این بدان معنی است که نتیجه هر گونه تحلیل مبتنی بر ورودی‌های نمایش داده شده با توزیع‌های احتمال، خود یک توزیع احتمال است.
احتمال مشروط در متد مونت کارلو
از آنجایی‌که نتیجه شبیه‌سازی یک سیستم غیرقطعی، یک گزارش مشروط است - به طور مثال: اگر سد بسازیم، ماهی‌های سالمون منقرض می‌شوند - نتیجه یک شبیه‌سازی احتمالی (مونت کارلو) یک احتمال مشروط خواهد بود یعنی به طور مثال: اگر سد بسازیم، ۲۰ درصد شانس وجود دارد که ماهی‌های سالمون منقرض شوند. بیان کمی شانس منقرض شدن، اغلب برای آن دسته از تصمی‌گیرندگانی مفید است که از نتایج شبیه‌سازی استفاده می‌کنند.
به منظور محاسبه توزیع احتمال کارایی پیش‌بینی شده، لازم است تا عدم قطعیت‌های ورودی به عدم قطعیت‌های خروجی منتقل شود. متدهای گوناگی برای انتقال عدم قطعیت وجود دارند. شبیه‌سازی مونت کارلو احتمالا رایج‌ترین تکنیک برای انتشار عدم قطعیت موجود در جنبه‌های مختلف یک سیستم به کارایی پیش‌بینی شده است.
تحقق سیستم در متد مونت کارلو
در شبیه‌سازی مونت کارلو، کل سیستم به تعداد دفعات زیادی در حدود 1000 بار اجرا می‌شود. به هر بار شبیه‌سازی، تحقق (Realization) سیستم گفته می‌شود. برای هر تحقق، تمام پارامترهای غیرقطعی نمونه‌برداری خواهند شد که یعنی یک مقدار تصادفی از توزیع اختصاصی مربوط به هر پارامتر، انتخاب می‌شود. سپس، این سیستم با پارامترهای ورودی معین، در طول زمان، شبیه‌سازی خواهد شد. این شبیه‌سازی به گونه‌ای انجام می‌شود که در نهایت بتوانیم کارایی سیستم را محاسبه کنیم. این امر منتج به ایجاد تعداد زیادی نتیجه مستقل و جداگانه می‌شود، که هر کدام بیانگر یک «آینده» احتمالی برای سیستم هستند. به عبارت دیگر، یعنی یک مسیر احتمالی خواهیم داشت که سیستم، با گذشت زمان آن‌را دنبال خواهد کرد. نتایج تحقق‌های مستقل سیستم به شکل توزیع‌های احتمالی خروجی‌های ممکن خواهد بود. در نتیجه، خروجی‌ها به صورت مقادیر تک نیستند، بلکه توزیع احتمال هستند.
پرتاب تاس، مثالی ساده از شبیه سازی مونت‌کارلو
یک مثال ساده از شبیه‌سازی مونت کارلو را می‌توان در نظر گرفتن احتمال رخداد حاصل جمع مشخص از پرتاب دو تاس در نظر گرفت. روی هر وجه از این تاس‌ها، اعداد ۱ تا ۶ نوشته شده است. (هر کدام از تاس ها شامل اعداد 1 تا 6 هستند). در این مورد خاص، 36 ترکیب مختلف برای حاصل جمع تاس‌های پرتاب شده وجود دارد:
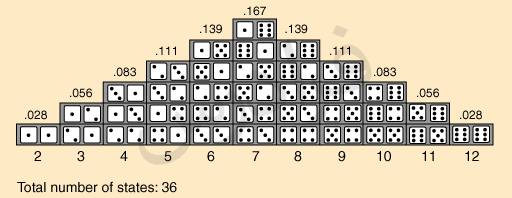
می‌توانید به صورت دستی احتمال یک خروجی خاص را محاسبه کنید. برای مثال، شش حالت مختلف وجود دارد که مجموع تاس‌ها هفت شود. بنابراین، احتمال هفت شدن مجموع تاس‌ها برابر است با تقسیم 6 بر 36 که حاصل این تقسیم، عدد 0.167 خواهد بود.
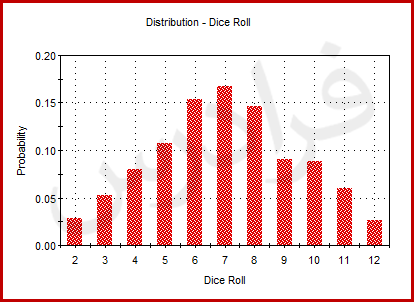
به جای محاسبه احتمال بدین طریق، می‌توانیم یک تاس را صد بار پرتاب و محاسبه کنیم که هر خروجی چند بار رخ می‌دهد. اگر مجموع تاس‌ها از 100 پرتاب، هجده بار برابر هفت شود، می‌توانیم نتیجه بگیریم که احتمال هفت شدن خروجی تقریبا برابر با 0.18 یا 18 درصد است. به طور واضح دیده می‌شود که هر چه بیشتر تاس‌ها را پرتاب کنیم، خروجی دقیق‌تر خواهد بود. راه بهتر از پرتاب تاس‌ها این است که از یک کامپیوتر برای شبیه‌سازی تاس‌ها استفاده کنیم و آنها را 10000 بار یا بیشتر پرتاب کنیم. از آنجا که در هر پرتاب، احتمال هر یک از اعداد، برابر با $$1/6$$ است، کار ساده‌ای در پیش داریم. در تصویر زیر، خروجی 10000 بار تحقق سیستم به کمک نرم‌افزار «GoldSim» را مشاهده می‌کنید.
دقت نتایج شبیه سازی مونت‌کارلو
دقت شبیه‌سازی مونت کارلو تابعی از تعداد تحقق سیستم است (تعداد اجراها). این بدان معنی‌ست که بازه اطمینان نتایج را می‌توان از روی تعداد تحقق‌ها نوشت. دو مثال زیر بازه اطمینان 5% و 95% را برای مقدار هر خروجی نشان می‌دهند (یعنی 90% شانس وجود دارد که این بازه شامل مقدار واقعی باشد).
در تصویر زیر، 100 بار تحقیق سیستم را خواهیم داشت:
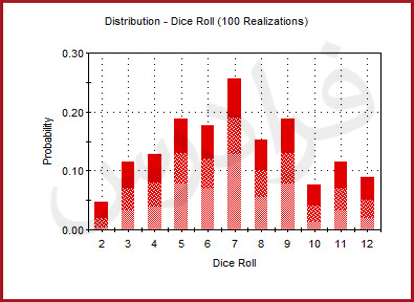
در این تصویر، همانطور که مشاهده می‌کنید، تحقق سیستم برای 1000 بار نمایش داده شده است:
تاریخچه روش مونت کارلو
نام شبیه‌سازی مونت کارلو از شهری در موناکو گرفته شده است که در آن بازی‌های شانسی با رخدادهای تکرارشونده و احتمال‌های مشخص، رواج دارد.
اگر این مطلب برای شما مفید بوده است، آموزش‌ها و مطالب زیر نیز به شما پیشنهاد می‌شوند:
هزاران لایک