برآوردگر اریب و نااریب — به زبان ساده

در نظریه آمار و احتمال (Statistical Theory)، برآوردگرها (Estimators) نقش اساسی و مهمی ایفا می‌کنند. هر برآوردگر برای پارامتر جامعه، تابعی از نمونه تصادفی است که به عنوان حدسی نزدیک به یقین برای پارامتر مجهول جامعه، در نظر گرفته می‌شود. با مشخص شدن مقادیر نمونه تصادفی می‌توان به کمک برآوردگر، مقدار پارامتر را به صورت تقریبی و البته احتمالی، مشخص کرد. در این نوشتار به یکی از خصوصیات جالب برآوردگرها به نام اُریبی و نااُریبی می‌پردازیم. در این بین برآوردگر اریب و نااریب برای بعضی از پارامترهای جامعه نیز طی مثال‌هایی معرفی خواهند شد. همچنین مفهوم میانه-نااریب به عنوان یک معیار برای نمایش خصوصیات دلخواه برآوردگرها نیز مورد بحث قرار خواهد گرفت.

برای آگاهی بیشتر از اصطلاحاتی که در این نوشتار به آن‌ها برخورد خواهید کرد، بهتر است مطالب دیگر از مجله فرادرس مانند امید ریاضی (Mathematical Expectation) — مفاهیم و کاربردها و استنباط و آزمون فرض آماری — مفاهیم و اصطلاحات را مطالعه کنید. همچنین خواندن متن متغیر تصادفی، تابع احتمال و تابع توزیع احتمال و تابع درست نمایی (Likelihood Function) و کاربردهای آن — به زبان ساده نیز خالی از لطف نیست.

برآوردگر اریب و نااریب

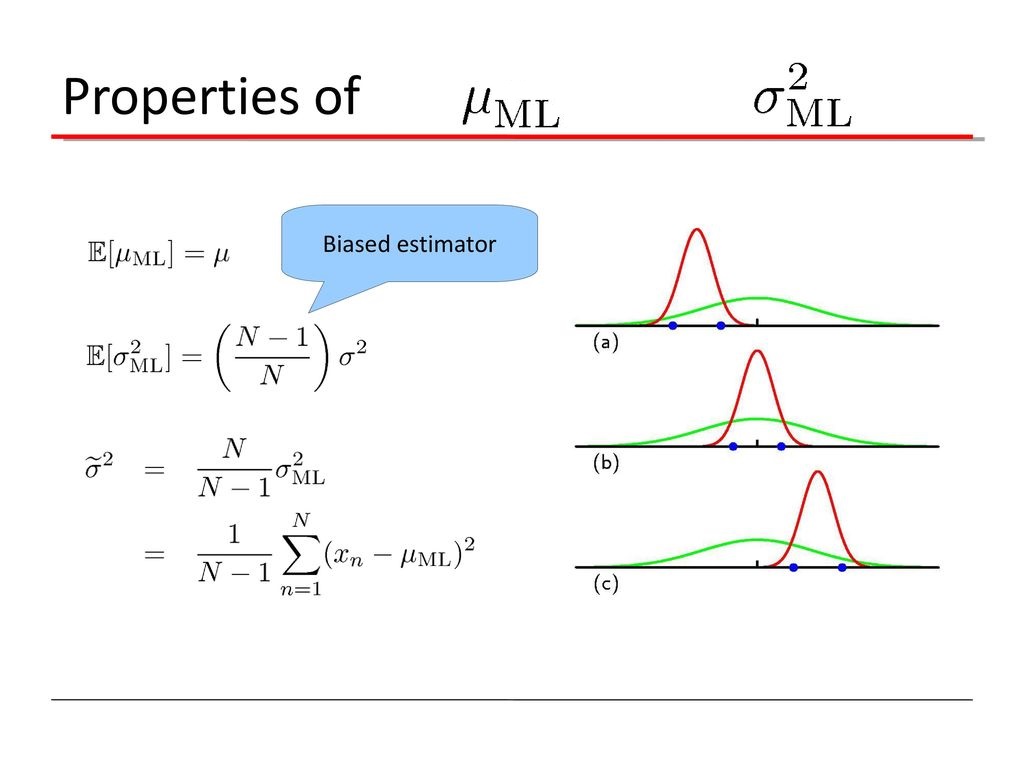
اریبی (Bias) که در فارسی گاهی آن را «تورِشی» نیز می‌نامند، ابزار و معیاری برای نشان دادن میزان نزدیکی پارامتر جامعه به برآوردگر آن پارامتر است. از آنجایی که براساس هر نمونه تصادفی، برآوردگر مربوط به پارامتر مقدار متفاوتی خواهد داشت، انتظار داریم که با تکرار نمونه‌گیری‌ها، متوسط مقدار برآوردگرهای حاصل، با پارامتر واقعی جامعه تقریبا برابر شود. در این حالت میزان اریبی برآوردگر (فاصله آن از مقدار واقعی پارامتر) باید با مقدار صفر برابر باشد. چنین برآوردگری را یک برآوردگر «نااریب» (Unbiased) می‌گویند. در حقیقت وجود چنین خاصیتی برآوردگرهای پارامتر را به دو کلاس برآوردگر اریب و نااریب تفکیک می‌کند.

فیلم آموزش آمار و کاربرد آن در مدیریت 2 در فرادرس

کلیک کنید

همانطور که گفته شد، اریبی برآوردگر را به واسط محاسبه میانگین یا متوسط مقدار آن برای نمونه‌های تصادفی مختلف، مشخص کردیم. ولی ممکن است به جای استفاده از میانگین مقادیر از میانه آن‌ها استفاده شود. در این صورت اگر میانه مقادیر برآوردگر در این نمونه‌ها با پارامتر واقعی جامعه برابر باشد، برآوردگر را «میانه-نااریب» (Median-Unbiased) می‌گویند. البته در ادامه هر دو مفهوم ذکر شده را به دقت بیشتر و به صورت رابطه‌های ریاضی و آماری معرفی خواهیم کرد.

از آنجایی که وجود خاصیت نااریبی در برآوردگرها اهمیت دارد، کلاسی از برآوردگرها نیز با این نام مشخص می‌شود. برای مثال کلاس برآوردگرهای نااریب، برای پارامترهایشان دارای اریبی صفر هستند.

ممکن است عضوی از کلاس یا خانواده برآوردگرهای نااریب نسبت به یک برآوردگر خارج از این کلاس، دارای واریانس (Variance) بیشتری یا در حقیقت دقت کمتری باشد. در نتیجه همیشه وجود خاصیت نااریبی دلیلی بر برتری برآوردگرها نیست. در نتیجه باید نااریبی را فقط به عنوان یکی از خصوصیات بهینه مربوط به برآوردگر، مورد توجه قرار داد. «حداقل بودن واریانس» (Minimum Variance)، «سازگاری» (Consistency) و «ناوردایی» (Invariant) از دیگر مشخصاتی هستند که به منظور پیدا کردن برآوردگر مناسب برای پارامتر نامعلوم جامعه مورد استفاده قرار می‌گیرند.

نکته: برآوردگری که نااریب بوده و کمترین واریانس را در همه فضای پارامتر داشته باشد، به اصطلاح UMVUE یا «برآوردگر نااریب با کمترین واریانس یکنواخت» (Uniformly Minimum Variance Unbiased Estimator) نامیده می‌شود.

هر چند برآوردگرهای نااریب در اغلب موارد برای برآورد پارامتر جامعه مورد استفاده قرار می‌گیرند ولی گاهی لازم است که برآوردگر اریب را محاسبه و پیدا کنیم. در ادامه فهرستی از این علت‌ها و مقایسه‌ای بین برآوردگر اریب و نااریب را مشاهده می‌کنید.

• پیدا کردن برآوردگر نااریب مشکل است یا اصلا برآوردگر نااریب برای پارامتر وجود ندارد.
• برای پیدا کردن برآوردگر نااریب باید جامعه آماری دارای شرایط خاصی باشد که از وجود آن‌ها مطمئن نیستیم.
• ممکن است یک برآوردگر، میانه-نااریب باشد. در نتیجه خاصیت نااریبی را به شکل دیگری در خود دارد.
• ممکن است یک برآوردگر اریب، دارای واریانس کوچکتری از برآوردگر نااریب باشد، در نتیجه دارای دقت بیشتری برای برآورد کردن پارامتر جامعه است.
• برآوردگر اریب، براساس یک تابع زیان خاص، دارای کمینه مقدار نسبت به برآوردگر نااریب (مانند برآوردگرهای کوتاه شده یا انقباضی -Shrinkage Estimator) است.
• برآوردگر نااریب مفید نبوده و یا دارای شرایط سختی برای وجود است.
• برآوردگر نااریب در فضای پارامتری قرار نمی‌گیرد. به این معنی که نتیجه حاصل از برآوردگر نااریب مقداری خارج از مقادیر مورد انتظار برای پارامتر جامعه است.

تعریف برآوردگر اریب و نااریب

فرض کنید در یک مدل آماری، مقدار حقیقی $$\theta$$ به عنوان پارامتر جامعه آماری در نظر گرفته شده باشد. در نتیجه تابع احتمال در این جامعه برحسب این پارامتر و براساس متغیر تصادفی $$X$$ خواهد بود که البته به صورت زیر نوشته می‌شود.

$$\large \text{P}_{\theta}(x) = \text{P}(x | \theta)$$

تابع $$\widehat{\theta}$$ را یک برآوردگر برای $$\theta$$ در نظر بگیرد که مقدار آن برحسب نمونه تصادفی بدست می‌آید. به این ترتیب توزیع احتمالی جامعه آماری با فرض ثابت بودن پارامتر $$\theta$$، به صورت $$\text{P}(x | \theta)$$ مشخص می‌شود.

تعریف اریبی

میزان اریبی برآوردگر $$\widehat{\theta}$$ نسبت به پارامتر $$\theta$$ به صورت زیر تعریف می‌شود.

$$\large {\displaystyle \operatorname {Bias}_{\theta }[ \, { \hat { \theta } } \, ] = \operatorname {E} _{x \mid \theta } [\, { \hat { \theta }} \, ] - \theta = \operatorname {E} _{x \mid \theta } [ \, { \hat {\theta } } - \theta \, ] }$$

رابطه ۱

توجه دارید که در اینجا منظور از $$\text{E}_{x|\theta}$$ مقدار مورد انتظار (Expected Value) یا همان امید ریاضی (Mathematical Expectation) متغیر تصادفی است. مشخص است که در اینجا متغیر تصادفی همان $$\widehat{\theta}$$ است و مقدار امید ریاضی تحت احتمال شرطی $$\text{P}(x|\theta)$$ محاسبه می‌شود.

تعریف برآوردگر نااریب

برآوردگر را نااریب (Unbiased) گویند، اگر مقدار اریبی آن طبق رابطه ۱، برای همه مقادیر پارامتر، برابر با صفر باشد.

$$\large {\operatorname {E} _{x \mid \theta } [\, { \hat { \theta }} \, ] - \theta = \operatorname {E} _{x \mid \theta } [ \, { \hat {\theta } } - \theta \, ] } = 0$$

یا به طور مشابه امید ریاضی برآوردگر پارامتر برابر با خود پارامتر باشد.

$$\large {\operatorname {E} _{x \mid \theta } [\, { \hat { \theta }} \, ] = \theta }$$

همانطور که مشاهده کردید، تابع زیان در تعریف به کار رفته برای برآوردگر اریب و نااریب، همان تفاصل دو مقدار است. قبلا اشاره کردیم که ممکن است نااریبی براساس توابع زیان دیگر تعریف شود. برای مثال، برآوردگر کمترین-واریانس میانگین-نااریب (Minimum-Variance Mean-Unbiased)، «تابع زیان مربع خطا» (Squared Error Loss Function) را کمینه می‌کند. این موضوع توسط دانشمند بزرگ آلمانی «کارل گاوس» (Carl Gauss) در قرن ۱۸ میلادی مورد توجه و بررسی قرار گرفت.

در مقابل برآوردگر کمترین-میانگین قدر مطلق میانه-نااریب (Minimum-average Absolute Deviation Median-unbiased Estimator)، تابع زیان قدر مطلق خطا (Absolute Loss Function) را کمینه می‌سازد. این موضوع توسط ریاضی‌دان بزرگ و مهندس فرانسوی، «پیر لاپلاس» (Pierre Laplace) که هم دوره با کارل گاوس بود، تحقیق شد. همچنین ممکن است توابع زیان دیگری نیز به منظور پیدا کردن برآوردگرها استوار (Robust) در کلاس‌های مختلف از برآوردگرها به کار گرفته شود.

مثال و کاربردهای برآوردگر اریب و نااریب

پیدا کردن برآوردگرهای نااریب اغلب توسط محاسبه رابطه ۱ صورت می‌گیرد و برآوردگر $$\widehat{\theta}$$ به شکلی محاسبه می‌شود که مقدار این رابطه برابر با صفر شود. در ادامه به بعضی از توزیع‌ها و پارامترهایشان اشاره می‌کنیم که دارای برآوردگر نااریب هستند. البته گاهی هم ممکن است برآوردگر اریب، دارای واریانس کوچکتری باشد که آن را هم مورد بحث قرار خواهیم داد.

فیلم آموزش رایگان اس پی اس اس SPSS – سریع و آسان در 110 دقیقه در فرادرس

کلیک کنید

برآوردگر اریب و نااریب برای حداکثر مقدار در توزیع یکنواخت گسسته

فرض کنید از توزیع یکنواخت گسسته می‌خواهیم پارامتر $$n$$ را برآورد کنیم. برای مثال فرض کنید قرار است از بین $$n$$ کارت که از ۱ تا $$n$$ شماره‌گذاری شده‌اند، یک کارت به تصادف خارج می‌کنیم و می‌خواهیم براساس همین مشاهده مقدار پارامتر $$n$$‌ را برآورد کنیم. اگر شماره کارت انتخابی را $$X$$ در نظر بگیریم، برآوردگر حداکثر درستنمایی (MLE) در این حالت برای $$n$$، همان $$X$$ است. از طرفی امید ریاضی برای $$X$$ برابر است با:

$$\large \text{E}_{n} (X) = \dfrac{ n+1 }{ 2 }$$

که مشخص است این برآوردگر، اریب است زیرا امید ریاضی آن برابر با $$n$$ نشده است. برای بدست آوردن یک برآوردگر نااریب، عملیات زیر را اجرا خواهیم کرد.

$$\large \text{ E }_{ \theta } ( X ) - \dfrac{1}{2} = \dfrac{ n } { 2 } \rightarrow 2 \left( \text{ E }_{ \theta } ( X ) - \dfrac{1}{2} \right ) = n$$

در نتیجه برآوردگر نااریب برای $$n$$ به صورت زیر، مورد محاسبه قرار می‌گیرد.

$$\large  \text{ E }_{ \theta } \left(2\;[\;X  - \dfrac{1}{2}] \right)  = n$$

پس داریم:

$$\large \widehat{n} = ( 2 X -1 )$$

پس $$2 X - 1$$ برآوردگر نااریب برای پارامتر توزیع یکنواخت گسسته یعنی $$n$$ خواهد بود.

برای مثال فرض کنید شماره کارت مشاهده شده برابر با ۱۲ باشد، در این صورت تعداد کارت‌ها براساس برآوردگر مورد نظر برابر است با:

$$\large \widehat{n} = ( 2 X -1 )  = 2 \times 12 - 1 = 24 - 1 = 23$$

برآوردگر اریب و نااریب برای احتمال توزیع پواسن

همانطور که گفته شد، ممکن است برآوردگر اریب و نااریب دارای واریانس‌های متفاوتی باشند و مثلا برآوردگر اریب، واریانس کوچکتری نسبت به برآوردگر نااریب داشته باشد. این موضوع را برای مقدار احتمال توزیع پواسن می‌توان نشان داد.

فرض کنید $$X$$ یک متغیر تصادفی با توزیع پواسن (Poisson Distribution) با پارامتر $$\lambda$$ باشد. قرار است مقدار مربع احتمال $$X = 0$$ را براساس یک مشاهده، محاسبه کنیم. در این صورت داریم:

$$\large X \sim \text{ Poisson } (\lambda) ,\;\; [P( X = 0 )]^2 = e^{- 2 \lambda}$$

رابطه ۲

برای مثال فرض کنید که در یک مرکز تلفن که تعداد تماس‌های برقرار شده در هر دقیقه از توزیع پواسن پیروی می‌کند، می‌خواهیم احتمال این را محاسبه کنیم که در یک مقطع ۲ دقیقه‌ای ($$2 \lambda$$)، هیچ تماسی برقرار نشود، به شرطی که به طور متوسط در هر دقیقه به تعداد $$\lambda$$ تماس برقرار می‌شود. واضح است که پارامتر این توزیع همان $$\lambda$$ خواهد بود.

می‌دانیم که در توزیع پواسن، پارامتر $$\lambda$$ برابر است با متوسط تعداد تماس‌های برقرار شده. براساس تعریف امید ریاضی برای یک تابع از متغیر تصادفی (که در اینجا مقدار احتمال است)، خواهیم داشت:

$$\large {\displaystyle \operatorname {E} (\delta (X) ) = \sum _{ x = 0 }^{\infty }\delta ( x ){\frac {\lambda ^{x}e^{ - \lambda }}{ x! }} = e^{ -2 \lambda }}$$

با توجه به بسط یا سری تیلور (Tailor Series) رابطه سمت راست تساوی بالا، مشخص است که باید تابع $$\delta(x)$$ به صورت زیر باشد.

$$\large \delta (x) = ( -1 )^{ x }$$

در این صورت اگر مقدار $$x=2$$ باشد، مقدار برآوردگر برابر است با ۱ که برای پارامتر توزیع پواسن مقداری معقول به نظر می‌رسد. حال فرض کنید که $$x=100$$ باشد، آنگاه باز هم مقدار برآوردگر برابر است با ۱ ولی با توجه به مقدار $$X$$ باید $$\lambda$$ بسیار کوچک و نزدیک به صفر باشد. مشخص است که مقدار برآورد از مقدار واقعی پارامتر بسیار دور است. در حقیقت $$X=100$$‌ نشان داده است که مقدار احتمال برای هیچ تماس باید بسیار نزدیک به صفر باشد در حالیکه برآورد برابر با ۱ است.

به صورت معکوس اگر تعداد تماس‌ها برابر با $$X=101$$ باشد، مقدار احتمال برابر است با ۱- که اصلا در بازه پارامتر قرار نمی‌گیرد (مقدار احتمال باید در بازه ۰ تا ۱ باشد).

همانطور که دیدید، برآوردگر نااریب دارای واریانس زیاد بوده و با تغییر کمی در مقدار مشاهدات، تغییرات زیادی دارد. در نتیجه چنین برآوردگر برای استفاده و برآورد پارامتر جامعه، مناسب نیست. حال به بررسی برآوردگر اریب برای این پارامتر می‌پردازیم.

برآوردگر حداکثر درستنمایی برای پارامتر $$e^{-2\lambda}$$ برابر است با $$e ^ {-2X}$$. واضح است که این برآوردگر همیشه مثبت است و دارای مقدار مربع خطای کمتری نسبت به برآوردگر نااریب قبلی است.

$$\large \text{E}(e^{-2X} - e^{-2\lambda})^2= e^{-4 \lambda } - 2 e^{\lambda (1/e^{2} - 3)} + e^{\lambda (1/e^{4} - 1)}$$

در حالیکه مقدار مربعات خطای (مربع فاصله برآوردگر از پارامتر) برای برآوردگر نااریب به صورت زیر محاسبه خواهد شد.

$$\large \text{E}((-1)^x - e^{-2\lambda})^2=1-e^{-4\lambda }$$

نکته: مقدار اریبی برای برآوردگر اریب در اینجا برابر است با:

$$\large \text{Bias}(e^{-2X})= e^{-2\lambda }-e^{\lambda (1/e^{2}-1)}$$

برآوردگر اریب و نااریب واریانس نمونه

در این قسمت می‌خواهیم در مورد واریانس نمونه‌ای به عنوان یک برآوردگر برای واریانس جامعه، صحبت کنیم. نشان خواهیم داد که واریانس نمونه‌ای به شکلی که در ادامه مشخص شده است، یک برآوردگر نااریب نیست. سپس براساس این برآوردگر به دنبال یک برآوردگر نااریب خواهیم گشت. واریانس نمونه‌ای در رابطه زیر مشخص شده است.

$$\large {\displaystyle {\overline {X}}\, = { \frac {1}{n} }\sum _{ i = 1 }^{n} X_{i} \qquad S^{ 2 } = { \frac {1}{n}} \sum_{ i = 1 }^{n}{ \big (}X_{i} - {\overline {X}} \,{ \big )}^{2} \qquad }$$

رابطه ۳

متاسفانه دو مشکل عمده برای این برآوردگر وجود دارد. در وحله اول، این برآوردگر نااریب نیست. البته با کمی تغییر و به کمک گرفتن از یک ضریب تصحیح می‌توان آن را نااریب کرد. این کار از طریق تقسیم مجموع مربعات خطا بر $$n-1$$ حاصل می‌شود که در ادامه خواهد آمد.

از طرف دیگر، برآوردگر $$S^2$$ میانگین مربعات خطا (MSE) را کمینه نمی‌کند. کمینه‌سازی نیز با استفاده از یک ضریب دیگر امکان‌پذیر خواهد بود. به این ترتیب یک برآوردگر اریب با MSE کمتر نسبت به $$S^2$$ بوجود خواهد آمد که از طریق نسبت مجموع مربعات اختلافات به $$n+1$$ ایجاد می‌شود.

فرض کنید $$X_1 X_2,\ldots,X_n$$ نمونه‌ای تصادفی هم‌توزیع و مستقل (iid) با میانگین $$\mu$$ و واریانس $$\sigma^2$$ باشند. اگر میانگین نمونه‌ای و واریانس نمونه‌ای طبق رابطه ۳ تعریف شده باشند، برآوردگر $$S^2$$ یک برآوردگر اریب برای $$\sigma^2$$‌ است، زیرا:

$$\large {\displaystyle {\begin{aligned}\operatorname {E} [S^{2}] & = \operatorname {E} \left[{\frac {1}{n}}\sum _{i = 1}^{n}{\big (}X_{i} - {\overline {X}}{\big )}^{2}\right] = \operatorname {E} {\bigg [}{\frac {1}{n}}\sum _{i = 1}^{n}{\bigg (}(X_{i} - \mu ) - ({\overline {X}} - \mu ){\bigg )}^{2}{\bigg ]} \\[8pt] \large & = \operatorname {E} {\bigg [}{\frac {1}{n}}\sum _{ i = 1 }^{n}{\bigg (}(X_{i}-\mu )^{2}-2({\overline {X}}-\mu )(X_{i}-\mu ) + ({\overline {X}}-\mu )^{2}{\bigg )}{\bigg ]}\\[8pt] \large & = \operatorname {E} {\bigg [}{\frac {1}{n}}\sum _{i = 1}^{n}(X_{i} - \mu )^{2}-{\frac {2}{n}}({\overline {X}}-\mu )\sum _{i = 1}^{n}(X_{i}-\mu )+{\frac {1}{n}}({\overline {X}}-\mu )^{2}\sum _{i = 1}^{n}1{\bigg ]} \\[8pt] \large & = \operatorname {E} {\bigg [}{\frac {1}{n}}\sum _{ i = 1 }^{n}(X_{i} - \mu )^{2} - {\frac {2}{n}}({\overline {X}}-\mu )\sum _{i = 1}^{n}(X_{i} - \mu )+{\frac {1}{n}}({\overline {X}}-\mu )^{2}\cdot n{\bigg ]}\\[8pt]& \large =\operatorname {E} {\bigg [}{\frac {1}{n}}\sum _{i = 1}^{n}(X_{i} - \mu )^{2}-{\frac {2}{n}}({\overline {X}}-\mu )\sum _{i = 1}^{n}(X_{i} - \mu ) + ({\overline {X}} - \mu )^{2}{\bigg ]}\\[8pt]\end{aligned}}}$$

رابطه ۴

در نظر داشته باشید که با کم کردن $$\mu$$ از دو طرف رابطه مربوط به میانگین نمونه‌ای خواهیم داشت:

$$\large { \displaystyle { \begin{aligned} { \overline {X}}-\mu ={ \frac {1}{n}}\sum _{i = 1 }^{n}X_{i}-\mu ={ \frac {1}{n}} \sum _{i = 1}^{n} X_{i} - { \frac {1}{n}} \sum _{ i= 1}^{n}\mu \ = { \frac {1}{n} } \sum _{i = 1}^{n}(X_{i} - \mu ) \\[8pt] \end{aligned} } }$$

به این ترتیب به رابطه زیر خواهیم رسید:

$$\large { \displaystyle n \cdot ( { \overline {X }} - \mu ) = \sum _{i = 1}^{n}(X_{i} - \mu )} { \displaystyle n \cdot ({ \overline {X}}-\mu ) = \sum _{i=1}^{n}(X_{i} -\mu ) }$$

اگر امید ریاضی واریانس نمونه‌ای یا $$S^2$$ را که در رابطه ۴ دیده می‌شود، بازنویسی می‌کنیم، خواهیم داشت:

$$\large {\displaystyle {\begin{aligned}\operatorname {E} [S^{2}] & = \operatorname {E} { \bigg [}{ \frac {1}{n}} \sum _{ i = 1 }^{n}(X_{i}-\mu )^{2} - {\frac {2}{n}}({\overline {X}} - \mu )\sum _{i=1}^{n}(X_{i}-\mu ) + ({\overline {X}} - \mu )^{2}{\bigg ]}\\[8pt] \large & = \operatorname {E} {\bigg [}{\frac {1}{n}}\sum _{i=1}^{n}(X_{i}-\mu )^{2} - {\frac {2}{n}} ( {\overline {X}} - \mu ) \cdot n \cdot ({\overline {X}} - \mu ) + ({\overline {X}} - \mu )^{2}{\bigg ]} \\[8pt] \large & = \operatorname {E} {\bigg [}{\frac {1}{n}}\sum _{ i = 1 }^{n}(X_{i}-\mu )^{2} - 2({\overline {X}} - \mu )^{2} + ({\overline {X}} - \mu )^{2}{\bigg ]}\\[8pt] \large & = \operatorname {E} {\bigg [}{\frac {1}{n}}\sum _{i=1}^{n}(X_{i}-\mu )^{2} - ({\overline {X}} - \mu )^{2}{\bigg ]}\\[8pt] \large & = \operatorname {E} {\bigg [}{\frac {1}{n}}\sum _{i=1}^{n}(X_{i}-\mu )^{2} {\bigg ]} - \operatorname {E} { \bigg [ }( {\overline {X}}-\mu )^{2} {\bigg ] } \\[8pt] \large & = \sigma ^{2} - \operatorname {E} \left[ ( {\overline {X}}-\mu )^{2}\right ] = \left( 1 - {\frac {1}{n}} \right) \sigma ^{2}< \sigma ^{2} \end{aligned} } }$$

رابطه ۵

به بیان دیگر، مقدار مورد انتظار (امید ریاضی) برای واریانس نمونه‌ای $$S^2$$ برابر با $$\sigma^2$$ نیست. در حالیکه میانگین نمونه‌ای ($$\overline{X}$$) یک برآوردگر نااریب برای میانگین جامعه آماری است.

نکته: می‌دانیم که واریانس میانگین نمونه‌ای برابر است با $$\frac{ \sigma^2 }{ n }$$. واضح است که سطر آخر رابطه ۵ بر این اساس نوشته شده است.

در نظر بگیرید که می‌خواهیم به کمک رابطه ۵، برآورد نااریبی برای واریانس جامعه آماری برحسب واریانس نمونه‌ای بسازیم. واضح است با توجه به رابطه ۵، اگر واریانس نمونه‌ای را در یک عامل یا فاکتور اصلاح ضرب کنیم، نااریب خواهد شد. به این ترتیب خواهیم داشت:

$$\large \text{E} ( S^2 ) = (1 - \dfrac{1}{n})\sigma^2, \; \; \rightarrow \text{E}( \dfrac{n}{n-1} S^2 ) = \sigma^2$$

در نتیجه $$S^2_{unb}$$ را برآورد نااریب برای واریانس جامعه آماری خواهیم یافت.

$$\large {\displaystyle S_{unb}^{2} = {\frac {1}{n-1} } \sum _{i=1}^{n} (X_{i} - {\overline {X}} \, )^{2} }$$

همانطور که دیدید، برای واریانس جامعه، برآوردگر اریب و نااریب وجود داشته و حتی می‌توان در بین برآوردگرهای اریب، برآوردگر کمترین واریانس را هم پیدا کرد.

برآوردگرهای میانه-نااریب

علاوه بر بحث برآوردگر اریب و نااریب، اصطلاح دیگری با عنوان برآوردگر میانه-نااریب نیز برای بعضی از برآوردگرها به کار گرفته می‌شود. تعریف و به کارگیری اصطلاح میانه-نااریب (Median-Unbiased) اولین بار توسط «جورج براون» (George Brown) آمارشناسی آمریکایی و استاد دانشگاه ایوا (Iowa State University) در سال ۱۹۴۷ مطرح شد. او برآوردگر میانه-نااریب را به صورت زیر تعریف کرد.

فیلم آموزش کاربرد رگرسیون و همبستگی در آمار استنباطی برای مدیریت و علوم انسانی (رایگان) در فرادرس

کلیک کنید

برآوردگر پارامتر تک بُعدی $$\theta$$ را میانه-نااریب گوییم، اگر برای مقدار ثابت $$\theta$$، میانه توزیع برآوردگر برابر با $$\theta$$ باشد. به این معنی که برآوردگر به همان میزانی که بیش‌برازش دارد، کم‌برازش هم داشته باشد. یکی از خصوصیات جالب برای چنین برآوردگری، ناوردا بودن (Invariant) تحت تبدیلات یک به یک (One-One Transformation) است.

این موضوع در مقابل مفهوم برآوردگر اریب و نااریب قرار گرفت. خوشبختانه در مواقعی که برآوردگر نااریب و حتی برآوردگر حداکثر درستنمایی وجود ندارند، می‌توان برآوردگر میانه-نااریب را بدست آورد. روش‌هایی مختلف برای ایجاد برآوردگرهای میانه-نااریب وجود دارد که در نوشتارهای دیگر فرادرس به آن‌ها اشاره خواهیم کرد.

خلاصه و جمع‌بندی

در این نوشتار با مفهوم برآوردگر اریب و نااریب به عنوان کلاسی از برآوردگرها آشنا شدیم. همانطور که خواندید، پیدا کردن بهترین برآوردگر از همه جنبه‌ها، کاری مشکل و شاید ناشدنی باشد. به همین دلیل در کلاسی از برآوردگرها که دارای خاصیت جالب یا بهینه‌ای هستند به دنبال بهترین برآوردگر هستیم. به این ترتیب در کلاس برآوردگرهای نااریب برآوردگرهای با کمترین واریانس از محبوبیت بیشتری برخوردارند. ولی ممکن است برآوردگر خارج از این کلاس نیز پیدا کرد که دارای واریانس کوچکتری از برآوردگر نااریب باشد. به همین دلیل بررسی و کنکاش در بین برآوردگر اریب و نااریب به آمارشناسان این امکان را می‌دهد که نسبت به انتخاب برآوردگر مناسب، دست به قضاوت بزنند.

اگر این مطلب برای شما مفید بوده است، آموزش‌ها و مطالبی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضی
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های آمار و احتمالات
• توزیع‌های آماری — مجموعه مقالات جامع وبلاگ فرادرس
• متغیر تصادفی و توزیع برنولی — به زبان ساده
• توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها

^^