تحلیل واریانس اندازه مکرر یک طرفه در SPSS | راهنمای گام به گام

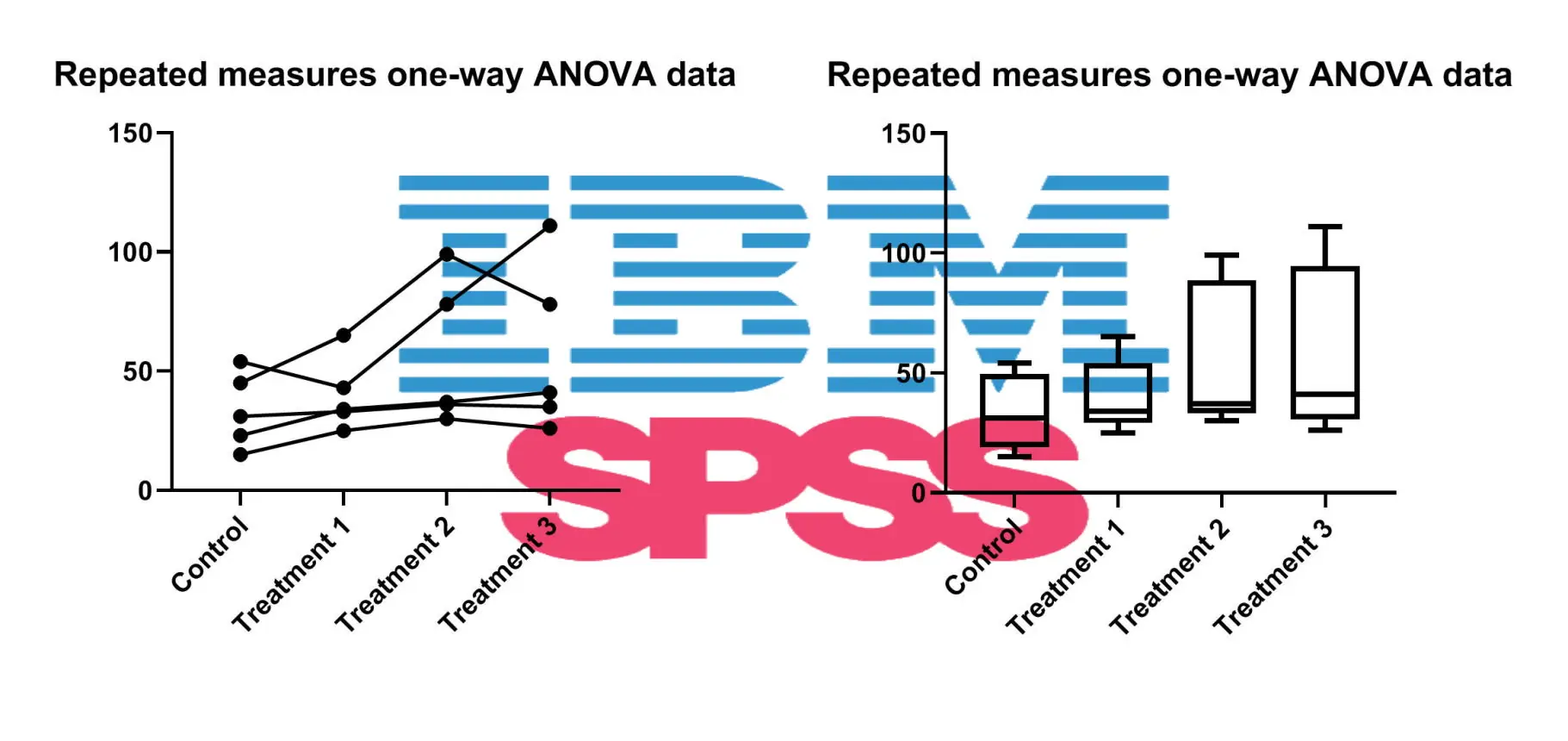
از تحلیل واریانس اندازه مکرر یک طرفه برای مقایسه میانگین سه یا چند گروه استفاده می‌شود که در آن شرکت کنندگان در همه گروه‌ها، مورد اندازه‌گیری قرار می‌گیرند. این تحلیل معمولاً در دو حالت یا وضعیت به کار می‌رود: (1) وقتی مشاهدات در زمان‌های متفاوت اندازه‌گیری می‌شوند تا تغییرات را در اثر یک مداخله (Intervention) مشخص کنند، (2) هنگامی که آزمودنی‌ها، در معرض بیش از یک تیمار/ شرایط آزمایشگاهی قرار گرفته و نتیجه یا پاسخ آن‌ها به شرایط باید مورد تحلیل قرار گیرد.

تحلیل واریانس اندازه مکرر را گاهی تحلیل واریانس با اندازه‌های تکراری نیز می‌نامند. در این متن برای دوری از محاسبات پیچیده و غیر ضروری و برای درک ساده‌تر موضوع به تحلیل واریانس اندازه مکرر یک طرفه (One-way Repeated Measures Analysis of Variance) خواهیم پرداخت. مشخص است که در اینجا فقط یک متغیر به عنوان فاکتور یا عامل به کار خواهد رفت و سطوح مختلف آن باعث ایجاد تیمار یا شرایط مختلف شده و گروه‌ها را تشکیل خواهد داد.

نرم‌افزارهای محاسبات آماری مختلفی، تحلیل واریانس اندازه مکرر را انجام می‌دهند و در این متن کار با نرم‌افزار SPSS را برای انجام این آزمون فرا خواهیم گرفت. البته ناگفته نماند که نحوه اجرای دستورات و گزارشات توسط این نرم‌افزار ساده و کامل بوده و نیازهای کاربران حرفه‌ای را هم برآورده می‌سازند.

به منظور آشنایی بیشتر با مفاهیم و روش کار در آنالیز واریانس اندازه مکرر بهتر است نوشتارهای دیگر مجله فرادرس با عنوان‌های آنالیز واریانس با مقادیر تکراری — از صفر تا صد و آنالیز واریانس (ANOVA) یک و دو طرفه در R — راهنمای کاربردی را مطالعه کنید. همچنین خواندن مطالب متغیر فاکتور (Factor) یا متغیر عامل در R — راهنمای کاربردی و تحلیل واریانس (Anova) — مفاهیم و کاربردها نیز خالی از لطف نیست.

تحلیل واریانس اندازه مکرر یک طرفه

اساس کار در تحلیل واریانس (Analysis of Variance) با به اختصار ANOVA، تجزیه تغییرات یا پراکندگی کل برحسب متغیر عامل گروه‌بندی (Between Group) و خطا (Error) است. البته در ANOVA با اندازه مکرر یک طرفه، پراکندگی خطا، خود به دو جزء دیگر به نام‌های «پراکندگی درون گروهی» (Within Group) و خطای مدل (Error)  تفکیک می‌شود. این امر باعث می‌شود که سطح خطای مدل، کاهشی باشد. به توجه به این موضوع، در صورتی که بین مشاهدات در سطوح مختلف یک عامل، وابستگی وجود داشته باشد، استفاده از ANOVA با اندازه مکرر نسبت به ANOVA یک طرفه ساده، برتری دارد زیرا طرح اجرا شده، دارای خطای کمتری است.

به عنوان مثال، می‌توانیم از یک تحلیل واریانس اندازه مکرر برای تحقیق در مورد سوال زیر استفاده کنیم.

• آیا در تعداد سیگار‌های مصرفی در بین سیگاری‌هایی که در یک برنامه ترک اعتیاد به کمک برچسب نیکوتین شرکت کرده‌اند، تفاوتی بوجود آمده است، یا خیر؟

در اینجا مدل آماری برای بیان اختلاف بین گروه‌ها را می‌توان به صورت زیر در نظر گرفت.

$$ \large y_{ij} = \tau_i + \varepsilon_{ij} , \;\;\; i = 1 , 2, \ldots , k , \;\;\; j = 1 , 2, \ldots , n_i $$

مدل طرح تحلیل واریانس اندازه مکرر یک طرفه

که $$y_{ij}$$ مشاهده $$j$$ام مربوط به متغیر وابسته برحسب تیمار یا گروه $$i$$ام است. در ضمن $$\tau_i$$ نیز میانگین متغیر وابسته در سطح $$i$$ام متغیر عامل محسوب می‌شود. واضح است که تعداد گروه‌ها برابر با $$k$$ و تعداد مشاهدات در گروه $$i$$ام نیز $$n_i$$ در نظر گرفته شده است. از طرفی می‌دانیم که مجموع $$n_i$$ها برابر با مقادیری اندازه‌گیری شده است. از طرفی باقی‌مانده‌ها یا جمله خطا ($$\varepsilon$$) نیز باید تصادفی بوده و دارای توزیع نرمال با میانگین صفر و واریانس $$\sigma^2$$ در هر یک از سطوح متغیر عامل باشند.

نکته: معمولا در جداول اطلاعاتی در نرم‌افزارهای محاسباتی، هر مشاهده را در یک سطر قرار می‌دهند. به همین علت چون یک آزمودنی (Subject) در بیش از یک سطح از متغیر عامل، اندازه‌گیری شده است، مقادیر متغیر وابسته برای آزمودنی را در یک سطر وارد می‌کنند. سطوح متغیر عامل در حقیقت مقادیر این سطر را مشخص خواهند کرد. در ادامه الگوی ورود داده‌ها برای ایجاد یک طرح آنالیز واریانس اندازه مکرر را معرفی و مورد بررسی قرار خواهیم داد.

در مثالی که گفته شد، مراحل یا مقاطع زمانی برای بررسی را می‌توانیم قبل از شرکت در برنامه ترک اعتیاد به منظور بهبود و کاهش مصرف سیگار، 10 ماه بعد و 26 ماه بعد در نظر بگیریم. در حقیقت به کمک آنالیز واریانس (ANOVA) با مقادیر تکراری، سعی داریم تغییرات متغیر پاسخ (متوسط تعداد سیگارهای مصرفی) را نسبت به مداخله (برنامه هیپنوتیزم) به عنوان متغیر عامل در سه سطح یا مقطع زمانی (تیمار)، بسنجیم و تغییر در متوسط سیگار مصرفی را در این سه مقطع مشخص کنیم. اگر متوسط تعداد سیگارهای مصرفی، کاهش داشته باشد، رای به موثر بودن مداخله خواهیم داد.

از طرف دیگر، می‌توانید از ANOVA با اندازه مکرر استفاده کنید تا تفاوت در سرعت شکستن شیشه جلو ماشین بر اساس سه رنگ مختلف را مشخص کنیم. در این بررسی، متغیر وابسته، سرعت شکستن (برحسب میلی ثانیه) و متغیر مستقل نوع شیشه پنجره است. به عنوان مثال نوع شیشه می‌تواند در حالت‌ها  بدون روکش رنگی ، روکش رنگی نازک، روکش رنگی متوسط ​​و روکش رنگی ضخیم، در نظر گرفته شود و متوسط سرعت شکستن هر یک از این حالت‌ها، مورد بررسی قرار گیرد.

نکته: آنالیز واریانس اندازه مکرر یک طرفه، زمانی استفاده می‌شود که فقط یک متغیر عامل (متغیر مستقل) در مدل حضور دارد. اگر تعداد متغیرهای عامل بیش از یک متغیر باشد (دو یا بیشتر)، آنالیز واریانس را دو طرفه (Two -way) یا چند طرفه (Multi-way) می‌نامند.

در این متن به بررسی نحوه اجرای تجزیه و تحلیل واریانس اندازه مکرر یک طرفه در محیط SPSS خواهیم پرداخت. در این بین فرضیاتی که برای اجرای آزمون لازم است نیز معرفی شده و توسط SPSS مورد تحلیل قرار خواهند گرفت. البته توجه داشته باشید که نسخه نرم‌افزار به کار رفته در این متن SPSS 26 است. به این ترتیب اگر از نسخه دیگر این نرم‌افزار استفاده می‌کنید، ممکن است بعضی از تنظیمات آن با تصویرهای به کار رفته تفاوت داشته باشند. ولی به هر حال نتایج و جدول‌های تولید شده مشابه و یکسان هستند.

پیش‌فرض‌های آماری برای تحلیل واریانس اندازه مکرر یک طرفه

در هر روش آماری، پیش‌نیازها یا پیش‌فرض‌هایی وجود دارد که بدون در نظر گرفتن صحت آن‌ها ممکن است نتیجه حاصل از تجزیه و تحلیل آماری، بی‌اعتبار باشند. در تحلیل واریانس اندازه مکرر یک طرفه نیز چنین پیش‌فرض‌هایی وجود دارد. البته ممکن است بررسی صحت بعضی از این فرض‌ها بعد از اجرای تحلیل واریانس نیز صورت بگیرد، ولی حتی در این صورت نیز اعتبار تحلیل انجام شده به برقراری چنین پیش‌نیازهایی وابسته است.

در ادامه به ۵ شرط اصلی در تحلیل واریانس اندازه مکرر یک طرفه خواهیم پرداخت که البته بعضی از آن‌ها را در محیط SPSS نیز می‌توان مورد بررسی قرار داد.

نکته: هنگام کار روی داده‌های مربوط به مسائل دنیای واقعی (نه محیط و شرایط ایده‌آل)، اغلب همه شرط‌های گفته شده محقق نمی‌شوند. ولی برای چنین حالت‌هایی نیز راه‌ حل‌هایی نظیر تغییر متغیر، تبدیل و نرمال‌سازی داده‌ها، استفاده از «روش‌های ناپارامتری» (Non-parametric Methods) می‌تواند راه حلی برای مسئله شما ارائه کنند.

پیش‌فرض شماره 1: کمی بودن متغیر وابسته

متغیر وابسته شما باید یک متغیر پیوسته (کیفی) یعنی متغیرهای از نوع «فاصله‌ای» (Interval) یا «نسبی» (Relative) باشد. نمونه‌هایی از متغیرهای پیوسته عبارتند از: «زمان» (اندازه گیری شده برحسب ثانیه یا ساعت)، «هوش» (اندازه‌ ضریب هوشی)، «کارایی در آزمون» (نمره آزمون از ۰ تا ۱۰۰)، «وزن» (برحسب گرم یا کیلوگرم) و غیره. به منظور آشنایی بیشتر با مقیاس‌های اندازه‌گیری داده‌ها بهتر است نوشتار جامعه آماری – انواع داده و مقیاس‌های آن‌ها را مطالعه کنید.

پیش‌فرض شماره 2: تعداد سطوح متغیر مستقل

متغیر مستقل شما باید حداقل از دو گروه یا طبقه تشکیل شده باشد. به علت وابستگی بین مقادیر در هر طبقه، آن‌ها را «گروه‌های مرتبط» (Related Groups) یا «زوج همسان» (Matched Pairs) نیز می‌نامند.

نکته: گاهی برای انجام آنالیز واریانس اندازه مکرر از افراد دو قلو یا همسان استفاده می‌شود و هر یک از قل‌ها را در یک گروه قرار داده و مقدار متغیر وابسته را اندازه‌گیری می‌کنند. از آنجایی که دوقلوهای همسان، رفتار و خصوصیات مشابهی دارند، تغییر در نتایج فقط در اثر متغیر عامل یا مداخله کننده روی خواهد داد.

«گروه‌های مرتبط» نشان می‌دهند که مشاهداتی با خصوصیات یکسان در هر گروه وجود دارد. دلیل این امر، امکان اندازه‌گیری متغیر وابسته در هر سطح از متغیر عامل روی آزمودنی‌ها است. به این ترتیب متغیر وابسته روی هر فرد به تعداد سطوح متغیر عامل، اندازه‌گیری می‌شود.

به عنوان مثال، ممکن است عملکرد 10 نفر را در یک آزمون املا (متغیر وابسته) قبل و بعد از اجرای روش آموزش رایانه‌ای، اندازه‌گیری کنیم. علاقمند هستیم تاثیر روش آموزش رایانه‌ای را روی عملکرد املا مشخص کنیم. به این ترتیب نتایج حاصل از تحلیل واریانس اندازه مکرر یک طرفه پاسخ مناسبی به سوال ما خواهد داد.

در این جا، گروه‌ها از دو مولفه تشکیل شده است. مولفه اول، فرد را در گروه اول، یعنی قبل از استفاده برنامه آموزشی رایانه‌ای مشخص می‌کند و مولفه دوم نیز او را در گروه بعد از آزمایش قرار می‌دهد. نمره املاء این فرد در هر یک از این دو حالت به عنوان متغیر پاسخ ثبت می‌شود و مقدار مولفه‌ها را مشخص می‌کند.

پیش‌فرض شماره 3: حذف نقاط پرت در مشاهدات

در «گروه‌های مرتبط» نباید «نقاط پرت» (Outliers) وجود داشته باشند. در صورت وجود چنین نقطه‌هایی، مدل ارائه شده دچار مشکل شده و برآورد درستی ارائه نخواهد داد. به عنوان مثال، وضعیتی را در نظر بگیرید که در یک طرح مطالعاتی از 100 نمره ضریب هوشی دانش آموزان که میانگین امتیاز آن 108 بوده و واریانس یا انحراف معیار بین نمرات بسیار اندک است. به این ترتیب به نظر می‌رسد که کلاس، همگن باشد. ولی یکی از دانش آموزان نمره 156 برای ضریب هوشی داشته که بسیار غیر معمول است. به این ترتیب باید او را در سطح 1٪ از نمرات ضریب هوشی در سطح جهان قرار دهیم.

نکته: البته ممکن است نمره او به لحاظ بی‌دقتی در ورود اطلاعات به این صورت ثبت شده باشد. با بررسی بیشتر می‌توان این داده پرت را مورد تحلیل قرار داد تا از صحت اطلاعات ذخیره شده، اطمینان پیدا کرد.

مشکلی که حضور چنین فردی در طرح تحقیقی ایجاد می‌کند، این است که نمره او می‌تواند تأثیر منفی بر روی ANOVA اندازه مکرر داشته باشد و اختلافات بین گروه‌های مرتبط (اعم از افزایش یا کاهش نمرات در متغیر وابسته) را تحریف کند. می‌دانیم که میانگین به شدت به نقاط پرت حساس است و این امر باعث تغییر در تجزیه مجموع مربعات (Sum of Squares) پراکندگی یا تغییرات، خواهد شد.

خوشبختانه، هنگام استفاده از نرم‌افزار آماری SPSS در تحلیل ANOVA، می‌توانیم حضور چنین نقاط یا مشاهداتی را مورد بررسی قرار دهیم.

پیش‌فرض شماره 4: توزیع نرمال برای متغیر وابسته (عبارت خطا)

در تحلیل واریانس اندازه مکرر توزیع متغیر وابسته در هر گروه مرتبط، باید «توزیع نرمال» (Normal Distribution) یا تقریبا نرمال باشد.

ولی اگر فرض مربوط به «آزمون نرمال بودن» (Normality Test) توسط این آزمون‌ها رد شود، اما میزان «چولگی» (Skewness) و «کشیدگی» (Kurtosis) منحنی توزیع داده‌ها زیاد نبوده و قابل چشم‌پوشی باشد، باز هم می‌توان از روش آنالیز واریانس اندازه مکرر استفاده کرد.

برازش توزیع برای مقادیر متغیر وابسته با توزیع نرمال توسط آزمون‌های مختلفی در محیط SPSS قابل اجرا است. برای برازش توزیع متغیر وابسته با توزیع نرمال می‌توانید از آزمون نرمال بودن «شاپیرو- ویلک» (Shapiro-Wilk)، که به راحتی قابل دسترس است، بهره ببرید. همچنین از آزمون کولموگروف-اسمیرنوف (Kolmogorov-Smirnov) و از روش تصویری نظیر نمودار چندک-چندک یا Q-Q plot‌ نیز می‌توان برای برازش توزیع نرمال، بهره برد.

پیش‌فرض شماره 5: فرض کرویت گروه‌ها

واریانس مقادیر متغیر وابسته در بین گروه‌ها باید در هر یک از سطوح متغیر عامل یا گروه‌ها، ثابت و برابر باشد. این فرض در آنالیز واریانس اندازه مکرر به نام فرض «کرویت» (Sphericity) شناخته می‌شود. یکی از تکنیک‌های تشخیص کرویت، استفاده از آزمون و «آماره موچلی» (Mauchly’s Statistics) است.

متاسفانه ANOVA با مقادیر تکراری نسبت به صحت و برقراری این شرط بسیار حساس است. اگر واریانس گروه‌ها برابر نباشد، آماره مورد استفاده برای این آزمون باید تجدید نظر شده و به شکل دیگری محاسبه شود. ولی خوشبختانه شیوه بررسی فرض کرویت در نرم‌افزار SPSS لحاظ شده و یکی از اصلی‌ترین خروجی‌های تحلیل واریانس اندازه مکرر را تشکیل می‌دهد.

در ادامه شرط کرویت را در طی تحلیل واریانس اندازه مکرر یک طرفه در SPSS، با ذکر یک مثال مورد بررسی قرار داده و خروجی حاصل را نیز تفسیر خواهیم کرد.

نکته: واضح است که صحت و بررسی برقراری فرض‌های اول و دوم به عهده کاربر است و نرم‌افزار SPSS برای سنجش آن ابزاری ندارد. ولی فرضیات شماره ۳، ۴ و ۵ توسط نرم‌افزار قابل بررسی و سنجش هستند. در این متن روش‌های بررسی این فرضیات نیز مورد بررسی قرار می‌گیرد.

بخاطر داشته باشید که اگر آزمون‌های آماری را روی این فرضیات به درستی اجرا نکنید، ممکن است نتایج ANOVA با اندازه مکرر دارای اعتبار کافی نباشند و مدل ارائه شده قابلیت تعمیم به جامعه آماری را ندارد.

در ادامه یک مثال را برای آشنایی با گام‌های ANOVA با اندازه مکرر ارائه می‌کنیم و در مورد صحت فرضیات برای نتیجه حاصل در SPSS، بحث خواهیم کرد.

حل یک مسئله تحلیل واریانس اندازه مکرر یک طرفه در SPSS

یک محقق در عرصه آموزشی می‌خواهد اثر سر و صدا در محیط آموزش روی تمرکز و به خاطر سپردن را در بین افراد بسنجد. او از یک آزمایش طرح‌ریزی شده استفاده می‌کند که در آن ۲۰ دانش آموز در چهار حالت یا سطح از سر و صدا مورد آزمایش قرار می‌گیرند. به هر یک از این دانش آموزان یک لیست از کلمات داده می‌شود تا آن را به خاطر بسپرند. تعداد کلماتی که هر یک از آن‌ها در سطوح مختلف سر و صدا به خاطر سپرده‌اند، متغیر وابسته در نظر گرفته می‌شود. او می‌خواهد با انجام این آزمایش، نقش سر و صدای محیطی را در قدرت تمرکز ارزیابی کند. در حقیقت با اجرای این طرح آزمایش‌ها می‌خواهد به این سوال پاسخ دهد که آیا محیط‌های پر سر و صدا باعث کاهش تمرکز می‌شوند یا خیر؟

در دستورالعمل‌های که در ادامه مطرح خواهیم کرد، گام‌های مربوط به اجرای این طرح را در SPSS معرفی کرده و نتایج نهایی را براساس یک نمونه فایل اطلاعاتی SPSS، تفسیر می‌کنیم.

به منظور دسترسی به فایل اطلاعاتی SPSS کافیست روی اینجا کلیک تا فایل noisedata.sav را با قالب فشرده دریافت کنید. بدیهی است، پس از خارج کردن این فایل از حالت فشرده می‌توانید آن را در SPSS و پنجره ویرایشگر داده (Data Editor) بارگذاری کرده و عملیات بعدی را انجام دهید. همچنین توجه داشته باشید که نتایج اجرای این دستورات، در پنجره خروجی (SPSS Output) قرار خواهند گرفت.

بهتر است ابتدا نگاهی به این مجموعه داده بیاندازیم تا با متغیرها و مقادیر آن بیشتر آشنا شویم. در تصویر ۱، دو پنجره ویرایشگر داده در نمای داده (Data View)، (سمت چپ) و نمای متغیرها (Variable View)، (سمت راست) دیده می‌شوند.

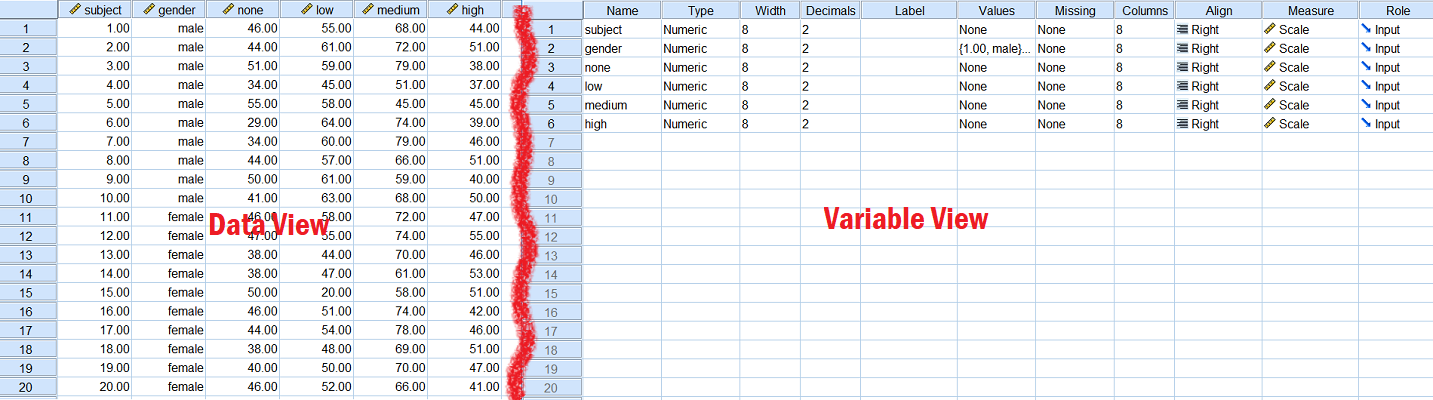
واضح است که ۲۰ مشاهده موجود بوده که از آن‌ها، چهار بار در سطوح مختلف سر و صدا، آزمایش صورت گرفته است. متغیرهای «جنسیت» (Gender) و «شماره آزمودنی» (Subject) در این متن مورد بررسی قرار نخواهند گرفت.

متغیر عامل در اینجا به صورت سطوح مختلف سر و صدا و با اسامی none ،low ،medium ،high معرفی شده‌اند. مقادیری که برای این ستون‌ها ثبت شده، تعداد کلماتی است که هر یک از آزمودنی‌ها (افراد شرکت کننده در تحقیق) در هر یک از محیط‌ها به خاطر آورده‌اند. در حقیقت هر ستون نشانگر یک نوع تیمار/شرایط است و مقادیر ستون‌ها نیز متغیر وابسته را مشخص می‌کنند.

در ادامه هر یک از مراحل اجرای کار و تفسیر خروجی‌ها را به صورت گام به گام شرح و توضیح خواهیم داد.

گام ۱: اجرای تحلیل واریانس اندازه مکرر یک طرفه

دستور مربوط به اجرای تحلیل واریانس اندازه مکرر را از طریق مسیر زیر اجرا کنید. البته تصویر 2 نیز دسترسی به این دستور را نشان داده است.

 Analyze > General Linear Model > Repeated Measures…

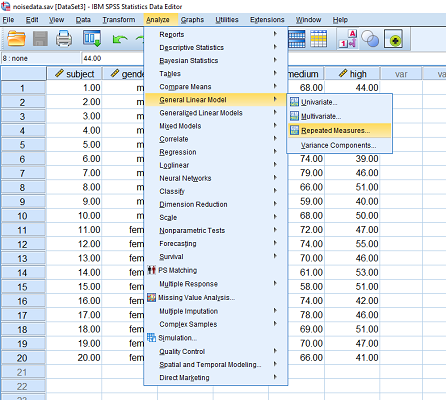
با اجرای این گام، پنجره مربوط به انتخاب متغیر عامل و سطوح آن ظاهر می‌شود.

گام ۲: تعیین سطوح متغیر عامل

از آنجایی که در این تحلیل چهار ستون none ،low ،medium ،high، سطوح مختلف متغیر عامل را مشخص می‌کنند، پنجره تعریف این متغیر را به مانند تصویر ۳، تنظیم می‌کنیم.

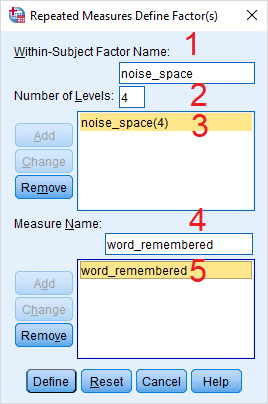
در قسمت Within-Subject Factor Name، نام متغیر عامل را (noiseـspace) مشخص کرده‌ایم. تعداد سطوح متغیر عامل را هم در کادر Numbers of Levels برابر با ۴ در نظر گرفته و در قسمت Measure Name نیز متغیر وابسته را (word_remembered) نام‌گذاری کرده‌ایم. بعد از معرفی هر یک از متغیرها با فشردن دکمه Add، متغیرها را به کادر پایین انتقال داده تا عمل تعریف متغیرها کامل شود.

نکته: برای تغییر یا حذف اسامی متغیرها کافی است پس از انتخاب آن‌ها، از دکمه Change یا Remove استفاده کنید.

با فشردن دکمه Define متغیرهای عامل و متغیر وابسته را در پنجره Repeated Measures برای مدل آنالیز واریانس اندازه مکرر معرفی خواهیم کرد.

در این پنجره کافی است هر یک از ستون‌هایی که به عنوان عامل معرفی شده‌اند را انتخاب کنید و با فشردن دکمه → آن را به کادر Within-Subjects Variables بکشید.

واضح است که بنا به نام‌گذاری انجام شده در پنجره قبلی، نام این قسمت noise-space است. نتیجه اجرای این تنظیمات در تصویر ۴ دیده می‌شود.

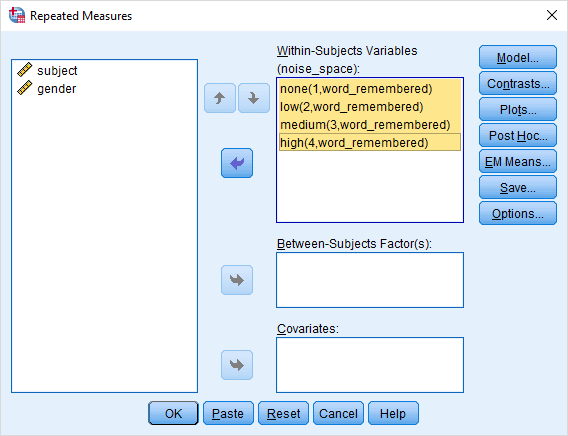
گام ۳: رسم نمودار مقایسه‌ای (Profile Plots)

اگر دوست دارید که میانگین هر چهار گروه در یک نمودار خطی با یکدیگر مقایسه شوند، دکمه Plots را کلیک کنید و متغیر عامل را به کادر مربوط به محور افقی (Horizontal Axis) ببرید، سپس دکمه Add را بزنید. این کار را در تصویر 5 مشاهده می‌کنید.

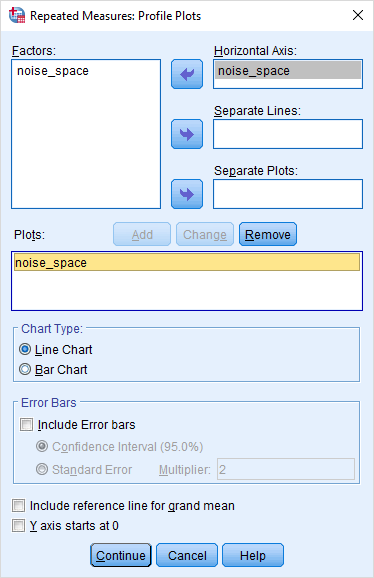
نکته: اگر بخواهید به جای «نمودار خطی» (Line Chart)، یک «نمودار میله‌ای» (Bar Chart) ترسیم شود، باید از قسمت Chart Type گزینه Bar Chart را انتخاب کنید.

با فشردن دکمه Continue به پنجره قبلی باز خواهید گشت.

گام ۴: مقایسه‌های دو تایی و میانگین حاشیه‌ای

تحلیل واریانس اندازه مکرر فقط تعیین می‌کند که آیا میانگین در سطوح مختلف متغیر عامل برابرند یا خیر. ولی نمی‌تواند تحلیلی در سطح گروه‌ها برای تشخیص سطحی از عامل که باعث نابرابری شده ارائه دهد. این کار را بواسطه انتخاب گزینه EM Means می‌توان انجام داد.

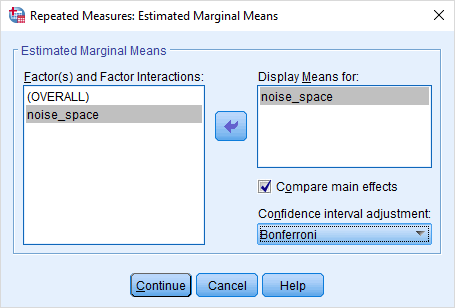
برای مقایسه‌های دو تایی بین گروه‌ها و تعیین سطح عاملی که باعث رد فرض صفر (برابری میانگین در بین چهار گروه) شده، در بخش Factor(s) and Factor Interactions، متغیر noise_space را به کادر Display means for انتقال می‌دهیم و گزینه Compare main effects را هم انتخاب می‌کنیم. به این ترتیب مقایسه‌های دو تایی بین گروه‌ها توسط تکنیک «بونفرونی» (Bonferroni) صورت خواهد گرفت.

تنظیمات صورت گرفته در این پنجره، در تصویر ۶ قابل مشاهده‌اند.

گام ۵: تغییر تنظیمات پیش‌فرض

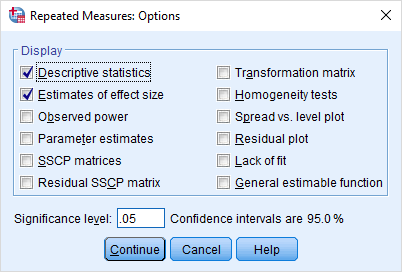
خروجی‌هایی که دستور آنالیز واریانس با مقادیر تکراری در SPSS اجرا می‌کند، پیش‌فرض‌ها یا تنظیمات اولیه دارد که در پنجره Options قابل تغییر است. کافی است در پنجره اصلی این دستور یعنی Repeated Measures، دکمه Options را کلیک کنید تا پنجره‌ای مطابق با تصویر 7 مشاهده کنید.

برای آنکه بتوانیم محاسبات مربوط به آمار توصیفی را در پنجره خروجی برای هر گروه دریافت کنیم، در بخش Display گزینه Descriptive statistics را انتخاب خواهیم کرد. همچنین برای مشخص شدن «اندازه اثر» (Effect size) نیز گزینه «برآورد اندازه اثر» (Estimates of effect size) را کلیک می‌کنیم. به این ترتیب برای متغیر عامل اندازه اثر محاسبه خواهد شد.

با فشردن دکمه Continue به پنجره اصلی این فرمان باز خواهیم گشت. البته گزینه‌های دیگری نیز برای اجرای این دستور وجود دارد که از حوصله این مطلب خارج هستند. به هر حال به کمک گزینه‌های انتخاب شده، هدف از اجرای آزمون محقق خواهد شد.

نکته: اگر می‌خواهید این دستور و تنظیمات آن را در محیط کد نویسی SPSS یعنی پنجره Syntax اجرا کنید، از دستورات زیر استفاده کنید.

DATASET ACTIVATE DataSet1.
GLM none low medium high
  /WSFACTOR=noise_space 4 Polynomial 
  /MEASURE=word_remembered 
  /METHOD=SSTYPE(3)
  /PLOT=PROFILE(noise_space) TYPE=LINE ERRORBAR=NO MEANREFERENCE=NO YAXIS=AUTO
  /EMMEANS=TABLES(noise_space) COMPARE ADJ(BONFERRONI)
  /PRINT=DESCRIPTIVE ETASQ 
  /CRITERIA=ALPHA(.05)
  /WSDESIGN=noise_space.

به این ترتیب با طی کردن این پنج گام یا مرحله، با فشردن دکمه OK در پنجره اصلی این فرمان، خروجی‌ها ظاهر شده و نتایج را در پنجره Output مشاهده خواهید کرد. در بخش بعدی به معرفی و تفسیر خروجی‌های حاصل خواهیم پرداخت.

تفسیر خروجی‌های تحلیل واریانس اندازه مکرر در SPSS

در تحلیل واریانس اندازه مکرر، نرم‌افزار SPSS جدول‌های متعددی را در خروجی تولید می‌کند. این بخش به توصیف نتایج حاصل اختصاص دارد. در این بین شرط یا فرض‌هایی که برای صحت انجام عملیات گفتیم نیز مورد بازبینی قرار خواهند گرفت. خروجی و نتایج حاصل را به چهار بخش تفکیک کرده و در ادامه مورد بحث قرار می‌دهیم.

بخش اول: آمار توصیفی و معرفی متغیرهای مربوط به تحلیل

در تصویر 8، خروجی حاصل این بخش را مشاهده می‌کنید. واضح است که در جدول Within-Subjects Factors، متغیر وابسته یا اندازه همان word_remembered نامیده شده که در سطوح مختلف متغیر noise_space اندازه‌گیری شده است.

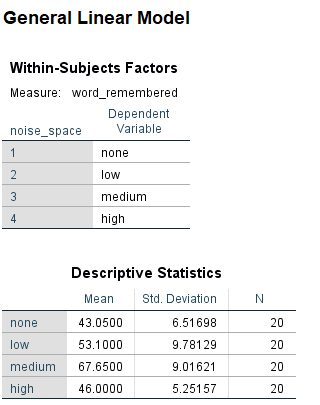
در جدول Descriptive Statistics نیز میانگین (Mean) و انحراف معیار (Std. Deviation) برای متغیر وابسته (تعداد کلمات به خاطر سپرده شده) در هر یک از سطح‌های متغیر عامل (محیط‌های پر سر و صدا) محاسبه و نمایش داده شده است. همچنین در ستون آخر (N) نیز تعداد مشاهدات در هر سطح دیده می‌شود.

نکته: واضح است که این طرح، یک طرح کامل و متوازن است، زیرا تعداد مشاهدات در همه سطوح برابر هستند.

همانطور که می‌بینید، تقریبا در هر یک از سطوح، تفاوت در میانگین به چشم می‌خورد ولی از آنجایی که واریانس‌ها متفاوت هستند، ممکن است این تفاوت‌ها از لحاظ آماری معنی‌دار نباشند. به همین علت دست به اجرای آزمون تحلیل واریانس اندازه مکرر زده‌ایم.

بخش دوم: نتایج اجرای آزمون

در بخش بعدی، نتایج آزمون طی یک جدول به نام Multivariate Tests ظاهر شده است. براساس این جدول و ستون Sig می‌توان، فرض صفر (یعنی برابری میانگین طی تیمارها) را رد کرد. زیرا مقدار Sig کوچکتر از حداقل احتمال خطای نوع اول ($$0.05$$) شده است. در نتیجه همه آماره‌های آزمون شامل «اثر پیلای» (Pillai’s Trace)، «لاندای ویلک» (Wilk’s Lambda)، «اثر هوتلینگ» (Hoteling’sTrace) و «بزرگترین ریشه روی» (Roy’s Largest Root) نیز رای به رد فرض صفر می‌دهند.

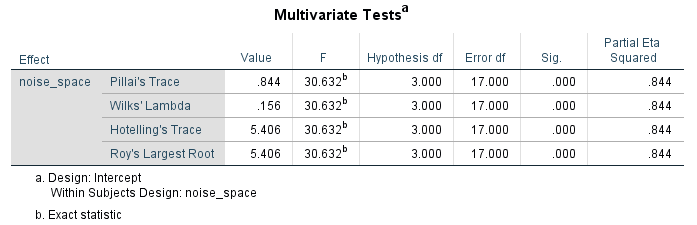
در ستون آخر مربوط به جدول نمایش داده شده در تصویر ۹ نیز اندازه اثر (Effect Size) براساس «مربع اتای جزئی» (Partial Eta Squared) بدست آمده است.

بخش سوم: تحلیل دو به دو و میانگین حاشیه‌ای

جدول آنالیز واریانس (ANOVA) یکی از مهم‌ترین خروجی‌های حاصل از تحلیل واریانس است. ولی قبل از آن باید از وضعیت «کرویت واریانس‌ها» اطلاع کسب کنیم. به این منظور نرم‌افزار محاسبات آماری SPSS با استفاده از «آزمون موچلی» (Mauchly’s Sphericity Test)، فرض کرویت را مورد بررسی قرار می‌دهد. براساس مثال ما و تصویر 10، مشخص می‌شود که این فرض رد نشده و می‌توان کرویت در واریانس‌ها را برای مدل تحلیل واریانس در نظر گرفت.

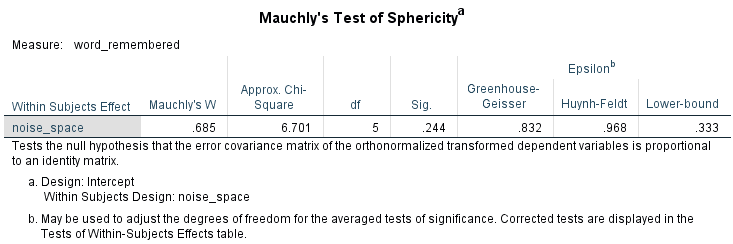
نکته: فرض صفر در این آزمون بیانگر برابری ماتریس کوواریانس متغیر وابسته (در سطوح مختلف متغیر عامل) با مضربی از «ماتریس یکه» (Identity Matrix) است. با توجه به این که دلیلی بر رد فرض صفر با توجه به نمونه داده شده وجود ندارد، فرض کرویت را نمی‌توانیم رد کنیم.

بخش چهارم: جدول آنالیز واریانس اندازه مکرر و ترکیب سطوح متغیرهای عامل

بخش بعدی از خروجی، مرتبط با جدول آنالیز واریانس (ANOVA) براساس رد یا قبول فرض کرویت است. اگر فرض کرویت در آزمون موچلی، مورد قبول واقع شود، سطر اول جدول Tests of Within-Subjects Effects را مطابق با تصویر ۱۱، در نظر می‌گیریم. در غیر این صورت سطرهای بعدی نظیر «آماره گرینهاوس-گیسر» (Greenhouse-Geisser) مورد توجه قرار می‌گیرد. مطابق با ستون مربوط به Sig برای همه آماره‌های آزمون اثرات درون گروهی، فرض صفر رد شده و تاثیرگذاری سطوح متغیر عامل روی متغیر وابسته به خوبی مشخص می‌شود.

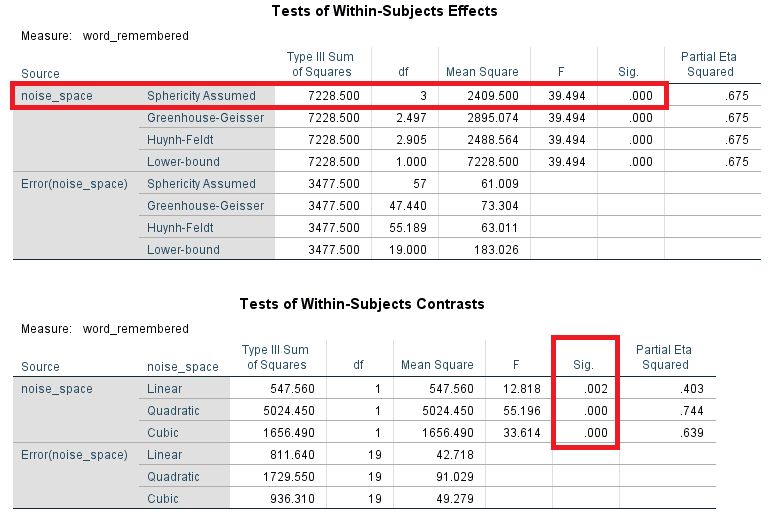
از طرفی روند تغییرات میانگین در سطوح مختلف متغیر عامل را می‌توان یک ترکیب خطی (Linear)، مربعی (Quadratic) یا مکعبی (Cubic) در نظر گرفت. مطابق با جدول (Tests of Within-Subjects Contrasts)، هیچ یک از این الگوها برای روند تغییرات میانگین پذیرفته نشده و همگی آن‌ها رد خواهند شد. البته بهتر است برای تایید این امر، به نموداری که در انتهای خروجی ظاهر شده نیز نگاهی بیندازیم. ابتدا به نظر می‌رسید که هر میزان افزایش در سطح سر و صدا باعث کاهش کلماتی شود که به خاطر می‌سپاریم، ولی مدل ایجاد شده چنین اثری را مشخص نمی‌کند. به این ترتیب هیچ یک از مدل‌های چند جمله‌ای معرفی شده، با معنی نشده‌اند.

بخش پنجم: مقایسه‌های دو تایی برای میانگین‌ها

اگر به دنبال مقایسه‌های دو به دو یا زوجی هستید، جدول بعدی به کار می‌آید. البته به علت اینکه گزینه مربوط به «برآورد میانگین‌های حاشیه‌ای» (Estimated Marginal Mean) را انتخاب کرده بودیم، گزینه‌های این قسمت به عنوان خروجی ظاهر شده‌اند. در ابتدای این بخش «میانگین» (Mean)، «خطای استاندارد» (Std. Error) و «فاصله اطمینان» (Confidence Interval) با سطح اطمینان ۹۵٪ برای میانگین متغیر وابسته در هر سطح از متغیر عامل را مشاهده می‌کنید.

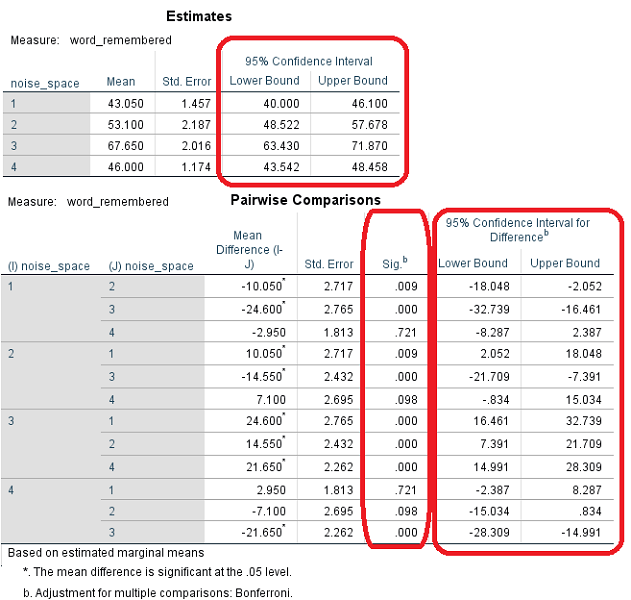
در انتهای این بخش و در پایین تصویر ۱۲، میانگین متغیر وابسته در هر سطح از متغیر عامل با سطوح دیگر به صورت مقایسه‌های زوجی مورد آزمون قرار گرفته و نتایج مربوط به آن نمایش داده شده است. همانطور که در ستون Sig مشاهده می‌کنید، محیط بدون کنترل سر و صدا (None) با هر یک از محیط‌های دیگر (شامل low noise و Mid Noise) تفاوت معنی‌داری دارد. ولی با توجه به Sig=.721، مشخص است که بین گروه اول و چهارم، تفاوت معنی‌داری دیده نمی‌شود ولی دو گروه بعدی با این دو گروه، تفاوت معنی‌داری دارند.

این موضوع را به کمک فاصله اطمینان ۹۵٪ نیز می‌توان درک کرد. واضح است که هر یک از فاصله‌های اطمینان که شامل نقطه صفر باشند، فرض صفر را رد نمی‌کنند. بنابراین نتایج قبلی این بار هم تایید می‌گردند.

بخش ششم: نمودار روند تغییرات میانگین متغیر وابسته

در این قسمت با استفاده از نموداری که برای مقایسه روند تغییرات میانگین متغیر وابسته در سطوح مختلف متغیر عامل ترسیم شده است، می‌توانیم الگوی مشخصی را تعیین کنیم. در حالت اول، بدون آنکه روی سر و صدا، کنترلی صورت گیرد آزمایش را انجام داده‌ایم. تعداد کلماتی که شرکت‌کنندگان به خاطر سپرده‌اند از دو حالت سر و صدای کم و متوسط، کمتر است و درست زمانی که سر و صدا افزایش می‌یابد، تعداد کلمات به خاطر سپرده شده، کاهش یافته و در حد محیط کنترل نشده خواهند بود.

به همین علت الگو در سطوح مختلف متغیر عامل، به صورت یک الگوی غیر خطی و بدون الگوی چند جمله‌ای درجه دوم یا سوم در آمده است. این موضوع نیز در جدول Contrast (تصویر 11)، مشاهده شد. در آنجا دیدیم که هیچ یک از الگوهای چند جمله‌ای معرفی شده معنی‌دار نبودند. نمودار خطی (Line Chart) را در تصویر ۱۳ مشاهده می‌کنید. نمودار ترسیم شده نیز این موضوع را تایید می‌کنند.

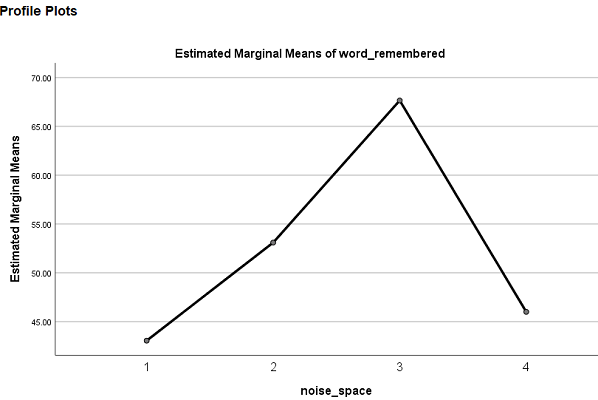
در نهایت با توجه به خروجی‌های ایجاد شده، مشخص شده که فرض صفر در تحلیل واریانس اندازه مکرر یک طرفه رد شده و می‌توان گفت که نوع محیط در کارایی حافظه دخالت دارد. جالب است که در محیط با سر و صدای متوسط، بیشترین کارایی از لحاظ تعداد کلمات به خاطر سپرده شده، وجود دارد.

آزمون تصادفی و نرمال بودن باقیمانده‌ها

همانطور که گفته شد، پیش‌فرض‌های سوم و چهارم نیز برای اعتبار مدل یا تحلیل ارائه شده باید مورد بازبینی قرار گیرند. برای هر دو این پیش‌فرض‌ها، احتیاج به باقی‌مانده‌های حاصل از تحلیل واریانس اندازه مکرر داریم. به این منظور بهتر است یکبار دیگر به پنجره Repeated Measures بازگردیم و از دکمه Save، برای ذخیره سازی باقی‌مانده (یا خطای مدل) استفاده کنیم. در تصویر ۱۴، چنین کارهایی در این پنجره صورت گرفته است.

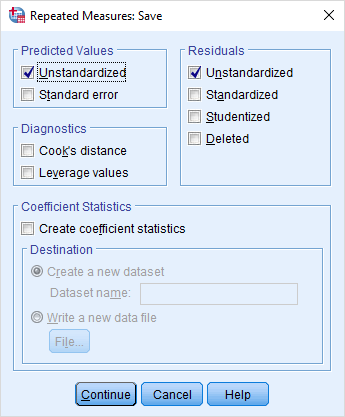
کافی است در بخش Residuals گزینه، Unstandardized یا «باقی‌مانده‌های استاندارد نشده» را انتخاب کنید. البته ما در تصویر 14 این کار را برای «متغیر پیش‌بینی» (Predicted Values) نیز انجام داده‌ایم. به این ترتیب دو گروه متغیر جدید به نام‌های PRE1 تا PRE4 و RES1 تا RES4، ایجاد می‌شوند. برای مقدار پیش‌بینی هر یک از مقادیر متغیر وابسته اسامی PRE1 تا PRE4 به کار رفته و متناظر با آن‌ها نیز باقی‌مانده‌ها در متغیرهای RES1 تا RES4 قرار می‌گیرند.

واضح است که میانگین محاسبه شده در هر یک از سطوح، به عنوان مقدار پیش‌بینی شده، ظاهر می‌شوند، زیرا طبق مدلی که در ابتدای متن برای تحلیل واریانس اندازه مکرر معرفی کردیم، میانگین به عنوان مقدار متوسط متغیر وابسته در نظر گرفته شده بود.

در تصویر ۱۵، نتیجه محاسبه این متغیرهای جدید را در پنجره ویرایشگر داده (Data Editor)‌ مشاهده می‌کنید. به مقدار پیش‌بینی شده نیز توجه داشته باشید.

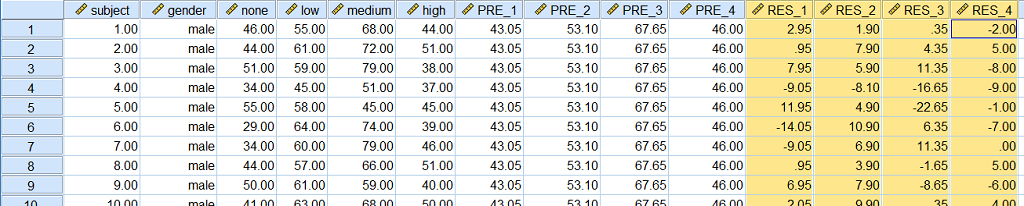
نکته: با اضافه کردن این گزینه‌ها و اجرای دستورات، مجددا خروجی‌های قبلی نیز تولید شده و در پنجره Output قرار خواهند گرفت.

با توجه به مدل ارائه شده برای تحلیل واریانس یک طرفه که در ابتدای متن به آن اشاره شد، مشخص است که باقی‌مانده‌ها چگونه محاسبه می‌شوند. کافی است هر یک از مقادیر مشاهده شده را از برآورد آن کم کنیم. در واقع از تفاضل هر مقدار پیش‌بینی و مقدار واقعی، باقی‌مانده بدست می‌آید. از طرفی مقادیر حاصل (باقی‌مانده‌ها) باید دارای توزیع نرمال باشند. وجود داده پرت یا دور افتاده نیز می‌تواند توسط تحلیل روی مقدارهای باقی‌مانده صورت می‌پذیرد.

باقی‌مانده‌ها نیز به راحتی به کمک روش‌هایی که برای شناسایی «نقاط پرت» (Outliers) در نوشتارهای دیگر مجله فرادرس منتشر شده، قابل ارزیابی هستند. همچنین نرمال بودن نیز به راحتی توسط آزمون «شاپیرو- ویلک» (Shapiro-Wilk) مورد بررسی قرار می‌گیرد. از آنجایی که در مورد این دو موضوع و آزمون‌های مرتبط، در مجله فرادرس مطلب‌های زیادی منتشر شده است از بازگویی آن‌ها در اینجا خودداری می‌کنیم.

خلاصه و جمع‌بندی

همانطور که خواندید، این متن به نحوه اجرای تحلیل واریانس اندازه مکرر یک طرفه در SPSS اختصاص داشت. به کمک مثالی که بیان شد، روال و گام‌های مربوط به تحلیل را طی کرده و خروجی‌های حاصل را هم معرفی و تفسیر کردیم. به یاد داشته باشید که اگر در یک طرح آزمایش، امکان استفاده از اندازه مکرر وجود داشته باشد، بهره‌گیری از آن نسبت به روش آنالیز واریانس یک طرفه ساده، ارجح است. از آنجایی که SPSS گزینه‌های متعددی برای محاسبات پیچیده در این زمینه دارد، یکی از ابزار‌های محبوب برای تحلیل واریانس در بین کاربران محسوب می‌شود. همچنین، شرط‌ها و پیش‌فرض‌های اصلی برای اجرای آزمون تحلیل واریانس اندازه مکرر نیز در این متن مورد اشاره قرار گرفتند و روش‌های سنجش صحت آن ها نیز مورد بحث واقع شدند.