آزمون مقایسه زوجی در SPSS | راهنمای کاربردی

«آزمون‌های فرض آماری» (Hypothesis Testing)، یک روش برای بررسی صحت گزاره‌ای در مورد جامعه یا پارامتر جامعه آماری هستند. در این بین به علت خواص مطلوب میانگین برای توصیف رفتار جامعه، آزمون‌های مربوط به میانگین، از اهمیت ویژه‌ای برخوردار هستند. در این نوشتار به آزمون مقایسه زوجی در SPSS می‌پردازیم تا پس از آگاهی از نحوه اجرای آن، قادر به تفسیر خروجی‌های حاصل باشیم.

برای آشنایی بیشتر با نحوه کار در محیط SPSS و همچنین اجرای آزمون‌های آماری بهتر است مطالب پنجره ویرایشگر داده (Data Editor) در SPSS — راهنمای کاربردی و استنباط و آزمون فرض آماری — مفاهیم و اصطلاحات را مطالعه کنید. همچنین خواندن نوشتارهای آزمون فرض میانگین جامعه در آمار — به زبان ساده و آزمون تی (T Test) در R — راهنمای کاربردی نیز خالی از لطف نیست.

آزمون مقایسه زوجی در SPSS

در بسیاری از مواقع لازم است وضعیت اثر یک عامل روی میانگین جامعه مورد بررسی قرار گیرد. به این منظور طرح آزمایشی در نظر گرفته شده که طی آن، هر مشخصه یا ویژگی هر آزمودنی، قبل و بعد از تیمار صورت گرفته اندازه‌گیری می‌شود. تغییر در میانگین ویژگی، نشانه از اثر بخشی تیمار روی ویژگی مورد بحث دارد.

چنین آزمون را که از هر آزمودنی دو اندازه‌گیری صورت گرفته و مقادیر به صورت زوج مرتب (قبل از تیمار و بعد از تیمار) هستند، «آزمون مقایسه زوجی» (Paired Sample Test) می‌نامند. از آنجایی که با فرض وجود توزیع نرمال برای جامعه آماری، توزیع آماری مربوط به آماره آزمون در این حالت، دارای «توزیع تی» (t- Distribution) است، این آزمون به «نمونه‌های زوجی تی» (Paired sample t-Test) معروف است. آزمون مقایسه زوجی حتی زمانی که بخواهیم شباهت میانگین دو جامعه را مورد بررسی قرار دهیم نیز به کار گرفته می‌شود. البته به شرطی که هردو جامعه از بقیه جهات کاملا شبیه به یکدیگر باشند.

برای مشخص شدن موضوع و آشنایی با روال اجرای آزمون مقایسه زوجی در SPSS به صورت پارامتری، در ادامه یک مثال کاربردی را مطرح می‌کنیم.

مثال کاربردی از آزمون مقایسه زوجی در SPSS

یک آموزگار، سه امتحان برای یک درس ایجاد کرده است. او می‌خواهد میزان سختی یا سادگی سوالات این امتحانات را مورد بررسی قرار دهد. معلم از دانش آموزان می‌خواهد که به ترتیب تصادفی، در این سه امتحان شرکت کنند. متاسفانه از بین دانش آموزان کلاس فقط ۱۹ نفر داوطلب شدند، پس آموزگار به همه جامعه آماری (کل دانش آموزان کلاس‌هایش) دسترسی ندارد.

نمره یا تعداد پاسخ‌های صحیح دانش آموزان ملاک اندازه‌گیری سختی یا سادگی امتحان در نظر گرفته می‌شود. انتظار داریم اگر درجه سختی امتحانات یکسان باشند، دانش آموزان در هر نوع مقایسه دوتایی از این امتحانات، نمرات یکسانی گرفته باشند.

متاسفانه با توجه به نمونه ۱۹ نفری، به اطلاعات کل جامعه آماری دسترسی نداریم و مجبور به اجرای آزمون آماری هستیم. بنابراین حتی اگر در جامعه آماری، میانگین نمرات، یکسان باشد، ممکن است اختلاف در میانگین نمونه‌ها وجود داشته باشد. به کمک آزمون فرض آماری نشان می‌دهیم که اختلاف بین میانگین نمونه‌ها، ناشی از نمونه‌گیری است (و معنی‌دار نیست) یا واقعا نشانه اختلاف در جامعه است و در نتیجه اختلاف مشاهده شده در میانگین نمونه‌ها معنی‌دار و ناشی از تفاوت جامعه‌ها است.

به این ترتیب، آزمون فرض اول را با توجه به مقایسه امتحان اول و دوم، به صورت زیر می‌نویسیم.

$$ \large \begin{cases} H_0: & \text{mean} (ex1) = \text{mean} (ex2) \\ H_1: & \text{mean} (ex1) \neq \text{mean} (ex2) \end{cases} $$

و همچنین بررسی آزمون فرض امتحان اول و سوم نیز به شکل زیر خواهد بود.

$$ \large \begin{cases} H_0: & \text{mean} (ex1) = \text{mean} (ex3) \\ H_1: & \text{mean} (ex1) \neq \text{mean} (ex3) \end{cases} $$

و در انتها نیز مقایسه بین امتحان دوم و سوم صورت می‌گیرد.

$$ \large \begin{cases} H_0: & \text{mean} (ex2) = \text{mean} (ex3) \\ H_1: & \text{mean} (ex2) \neq \text{mean} (ex3) \end{cases} $$

نکته: به طور کلی می‌توانیم آزمون زوجی را به شکل سوالی در نظر بگیریم که در آن پرسیده می‌شود آیا هر دو متغیر دارای میانگین یکسان هستند یا خیر؟ همچنین با توجه به یکسان بودن تعداد مشاهدات در هر دو گروه یا متغیر، این آزمون را می‌توان به صورت مقایسه میانگین تفاضل دو متغیر نیز در نظر گرفت. این امر در انتهای این متن مورد بررسی قرار خواهد گرفت.

به این منظور از آزمون مقایسه زوجی (Paired Sample Test) استفاده خواهیم کرد. با توجه به بزرگ نبودن حجم نمونه باید توزیع جامعه را مورد بررسی قرار داده تا با توزیع نرمال مطابقت داشته باشد. در صورت صحت این امر، از آماره تی برای انجام آزمون کمک بگیریم.

برای دسترسی به مجموعه داده‌های compare-exams.sav مربوط به این مثال، فایل فشرده را از اینجا دریافت کنید و پس از خارج کردن از حالت فشرده، در SPSS بارگذاری نمایید.

متغیرهای تعریف شده در این آزمون را در تصویر ۱، مشاهده می‌کنید.

فرضیات اولیه برای اجرای آزمون مقایسه زوجی تی

با توضیحاتی که در قسمت قبل داده شده، می‌توانیم آزمون مقایسه زوجی را به صورت یک «آزمون تک نمونه‌ای» (One Sample t Test) نیز در نظر بگیریم. در این حالت، تفاضل مقادیر هر دو متغیر را ملاک قرار داده، یک آزمون تک نمونه‌ای اجرا می‌کنیم. ولی در این بین باید برای هر دو حالت، فرضیاتی را هم به همین جهت لحاظ کنیم.

• مشاهدات مستقل از یکدیگر باشند. به این معنی که نمره نفر $$i$$ام با نمره نفر بعدی ارتباطی نداشته باشد. از آنجایی که مشاهدات به صورت سطری در SPSS ثبت شده‌اند، این شرط لحاظ شده است.
• جامعه آماری برای زوج متغیرهای مورد آزمون (یا تفاضل آن‌ها)، باید«توزیع نرمال» (Normal Distribution) باشد. معمولا در زمانی که تعداد مشاهدات بیشتر از ۲۵ یا ۳۰ باشند، می‌توان با در نظر گرفتن کوچکی «چولگی نمونه‌ای» (Skewness)، توزیع جامعه را نرمال فرض کرد. ولی اگر تعداد نمونه کم باشد، نرمال بودن باید توسط روش‌های تصویری (رسم نمودار) یا آزمون‌های آماری (تست‌های نرمالیتی) مورد بررسی قرار گیرد.

در تصویر ۲، مقادیر مربوط به مجموعه داده compare exams.sav را مشاهده می‌کنید. واضح است که هر سطر از داده‌ها، نشانگر نمرات امتحان و ویژگی‌های یک دانش آموز است. در نتیجه مشاهدات از یکدیگر مستقل هستند.

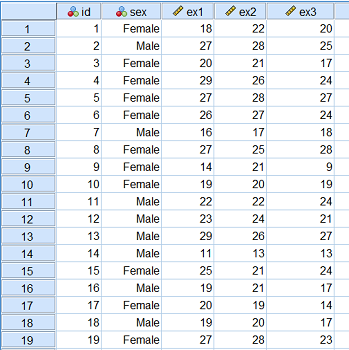
برای نرمال بودن این مجموعه داده نیز باید از «آزمون‌های ناپارامتری» (Non-parametric Test) متناسب، مثل «آزمون کولموگروف-اسمیرنف» (Kolmogorov-Smirnov) یا «آزمون شاپیرو-ولیک» (Shapiro-Wilk’s Test) استفاده کنیم. البته رسم «نمودار فراوانی» (Histogram) می‌تواند، کمک شایانی از شناخت وضعیت نرمال بودن داده‌ها در اختیارمان قرار دهد. ناگفته نماند این کار در قسمت‌های بعدی این متن و به کمک آزمون‌ها، مورد بررسی قرار گرفته است.

اجرای آزمون مقایسه زوجی در SPSS

اگر می‌خواهید آزمون مقایسه زوجی در SPSS را براساس «آماره تی» (T- Statistics) انجام دهید، باید از مسیر زیر اقدام کنید.

Analyze -> Compare Means -> Paired Samples T Test

البته در تصویر ۳، نیز محل قرارگیری دستور Paired-Sample T Test نمایش داده شده است.

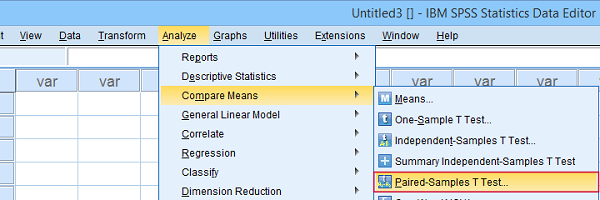
پس از اجرای دستور فوق، پنجره‌ای به نام Paired-Sample T Test، برای دریافت پارامترهای آن ظاهر می‌شود. کافی است دو متغیر را از کادر سمت چپ به طور همزمان انتخاب کرده و به کمک دکمه → به کادر Paired Variables بکشید. این کار در تصویر ۴، نمایش داده شده. واضح است که برای هر زوج متغیر (در کل سه روش ترکیب نمرات امتحانات) این کار باید تکرار شود.

نکته: برای انتخاب هر دو متغیر به طور همزمان، باید روی متغیر اول کلیک کرده و متغیره دوم را به کمک نگه داشتن کلید Ctrl و کلیک کردن، انتخاب کنید. به این ترتیب روی هر دو متغیر، نوار زرد رنگی ظاهر شده که به معنی انتخاب همزمان ‌آن‌ها است. کلید ↔ در این پنجره نیز ترتیب قرارگیری متغیرها را در زوج مرتب، تغییر می‌دهد. همچنین برای اولویت بندی در آزمون برای هر یک از زوج‌ها، از کلیدهای ↓ یا ↑ در این پنجره استفاده کنید.

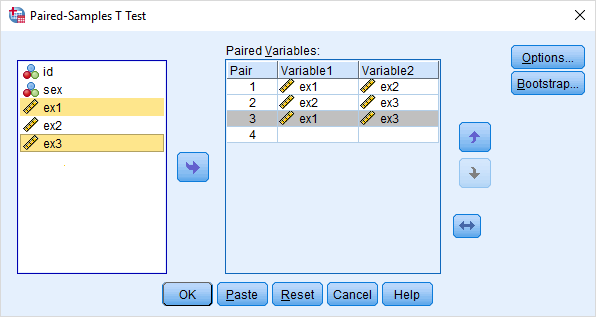
نکته: اگر بخواهید این فرمان و پارامترهایش را در محیط کدنویسی SPSS وارد و اجرا کنید، کافی است در پنجره Syntax، دستورات زیر را بنویسید. دکمه Paste در پنجره مربوط به تصویر ۴، همین کدها را ایجاد خواهد کرد. البته در کادر زیر، این دستورات به دو شکل نوشته شده که روش دوم خلاصه‌تر (Shorter) و با کدهای کمتر نمایش داده شده است.

*Syntax pasted from analyze - compare means - paired-samples t-test.

T-TEST PAIRS=ex1 ex1 ex2 WITH ex2 ex3 ex3 (PAIRED)
/CRITERIA=CI(.9500)
/MISSING=ANALYSIS.


*Shorter version below results in exact same output.

T-TEST PAIRS=ex1 to ex3
/CRITERIA=CI(.9500)
/MISSING=ANALYSIS.

خروجی این دستورات معمولا شامل چند شاخص آمار توصیفی، جدول ضریب همبستگی و جدول آزمون و فاصله اطمینان ۹۵٪ است. اگر می‌خواهید میزان اطمینان را تغییر دهید، از دکمه Options در پنجره پارامترها استفاده کنید و مقدار مورد نظرتان را در کادر Confidence Interval Percentage وارد کنید. در تصویر ۵، تنظیمات اختیاری (Options) را برای این دستور مشاهده می‌کنید. معمولا مقدار سطح اطمینان ۹۵٪ در نظر گرفته می‌شود.

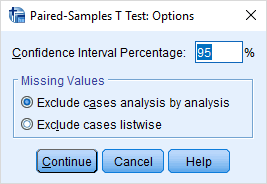
تفسیر خروجی‌های آزمون زوجی در SPSS

از آنجایی که سه زوج از متغیرها را برای آزمون انتخاب کرده‌ایم، SPSS‌ نیز سه خروجی نمایش خواهد داد. هر کدام از این زوج‌ها با نام‌های Pair1 تا Pair3 مشخص می‌شوند. ابتدا به اولین بخش از خروجی به نام جدول «شاخص‌های آماری زوجی» (Paired Samples Statistics) می‌پردازیم.

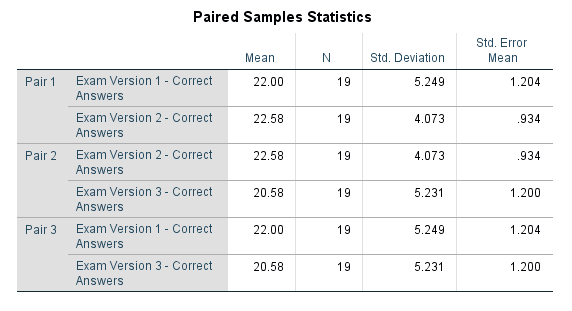
همانطور که در تصویر 6، قابل مشاهده است، «میانگین هر یک از متغیرها» (Mean)، «تعداد مشاهدات» (N)، «انحراف استاندارد» (Std.Deviation) و «خطای استاندارد میانگین» (Std. Error Mean) در این جدول دیده می‌شود. به نظر می‌رسد که میانگین‌ها برای زوج متغیرها، به یکدیگر نزدیک هستند. از طرفی واریانس یا انحراف معیار نیز برای متغیرها با هم اختلاف چندانی ندارد.

در قسمت بعدی خروجی SPSS، ضریب همبستگی بین زوج متغیرها محاسبه شده است تا نشانگر وجود رابطه بین آن‌ها باشد. اگر ضریب همبستگی بین آن‌ها ضعیف باشد، نشانه عدم اثر تیمار روی متغیر یا ویژگی مورد نظر است. در جدول مربوط به تصویر 7، «ضریب همبستگی پیرسون» (Pearson Correlation Coefficient) برای زوج متغیرها محاسبه شده است. بزرگ بودن ضریب همبستگی و همچنین معنی‌دار بودن مقادیر آن‌ها، با توجه به نزدیک صفر بودن مقدار .Sig، رای به وجود وابستگی بین زوج متغیرها می‌دهد. پس، ارتباطی که بین مقدارها برای دو متغیر حدس می‌زدیم، واقعا وجود دارد.

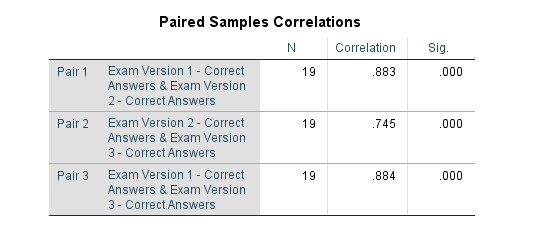
نکته: فرض بر این است که هر نفر در هر سه امتحان شرکت کرده است. پس نمره‌ای که در امتحان‌ها می‌گیرد وابسته به دانش او است. در نتیجه تنها عاملی که باعث اختلاف نمرات خواهد شد، تغییر سطح سختی یا سادگی سوالات هر سری امتحان است. واضح است که برای نمایش ارتباط نمرات با سطح دانش، ضریب همبستگی را محاسبه کرده و مورد بررسی قرار داده‌ایم.

در انتهای خروجی نیز نتیجه انجام آزمون مقایسه زوجی در SPSS را مشاهده می‌کنید. برای هر زوج از متغیرها مورد استفاده، یک سطر در نظر گرفته شده که اقلام مهم اطلاعاتی را نمایش می‌دهد. در فهرست زیر به بعضی از آن‌ها اشاره کرده‌ایم.

1. میانگین اختلاف دو متغیر (Mean) که انتظار داریم به صفر نزدیک باشد.
2. انحراف استاندارد اختلاف بین زوج‌ها.
3. فاصله اطمینان 95٪ برای اختلاف بین زوج‌ها. چنانچه این فاصله اطمینان شامل صفر باشد، دلیلی بر رد فرض صفر وجود نخواهد داشت.
4. در جدول زیر، مقدار Sig یا مقدار احتمال (p-Value) برای آزمون نیز دیده می‌شود. در صورتی که مقدار .Sig کمتر از احتمال خطای نوع اول (مثلا $$\alpha = 0.05$$) باشد، فرض صفر را رد خواهیم کرد.

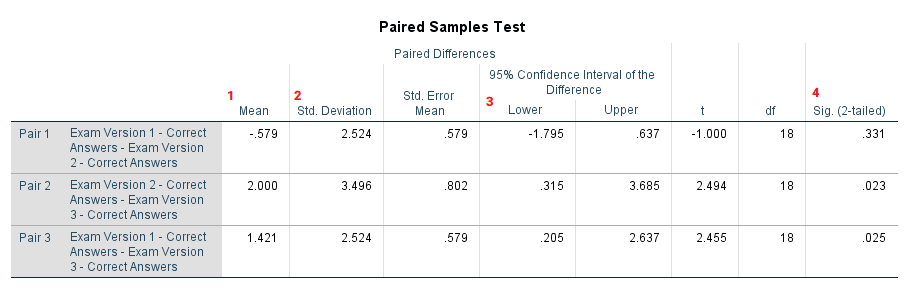
با توجه به خروجی ظاهر شده در تصویر 8، به نظر می‌رسد که امتحان سوم از امتحان اول و دوم ساده‌تر بوده زیرا میانگین اختلاف نمرات در این حالت مثبت شده. به این ترتیب مشخص می‌شود که امتحان اول و دوم از لحاظ سختی با یکدیگر معادل بوده ولی امتحان سوم نسبت به آن‌ها ساده‌تر است.

نکته: توجه داشته باشید که در اینجا آزمون‌ها به صورت جداگانه در نظر گرفته شده‌اند و نمی‌توان آن‌ها را به صورت یک آزمون هم‌زمان یا خطای توام در نظر گرفت در این صورت ممکن است خطای آزمون‌های هم‌زمان نسبت به آزمون‌ها تکی، افزایش زیادی داشته باشد، برای حل این مشکل معمولا از روش «اصلاح بونفرونی» (Bonferroni Correction) یا تحلیل «واریانس یک طرفه» (ANOVA) استفاده می‌شود.

آزمون نرمال بودن داده‌ها

در قسمت فرضیات آزمون مقایسه زوجی، به این موضوع اشاره کردیم که باید توزیع جامعه آماری نرمال باشد تا براساس آن از آماره t‌، استفاده کنیم. در این قسمت می‌خواهیم به کمک دو آماره «کولموگروف-اسمیرنف» و «شاپیرو-ویلک»، نرمال بودن اختلاف نمرات ترکیبات دو تایی از نتایج امتحانات را بسنجیم. ابتدا اختلاف زوج‌های نمرات امتحانی محاسبه و در متغیرهای متناظر به صورت dif_1_2 برای تفاضل امتحان اول و دوم یا dif_1_3 برای تفاضل نمرات امتحان اول و سوم یا dif_2_3 برای تفاضل نمرات امتحان دوم و سوم، ثبت می‌کنیم.

کد دستوری برای انجام این محاسبات نیز در زیر دیده می‌شود. البته می‌توانیم این عملیات را به کمک دستور Variable Compute از فهرست Transform نیز اجرا کنیم.

*Compute difference scores as new variables.

compute dif_1_2 = ex1 - ex2.
compute dif_1_3 = ex1 - ex3.
compute dif_2_3 = ex2 - ex3.
execute.

حال به بررسی آزمون نرمال بودن این اختلاف‌ها خواهیم پرداخت. از آنجایی که در نوشتارهای دیگر فرادرس به معرفی نحوه اجرای این آزمون‌ها پرداخته‌ایم، در اینجا فقط از قطعه کد زیر استفاده می‌کنیم تا نتایج مربوط به آزمون ظاهر شوند.

*Run normality tests from Analyze - Descriptive Statistics - Explore.
 
EXAMINE VARIABLES=dif_1_2 dif_1_3 dif_2_3
  /PLOT NPPLOT
  /STATISTICS NONE
  /CINTERVAL 95
  /MISSING LISTWISE
  /NOTOTAL.

*Note: difference score between 1 and 2 violates normality assumption.

مترادف این دستورات، استفاده از فهرست Analysis و گزینه Descriptive Statistics‌ و اجرای فرمان Explore است. پارامتر (PLOT NPPLOT\) نشانگر بررسی نرمال بودن متغیرها است. خروجی مطابق با تصویر ۹، خواهد بود.

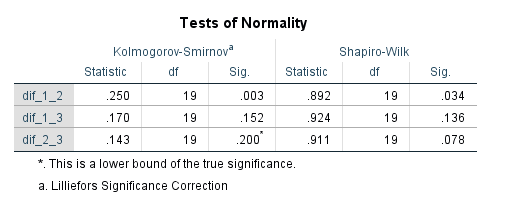
مقدار احتمال برای هر دو روش در جدول Tests of Normality دیده می‌شود. در سمت چپ، آماره و مقدار احتمال برای روش «کولموگروف-اسمیرنف» (Kolmogorov-Smirnov) قرار گرفته و در سمت راست نیز مقادیر مربوط به آزمون «شاپیرو-ولیک» (Shapiro-Wilk) دیده می‌شود.

در اینجا فرض صفر، نرمال بودن جامعه آماری برای هر یک از اختلافات است. اگر مقدار .Sig کوچکتر از احتمال «خطای نوع اول» ($$\alpha$$) باشد، فرض صفر را رد می‌کنیم. با توجه به خطای $$\alpha = 0.01$$، نرمال بودن  هیچ یک از جوامع، رد نمی‌شود، در نتیجه می‌توان به نتیجه آزمون مقایسه زوجی در این مثال اعتماد کرد. ولی اگر خطا را $$\alpha = 0.05$$ در نظر بگیریم، به نظر می‌رسد که اختلاف بین نمره امتحان اول و دوم، نرمال نبوده و برای انجام آزمون مقایسه‌ای بین میانگین آن دو بهتر است یا حجم نمونه را افزایش دهیم یا از آزمون‌های زوجی ناپارامتری مانند «آزمون ویلکاکسون» (Wilcoxon Signed Rank Test) استفاده کنیم.

آزمون تک نمونه‌ای برای مقایسه زوجی

همانطور که گفته شد، اگر اختلاف مقادیر زوج‌ها را مبنا قرار دهیم، آزمون مقایسه زوجی را می‌توان به صورت آزمون مقایسه میانگین با مقدار صفر در نظر گرفت. به این منظور کافی است از کد زیر استفاده کرده و نتایج را با خروجی‌های حاصل از روش قبلی مقایسه کنیم.

*Test if all difference scores have zero means.

T-TEST
/TESTVAL=0
/MISSING=ANALYSIS
/VARIABLES=dif_1_2 dif_1_3 dif_2_3
/CRITERIA=CI(.95).

نتیجه اجرای این دستورات در SPSS به صورت تصویر ۱۰، خواهد بود. در جدول اولی (One-Sample Statistics)، شاخص‌های آماری مانند میانگین و انحراف معیار نمایش داده شده. در جدول دوم (One-Sample Test) نیز آزمون تک نمونه‌ای اجرا شده و با توجه به مقدار (Sig. (2 tailed نتیجه می‌گیریم که فقط برای اختلاف امتحان اول و دوم، فاصله معنی‌دار نیست. در بقیه موارد و به شکل مستقل، نوع امتحان در نمره حاصل تاثیرگذار است. همچنین فاصله اطمینان ۹۵٪ نیز برای سطر اول شامل مقدار صفر شده ولی در دو سطر بعدی، شامل صفر نخواهد بود. این موضوع نیز نتایج حاصل از آزمون آماری را تایید می‌کند.

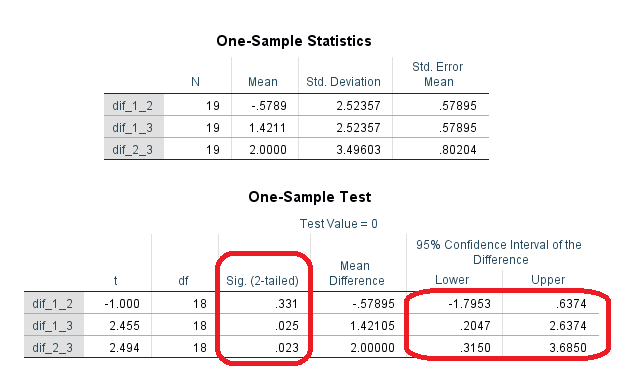
با توجه به کادرهای قرمز رنگی که در این تصویر مشاهده می‌شود، نتیجه می‌گیریم که اختلاف بین امتحان اول و دوم معنی‌دار نبوده ولی امتحان سوم با امتحان اول و دوم، اختلاف معنی‌داری دارد و فرض صفر بودن اختلاف در این حالت‌ها، رد می‌شود. البته این نتیجه‌ای بود که در قسمت قبلی به کمک آزمون مقایسه‌ای زوجی نیز بدست آوردیم. باز هم تاکید می‌کنیم که این روش، استدلال هم‌زمان برای مقایسه میانگین‌ها را بررسی نمی‌کند.

خلاصه و جمع‌بندی

با توجه به اهمیت مشخص کردن اثر تیمارها روی مشاهدات یکسان، آزمون مقایسه زوجی در SPSS موضوع این مطلب قرار گرفت. به این ترتیب دیدیم که چگونه چنین آزمونی‌هایی را می‌توان با توجه به شرایط اجرای آن در SPSS‌ انجام داد. البته به کمک مثالی که به مقایسه سه نوع امتحان و فرض برابری نمرات در آن‌ها می‌پرداخت، نحوه کار را معرفی کردیم. در ضمن فرضیات اولیه اجرای آزمون مقایسه زوجی را هم در مورد بررسی قرار داده و شیوه صحت این فرضیات را هم بیان کردیم. در انتها نیز نتایج حاصل از آزمون آماری را به همراه تفسیر آن‌ها، ارائه شد.