انحراف استاندارد و خطای استاندارد — از صفر تا صد

اغلب در محاسبات و آزمون‌های آماری با دو واژه شبیه به هم به نام‌های انحراف استاندارد و خطای استاندارد مواجه می‌شویم. از آنجایی که این دو عبارت هر دو کلمه استاندارد را یدک می‌کشند، به نظر می‌رسند که یک ملاک عمومی برای سنجش ویژگی‌هایی آماری باشند. ولی آیا انحراف استاندارد و خطای استاندارد با یکدیگر تفاوت دارند یا واژه‌ای برای بیان یک خاصیت از جامعه آماری هستند؟ در این نوشتار می‌خواهیم به تفاوت و البته ارتباطی که بین این دو اصطلاح آماری وجود دارند، بپردازیم.

به این منظور بهتر است ابتدا نوشتارهای دیگر مجله فرادرس مانند واریانس و اندازه‌های پراکندگی — به زبان ساده و امید ریاضی (Mathematical Expectation) — مفاهیم و کاربردها را مطالعه کنید. همچنین خواندن مطالب متغیر تصادفی، تابع احتمال و تابع توزیع احتمال، آزمایش تصادفی، پیشامد و تابع احتمال و میانگین وزنی — به زبان ساده نیز خالی از لطف نیست.

انحراف استاندارد و خطای استاندارد

در مباحث آماری، داده‌های جمع‌آوری شده، اغلب با استفاده از مقدار «میانگین» (Mean) و «انحراف استاندارد نمونه‌ای» (Sample Standard Deviation) توصیف می‌شوند. همچنین ممکن است این کار بوسیله مشخص کردن مقدار میانگین و «خطای استاندارد» (Standard Error) صورت گیرد.

با توجه به نزدیک بودن معنی دو اصطلاح انحراف استاندارد و خطای استاندارد اغلب ممکن است با یکدیگر اشتباه گرفته شده یا به شکل یکسانی تفسیر شوند. به یاد داشته باشید که میانگین و انحراف استاندارد، شاخص‌های توصیفی برای جامعه یا نمونه آماری هستند، در حالی که خطای استاندارد یا به طور دقیق‌تر، «خطای استاندارد میانگین» (Standard Error of Mean)، شاخصی برای سنجش خطای برآوردگر و توصیفی از روش نمونه‌گیری تصادفی است.

انحراف استاندارد از داده‌های حاصل از جامعه یا نمونه آماری تولید می‌شود. در مقابل، خطای استاندارد میانگین، یک عبارت احتمالی در مورد نسبت اندازه نمونه و انحراف استاندارد نمونه‌ای است. این شاخص، با توجه به «قضیه حد مرکزی» (Central Limit Theorem)، سعی در اندازه‌گیری خطای برآورد میانگین جامعه آماری دارد.

به عبارت ساده، خطای استاندارد میانگین نمونه، تخمین می‌زند که میانگین نمونه از میانگین جمعیت تا چه حد دور یا نزدیک است. در مقابل انحراف استاندارد شاخصی است که متوسط اختلاف مقادیر از میانگین نمونه یا جامعه آماری را نشان می‌دهد.

اگر انحراف استاندارد جمعیت متناهی باشد، خطای استاندارد میانگین نمونه با افزایش حجم نمونه به صفر می‌رسد، زیرا برآورد میانگین جمعیت بهبود می‌یابد، در حالی که انحراف استاندارد (نمونه یا جامعه) اغلب با اضافه شدن مشاهده جدید به داده‌ها، افزایش می‌یابد.

به این ترتیب مشخص است که باید بین انحراف استاندارد و خطای استاندارد تفاوت قائل شد. در ادامه توضیحات بیشتری نیز ارائه می‌شود.

انحراف استاندارد یک شاخص توصیفی

همانطور که گفته شد، انحراف استاندارد ابزاری برای نمایش میزان پراکندگی داده‌ها است. شیوه محاسبه «انحراف استاندارد» درست شبیه «واریانس» (Variance) است. به فرمول زیر توجه کنید. در نظر بگیرید که جامعه‌ای شامل $$N$$ مقدار مختلف مانند $$x_1, x_2 , \ldots, x_N$$ داریم و می‌خواهیم واریانس و انحراف استاندارد را محاسبه کنیم.

$$  \large \text{Var}(x) = \frac{1}{N} \sum_{i = 1}^N (x_i – \overline{x} )^2 $$

که در آن $$\bar{x}$$، میانگین مقادیر $$X$$ است. براساس واریانس، انحراف استاندارد بدست می‌آید.

$$  \large \text{sd}(x) = \sqrt{\text{Var}(x)} $$

البته شایان ذکر است که اگر به جای جامعه آماری، مشاهدات حاصل از یک نمونه‌ای آماری از جامعه بودند، محاسبه واریانس و انحراف استاندارد کمی با تغییر همراه بود. نحوه محاسبه واریانس نمونه‌ای و انحراف استاندارد نمونه‌ای در ادامه دیده می‌شود.

در اینجا فرض بر این است که یک نمونه $$n$$ تایی از جامعه آماری به صورت $$X_1,X_2 ,\ldots,X_n$$ در اختیارمان قرار گرفته است.

نکته: توجه داشته باشید که در فرمول مربوط به واریانس یا انحراف معیار جامعه از $$x$$ استفاده کردیم، زیرا متغیر تصادفی نیستند. ولی برای محاسبه واریانس و انحراف معیار نمونه‌ای از نماد $$X$$ استفاده می‌شود تا نشان دهنده تصادفی بوده آن‌ها باشد، زیرا مقدار آن‌ها از نمونه‌ای به نمونه دیگر متفاوت است.

$$  \large \text{Var}(X) = \frac{1}{n-1} \sum_{i = 1}^n (X_i – \overline{X} )^2 $$

و همچنین برای انحراف معیار نمونه‌ای نیز همان ارتباط با واریانس را خواهیم داشت.

$$  \large \text{sd}(X) = \sqrt{\text{Var}(X)} $$

نکته: در مخرج محاسبه واریانس نمونه‌ای از $$n-1$$ استفاده شده تا یک «برآوردگر نااریب» (Unbiased Estimator) حاصل شود.

موضوع مهم در محاسبه واریانس و انحراف معیار، استفاده از میانگین به عنوان یک نقطه مرکزی و سنجش مجموع مربعات فاصله‌های مقادیر دیگر نسبت به آن است. در این حالت فقط از معیار مرکزی برای انجام محاسبات استفاده شده ولی برای برآورد آن، این عمل صورت نگرفته است و مستقیما براساس انحراف استاندارد بدست می‌آید.

خطای استاندارد میانگین

نمونه‌گیری از جامعه آماری با هدف برآورد پارامترها و شناخت آن جامعه صورت می‌پذیرد. به این ترتیب میانگین حاصل از یک نمونه تصادفی به اسم $$\overline{X}$$ می‌تواند برآورد مناسبی برای میانگین جامعه آماری باشد. ولی از آنجایی که مقدار این برآورد از نمونه‌ای به نمونه دیگر متفاوت است، آن را یک «متغیر تصادفی» (Random Variable) یا  «آماره» (Statistics) می‌نامیم.

پس مشخص است که برآورد میانگین که توسط یک نمونه تصادفی حاصل شده، دارای خطا است. این خطا توسط «خطای استاندارد میانگین» (Standard Error) اندازه گیری می‌شود.

بنابراین باید مشخص کنیم که اگر $$\mu$$ میانگین واقعی برای جامعه آماری باشد، برآورد آن یعنی $$\overline{X}$$ چقدر از آن فاصله دارد. این فاصله را می‌توان به وسیله واریانس معرفی و محاسبه کرد.

البته می‌دانیم که انتظار داریم میانگین برآوردگرها ($$\bar{\overline{X}}$$) به میانگین واقعی نزدیک و تقریبا با آن فاصله‌ای نداشته باشد. این ویژگی را برای یک برآوردگر، «نااریبی» (Unbiasness) می‌نامند. پس به این ترتیب داریم:

$$ \large \mu = E(\overline{X}) $$

که در آن $$E$$، نماد یا عملگر «امید ریاضی» (Mathematical Expectation) یا «مقدار مورد انتظار» (Expected Value) یا چشم داشتی است. حال فاصله برآوردگر از پارامتر یا مقدار مورد انتظار را برحسب واریانس محاسبه می‌کنیم. طبق تعریف واریانس مجموع متغیرهای تصادفی مستقل داریم:

$$\large \text{Var}(\overline{X_i}) = \text{Var}\frac{1}{n}\sum_{i = 1}^n ({X_i}) = \frac{1}{n^2}\sum_{i=1}^n \text{Var}(X_i) = \dfrac{n\sigma^2}{n^2}=\frac{\sigma^2}{n} $$

از طرفی انحراف معیار براساس این واریانس نیز به صورت زیر حاصل می‌شود.

$$ \large SE(\overline{X}) = {\sqrt {\text{Var}}(\overline{X})} = \frac{\sigma}{\sqrt{n}} $$

رابطه محاسبه خطای استاندارد میانگین برحسب انحراف معیار

توجه داشته باشید که اگر انحراف معیار جامعه ($$\sigma$$) مشخص نباشد، باید از برآوردگر انحراف معیار نمونه‌ای استفاده کرد. البته این کار احتیاج به یک ضریب تصحیح نیز دارد که در ادامه این مطلب به آن اشاره خواهیم کرد.

 نکته: همانطور که مشاهده می‌شود، با افزایش تعداد نمونه‌ها، واریانس خطای میانگین و در نتیجه خطای استاندار میانگین، کاهش می‌یابد. زیرا اثر افزایش تعداد، دوبار تاثیر گذار است. یکبار در محاسبه واریانس یا انحراف استاندارد نمونه‌ای که مجموع مربعات به تعداد تقسیم می‌شود و یکبار هم هنگام محاسبه خطای استاندارد میانگین، عمل تقسیم صورت می‌گیرد.

انتخاب آزمون و اجرای روش‌های توصیفی در آمار احتیاج به مهارت و شناخت کامل از جنبه‌های آماری دارد. در آموزشی که لینک آن در ادامه آمده است، برای رشته‌های علوم انسانی، این مفاهیم به زبان ساده گفته و آموزش داده شده است.

• برای مشاهده فیلم آموزش آمار و کاربرد آن در علوم انسانی + اینجا کلیک کنید.

ضریب تصحیح جامعه متناهی و همبستگی نمونه‌ای

محاسبه خطای استاندارد میانگین به دلیل اهمیت آن در برآورد میانگین و اندازه خطای آن، باید با دقت صورت گیرد. در این میان دو دلیل برای به کار بردن ضریب تصحیح وجود دارد که اولی متناهی بودن جامعه آماری و دومی همبستگی بین نمونه‌های تصادفی است. ابتدا ضریب تصحیح جامعه متناهی را توضیح داده، سپس به بررسی همبستگی نمونه‌ها خواهیم پرداخت.

ضریب تصحیح برای محاسبه انحراف استاندارد و خطای استاندارد

معمولا هنگام محاسبه انحراف معیار و خطای استاندارد میانگین، فرض بر این است که اندازه جامعه ($$N$$) بسیار بزرگ بوده و در مقابل، حجم نمونه ($$n$$) کوچک است. ولی اگر حجم نمونه بزرگ باشد و بیش از ۵٪ جامعه آماری را شامل شود، بهتر است انحراف استاندارد و خطای استاندارد میانگین را به کمک یک ضریب تصحیح، بهینه کرد. این ضریب برای هر یک از این شاخص‌ها به صورت زیر نوشته می‌شود.

$$ \large {\displaystyle {\sqrt{\dfrac{N}{N – 1}} }} $$

ضریب تصحیح جامعه متناهی برای انحراف استاندارد

$$ \large {\displaystyle {\text{FPC}} = {\sqrt {\frac {N – n}{N – 1}}}} $$

ضریب تصحیح جامعه متناهی برای خطای استاندارد میانگین

مشخص است که برای انحراف استاندارد، ضریب تصحیح باعث ایجاد یک «برآوردگر نااریب» (Unbiased Estimator) می‌شود.

نکته: عبارت FPC مخفف «تصحیح جامعه متناهی» (Finite Population Correction) است.

برای جوامعی که اندازه جامعه بزرگ باشد، می‌توان ضریب تصحیح را به صورت زیر بدست آورد.

$$ \large {\displaystyle {\text{FPC}} \approx {\sqrt {1 – {\frac {n}{N}}}}} $$

البته در صورتی که نمونه‌های تصادفی، مستقل از یکدیگر نبوده و با هم به میزان ثابتی مثل $$\rho$$، وابستگی داشته باشند، ضریب تصحیح به صورت زیر نوشته خواهد شد.

$$ \large {\displaystyle f = {\sqrt {\frac {1 + \rho }{1 – \rho }}}} $$

توجه داشته باشید که وابستگی بین نمونه‌ها، بوسیله ضریب «همبستگی سریالی» یا «ضریب خود همبستگی» (Auto-correlation) مرتبه اول مورد محاسبه قرار می‌گیرد.

در ادامه برای درک بهتر مفهوم اصطلاحات انحراف استاندارد و خطای استاندارد به شکل ساده (بدون در نظر گرفتن ضریب تصحیح)، به ذکر مثال و محاسباتی در این رابطه می‌پردازیم.

محاسبه انحراف استاندارد و خطای استاندارد در زبان برنامه‌نویسی R

این بخش اختصاص به بررسی کدهایی دارد که به زبان برنامه‌نویسی R نوشته شده‌اند و به ما تفاوت بین انحراف معیار و خطای استاندارد را نشان می‌دهند. ابتدا یک سری داده تصادفی از توزیع نرمال (۱۰ مشاهده) تولید کرده و انحراف معیار آن‌ها را محاسبه می‌کنیم.

generating some random data
set.seed(20151204)
#computing the standard deviation
x <- rnorm(10)
sd(x)
# result: 1.144105

نتیجه محاسبات با توجه به مقدار seed، برابر است با 1.144105 که انحراف معیار نمونه‌ای است. در برنامه بعدی نمودار توزیع نرمال با میانگین صفر و واریانس یک را ترسیم کرده‌ایم.

نکته: استفاده از دانه تصادفی (Seed) باعث می‌شود که تولید داده‌های تصادفی در هر بار تکرار این برنامه، یکسان باشد. در نتیجه خروجی حاصل از این برنامه برای شما هم برابر با همین مقدار 1.144105 خواهد بود.

#generating the normally distributed graph with description of segments

plot(seq(-3.2,3.2,length = 50),dnorm(seq(-3,3,length = 50),0,1),type="l",xlab="",ylab="",ylim = c(0,0.5))
segments(x0 = c(-3,3),y0 = c(-1,-1),x1 = c(-3,3),y1 = c(1,1))

text(x = 0,y = 0.45,labels = expression(" 99.7% of the data within 3" ~ sigma))
arrows(x0 = c(-2,2),y0 = c(0.45,0.45),x1 = c(-3,3),y1 = c(0.45,0.45))
segments(x0 = c(-2,2),y0 = c(-1,-1),x1 = c(-2,2),y1 = c(0.4,0.4))
text(x = 0,y = 0.3,labels = expression("95% of the data within 2" ~ sigma))
arrows(x0 = c(-1.5,1.5),y0 = c(0.3,0.3),x1 = c(-2,2),y1 = c(0.3,0.3))
segments(x0 = c(-1,1),y0 = c(-1,-1),x1 = c(-1,1),y1 = c(0.25,0.25))
text(x = 0,y = 0.15,labels = expression("68% of the data within 1" * sigma),cex=0.9)

نتیجه اجرای کد بالا، تصویری است که در پایین دیده می‌شود. نقطه‌هایی با فاصله یک انحراف معیار از میانگین نیز مشخص شده‌اند که حدود ۶۸ درصد داده‌ها را تشکیل می‌دهد.

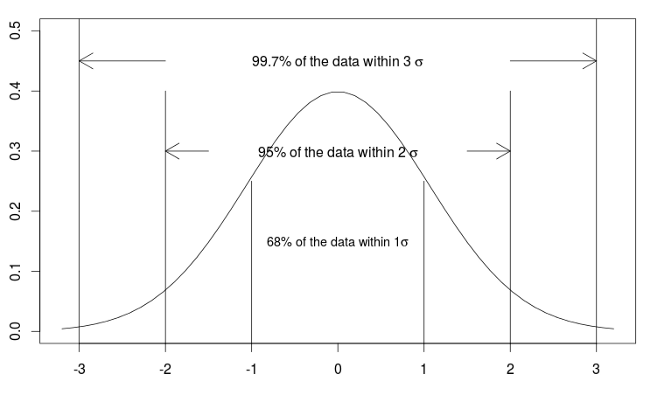
همچنین در فاصله ۲ انحراف استاندارد از میانگین، حدود ۹۵ درصد داده‌ها قرار گرفته‌اند. اگر سه انحراف استاندارد از میانگین دور شویم، تقریبا ۹۹.۷ درصد از داده‌ها را پوشش داده‌ایم. به این ترتیب مشخص است که انحراف معیار، شاخصی برای نمایش دوری یا نزدیکی به میانگین است.

حال این بار فرض کنید که عمل نمونه‌گیری از چنین جامعه‌ای را چندین بار تکرار کرده‌ایم و هر بار یک مقدار برای میانگین نمونه‌ای بدست آورده‌ایم. خطای استاندارد، واریانس یا انحراف معیار این مقادیر را نشان می‌دهد.

نکته: توجه داشته باشید که در اینجا به علت بدست آوردن نمونه‌های متنوع از اجرای دستور set.seed چشم‌پوشی کرده‌ایم. بنابراین ممکن است نتیجه محاسبه شما با چیزی که در این متن به آن اشاره شده، اندکی تفاوت داشته باشد.

# generating some random data
# set.seed(20151204)
#computing the standard Error of Mean
m = 1000
n = 10
xbar=rep(0,m)
for (i in 1: m)
{
x <- rnorm(n)
sdx = sd(x)
xbar[i] = mean(x)
}
sd(xbar)

sdx/sqrt(n)

طی برنامه بالا، فرض کرده‌ایم که از جامعه نرمال با میانگین صفر و واریانس ۱، هر بار ۱۰ (n = 10) نمونه تصادفی گرفته و میانگین و انحراف معیار آن نمونه را محاسبه کرده‌ایم. این کار را به تعداد هزار بار (m = 1000) تکرار کرده‌ایم و هزار میانگین نیز حاصل شده است. انحراف معیار میانگین‌های بدست آمده، همان خطای استاندارد میانگین هستند. شما می‌توانید با تغییر مقدار m یا n، نتایج دیگری بدست آوردید و به شکلی، تخمین میانگین جامعه را با افزایش تعداد تکرارها، بهتر انجام دهید.

به منظور تاکید بیشتر در انتها نیز، طبق رابطه انحراف استاندارد و خطای استاندارد میانگین، انحراف استاندارد نمونه‌ای را بر جذر تعداد مشاهدات تقسیم کرده‌ایم تا خطای استاندارد حاصل شود. همانطور که در ادامه مشاهده می‌کنید، این دو مقدار تقریبا برابر یکدیگرند. با افزایش تعداد تکرارها (m)، خطای استاندارد میانگین حاصل از نمونه‌های تصادفی و همچنین فرمول مربوطه به یکدیگر نزدیک خواهند شد.

> sd(xbar)
[1] 0.3136362
> 
> sdx/sqrt(n)
[1] 0.3330717
> 

در ادامه خطای استاندارد برای n=10000 در دو حالت محاسبه و نمایش داده شده است. واضح است که با افزایش تعداد نمونه‌ها، برآورد میانگین جامعه آماری بهتر صورت می‌گیرد.

> sd(xbar)
[1] 0.009518343
> 
> sdx/sqrt(n)
[1] 0.009943788

مقدار خطای استاندارد در اینجا نشان می‌دهد که با افزایش حجم نمونه، خطای برآورد میانگین کاهشی است و دقت در برآورد میانگین بهتر شده است.

نکته: معمولا برای نمایش دقت برآوردگر و نشان دادن رابطه آن با حجم نمونه، از خطای استاندارد میانگین استفاده می‌کنند. در اینجا هم دیدیم که این رابطه براساس حجم نمونه، نزولی است و هرگاه حجم نمونه افزایش یابد، خطای برآورد کاهش یافته و در مقابل، دقت برآورد افزایش خواهد یافت. از طرفی اگر انحراف استاندارد جامعه زیاد باشد، دقت برآورد یا خطای استاندارد نیز افزایشی خواهد بود و برآورد مناسب و با دقتی حاصل نخواهد شد، مگر آنکه حجم نمونه را افزایش دهیم.

معرفی فیلم آموزش آمار و کاربرد آن در علوم انسانی

آمار، علم شناخت محیط پیرامون و پدیده‌های تصادفی است. دسته بندی و خلاصه نمودن اطلاعات و این گونه داده‌ها به فهم و درک بیشتر نسبت به این پدیده‌ها کمک می‌کند. مدیران به عنوان برنامه‌ریزان و هدایت‌کنندگان سازمان‌ها و نهادها، باید به این ابزار مسلط بوده تا بتوانند جایگاه مناسبی برای سازمان خود ایجاد کرده و نقش هدایت‌گری را به بهترین نحو، اجرا کنند.

در این فرادرس که با عنوان آمار و کاربرد آن در علوم انسانی تدریس شده است، مطالب آمار توصیفی، و آمار استنباطی مورد بررسی قرار گرفته و با ذکر مثال‌هایی مفاهیم تدریس می‌شوند. فهرست سرفصل‌ها به طور خلاصه به شرحی هستند که در ادامه آمده‌اند.

از درس اول تا درس سوم، مربوط به تعریف آمار و محاسبه شاخص‌های آماری توصیفی است. درس چهار تا ششم و درس هفتم تا به درس یازدهم به متغیرهای تصادفی و همچنین توزیع نرمال می‌پردازد. این فیلم آموزشی برای دانشجویان رشته‌های مدیریت، حسابداری و اقتصاد مفید است. طول این دوره ویدیویی آموزشی ۵ ساعت و ۲۷ دقیقه در نظر گرفته شده است.

خلاصه و جمع‌بندی

در این نوشتار از مجله فرادرس، با دو مفهوم اساسی به نام‌های انحراف استاندارد و خطای استاندارد آشنا شدیم که به رغم شباهت‌هایشان، تفاوت‌های مهم و چشم‌گیری دارند. همانطور که دیدید، انحراف استاندارد یا معیار، به عنوان یک شاخص پراکندگی برای مقادیر دیده می‌شود، در حالیکه خطای استاندارد میانگین، مربوط به پراکندگی برآوردگر میانگین جامعه آماری از پارامتر واقعی آن است. به این ترتیب، واریانس و انحراف معیار به عنوان مقداری توصیفی و خطای استاندارد میانگین ابزاری برای استنباط آماری یا برآورد نقطه‌ای است.