فیزیک کوانتوم چیست؟ – از مفاهیم تا کاربردها به زبان ساده
هنگامی که به اطرافمان نگاه میکنیم با پدیدههای پیوسته و گسستهای روبرو میشویم. تعداد پلههایی که بالا یا پایین میرویم گسسته و انرژی مصرفی در طی روز پیوسته است. اما در دنیای اتمها و ذرات بنیادی با پدیدههای بسیار متفاوتتری روبرو میشویم. برای توضیح این پدیدهها از فیزیک کوانتوم استفاده میکنیم. همچنین این شاخه از فیزیک در مورد شکلگیری کهکشانها، ستارهها و تئوری Big Bang (مهبانگ یا انفجار بزرگ) توضیح میدهد. در این مطلب از مجله فرادرس ابتدا با فیزیک کوانتوم آشنا میشویم و سپس در مورد نظریه دوگانگی ذره یا موج، تابش جسم سیاه، عدمقطعیت هایزنبرگ، تابع موج شرودینگر، جهانهای موازی و کاربردهای فیزیک کوانتوم صحبت خواهیم کرد.
- میآموزید که فیزیک کوانتوم چیست و چه تفاوتی با فیزیک کلاسیک دارد.
- در مورد رفتار ذرهای و موجی اطلاعاتی به دست خواهید آورد.
- با مباحثی مانند چندجهانی و مشخصهیابی ستارهها آشنا میشوید.
- تبخیر سیاهچالهها و توضیح ساختار بزرگ جهان را فراخواهید گرفت.
- درهمتنیدگی کوانتومی و تابش جسم سیاه را بهطور کامل خواهید شناخت.
- یاد میگیرید معادله موج شرودینگر چیست و چه اهمیتی در فیزیک کوانتوم دارد.


فیزیک کوانتوم چیست؟
فیزیک کوانتوم در مورد فیزیک در ابعاد بسیار کوچک مطالعه میکند و به بررسی رفتار ماده و انرژی در مقیاس بسیار کوچکی مانند اتمها و ذرات زیراتمی میپردازد. در فیزیک کوانتوم انتقال انرژی به شکل کوانتومی و گسسته انجام میشود و ذرات میتوانند علاوهبر رفتار ذرهای، رفتار موجی نیز داشته باشند. همچنین در این شاخه از علم فیزیک با اصل عدمقطعیت آشنا میشویم که بر اساس آن نمیتوان مکان و سرعت یک ذره را همزمان با هم و بهطور دقیق تعیین کرد.
این شاخه از فیزیک در مورد سیستمهای بزرگمقیاسی (Macroscopic) مانند کهکشانها و ستارهها نیز توضیح میدهد. اما قبل از توضیح در مورد اصول فیزیک کوانتوم، سوالی که مطرح میشود آن است که چرا این شاخه از فیزیک به وجود آمد و تفاوت آن با فیزیک کلاسیک چیست؟ آیا معنای واژه کوانتوم را میدانید؟ در بخش بعد ابتدا به این پرسش پاسخ میدهیم. همچنین برای اینکه با روش یادگیری مفاهیم فیزیک بهتر آشنا شوید، پیشنهاد میکنیم پیش از شروع مطلب «بهترین روش مطالعه فیزیک چیست؟ – ۱۶ روش از مطالعه مفهومی تا حل مثال» را مطالعه کنید.
کوانتوم چیست؟
کوانتوم در زبان لاتین به معنای مقدار است. اما در علم فیزیک به کوچکترین واحد گسسته ممکنِ هر مشخصه فیزیکی، مانند ماده یا انرژی، کوانتوم گفته میشود. این واژه برای نخستین بار توسط «ماکس پلانک» (Max Planck) استفاده شد.
تفاوت فیزیک کلاسیک با فیزیک کوانتوم چیست؟
تفاوتهای اساسی زیادی بین فیزیک کلاسیک و فیزیک کوانتوم وجود دارند که در ادامه در مورد آنها صحبت میکنیم. در فیزیک کلاسیک، با داشتن دانش کامل در مورد گذشته، آینده را محاسبه خواهیم کرد. به طور مشابه، با داشتن علم کافی در مورد آینده، اطلاعات و محاسبات دقیقی از گذشته انجام میدهیم. اما در فیزیک کوانتوم شرایط متفاوت خواهد بود. ذرات در فیزیک کوانتوم به تنهایی نه ذره و نه موج هستند، بلکه ترکیبی از این دو خواهند بود. با داشتن دانش و علم کافی در مورد گذشته، در مورد آینده با قطعیت نمیتوانیم نظری بدهیم. تنها میتوانیم در مورد احتمال وقوع برخی اتفاقات صحبت کنیم.
در فیزیک کلاسیک دو بمب با فیوزهای یکسان در زمان یکسانی منفجر میشوند. اما در فیزیک کوانتوم دو اتم رادیواکتیو یکسان در زمانهای بسیاری متفاوتی منفجر خواهند شد. به عنوان مثال، زمانهای واپاشی رادیواکتیو دو اتم یکسان اورانیوم ۲۳۸ در حدود میلیونها سال با یکدیگر تفاوت دارند.
فیزیکدانها برای جدایی فیزیک کلاسیک از فیزیک کوانتوم از ثابت پلانک استفاده میکنند. اگر ثابت پلانک در معادلهای ظاهر شد، آن معادله مربوط به فیزیک کوانتوم است. در حالتهای حدی، فیزیک کلاسیک از فیزیک کوانتوم استخراج میشود که به آن اصل تطابق گفته میشود. به هنگام مطالعه فیزیک کوانتوم با پدیدههای عجیبی مواجه میشویم. بهطور مثال نور در مکانیک کوانتوم به صورت ذره و موج رفتار میکند. این رفتار دوگانه نور یکی از عجیبترین بخشهای فیزیک کوانتوم است.
چرا فیزیک کوانتوم عجیب است؟
به هنگام مطالعه فیزیک کلاسیک با پدیدههای فیزیکی روبرو میشویم که به مراتب در زندگی روزمره رخ دادهاند. اما در مکانیک کوانتوم اینگونه نیست. درک برخی پدیدهها بسیار سخت است. جهان کوانتوم اشتراک بسیار زیادی با کفشها دارد. هنگامی که برای خرید کتونی وارد مغازه کفشفروشی میشوید، هر کفشی با اندازه دلخواه را نمیتوانید انتخاب کنید. در واقع، داخل مغازه باید از بین اندازههای از قبل مشخص شده، کفش مورد نظر را انتخاب کنید. دنیای ریزاتمی مشابه همین حالت است.
آلبرت انیشتین به دلیل اثبات گسسته بودن انرژی برنده جایزه نوبل شد. همانگونه که کفشها اندازههای مشخصی دارند، مقادیر انرژی نیز گسسته و دارای مقدارهای مشخصی هستند. در حالت کلی، اندازه انرژی مضربی از کوانتاهای یکسانی است. در نتیجه، نام این شاخه از فیزیک، فیزیک کوانتوم است. کوانتا در اینجا ثابت پلانک و نام پلانک برگرفته از نام ماکس پلانک، پدر مکانیک کوانتوم، است. با فرض گسسته بودن انرژی، فرضیههای تئوری بسیاری با آزمایشهای انجام شده همخوانی پیدا کردند.

رفتار ذره ای یا موجی
«جی. جی. تامسون» (J. J. Thomson) در سال ۱۹۰۶ به دلیل کشف ذرهای بودن الکترونها برنده جایزه نوبل شد. درسال ۱۹۳۷، جرج پسر تامسون به دلیل آنکه نشان داد الکترونها موج هستند، برنده جایزه نوبل شد. اما کدام رفتار درست است؟ پاسخ، هر دو رفتار است. دوگانگی موج ذره بنیاد فیزیک کوانتوم است. این دوگانگی هم در مورد الکترونها و هم در مورد نور صادق است. گاهی اوقات برای توجیه برخی پدیدههای فیزیکی، رفتار موجی نور در نظر گرفته میشود. اما، گاهی در نظر گرفتن نور به عنوان ذراتی به نام فوتون مفید است.
تلسکوپ امواج نوری را که از ستارههای دور به آن میرسد، در یک نقطه جمع میکند. همچنین، به عنوان سطل نوری برای جمعآوری فوتونها رفتار خواهد کرد. این بدان معنا است که نور به هنگام برخورد با جسم، بر آن فشار وارد میکند. این فشار ناشی از برخورد فوتونهای تشکیلدهنده نور بر جسم است.
دوگانگی موج/ذره به خاصیت بنیادی ماده مربوط میشود که در یک لحظه مانند موج و در لحظهای دیگر مانند ذره رفتار میکند. به منظور داشتن درک بهتری از این دوگانگی، به تفاوت ذرات با امواج دقت کنید.
همه ما با ذراتی مانند مهرهها، شنهای ریز، اتمها و الکترونها آشنا هستیم. مشخصات ذرهها میتوانند با استفاده از مهرهها یا تیله ها توضیح داده شوند. تیله شکلی کروی دارد و در نقطهای از فضا قرار گرفته است. اگر با دست ضربهای به آن بزنیم، انرژی از دست ما به تیله منتقل خواهد شد. اگر تعداد زیادی تیله را بر روی زمین پخش کنیم، به یکدیگر برخورد خواهند کرد. در نتیجه این برخوردها، انرژی بین تیلهها منتقل میشود.

در مقابل، امواج مانند موج صوتی پخش میشوند. اگر در لحظه مشخصی، موج در مکان معینی قرار بگیرد، بعد از گذشت زمان، در ناحیه بزرگی پخش خواهد شد. موج، حامل انرژی است. انرژی حمل شده توسط موج در فضا پخش میشود.
چرا ذرات بسیار متفاوت از امواج هستند؟
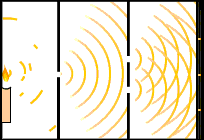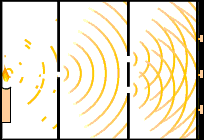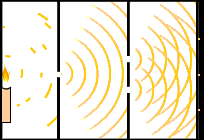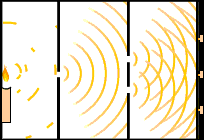
ذرات پس از برخورد در مسیرهای متفاوتی شروع به حرکت خواهند کرد. اما امواج پس از برخورد، بدون تغییر از یکدیگر عبور میکنند. همچنین، به هنگام همپوشانی دو موج با یکدیگر تداخل سازنده یا ویرانگر اتفاق میافتد. اگر قله موج اول با دره موج دوم در یک نقطه به هم برسند، اثر یکدیگر را خنثی خواهند کرد.
این اتفاق به هنگام عبور قسمتی از موج از حفرههای بسیار نزدیک به هم بر روی صفحه، رخ میدهد. امواج در تمامی جهتها پخش میشوند و با یکدیگر تداخل دارند. در نتیجه این تداخل و همپوشانی، در نقاطی از فضا تداخل سازنده و در نقاطی دیگر تداخل ویرانگر رخ میدهد. تصویر نشان داده شده در ادامه آزمایش دو شکاف یانگ را نشان میدهد. به این پدیده پراش میگویند.
در مقابل، به هنگام برخورد مهره یا تیلهای به پرده دو اتفاق رخ میدهد:
- پس از برخورد به عقب برمیگردد.
- از یکی از حفرهها عبور میکند.
در سوی دیگر پرده، مهره مسیر مشخصی را طی خواهد کرد. جهت مسیر بستگی به آن دارد که مهره از کدام حفره خارج شده باشد. پدیده پراش یکی از مشخصههای شناخته شده نور است. اما در اوایل قرن ۲۱، تئوریهای توضیح دهنده تابش نور از اجسام داغ با مشکل مواجه شدند. به این پدیده تابش جسم سیاه گفته میشود. براساس این تئوریها، مقدار انرژی تابیده شده از اجسام داغ در طولموجهای فراتر از نور آبی، بینهایت است. این پدیده به فاجعه فرابنفش معروف است. در نتیجه، این نظریهها باید اصلاح میشدند.
برای اصلاح این تئوریها، دانشمندان فرض کردن که نور علاوه بر موج، گاهی مانند ذرات نیز رفتار میکند. بر طبق این فرضیه، نور پیوسته نیست بلکه از تعداد زیادی ذره تشکیل شده است. بنابراین، نور مانند ذره رفتار میکند. به این ذرات فوتون گفته میشود. اگر نور که به عنوان موج شناخته شده است، مانند ذره نیز رفتار میکند، آیا ذراتی مانند الکترونها و اتمها مانند موج رفتار خواهند کرد؟ برای توضیح ساختار و رفتار اتمها، فرض رفتار موجی ذرات لازم است. اما، آیا الکترونها نیز مانند امواج، به هنگام عبور از حفرههایی با فاصلههای یکسان، پراشیده میشوند؟ در ادامه به این پرسش پاسخ میدهیم.
پراش الکترون و اتم
بر طبق آزمایشهای انجام شده، اتمها مانند موج رفتار میکنند. پردهای با دو حفره نزدیک به هم را در نظر بگیرید. الکترونها با استفاده از تفنگ الکترونی به پرده برخورد میکنند. توزیع الکترونها را در طرف دیگر پرده اندازگیری میکنیم. در سوی دیگر پرده، دو پیک مشاهده نمیشود، بلکه طرح پراش کاملی دیده خواهد شد. این حالت مشابه هنگامی است که نور به پرده برخورد کرده بود.
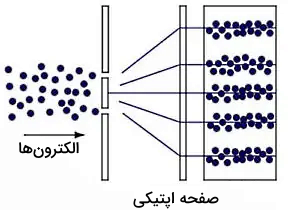
در اینجا، آزمایش یانگ با الکترونها تکرار شده است. رفتار دوگانه موج/ذره شالوده و اساس فیزیک کوانتوم است. حتی میتوان گفت، این نظریه یکی از موفقترین نظریههایی است که در فیزیک ارائه شده است. نکته عجیب در مورد آزمایش پراش الکترونها آن است که انرژی الکترونها در همه نقاط توسط آشکارساز نشان داده نخواهد شد. این حالت مشابه برخورد امواج دریا به ساحل است.
انرژی الکترون در نقطه مشخصی آشکار و در نقطه دیگری آشکار نمیشود. این رفتار شبیه ذره است. بنابراین، در حالی که الکترون مانند موج پراکنده میشود، به هنگام برخورد با نقطه مشخصی بر روی پرده نمایش، ذرهگونه رفتار خواهد کرد. به این رفتار، دوگانگی موج/ذره میگوییم. اما سوالی که مطرح میشود آن است که اگر الکترون یا فوتون مانند موج پراکنده میشوند، اما به هنگام برخورد با نقطه مشخصی به آن انرژی وارد میکنند (مانند ذره)، برای مابقی موج چه اتفاقی خواهد افتاد؟ ناپدید میشود، گویی هرگز وجود نداشته است. این معما منجر به ناراحتی بسیاری از دانشمندان از جمله انیشتین شد. این معما به فروپاشی یا ناپدید شدن تابع موج معروف شده است.
وجود همزمان اجسام در دو جای مختلف
دوگانگی ذره-موج مثالی از برهمنهی است. این بدان معنا است که جسمی کوانتومی همزمان در حالتهای مختلفی وجود دارد. به عنوان مثال، الکترون، همزمان اینجا و آنجا قرار دارد. بنابراین، مکانیک کوانتوم بر پایه احتمالات است. تنها میگوییم جسم با احتمال بیشتری در کدام حالت قرار دارد. این مورد عجیب به صورت ریاضی در قالب تابعی به نابه تابع موج فرمولبندی شده است. به هنگام اندازهگیری یا مشاهده، تابع موج از بین میرود. در این حالت، جسم به اجبار در یکی از حالتهای ممکن قرار میگیرد.
این ایده در ادامه آزمایش فکری معروف گربه شرودینگر است. سرنوشت گربهای در جعبه مهروموم شده به وسیله کوانتومی وصل شده است. این وسیله کوانتومی ذرهای با شانس ۵۰ درصد تجزیه و ۵۰ درصد سالم ماندن است. اگر ذره تجزیه شود، گربه میمیرد. وگرنه، گربه زنده میماند.
چندجهانی
گفتیم تابع موج با مشاهده از بین میرود و انتخابی کوانتومی ایجاد میشود. این ایده به تفسیر کپنهاگ از فیزیک کوانتوم شناخته شده است. اما این تنها گزینه نیست. مدعیان تفسیر چندجهانی بر این باور هستند که هیچ انتخابی وجود ندارد. به جای آن، پس از اندازهگیری، واقعیت به دو کپی شکسته میشود.
- در یکی نتیجه A مشاهده میشود.
- در دیگری نتیجه B دیده خواهد شد.
در مورد چندجهانی و جهانهای موازی در ادامه توضیح خواهیم داد.
مشخصه یابی ستاره ها
فیزیکدان هلندی به نام نیلز بور (Niels Bohr) نشان داد که مدارهای الکترونها داخل اتمها گسسته هستند. این مدارها به نام ترازهای انرژی شناخته میشوند. هنگامی که الکترونی از تراز انرژی بالاتر به تراز انرژی پایینتر برود، فوتونی با انرژی برابر فاصله دو تراز تابیده خواهد شد. همچنین، الکترون با جذب فوتون و استفاده از انرژی آن به تراز انرژی بالاتر میرود.
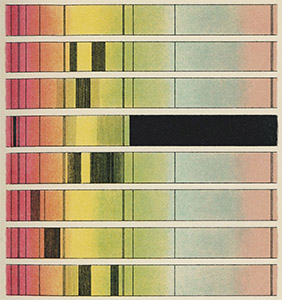
ستارهشناسان از این اثر استفاده بسیاری میکنند. میدانیم، به هنگام عبور نور از منشور، طیف رنگینکمان مانندی متشکل از رنگهای مختلف تشکیل خواهد شد. هنگامی که نور دریافتی از ستارهای تجزیه شود، رنگهای غایب در طیف نشاندهنده بسیاری از ویژگیهای ستاره هستند. عناصر شیمیایی مختلف ترازهای انرژی متفاوتی دارند. بنابراین، با دانستن دقیق رنگهای غایب در طیف، عناصر تشکیل دهنده خورشید و ستارههای دیگر را تعیین میکنیم.
بدون فیزیک کوانتوم خورشید نمیدرخشید
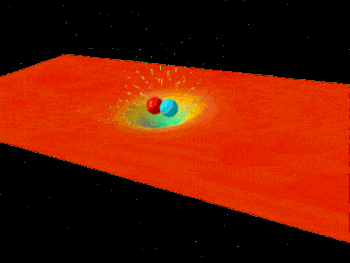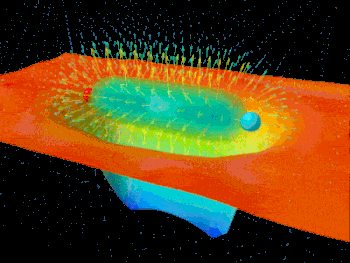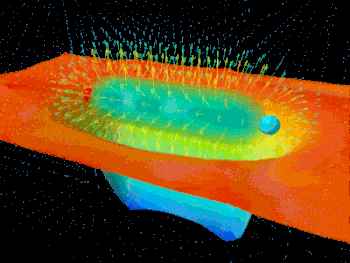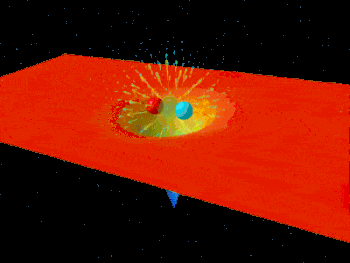
دلیل انرژی زیاد خورشید همجوشی هستهای است. در همجوشی هستهای، دو پروتون به یکدیگر برخورد میکنند. اما، دو پروتون به دلیل داشتن بارهای همنام یکدیگر را دفع میکنند. فیزیکدانها به این نیروی دافعه سد کولنی میگویند. اکنون به این نکته بیاندیشید که پروتونهای مانند دیگر ذرات پس از برخورد با یکدیگر از هم دور میشدند. همجوشی هستهای اتفاق نمیافتاد. در نتیجه، خورشید نور نداشت. اما اگر پروتونها را به صورت موج در نظر بگیریم، قضیه به طور کامل متفاوت میشود. در این هنگام، پروتون به عنوان موج از میان سد کولنی تونل خواهد زد. به این پدیده، تونلزنی گفته میشود.
توقف فروپاشی ستارگان مرده
روزی همجوشی در خورشید تمام خواهد شد. نیروی گرانش پیروز و خورشید از هم فروپاشیده میشود. هر چه خورشید کوچکتر شود، مواد بیشتری درهمفشرده خواهند شد. در اینجا یکی از قوانین مهم فیزیک کوانتوم به نام اصل طرد پائولی وارد بازی میشود. بر طبق این اصل، قرارگیری دو الکترون در حالت کوانتومی یکسان ممنوع است. هنگامی که نیروی گرانش سعی در فروپاشی خورشید یا هر ستاره دیگری دارد، با مقاومتی به نام فشار تبهگنی روبرو میشود.

فروپاشی متوقف و جسمی به نام کوتوله سفید و به اندازه زمین تشکیل خواهد شد. فشار تبهگنی مقاومت بسیار زیادی را وارد میکند. اما اگر کوتوله سفید رشد کند و به جرمی برابر ۱/۴ خورشید برسد، همجوشیهای زیادی همزمان رخ میدهند و کوتوله به قطعههای کوچکی تقسیم میشود. ستارهشناسان به این انفجار ابرنواختر نوع la میگویند.
تبخیر سیاه چاله ها
بر طبق یکی از قوانین کوانتوم به نام اصل عدم قطعیت هایزنبرگ، دانستن دو مشخصه سیستم به طورهمزمان غیرممکن است. هر اندازه یکی از مشخصات را دقیقتر بدانیم، در مورد مشخصه دیگر کمتر اطلاعات داریم. اصل عدم قطعیت در مورد مکان و تکانه یا زمان و انرژی به کار برده می شود.
این حالت، شباهت اندکی به گرفتن وام دارد. شما میتوانید مقدار زیادی پول را برای مدت زمانی کوتاه یا مقدار اندکی را برای زمان طولانیتر قرض بگیرید. اگر انرژی کافی توسط طبیعت قرض گرفته شود، یک جفت ذره به صورت زودگذر به وجود خواهند آمد. اصل عدم قطعیت ما را به سمت ذرات مجازی هدایت میکند. استفان هاوکینگ (Stephen Hawking) تصور کرد که این اتفاق در مرز سیاهچاله رخ میدهد. در آنجا، یک ذره فرار میکند (تابش هاوکینگ)، اما ذره دیگر بلعیده میشود. با گذشت زمان سیاهچاله تبخیر خواهد شد، زیرا تمام آنچه که قرض گرفته بود را به طور کامل پس نداده است.
توضیح ساختار بزرگ جهان
بهترین نظریه برای پیدایش جهان مهبانگ یا Big Bang است. در دهه ۸۰ میلادی تئوری دیگری به نام انبساط یا inflation مطرح شد. در نخستین تریلیونمِ تریلیونمِ تریلیونمِ ثانیه اندازه جهان از حدود سایز اتم به اندازهای در حدود گریپفروت تغییر کرد. یعنی اندازه جهان در حدود بزرگتر شد. اگر گلبول قرمر به همین اندازه بزرگ شود، اندازه آن بزرگتر از تمام جهان قابلمشاهده خواهد شد.
از آنجایی که جهان کوچکتر از اندازه یک اتم بود، در ابتدا نوسانات کوانتومی متصل به اصل عدم قطعیت هایزنبرگ بر آن حاکم بود. انبساط جهان به قدری سریع اتفاق افتاد که نوسانات کوانتومی فرصتی برای محو شدن نیافتند. در نتیجه، انرژی در برخی نواحی جهان بیشتر از جاهای دیگر متمرکز شد.
درهم تنیدگی کوانتومی
انیشتین علاوه بر اثبات رفتار ذرهای نور، در مورد درهمتنیدگی کوانتومی نیز صحبت کرد. امروزه میدانیم درهمتنیدگی واقعی است، اما به طور کامل آن را متوجه نشدهایم. فرض کنید دو ذره را به یکدیگر نزدیک میکنیم به گونهای که حالتهای کوانتومی آنها در قید یکدیگر قرار بگیرند یا درهمتنیده شوند. یکی از ذرات در حالت A و دیگری در حالت B قرار دارند.
بر طبق اصل طرد پائولی، این دو ذره نمیتوانند در حالت یکسانی قرار داشته باشند. اگر یکی را تغییر دهیم، دیگری بلافاصله برای جبران تغییر میکند. حتی هنگامی که دو ذره در دو سوی مخالف جهان از یکدیگر جدا شوند، این اتفاق رخ خواهد داد. اینگونه به نظر میرسد که اطلاعات در مورد تغییری که ایجاد کردهایم بیشتز از سرعت نور بین ذرات جابجا میشود. طبق گفته انیشتین، این امر غیرممکن است.

اثر کوانتومی زنو
در مورد گربه شرودینگر صحبت کردیم. در این آزمایش فکری معروف، گربهای همراه با مادهای رادیواکتیو درون جعبهای حبس شده است. در صورت تجزیه ماده، آشکارساز گاز سمی رها میکند و گربه کشته خواهد شد. اما قبل از آنکه محتوای داخل جعبه را نگاه کنیم، محتویات داخل آن همزمان در دو حالت قرار دارند:
- هیچ تجزیهای رخ نداده و گربه زنده است.
- تجزیه رخ داده و گربه مرده است.
در یک لحظه، زیرچشمی به داخل جعبه نگاه میکنیم. تصمیم گرفته شده و گربه زنده یا مرده است. اما اگر هزاران بار بر ثانیه زیرچشمی به جعبه نگاه کنید و ماده رادیواکتیو را زیر نظر بگیرید، رفتار آن را تغییر خواهید داد. بسته به راهی که جعبه را مشاهده میکنید، دو حالت ممکن است اتفاق بیافتد:
- تجزیه را به تاخیر بیاندازید (اثر کوانتومی زنو).
- تجزیه را سریعتر کنید (اثر کوانتومی ضد زنو).
ذکر این نکته مهم است که اثرات زنو به دلیل اختلال ایجاد شده توسط اندازهگیری اتفاق میافتند.
اثر هونگ-او-مندل
اپتیک کوانتومی در مورد نور و برهمکنش آن با ماده در اندازههای بسیار کوچک است. اثر هونگ-او-مندل در مورد راههای عجیبی است که دو فوتون در جداکننده پرتو با یکدیگر برهمکنش میکنند. جداکننده پرتو وسیلهای اپتیکی است که پرتو نور را به دو قسمت تقسیم میکند. عملکرد آن شبیه منشور است. هنگامی که فوتونی وارد جداکننده میشود، دو حالت اتفاق میافتد:
- فوتون از آن عبور میکند.
- فوتون نوسان میکند.
همانگونه که در تصویر نشان داده شده است، اگر دو فوتون یکسان از هر طرفی وارد تقسیمکننده پرتو شوند، چهار احتمال متفاوت وجود دارند:
- فوتون بالایی منعکس و فوتون پایینی منتقل میشوند.
- هر دو فوتون منتقل میشوند.
- هر دو فوتون منعکس میشوند.
- فوتون بالایی منتقل و فوتون پایینی منعکس میشوند.
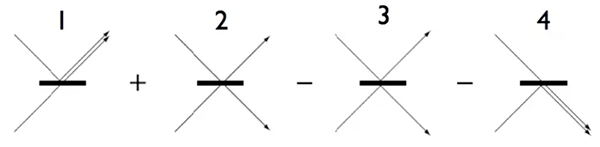
قضیه کمی عجیب به نظر میرسد. زیرا، هر دو فوتون ورود به تقسیمکننده پرتو یکسان هستند. نمیتوانیم احتمال ۲ را از احتمال ۳ تشخیص دهیم. همچنین، دو فوتون یکسان یکدیگر را خنثی میکنند. در نتیجه، احتمالهای ۱ و ۴ تنها نتایج قابل مشاهده هستند. هر دو فوتون در طرف یکسان تقسیمکننده حضور دارند.
انکسار مضاعف خلا
گاهی برای درک مقیاسهای کوچکتر باید به جهان در ابعاد بزرگتری نگاه کنیم. به تازگی، ستارهشناسان با مطالعه ستاره نوترونی بسیار چگال و با درجه مغناطش بسیار بالا، اولین شاهد از اثر کوانتومی به نام انکسار مضاعف خلا را مشاهده کردهاند. این اثر برای نخستین بار در دهه ۳۰ میلادی مطرح شد. طبق پیشبینی فیزیک کوانتوم فضای خالی یا خلا، خالی نیست. در واقع، این فضا سرشار از ذرات مجازی است که در مدت زمان بسیار کوتاهی به وجود میآیند و از بین میروند.
در حالت کلی، انتظار داریم که نور پس از عبور از فضای خالی بدون تغییر باقی بماند. اما اینگونه به نظر میرسد که میدانهای مغناطیسی شدید، مانند میدانهای اطراف ستاره نوترونی، ویژگیهای این ذرات مجازی در خلا را بهبود میبخشند. این بهبود سبب پلاریزاسیون نور عبوری خواهد شد. هنگامی که نور به تلسکوپهای روی زمین میرسد، نتیجه این اثر کوانتومی را در سطح ماکروسکوپی مشاهده میکنیم.
دمای کوانتومی
تصور کنید دمای فر را افزایش و کیکی را برای پختن در آن قرار دادهاید. پس از گذشت مدت زمانی متوجه میشوید که بخشهایی از کیک نپختهاند. زیرا دمای قسمتهایی از فر هنوز دمای اتاق است.
این جمله را بارها شنیدهایم که گرما از نقاط گرمتر به نقاط سردتر منتقل میشود. اما در فیزیک کوانتوم همواره اینگونه نیست. طبق پژوهشهای انجام شده دما در مادهای به نام گرافن رفتار عجیبی از خود نشان میدهد. گرافن ماده عجیب تکلایهای است که از اتمهای کربن ساخته شده است. الکترونهای حامل گرما به صورت موج پراکنده میشوند. به هنگام انتقال گرما در گرافن نقاطی از آن سردتر از نقاط دیگر باقی میمانند.
نکته هیجانانگیز آن است که اندازه این موجها قابل کنترل هستند و با استفاده از میکروسکوپهای گرمایی مشاهده میشوند. بنابراین، دانشمندان به دیدگاه مناسبی در مورد دما در مقیاس کوانتومی میرسند. در صورت مهار این اثر، میتوان از آن در محاسبات، پزشکی و نظارت زیستمحیطی استفاده کرد.
تاکنون با اثرات مختلف فیزیک کوانتوم و موردهای عجیب این شاخه از فیزیک آشنا شدیم. در ادامه در مورد تابش جسم سیاه، تابع موج شرودینگر، اصل عدم قطعیت هایزنبرگ، جهانهای موازی و کاربردهای فیزیک کوانتوم در شاخههای مختلف علوم صحبت خواهیم کرد.
تابش جسم سیاه
اجسام با دمای پایینتر انرژی کمتر و اجسام با دمای بالاتر انرژی بیشتری را ساطع میکنند. هنگامی که دمای جسمی افزایش مییابد، طول موج تابیده شده از فروسرخ به قرمز و سپس از قرمز به نارنجی تغییر میکند. دمای جسم تابشکننده تعیین کننده طول موجی است که در آن انرژی تابیده شده بیشینه خواهد بود. به عنوان مثال، دمای سطح خورشید در حدود ۵۰۰۰ تا ۶۰۰۰ درجه کلوین است. از این رو، شدت تابش آن در محدود طول موجهای ۵۶۰ نانومتر از طیف الکترومغناطیسی بیشتر است. دمای بدن انسان در حالت عادی در حدود ۳۰۰ کلوین است. بنابراین، شدت تابش آن در محدوده فروسرخ طیف الکترومغناطیسی بیشتر است.
قسمتی از تابش تابیده بر روی جسم جذب و قسمتی از آن منعکس میشود. در تعادل ترمودینامیکی، نرخ جذب تابش توسط جسم برابر با نرخ ساطع شدن تابش توسط آن است. یک جاذب ایدهآل تمام تشعشع الکترومغناطیسی تابیده شده بر آن را جذب میکند. به چنین جسمی، جسم سیاه گفته میشود. جسم سیاه حالت ایدهآلی برای فیزیک است. در واقع هیچ جسم فیزیکی، ۱۰۰ درصد تابش وارد شده را جذب نخواهد کرد. با ایجاد حفرهای کوچک در دیواره کاواک (تصویر نشان داده شده در ادامه) میتوانیم جسم سیاهی نزدیک به حالت ایدهآل درست کنیم.
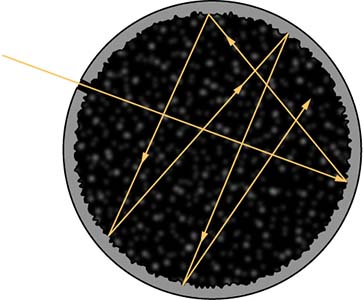
دیوارههای داخلی کاواک زبر و سیاه هستند. بنابراین، هر تابشی که از طریق حفره کوچک وارد کاواک میشود، داخل آن گیر خواهد کرد. در تعادل ترمودینامیکی (در دمای T)، دیوارههای کاواک هر مقدار تابشی را که جذب کردهاند. ساطع خواهند کرد. همچنین، در داخل کاواک تشعشع وارد شده به حفره برابر با تابش خارج شده از آن است. طیف تابشی جسم سیاه با استفاده از تحلیل نور تابیده شده از حفره به دست میآید. به امواج الکترومغناطیسی تابیده شده از جسم سیاه تابش جسم سیاه گفته میشود. شدت تابش جسم سیاه به طول موج تشعشعات ساطع شده و دمای جسم سیاه بستگی دارد.
تابع شدت تابش بر واحد طول موج است. به بیان دیگر، این تابع به صورت توان تابش شده بر واحد سطح بر واحد طول موج تعریف میشود.
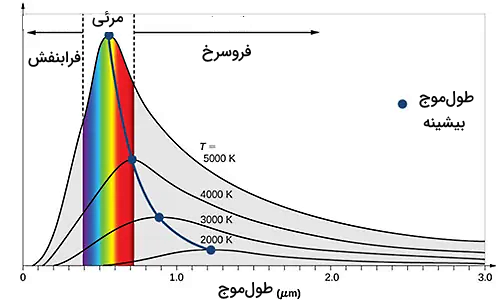
بر طبق این تعریف، توان تابش منتشر شده بر واحد سطح بین طول موجهای و است. در حالت کلی، تابش منتشر شده توسط مواد مختلف شبیه نمودار تابش جسم سیاه است. تصویر ۱، شدت تابش جسم سیاه بر حسب طول موج را در دماهای مختلف نشان میدهد. با افزایش دمای جسم سیاه، شدت تابش نیز افزایش یافته است. همچنین، پیک شدت تابش با افزایش دما به سمت طول موجهای کوتاهتر حرکت کرده است. دانشمندان در آزمایشهای انجام شده برای مطالعه جسم سیاه، به دو قانون مهم رسیدهاند:
- جابجایی وین
- قانون استفان
قانون جابجایی وین
جابجایی وین در تصویر ۱ با متصل کردن بیشینههای شدت نشان داده شده است. هر چه جسمی داغتر باشد (دمای بالاتر)، طول موج شدت بیشینه کوتاهتر خواهد بود. رابطه ریاضی جابجایی وین به صورت زیر نوشته میشود:
در رابطه فوق مکان شدت بیشینه در نمودار تابش است. به بیان دیگر، طول موجی است که در آن شدت تابش جسم سیاه در دمای خاص، بیشینه خواهد بود. به این نکته توجه کنید که دما بر حسب کلوین است. با استفاده از جابجایی وین میتوانیم دمای ستارگان دوردست را اندازه بگیریم.
مثال جابجایی وین
اگر در نیمکره شمالی زندگی میکنید، در زمستان به هنگام نگاه کردن به آسمان ممکن است صورتفلکی شکارچی را مشاهده کنید. رنگ یکی از ستارهها (ستاره ۱) در این صورت فلکی آبی و رنگ ستاره دیگر (ستاره ۲) قرمز است. کدامیک از این دو ستاره سردتر هستند؟

پاسخ
با هر ستاره مانند جسم سیاه رفتار میکنیم. در نتیجه، بر طبق قانون وین، دمای آن متناسب با عکس طول موج شدت تابش است. طول موج نور آبی کوتاهتر از طول موج نور قرمز است. حتی اگر مقدار دقیق طول موجها را ندانیم، باز هم میتوانیم تناسب را برقرار کنیم. رابطه وین را برای ستاره آبی و قرمز مینویسیم. بنابراین، داریم:
با سادهسازی رابطه بالا داریم:
بنابراین، ستاره قرمز سردتر از ستاره آبی است. به این نکته توجه داشته باشید که بر طبق قانون وین، هر چه دمای جسم تابشی بالاتر باشد، طول موج تابش آن کوتاهتر است. تحلیل کیفی نشان داده شده در این مثال برای هر جسم تابشی صحیح خواهد بود.
قانون استفان
دومین رابطه به دست آمده از آزمایش، قانون وین است. این قانون در مورد کل توان تابشی ساطع شده از جسم سیاه در تمام طول موجهای طیف در هر دمایی است. با افزایش دمای جسم سیاه، توان تابشی کل نیز افزایش خواهد یافت. رابطه ریاضی قانون استفان به صورت زیر نوشته میشود:
A = مساحت سطح جسم سیاه
T = دمای جسم سیاه بر حسب کلوین
= ثابت استفان - بولتزمن
مقدار برابر است. با استفاده از این قانون میتوانیم مقدار انرژی ساطع شده از ستاره را با اندازهگیری دمای آن، تخمین بزنیم.
مثال قانون استفان
اندازه کوتوله سفید در حدود زمین و دمای سطح آن برابر است. دمای سطح غول سرخ نوعی برابر و شعاع آن در حدود ۱۰۰۰۰۰ برابر بزرگتر از کوتوله سفید است. توان متوسط تابشی بر واحد سطح و توان کل تابیده شده توسط این ستارهها چقدر است؟ چگونه با یکدیگر مقایسه میشوند؟
پاسخ
اگر با ستاره مانند جسم سیاه رفتار کنیم، بر طبق قانون استفان ، توان کلی که ستاره ساطع میکند متناسب با توان چهارم دمای آن است. برای یافتن توان تابیده شده بر واحد مساحت سطح، نیاز به ساختن فرضیه در مورد شکل ستاره نیست. زیرا نسبت توان به سطح تنها به دما بستگی دارد. اما، برای محاسبه توان کل، فرض میکنیم که انرژی از سطح کروی دربرگیرنده ستاره تابش خواهد کرد. بنابراین، مساحت برابر است.
برای به دست آوردن توان متوسط بر واحد سطح داریم:
توان تابش شده توسط کوتوله سفید در حدود ۵۰۰۰ برابر توان تابیده شده توسط غول قرمز است. با دانستن این نسبت، داریم:
دیدیم که توان کل تابیده شده توسط کوتوله سفید درصد کوچکی از توان کل تابیده شده توسط غول قرمز است. به منظور تخمین مقدار مطلق توان تابیده شده بر واحد سطح از قانون استفان استفاده میکنیم. برای کوتوله سفید داریم:
با مقیاسبندی نتیجه برای کوتوله سفید، نتیجه مشابهی برای غول قرمز به دست میآید:
نمودار تابش جسم سیاه به طور آزمایشی شناخته شده بود، اما شکل آن تا سال ۱۹۰۰ توضیح فیزیکی نداشت. مدل فیزیکی جسم سیاه در دمای T همان امواج الکترومغناطیسی محصور شده داخل کاواک و تعادل ترمودینامیکی با دیوارههای آن است. امواج با دیوارهها تبادل انرژی میکنند.
مساله مهم در اینجا به دست آوردن توزیع چگالی انرژی در میان مدهای مختلف نوسان در طول موجهای متفاوت است. به بیان دیگر، دانستن مقدار انرژی حمل شده توسط تک طول موج یا دستهای از طول موجها بسیار مهم است. با دانستن توزیع انرژی، نمودار تابش جسم سیاه، قانون استفان و قانون جابجایی وین را با استفاده از روشهای آماری استاندارد به دست خواهیم آورد. هنگامی که مدل فیزیکی ارائه شده صحیح باشد، توضیحات نظری باید منطبق بر نمودارهای تجربی باشند.
توضیح پلانک در مورد فاجعه فرابنفش
فیزیک کلاسیک در توضیح نمودار تجربی تابش جسم سیاه ناتوان ماند. در فیزیک کلاسیک، تابش به صورت امواج در نظر گرفته میشوند. مدهای امواج الکترومغناطیسی محبوس شده در کاواک با دیوارههای کاواک به طور پیوسته تبادل انرژی دارند و با آنها در تعادل ترمودینامیکی هستند. در اینجا تبادل انرژی به صورت پیوسته در نظر گرفته شده است. تصویر کلاسیکی پایه مدل ارائه شده توسط ریلی و جینز است. همانگونه که در تصویر زیر نشان داده شده است، قانون ریلی-جینز در بازتولید نتایج تجربی ناموفق ماند.
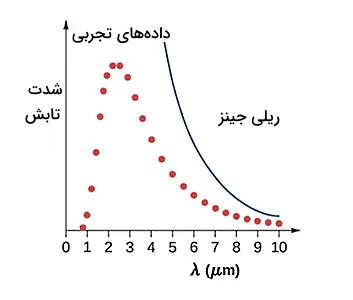
در طول موجهای کوچک، نظریه ریلی-جینز شدت تابش بینهایت را پیشبینی میکند. این پیشبینی در تناقض با یافتههای تجربی است. بر طبق آزمایشهای انجام شده، مقدار شدت تابش در ناحیه فرابنفش طیف محدود است. این واگرایی بین نتایج فیزیک کلاسیک و آزمایشهای تجربی (فاجعه فرابنفش)، نشاندهنده ناتوانی فیزیک کلاسیک در توضیح کارکرد تابش جسم سیاه است.
فاجعه فرابفش: قانون ریلی- جینز قادر به توضیح طیف تابشی جسم سیاه نیست.
این مشکل توسط ماکس پلانک در سال ۱۹۰۰ حل شد. او برای حل این مشکل از روش ارائه شده توسط ریلی و جینز استفاده کرد. اما، ایده جدید ارائه شده توسط پلانک استفاده از فرضیه نوسانهای اتمی بود. بر طبق این فرضیه، منشا تابش داخل کاواک نوسانات اتمی داخل دیوارهها است. مقادیر انرژی این نوسانها گسسته هستند. بنابراین، تبادل انرژی بین تشعشع محبوس شده داخل دیوارههای کاواک و دیواره، در مقادیر مشخصی از انرژی صورت خواهد گرفت. بر طبق فرضیه پلانک در مورد مقدارهای گسسته انرژی، نوسانگرها داخل کاواک انرژی گسسته دارند. این نظریه فراتر از فیزیک کلاسیک بود. بر طبق فیزیک کلاسیک، انرژی نوسانگر هر مقداری را میتواند داشته باشد. در نتیجه این فرضیه، انرژی به صورت زیر نوشته خواهد شد:
در رابطه فوق، f فرکانس نوسانگر پلانک است. به n عدد کوانتومی میگوییم. همچنین، h ثابت فیزیکی به نام ثابت پلانک است و مقدار آن برابر است با:
هر مقدار انرژی گسسته مطابق با یک حالت کوانتومی نوسانگر پلانک است. حالتهای کوانتومی توسط عدد n شمارهگذاری میشوند. به عنوان مثال، اگر نوسانگر پلانک در اولین حالت کوانتومی خود باشد، یعنی n=۱، انرژی ان برابر hf خواهد بود. اگر در حالت کوانتومی دوم باشد، یعنی n=۲، انرژی آن برابر 2hf است.
همانگونه که میبینید تعداد حالتهای کوانتومی بینهایت است و به صورت سری زیر نوشته میشوند:
در مجموعه فوق، هر دو حالت کوانتومی به دنبال هم توسط شکاف انرژی برابر E=hf از هم جدا شدهاند. نوسانگر داخل دیواره میتواند از تابش داخل کاواک، انرژی کسب کند (جذب) یا انرژی از دست بدهد (نشر). طی روند جذب، نوسانگر به حالت کوانتومی بالاتر میرود. در مقابل، هنگام نشر، نوسانگر به حالت کوانتومی پایینتر فرستاده میشود. ذکر این نکته مهم است که حد بالایی برای میزان انرژی مبادله شده وجود ندارد. اما هر چه مبادله شود باید ضریب صحیحی از hf باشد. در صورتی که مقدار بسته انرژی متفاوت باشد، نه جذب و نه منتشر خواهد شد.
همانگونه که در مطلب «امواج چیست ؟ — به زبان ساده» گفتیم، فرکانس موج متناسب با طول موج آن بر سرعت انتشار موج است. برای تابش الکترومغناطیسی سرعت انتشار موج برابر سرعت نور یعنی c است.
برای محاسبه چگالی انرژی جسم سیاه از فرضیه پلانک استفاده میکنیم. بر طبق این فرضیه، شدت توان تابیده شده بر واحد طول موج به صورت زیر به دست خواهد آمد:
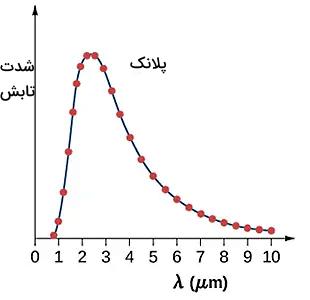
در رابطه فوق، c سرعت نور در خلا و ثابت بولتزمن و برابر است. به این رابطه، قانون تابش جسم سیاه پلانک گفته میشود. این قانون به خوبی نتایج تجربی و نمودار تابش جسم سیاه را توضیح میدهد. همچنین، قانونهای جابجایی وین و استفان از این رابطه به دست میآیند. برای به دست آوردن قانون جابجایی وین، با استفاده از حساب دیفرانسیل مقدار بیشینه نمودار شدت تابش را به دست میآوریم. همچنین، برای به دست آوردن قانون استفان و مقدار ثابت استفان - بولتزمن، انتگرال استفاده میکنیم. نتیجه نظری پلانک (نمودار پیوسته) و نمودار تجربی تابش جسم سیاه (نمودار نقطهای) به خوبی بر یکدیگر منطبق هستند.
مثال نوسانگر کوانتومی پلانک
نوسانگر کوانتومی داخل دیواره کاواک با فرکانس نوسان میکند. فاصله بین ترازهای انرژی را به دست اورید.
پاسخ
فاصله بین دو تراز انرژی متوالی به صورت زیر به دست خواهد آمد:
در سال ۱۹۶۵، تابش پسزمینه مایکروویو کیهانی (cosmic microwave background radiation یا CMBR) توسط پنزیاس (Penzias) و ویلسون (Wilson) کشف شد. طیف تابشی اندازهگیری شده برای آن به طور قابلملاحظه و شگفتانگیزی مطابق با نمودار تابش جسم سیاه در دمای ۲/۷۲۵ کلوین بود. با تحلیل این طیف به این نتیجه رسیدند که جهان در حال انبساط و سرد شدن است.
معادله موج شرودینگر چیست؟
معادله شرودینگر یا معادله موج شرودینگر، معادله دیفرانسیل جزیی است که دینامیک سیستم فیزیک کوانتوم را با استفاده از تابع موج توصیف میکند. مسیر، موقعیت و انرژی این سیستمها با حل معادله شرودینگر به دست خواهند آمد. ذکر این نکته مهم است که اطلاعات به دست آمده در مورد موقعیت و تکانه، بر پایه احتمالات است.
تمام اطلاعات ذره ریز اتمی داخل تابع موج نهفته است. تابع موج با حل معادله شرودینگر به دست خواهد آمد. معادله شرودینگر یکی از بدیهیات اساسی است که به دانشجویان فیزیک دوره کارشناسی آموزش داده میشود. این معادله توسط اروین شرودینگر (ٍErwin Schrodinger) برنده جایزه نوبل در سال ۱۹۳۳، به دست آورده شد.
با درک معادله شرودینگر به این نتیجه خواهید رسید که قوانین حاکم بر فیزیک کلاسیک بسیار متفاوت از قوانین حاکم بر فیزیک کوانتوم است. معادله موج شرودینگر با استفاده از قانون پایستگی انرژی اطلاعاتی در مورد رفتار الکترون مقید در هسته میدهد. این اطلاعات با استفاده از تابع موج شرودینگر به دست خواهند آمد. اما سوالی که ممکن است مطرح شود ان است که حل معادله شرودینگر علاوه بر دادن اطلاعاتی در مورد الکترون مقید به هسته، موقعیت و تکانه الکترون، چه اطلاعات دیگری به ما خواهد داد؟ با حل این معادله، در مورد شکل و جهت اوربیتالهای داخل اتم یا مولکول اطلاعاتی را به دست خواهیم آورد. حل دقیق این معادله تنها برای هستهای با یک الکترون مانند H انجام شده است.
تابع موج شرودینگر چیست؟
تابع موج یکی از مهمترین مفاهیم مکانیک کوانتوم است. زیرا هر ذرهای با تابع موج نمایش داده میشود. تابع موج با حرف لاتین psi یا نوشته خواهد شد. این تابع به موقعیت و زمان وابسته است. هنگامی که تابع موج ذرهای را داشته باشیم، تمام اطلاعات لازم در مورد سیستم فیزیکی را خواهیم داشت. همچنین، تمام اندازههای مختلف برای کمیتهای قابل مشاهده با اعمال عملگر بر آن به دست میآید.
احتمال یافتن ذره در مکان x و زمان t با مربع تابع موج نشان داده میشود. البته تابع موج باید نرمال شده باشد، یعنی جمع مربع آن بر روی تمام مکانهای ممکن برابر یک باشد. این جمله بدان معنا است که ذره به طور حتم در جایی در فضا قرار گرفته است. باید بدانید که اطلاعات داده شده توسط موج براساس احتمالات هستند. بنابراین، نتیجه مشاهدات قابل پیشبینی نیستند.

با استفاده از تابع موج مقدار چشمداشتی مکان ذره را در زمان t محاسبه میکنیم. مقدار چشمداشتی، مقدار متوسط x پس از تعداد زیادی اندازهگیری است. باز هم یادآور میشویم که اندازهگیری دقیق امکانپذیر نیست. با استفاده از عملگرهای مناسب، مقدارهای چشمداشتی برای تکانه، انرژی و هر کمیت قابلمشاهده دیگری را نیز به دست خواهیم آورد.
رابطه ریاضی معادله موج شرودینگر چیست ؟
معادله موج شرودینگر معادله موجی برای تابع موج ذره است. این معادله با استفاده از قانون پایستگی انرژی استخراج شده است. در این معادله از عملگری به نام همیلتونی استفاده میشود. سادهترین شکل ریاضی این معادله به صورت زیر نوشته میشود:
= ثابت پلانک تقسیم بر
H = عملگر هامیلتونی، که جمع انرژی جنبشی و انرژی پتانسیل سیستم کوانتومی است.
عملگر هامیلتونی، عبارت طولانی است. با جایگذاری صورت کامل آن در معادله شرودینگر خواهیم داشت:
این نکته را به یاد داشته باشید که در مسائل سهبعدی، مشتق جزئی با عملگر لاپلاس () جایگزین خواهد شد.
معادله شرودینگر وابسته به زمان
معادله موج شرودینگر وابسته به زمان، حالت کلیتر معادله موج بیان شده در قسمت قبلی است. سادهترین حالتی که میتوان در نظر گرفت ذره آزاد است، زیرا پتانسیل آن برابر صفر خواهد بود. با حل این معادله به جواب زیر برای تابع موج خواهیم رسید:
تابع موج به دست آمده به شکل موج تخت است. در رابطه به دست آمده k برابر و برابر است. برای حالتهای دیگر، تابع پتانسیل نقش مهمی در معادله شرودینگر خواهد داشت و بیانگر شرایط مرزی برای قسمت فضایی تابع موج است.
معادله موج شرودینگر مستقل از زمان
برای حالتهای ایستا یا جوابهایی به شکل امواج ایستاده (مانند دیوار پتانسیل و ذره در جعبه)، معادله شرودینگر به دو قسمت فضایی و زمانی تقسیم خواهد شد:
با جایگذاری رابطه فوق در صورت اصلی معادله شرودینگر، عبارتهای زمانی از طرفین ساده خواهند شد و معادله مستقل از زمان تابع موج به صورت زیر به دست میآید:
در عبارت فوق، E انرژی سیستم و H عملگر هامیلتونی است. شکل دقیقتر معادله شرودینگر مستقل از زمان به صورت زیر نوشته میشود:
قسمت زمانی معادله به صورت زیر است:
تابع موج چگونه اعداد کوانتومی را تولید میکند ؟
گفتیم با حل معادله شرودینگر یا تابع موج را به دست میآوریم. شرایط مرزی که به هنگام حل معادله شرودینگر اعمال کردهایم اعداد کوانتومی را تولید میکنند. اما سوالی که ممکن است مطرح شود آن است شرایط مرزی کدام موارد هستند:
- و اولین مشتق آن باید پیوسته باشند.
- باید بهنجار شده باشد. این بدان معنا است که با احتما ۱۰۰ درصد الکترون جایی در جهان قرار دارد. برای مقدار حقیقی ، شرط بهنجار به صورت زیر خواهد بود:
- با افزایش فاصله نسبت به هسته، الکترون از قید آن آزاد خواهد شد.
تابع موج الکترون در سهبعد وجود دارد. بنابراین، حلهای معادله شرودینگر سه قسمت دارند. معادله را با استفاده از روشی مرسوم در معادلات دیفرانسیل به نام جداسازی حل میکنیم:
پس از جایگذاری عبارت فوق در معادله مستقل از زمان شرودینگر، شروط زیر باید برقرار باشند:
- در R(r)، ثابتی به نام n مقدارهای ۱، ۲، ۳، ۴ و ... را خواهد داشت.
- در ثابتی به نام l مقدارهای ۰، ۱، ۲، ۳، ... و (n-1) را خواهد داشت.
- در ، ثابتی به نام m مقدارهای l- تا l را خواهد داشت.
بنابراین، با استفاده از تابع موج به دست آمده از معادله شرودینگر، سه عدد کوانتومی توصیف کننده ویژگی رفتاری الکترون در اتم به دست آمدند.
- n: عدد کوانتومی اصلی است.
- l: عدد کوانتومی مربوط به اوربیتال موردنظر.
- m: عدد کوانتومی مغناطیسی.
اصل عدم قطعیت چیست؟
در زندگی روزمره، محاسبه سرعت و مکان جسمی متحرک آسان است. به عنوان مثال، اگر سرعت اولیه و نهایی جسمی و مدت زمان تغییر سرعت را بدانیم، شتاب حرکت آن را به آسانی با استفاده از معادلههای حرکت بر خط راست به دست خواهیم آورد. اما در فیزیک کوانتوم، این محاسبات به دلیل رابطه ریاضی بنیادی به نام اصل عدم قطعیت سرراست نخواهند بود.
این اصل توسط فیزیکدان آلمانی به نام هایزنبرگ در سال ۱۹۲۷ فرمولبندی شد. بر طبق این اصل، دانستن مقدار دقیق سرعت و مکان ذرهای مانند فوتون یا الکترون امکانپذیر نیست. هر اندازه در مورد مکان ذره دقیقتر باشیم، در مورد سرعت آن کمتر خواهیم دانست.
به منظور فهم بهتر ایده حاکم بر اصل عدم قطعیت، موجکی را در استخری در نظر بگیرید. برای اندازهگیری سرعت این موجک، مسیر قلهها و درههای مختلفی را دنبال میکنیم. هر چه تعداد پیکها و قلههای عبوری بیشتر باشد، سرعت موجک را با دقت بیشتری اندازه خواهیم گرفت. اما، در مورد مکان آن حرف کمتری برای گفتن داریم. مکان موجک بین قلهها و درههای آن پخش شده است. برعکس، اگر به دنبال یافتن مکان دقیق یکی از پیکهای موج هستیم، باید بخش کوچکی از موج را دنبال کنیم. بنابراین، اطلاعات زیادی در مورد سرعت موج را از دست خواهیم داد.
ترن هوایی نشان داده شده در تصویر زیر را در نظر بگیرید. هنگامی که این ترن به قله میرسد، از آن عکس میگیریم. در نتیجه، مکان آن را میدانیم. اما با داشتن عکس در مورد سرعت حرکت ترن اطلاعاتی نخواهیم داشت.

هنگامی که ترن به سمت پایین حرکت میکند، سرعت آن را بر حسب زمان اندازه میگیریم. اما در مورد مکان آن اطلاعات کمی در دست داریم. اصل عدم قطعیت مبادلهای بین دو متغیر مکمل مانند مکان و سرعت است.

این اصل در فیزیک کوانتوم نقش مهمی را ایفا میکند. زیرا همانگونه که در مطالب بالا اشاره شد ذراتی مانند الکترون علاوه بر رفتار ذرهای، مانند موج نیز رفتار میکنند. بیشتر افراد به هنگام مطالعه این اصل اشتباه مشترکی را مرتکب میشوند. اصل عدم قطعیت هایزنبرگ میگوید عدم قطعیت ذاتی در اندازهگیری متغیر ذره وجود دارد. این عدم قطعیت به طور معمول در مورد مکان و تکانه یا انرژی و زمان مشاهده میشود. این اصل، تئوری بنیادی در فیزیک کوانتوم است و به دلیل وجود آن نمیتوان چندین متغیر کوانتومی را همزمان اندازهگیری کرد.
مثال اول اصل عدم قطعیت
عدم قطعیت در تکانه توپ فوتبالی که توسط علی با سرعت ۴۰ متر بر ثانیه پرتاب میشود برابر است. عدم قطعیت مکان توپ را به دست آورید. جرم توپ را برابر ۰/۴۰ کیلوگرم در نظر بگیرید.
پاسخ
با دانستن سرعت و جرم توپ فوتبال، تکانه آن را به دست میآوریم:
برای عدم قطعیت تکانه داریم:
اکنون عدم قطعیت در مکان توپ را به دست میآوریم:
به این نکته توجه داشته باشید که .
مثال دوم اصل عدم قطعیت
موقعیت یون کلر در مادهای مشخص با حداکثر خطایی برابر یک میکرومتر تعیین میشود. اگر جرم این یون برابر ، اندازه خطای اندازهگیری سرعت را به دست آورید.
پاسخ
خطای اندازهگیری سرعت برابر است با:
در نتیجه، طبق رابطه عدم قطعیت هایزنبرگ داریم:
فیزیک کوانتوم و جهان های موازی
یکی از عجیبترین ایدههای فیزیک کوانتوم وجود جهانهای موازی است. بر طبق تفسیر تفسیر چندجهانی (Many-Worls Interpretation یا MWI) تعداد زیادی جهان به طور موازی در زمان و فضایی مشابه زمان و فضای ما وجود دارند. اما ذکر این نکته مهم است که تئوری جهانهای موازی به عنوان یکی از چالش برانگیزترین تئوریها در علم باقیمانده است.
جهان ما بسیار بزرگ است. صدها میلیارد کهکشان در فضا میچرخند. هر کهکشان، میلیاردها ستاره دارد. پژوهشهای زیادی در مورد اندازه جهان انجام شده است. بر طبق برخی از پژوهشهای انجام شده، اندازه جهان میتواند در حدود هفت میلیارد سال نوری باشد. حتی بعضی از پژوهشها اندازه جهان را بینهایت عنوان کرده اند. ایده چندجهانی در سال ۱۹۵۷ توسط اورت (Everett) مطرح شد. بر طبق این ایده، علاوه بر جهانی که میشناسیم و در آن زندگی میکنیم، هزاران جهان در کیهان وجود دارند. هر زمانی که آزمایش کوانتومی با نتایج ممکنِ متفاوت انجام شود، همه نتیجههای حاصل، هر کدام در جهان جدیدی به دست آمدهاند.
نظریههای مختلفی در مورد فرضیه چندجهانی وجود دارد. اگر درک فرضیهای سخت باشد، حس اتلاف وقت را تجربه خواهیم کرد. اما اگر درک فرضیه موردمطالعه بسیار آسان باشد، چندجهانی بسیار جالب به نظر خواهد رسید. به طور معمول، چندجهانی و جهانهای موازی در مباحث فیزیکی مهبانگ، نظریه ریسمان و فیزیک کوانتوم بحث میشود.
جهان های موازی بر پایه نظریه مه بانگ
در حدود ۱۳/۷ میلیارد سال قبل، هر آنچه که در مورد آن میدانیم در نقطه بسیار کوچکی جمع شده بودند. بر طبق تئوری مهبانگ یا بیگبنگ، این نقطه منفجر و تورمی سریعتر از سرعت نور در تمام جهتها و در کسری از ثانیه رخ داد. برای سادهسازی نقطه کوچکی را در وسط کاغذ سفیدی در نظر بگیرید. این نقطه شامل تمامی آنچه اکنون میشناسیم در ابتدای هستی است. در کمتر از ، این نقطه منفجر و اندازهاش در حدود برابر اندازه اولیه میشود. هنگامی که سرعت منبسط شدن یا تورم کاهش یافت، سیل ماده و تشعشع ظاهر شد و اتمها، مولکولها، ستارهها و کهکشانها شروع به تشکیل شدن کردند.

روند رمزآلود مهبانگ و تورم، تعدادی از پژوهشگران را به سمت چندجهانی سوق داد. بر طبق صحبت فیزیکدان نظری به نام «الکساندر ویلنکین» (Alexander Vilenkin) از دانشگاه Tufts، تورم در همهجا، در یک لحظه پایان نیافته است. در حالیکه در نقطهای از کیهان به اتمام رسیده است، در جاهای دیگر ادامه دارد. این حالت به عنوان نظریه تورم ابدی شناخته شده است. بنابراین، هنگامی که تورم در نقطه مشخصی به پایان رسیده است، جهان حبابی جدیدی تشکیل شده است.
این جهانهای حبابی با یکدیگر ارتباطی نخواهند داشت. زیرا به طور نامحدود گسترده میشوند. اگر به دنبال رسیدن به حباب بعدی یا مشخص کردن لبه و مرز هر جهان هستیم، موفق نخواهیم شد. زیرا لبهها سریعتر از سرعت نور از ما دور خواهند شد. اما تصور کنید به حباب بعدی یا به لبه جهان موازی دیگر رسیدهایم، چه اتفاقی خواهد افتاد؟
بر طبق نظریه تورم ابدی (که با نظریه ریسمان ترکیب شده است)، جهان آشنایی که در آن زندگی میکنیم همراه با تمام ثابتهای فیزیکی و شرایط زندگی به طور کامل متفاوت با جهان فرضی دیگر خواهد بود.

جهان های موازی بر پایه کوانتوم فیزیک
برخی از محققان ایده جهانهای موازی را بر پایه فیزیک کوانتوم قرار دادهاند. در فیزیک کوانتوم، وجود حالتهای مختلف برای ذرات ریز به طورهمزمان ممکن است. همانگونه که در بخش معادله موج شرودینگر گفته شد، تابع موج حاوی تمامی این حالتهای ممکن با احتمالهای متفاوت است. اما به هنگام مشاهده، تنها یکی از این حالتهای ممکن را مشاهده میکنیم. بر طبق تفسیر کپنهاگی فیزیک کوانتوم، هنگامی نتیجه را مشاهده میکنیم که تابع موج به واقعیت واحدی فروپاشی کند.
اما نظریه جهانهای موازی مساله را به گونه متفاوتی بیان میکند. بر طبق این نظریه، هر زمانی که حالت یا نتیجهای مشاهده شود، نتیجه کوانتومی متفاوتی در جهانی دیگر به واقعیت تبدیل خواهد شد. این حالت آرایش انشعابی است که در آن لحظه به لحظه جهانی که درک کردهایم به جهانهای جایگزین وصل خواهد شد. جهانهای جایگزین به طور کامل جدا شدهاند. بنابراین، ممکن است تعداد بیشماری از خودتان، زندگی کمی یا به طور کامل متفاوتی را تجربه میکنید و حتی از این موضوع خبر ندارید.
این نظریه یکی از سرراستترین نظریههای مطرح شده در مکانیک کوانتومی است. اما مانند هر نظریه دیگری مشکلاتی دارد. یکی از مشکلات قابل جعل نبودن آن است. اگر نظریهای مطرح شود و هیچ آزمایش یا مشاهدهای برخلاف آن یافت نشود، نکته منفی به نسبت بزرگی برای آن نظریه خواهد بود.
همانگونه که گفتیم جهانی که در آن زندگی میکنیم دو حالت دارد:
- بسیار بزرگ و محدود است.
- بسیار بزرگ و نامحدود است.
هر دو حالت فوق امکانپذیر هستند. اما اگر جهان نامحدود باشد، فرض دیگری نیز وجود خواهد داشت. ماده با استفاده از راههای زیادی در جهان نامحدود قرار میگیرد. در نهایت، ماده باید با استفاده از راههای مشابهی خود را تکرار و مرتب کند. بنابراین، اگر جهان نامحدود باشد، امکان وجود جهانهای موازی نامحدود نیز وجود خواهد داشت.
برای سادهسازی، جهان را به صورت دستهای کارت در نظر بگیرید. کارتها پس از هر بار بر زدن با ترتیب متفاوتی قرار میگیرند. اگر تعداد بر زدنها را زیاد کنید، ممکن است ترتیب قرار گرفتن کارتها تکرار شود. به طور مشابه، اگر جهان نامحدود و تعداد حالتهای ماده محدود باشد، تعداد راههایی که ماده خود را مرتب میکند تکرار خواهند شد. بر طبق پژوهشهای انجام شده در سالهای اخیر، جهانی که در آن زندگی میکنیم شاید یکی از چندین جهان از جهانهای موازی باشد. در نتیجه، تمام زندگی ما ممکن است در جای دیگری در جهان تکرار شده باشد.
اما اگر جهان از نقطه محدودی آغاز شده باشد، نسخه جایگزینی از ما ممکن است وجود نداشته باشد.
نظریه های موافق چندجهانی
تعدادی از نظریهها موافق چندجهانی یا جهانهای موازی هستند. این نظریههای عبارنتد از:
- تورم کیهانی: جهان ما در اولین لحظههای پیدایش به صورت نمایی منبسط شد. اما آیا این انبساط یکنواخت بود؟ در صورتی که پاسخ به این پرسش خیر باشد، ناحیههای متفاوتی از فضا با نرخهای مختلف رشد کردند و ممکن است از یکدیگر جدا شده باشند.
- ثابتهای ریاضی: قوانین جهان تا چه اندازه دقیق هستند؟ طبق پیشنهاد برخی از دانشمندان، ما تنها جهان در بین جهانهای متعدد هستیم که اعداد درستی داریم.
- جهان قابل مشاهده: چه چیزی فراتر از لبه فضای قابلمشاهده قرار گرفته است؟ هیچکس به طور دقیق نمیداند و به احتمال زیاد هرگز کسی پاسخی به این سوال نداشته باشد. اما فکر اینکه جهان تا بینهایت گسترش یافته است بسیار هیجانانگیز است.
نظریه های مخالف چندجهانی
تعدادی از نظریهها، مخالف چندجهانی یا جهانهای موازی هستند. این نظریههای عبارنتد از:
- ابطالپذیری: هیچ راهی برای اثبات درستی یا نادرستی نظریههای چندجهانی وجود ندارد. هرگز فراتر از جهان قابلمشاهده را نخواهیم دید. بنابراین، اگر راهی برای رد کردن نظریهای وجود ندارد، آیا آن نظریه اعتباری خواهد داشت؟
- تیغ اوکام: گاهی، سادهترین ایدهها، بهترینها هستند. برخی از فیزیکدانها بر این عقیده هستند که نیازی به نظریه چندجهانی نیست. این نظریه نه تنها هیچ چالشی را حل نمیکند، بلکه چالشهای جدید را به وجود میآورد.
- عدم وجود مدرک: نه تنها نمیتوان نظریه چندجهانی را رد کرد، بلکه حتی قابل اثبات هم نیست. در حال حاضر هیچ مدرکی مبنی بر وجود جهانهای موازی نداریم.
کاربردهای فیزیک کوانتوم در زندگی
فیزیک کوانتوم یکی از بزرگترین موفقیتهای انسان امروزی است. اما دید بیشتر افراد به این شاخه از فیزیک با تردید بسیاری همراه است. هنگامی که نام فیزیک کوانتوم را میشنویم نخستین چیزی که به ذهنمان خطور میکند زنده یا مرده گربه شرودینگر است. یا حتی ممکن است به درهمتنیدگی کوانتومی فکر کنیم. فکر کردن به هر کدام از موضوعهای ذکر شده بسیار هیجانانگیز است، اما تحقیق در مورد آنها در آزمایشگاه نیازمند سیستمهای کوانتومی بسیار سادهای است. بنابراین، تصور کاربرد این پدیدهها در زندگی روزمره بسیار سخت خواهد بود.

جهان بر پایه فیزیک کوانتوم است. اما بسیاری از افراد این موضوع را نمیدانند. در ادامه، به تعدادی از کاربردهای فیزیک کوانتوم در زندگی روزمره اشاره میکنیم.
کاربرد فیزیک کوانتوم در توسترها
بیشتر افراد به هنگام صرف صبحانه و برای گرم کردن نان از توستر استفاده میکنند. در اینجا فیزیک کوانتوم آغاز میشود. اگر به داخل توستر داغ نگاه کنید، متوجه رنگ قرمز آن خواهید شد. توضیح آنکه چرا اجسام داغ با رنگ قرمز یا نزدیک به آن میدرخشند، نقطه شروع فیزیک کوانتوم بود.

رنگ نور تابیده شده توسط جسمی داغ مثالی از پدیدهای ساده و جهانی برای فیزیکدانهای نظری است. اینکه جسم از چه مادهای ساخته شده است مهم نیست. اگر آن را تا دمای مشخصی گرم کنیم و آسیبی نبیند،طیف نور تابیده شده توسط آن به طور دقیق مشابه هر ماده دیگری است. این حقیقت که نور مستقل از جنس ماده است ایده جهانی سادهای را بازگو میکند: همه رنگهای نور تابیده شده از جسمی را جمع میکنید و به هر کدام از آنها سهم مساوی از انرژی گرمایی داخل جسم میدهیم.
اما مشکلی که در اینجا وجود دارد آن است که تعداد راههایی که برای تابش نور با فرکانس بالا وجود دارند بسیار بیشتر از تابش نور با فرکانس پایین است. بنابراین، توستری که برای گرم کردن نان از آن استفاده میکنیم باید اشعههای گاما یا ایکس تابش کند. اما این اتفاق نمیافتد. در نتیجه، اتفاق دیگری باید بیافتد.
ماکس پلانک با ارائه فیزیک کوانتوم برای این مشکل راه حلی پیشنهاد کرد. بر طبق پیشنهاد او نور از بستههای انرژی به نام فوتون تشکیل شده است. بنابراین، نور تنها با انرژیهای مشخصی تابیده میشود. برای نور با فرکانس بالا، این انرژی کوانتومی بزرگتر از سهم انرژی گرمایی است که به آن فرکانس تخصیص داده شده است. در نتیجه، نور با فرکانس بالا تابیده نخواهند شد.
از این به بعد، هر زمانی که از توستر استفاده کنید به یاد خواهید آورد که اینجا نقطه شروع فیزیک کوانتوم است.
کاربرد فیزیک کوانتوم در چراغ های فلورسنت
به طور حتم یا از لامپهای فلورسنت استفاده کردهاید یا آنها را در مکانهای مختلف دیدهاید. رد پای فیزیک کوانتومی در این لامپها نیز مشاهده میشود.

در قرن ۱۹ میلادی، فیزیکدانها فهمیدند که هر عنصری در جدول تناوبی، طیف یکتایی دارد. اگر ساختار مادهای مشخص نباشد، با استفاده از خطوط طیفی میتوان عناصر تشکیل دهنده آن را مشخص کرد. حتی میتوان عناصر نامشخص را نیز شناخت.
اما توضیح این پدیده تا سال ۱۹۱۳ به تعویق افتاد. در آن سال، نیلز بور با استفاده از نظریه کوانتومی پلانک نخستین مدل کوانتومی را برای اتم ارائه داد. بر طبق پیشنهاد بور، الکترون در حالتهای فضایی معینی به دور هسته میچرخد. بنابراین، انرژی نور تابیده شده یا جذب شده توسط اتمها به فاصله این حالتها بستگی دارد. در نتیجه، برای هر اتمی فرکانسهای گسسته مشخصی وجود دارند.
از این ایده برای توضیح طیف نور تابیده شده توسط هیدروژن استفاده میشوند. با اینکه اتفاقی که داخل اتم میافتد با مدل ارائه شده توسط بور بسیار متفاوت است، اما اصل قضیه یکسان است. ایده اصلی پنهان شده در لامپهای فلورسنت همین مدل است. داخل هر لامپ فلورسنتی مقدار کمی بخار جیوه وجود دارد که به حالت پلاسما برانگیخته شده است. جیوه نوری با فرکانسهایی در محدوده نور مرئی تابش میکند.
اگر با استفاده از توری پراش ارزانی به لامپ فلورسنت نگاه کنید، تعداد کمی تصاویر رنگی مشخصی را خواهید دید. بنابراین، هر زمانی که از لامپهای فلورسنت در خانه یا محل کارتان استفاده کردید، از فیزیک کوانتوم تشکر کنید.
کاربرد فیزیک کوانتوم در کامپیوترها
با آنکه مدل بور بسیار مفید است، اما دلیل فیزیکی وجود حالتهای فضایی خاص برای الکترونها در ابتدا مشخص نبود. اما این دلیل در حدود ده سال قبل توسط لوییس دی بروگلی (Louis de Broglie) ارائه شد. بر طبق نظریه ارائه شده توسط دی بروگلی، ذراتی مانند الکترونها رفتار موجگونه خواهند داشت. اگر به الکترونها طول موجی وابسته به مقدار تکانه آنها نسبت دهیم، تعدادی مدارهای امواج ایستاده وجود دارند که موج الکترونی تعداد صحیحی از نوسانات به دور هسته را تشکیل خواهد کرد.
رفتار موجی الکترونها درک ما از چگونگی حرکت آنها در مواد را به طور اساسی تغییر داد. این تغییر اساسی سبب فهم بهتر ترازها و شکافهای انرژی داخل مواد شد. با استفاده از این شاخه از فیزیک مدرن خواص الکتریکی نیمهرساناها را کنترل میکنیم. به عنوان مثال، با تغییر مشخصات الکتریکی سیلیکون، ترانزیستور میسازیم.
بنابراین، هر زمانی که کامپیوتر یا لپتاپ خود را روشن میکنید، از رفتار موجی الکترونها استفاده کردهاید. در اینجا در مورد کامپیوترهای کوانتومی صحبت نکردیم، اما تمامی کامپیوترهای مدرن از فیزیک کوانتوم استفاده میکنند.

در صورت علاقهمندی به مطالعه بیشتر در مورد فیزیک کوانتوم، با مراجعه به مطلب «معرفی کتاب فیزیک کوانتوم — بهترین کتاب هایی که باید بخوانید» کتابهای مفیدی برای مطالعه خواهید یافت.
تاریخچه فیزیک کوانتوم
الکترون در حدود ۱۰۰ سال قبل و در سال ۱۸۹۷ توسسط جی جی تامسون (J. J. Thomson) کشف شد. اما دانشمندان سالها بعد و در سال ۱۹۳۲ به وجود نوترون پی بردند. اما آغاز نظریه کوانتوم به سال ۱۸۵۹ برمیگردد. در این سال، «گوتساو کیرشهوف» (Gutsav Kirchhoff) نظریه تابش جسم سیاه را ثابت کرد. بر طبق کشف این دانشمند، انرژی تابیده شده تنها به دما و فرکانس انرژی تابیده شده بستگی دارد. اما کیرشهوف معادلهای برای این رابطه ارائه نداد.
در سال ۱۸۷۹، «جوزف استفان» (Josef Stefan) بر طبق یافتههای آزمایشگاهی بیان کرد که انرژی تابیده شده از جسم سیاه متناسب با توان چهارم دما است. در سال ۱۸۸۴، بولتزمن (Ludwig Boltzmann) با استفاده از محاسبات نظری، ترمودینامیک و نظریه الکترومغناطیس ماکسول، به نتیجه یکسانی دست یافت. این نتیجه، اکنون به قانون استفان-بولتزمن معروف شده است. اما، این قانون به چالش کیرشهوف و به سوال مطرح شده در مورد طول موجهای خاص، پاسخی نداد.
در سال ۱۸۹۶، «ویلهلم وین» (Wilhelm Wien) راه حلی برای چالش وین ارائه داد. علیرغم آنکه راه حل ارائه شده توسط وین با مشاهدات تجربی برای مقدارهای کوچک طول موج همخوانی خوبی داشت، برای طول موجهای ناحیه فروسرخ با شکست مواجه شد. این مشکل توسط روبن و کرلبام مشاهد شد.
کیرشهوف از هایدنبرگ به برلین رفت. جایگاه کیرشهوف در ابتدا به بولتزمن و سپس به هرتز پیشنهاد شد، ولی آنها نپذیرفتند. اما در نهایت پلانک جایگزین مناسبی برای کیرشهوف شد. در اکتبر ۱۹۰۰ روبن به ملاقات پلانک رفت و نتایج به دست آمده را با او در میان گذاشت. هنوز زمان زیادی از رفتن روبن نگذشته بود که پلانک فرمول درست تابع کیرشهوف را حدس زد. حدس او با یافتههای تجربی در تمامی طول موجها همخوانی خوبی داشت. اما پلانک به دنبال به دست آوردن فرمول با استفاده از محاسبات نظری بود. برای این کار، او فرض کرد که انرژی گسسته است. بر طبق گفته پلانک تجربه ثابت خواهد کرد که آیا این فرضیه قابل درک توسط طبیعت است یا خیر.
پلانک از روش آماری بولتزمن برای اثبات فرمول استفاده کرد، اما رویکرد او به طور کامل متفاوت بود. فیزیکدان آلمانی ماکس پلانک نتیجه پژوهش خود در مورد اثر تابش ماده جسم سیاه را در سال ۱۹۰۰ چاپ کرد. همچنین، او برنده جایزه نوبل در سال ۱۹۱۸ شد.
در سال ۱۹۰۵ انیشتین اثر فوتوالکتریک را آزمایش کرد. به رها شدن الکترونها از فلزاتی مشخص یا نیمهرساناها پس از تابش نور، اثر فوتوالکتریک گفته میشود. نتایج به دست آمده بر پایه نظریه الکترومغناطیسی با شواهد تجربی همخوانی نداشتند. انیشتین به منظور حل این مشکل نظریه کوانتومی نور را پیشنهاد کرد. بعدها او نظریه پلانک در مورد رفتار کوانتومی نور را فهمید. یک سال بعد از آزمایش اثر فوتوالکتریک، انیشتین حدس زد که تغییرات انرژی ضریب صحیحی از است. او در سال ۱۹۲۱ جایزه نوبل فیزیک برای آزمایش فوتوالکتریک را دریافت کرد.
در سال ۱۹۱۳ نیلز بور مقالهای انقلابی در مورد اتم هیدروژن نوشت. او قوانین اصلی خطوط طیفی را کشف کرد. بور موفق به دریافت جایزه نوبل برای این کار در سال ۱۹۲۲ شد. آرتور کامپتون (Arthur Compton) در سال ۱۹۲۳ سینماتیک نسبیتی برای پراکندگی فوتون از الکترون ساکن را به دست آورد.
اما به نکته مهمی باید توجه کرد. ورود فیزیک کوانتوم به دنیای علم، مفاهیم جدیدی را به علم فیزیک اضافه کرد. ورود این مفاهیم به فیزیک منجر به نگرانی بسیاری از فیزیکدانهای مطرح شد. به عنوان مثال، نگرانی انیشتین در مورد وازه شانس بود. رادرفورد به هنگام بحث در مورد واپاشی رادیواکتیو در سال ۱۹۰۰ اثر خودبخودی را معرفی کرد.
در سال ۱۹۲۴، بور، کرامر و اسلاتر در مورد برهمکنش نور با ماده پیشنهادهای نظری ارائه کردند. اما این پیشنهادها منجر به رد فوتون شدند. گرچه این پیشنهادها اشتباه بودند اما کار تجربی مهمی را معرفی کردند. بور دو تناقض اصلی را در کار خود معرفی کرد:
- در حالیکه قسمتی از تغییرات انرژی پیوسته و قسمتی دیگر گسسته است، پایستگی انرژی چگونه برقرار است؟
- الکترون چگونه میداند که کی باید تابش کند؟
تناقض شماره ۲ سبب تحیر انیشتین شد. نظریه بور مورد قبول پائولی نبود.
در سال ۱۹۲۴ پژوهش بسیار مهم دیگری چاپ شد. این پژوهش توسط «ساتیندرا نس بوز» (Satyendra Nath Bose) انجام شده بود اما توسط داور مجله رد شد. بوز مقاله را برای انیشتین فرستاد و او بلافاصله ترتیب چاپ مقاله را داد. بوز حالتهای متفاوتی را برای فوتون پیشنهاد داد. همچنین بر طبق پیشنهاد او، هیچ پایستگی برای تعداد فوتونها وجود ندارد. بوز ذرات را در سلولهایی قرار داد و در مورد استقلال آماری سلولها صحبت کرد. با گذشت زمان، درستی نکات مطرح شده توسط بوز اثبات شدند.

در ادامه بروگلی در مورد دوگانگی رفتار ذرات در پایاننامه دکترای خود صحبت کرد و به الکترونها رفتار موجی نسبت داد. در سال ۱۹۲۶ شرودینگر مقالهای در مورد معادله اتم هیدروژن چاپ کرد. در این نقطه، مکانیک موجی متولد شد. شرودینگر برای هر متغیر دینامیکی، عملگری را معرفی کرد.
هایزنبرگ اولین مقاله خود در مورد مکانیک کوانتوم را در سال ۱۹۲۵ نوشت و دو سال بعد اصل عدم قطعیت را مطرح کرد. کار هایزنبرگ بر پایه روشهای ماتریسی است. در حقیقت، مکانیک ماتریسی هایزنبرگ و مکانیک موجی شرودینگر جایگاه ویژهای در علم فیزیک دارند.

در ابتدا اصل عدم قطعیت توسط کسی پذیرفته نشد. انیشتین یکی از اصلیترین مخالفان این اصل بود. او با نیلز بور در مورد این اصل ساعتها بحث کردند و در نهایت انیشتین مجبور به قبول این اصل شد. این تاریخچه کوتاه، راه بسیار طولانی فیزیک کوانتوم است. علمی که بسیاری از دیدگاهها را تغییر داد و دریچه جدیدی به روی فیزیکدانها باز کرد. جدول زیر خلاصه تاریخچه فیزیک کوانتوم را نشان میدهد:
| سال | کار انجام شده در زمینه فیزیک کوانتوم |
| ۱۸۶۴ | نظریه میدان الکترومغناطیسی |
| ۱۹۰۵ | نظریه نسبیت |
| ۱۹۰۵ | نظریه موج-ذره تابش الکترومغناطیسی |
| ۱۹۱۳ | نظریه اتمی |
| ۱۹۱۶ | نظریه کوانتمی نور |
| ۱۹۲۰ | نظریه جهش کوانتومی |
| ۱۹۲۰ | نظریه میدان کوانتومی |
| ۱۹۲۶ | نظریه کوانتومی جدید اتمها |
| ۱۹۵۰ | نظریه بسذرهای |
| ۱۹۵۲ | نظریههای متغیر پنهان |
| ۱۹۵۲ | نظریه موجی آزمایشی |
| ۱۹۵۷ | نظریه چندجهانی |
| ۱۹۶۲ | نظریه کوانتومی اثر رامان تحریکشده |
| ۱۹۶۸ | نظریه ریسمان |
| ۱۹۷۰ | نظریه Gauge |
| ۱۹۷۰ | نشریه مسیر کوانتومی |
| ۱۹۷۴ | نظریه میان کوانتومی شبکه |
| ۱۹۸۰ | نظریه پیچیدگی کوانتومی |
| ۱۹۸۰ | نتیجه حلقه کوانتومی |
| ۱۹۹۳ | نظریه جهان هولوگرافیک |
| ۲۰۱۳ | نظریه هولونومی کوانتومی |
اکنون میتوانید به پرسش فیزیک کوانتوم چیست پاسخ دهید. در ادامه به پرسشهای جالبی که در حوزه فیزیک کوانتوم مطرح شده است پاسخ میدهیم.
بزرگی ثابت پلانک چه مقدار است؟
اندازه ثابت پلانک بسیار کوچک و مقدار آن برابر است. همچنین کمیت دیگری به نام تعریف شده که مقدار آن برابر $$$$\frac{h}{2 \pi} = 1.054571726 \times 10^{-34} \ J.s = 6.58211928 \times 10^{-16} \ eV.s است. به عنوان مثالی در مورد استفاده از این ثابت، نور قرمز با طول موج ۵۰۰ نانومتر را در نظر بگیرید. فوتونی با نور قرمز دارای انرژی است.
اگر ثابت پلانک صفر بود، چه اتفاقی رخ میداد ؟
با قرار دادن ثابت پلانک برابر صفر به حد کلاسیکی فیزیک کوانتوم میرسیم. اگر این ثابت صفر یاشد، اصل عدم قطعیت از بین میرود، و در حالت حدی فیزیک کوانتوم شبیه مکانیک نیوتونی خواهد شد. همچنین، اگر h برابر صفر میبود جهان بسیار متفاوتتری نسبت به جهانی که میشناسیم داشتیم. زیرا، اجسام داغ تمام انرژی خود را به سرعت به صورت تابش الکترومغناطیسی فرکانس بالا (فاجعه فرابنفش) تابش میکردند. ماده بسیار سرد و نور بر سراسر جهان حاکم میبود.
درهم تنیدگی چیست؟
شرودینگر برای نخستین بار از این اصطلاح استفاده کرد. درهمتنیدگی به این معنا است که حالت کوانتومی یک ذره به جزییات حالت کوانتمی ذره دیگر بستگی دارد. درهمتنیدگی به طور معمول زمانی اتفاق میافتد که دو ذره درهمتنیده توسط منبع یکسانی تابش شدهاند. در این حالت، قانون پایستگی انرژی، تکانه یا تکانه زاویهای تنها زمانی برقرار است که مقدارهای مربوط به آن کمیت در ذرات همبستگی داشته باشند.
معرفی فیلم آموزش مکانیک کوانتومی ۱
مجموعه فرادرس در تولید و محتوای آموزشی خود اقدام به تهیه مجموعه فیلم آموزش فیزیک کوانتوم برای دانشجویان سال دوم و سوم کرده است:
در این مطلب، آموختیم که تناقض دیده شده بین نمودار تابش جسم سیاه و نظریه ارائه شده توسط دانشمندان آن زمان، آغازگر فیزیک کوانتوم بود. برای آشنایی بیشتر با این مبحث درس یکم این مجموعه آموزشی بسیار مفید خواهد بود. در درس یکم مبحث تابش جسم سیاه، مدلهای مشخصه در داخل یک کاواک، نظریه کوانتومی پلانک و نظریه کوانتومی ماده تدریس میشود. پس از دیدن درس یکم این فیلم آموزشی، درک عمیقتری از جسم سیاه و مفاهیم مرتبط با آن خواهید داشت.
مباحث مربوط به شکل نیوتنی مکانیک، معادلات لاگرانژ و دینامیک نسبیتی در درس دوم آموزش داده شده است. برای مقایسه فیزیک کلاسیک و فیزیک نیوتونی دیدن درس دوم توصیه میشود. در این مطلب از مجله فرادرس با صورت معادله موج شرودینگر در حالت کلی آشنا شدید. برای درک عمیقتر این معادله و حل آن برای سیستمهای خاص، تماشای درسهای سوم و چهارم توصیه میشود. در پایان، با مکانیک موجی در سهبعد و ذرات بدون برهمکنش، آشنا میشوید.
- برای دیدن فیلم آموزش مکانیک کوانتومی ۱ + اینجا کلیک کنید.
جمعبندی
در این مطلب از مجله فرادرس در مورد فیزیک کوانتوم صحبت کردیم. در ابتدا به پرسش فیزیک کوانتوم چیست پاسخ دادیم. در ادامه، در مورد موارد عجیب مطرح شده در مورد این شاخه از فیزیک صحبت کردیم. در پایان، تاریخچه کوتاهی در مورد پیدایش مکانیک کوانتوم و تلاشهای انجام شده در طی سالها برای گسترش آن بیان شد.
آزمون مطلب کوانتوم
۱. در فیزیک، واژه «کوانتوم» (Quantum) به چه معناست و چه کسی آن را برای اولین بار به کار برد؟
به کوچکترین واحد گسسته یک کمیت فیزیکی اشاره دارد و نخستینبار ماکس پلانک آن را استفاده کرد.
به پیوستگی حرکت ذرات اشاره دارد و اینشتین اولینبار واژه را مطرح نمود.
به موج بودن انرژی اشاره میکند و نخستینبار هایزنبرگ واژه را استفاده کرد.
به جفت ذره و پادذره مرتبط است و شرودینگر برای نخستین زمان آن را معرفی کرد.
واژه «کوانتوم» (Quantum) در فیزیک به کوچکترین مقدار گسسته هر مشخصه فیزیکی مانند انرژی اطلاق میشود. در این زمینه، ماکس پلانک اولین کسی بود که این واژه را در معنای علمی کنونی به کار گرفت.
۲. کدام ویژگی اساسی، رفتار ماده و انرژی را در فیزیک کوانتوم از فیزیک کلاسیک متمایز میکند؟
برخورداری ماده و انرژی از خاصیت موجی یا ذرهای به طور همزمان
انتقال انرژی به صورت پیوسته در تمام حالات
قابلیت پیشبینی دقیق آینده با دانستن شرایط اولیه
پذیرش اینکه سرعت و مکان یک ذره را میتوان همزمان با هر دقتی سنجید.
در فیزیک کوانتوم، رفتار ماده و انرژی به گونهای است که ذرات میتوانند همزمان خاصیت موجی و ذرهای از خود نشان دهند. این ویژگی با عنوان «دوگانگی موج/ذره» شناخته میشود و در فیزیک کلاسیک وجود ندارد. برخلاف گزینههایی مانند انتقال انرژی به صورت پیوسته یا قابلیت پیشبینی دقیق آینده، که مختص فیزیک کلاسیکاند، ویژگی دوگانگی موج/ذره منشا تمایز اصلی این دو حوزه است.
۳. اصل عدم قطعیت هایزنبرگ چه محدودیتی را بر اندازهگیری همزمان سرعت و مکان یک ذره ایجاد میکند؟
امکان مشخص کردن هر دو مقدار با دقت دلخواه وجود ندارد.
فقط موقعیت دقیق ذره بدون هیچ ابهامی قابل اندازهگیری است.
میتوان سرعت را بهطور کامل اما مکان را تقریبی سنجید.
هم سرعت و هم مکان همواره با دقت کامل قابل تعیین است.
طبق اصل عدم قطعیت هایزنبرگ، نمیتوان همزمان سرعت (تکانه) و مکان یک ذره را با دقت نامحدود دانست. هرچه یکی را با دقت بیشتری تعیین کنیم، از دقت دیگری کاسته میشود.
۴. دوگانگی موج/ذرهای نور و الکترون چیست و چرا برای فیزیک کوانتوم مهم است؟
دوگانگی موج/ذرهای یعنی نور و الکترون گاهی مانند موج و گاهی مانند ذره عمل میکنند که این ویژگی پایهای برای فیزیک کوانتوم است.
نور و الکترون همیشه فقط به صورت ذره رفتار میکنند و موج نیستند.
دوگانگی موج/ذرهای فقط در مورد امواج صوتی وجود دارد و به نور و الکترون مربوط نمیشود.
نور فقط موج است اما الکترون فقط ذره است و این تفاوت برای نظریه کوانتوم اهمیت دارد.
در فیزیک کوانتوم، مشخص شده که نور و الکترون بسته به شرایط میتوانند هر دو ویژگی موجی و ذرهای را نشان دهند. این رفتار باعث شد نظریههای قدیمی که فقط یکی را در نظر میگرفتند ناکافی باشد. اهمیت دوگانگی موج/ذرهای این است که بسیاری از پدیدههای کوانتومی، مانند پراش الکترون یا فوتوالکتریک، تنها با پذیرش این دیدگاه قابل توضیح هستند.
۵. در آزمایش دو شکاف یانگ، کدام تفاوت اصلی در رفتار موج و ذره هنگام عبور از شکافها قابل مشاهده است؟
ذرات و امواج فقط در نبود آشکارساز قابل شناسایی هستند و هیچ الگویی روی صفحه تشکیل نمیدهند.
امواج پس از عبور از شکافها الگوی تداخلی ایجاد میکنند، اما ذرات فقط از یک مسیر مشخص میگذرند.
امواج و ذرات هر دو پس از عبور از شکافها به صورت مستقیم و بدون تغییر حرکت میکنند.
ذرات در هر عبور همیشه از هر دو شکاف به صورت همزمان عبور میکنند، اما امواج فقط از یکی رد میشوند.
وقتی امواج مثل نور یا موج آب از دو شکاف یانگ عبور میکنند، در پشت شکافها الگوی تداخل شکل میگیرد که شامل نوارهای روشن و تاریک است. این الگو نتیجه همپوشانی دو موج و تقویت یا خنثی شدن آنهاست. اما ذرات مانند مهره یا تیله فقط از یکی از شکافها عبور میکنند و هر بار مسیر مستقلی دارند. در نتیجه کنار هم قرار گرفتن آنها هیچ نقش تداخلی مشاهده نمیشود. به همین دلیل، رفتار موجگونه باعث تداخل میشود، ولی ذره فقط از یک حفره عبور میکند و الگوی تداخل تشکیل نمیدهد.
۶. تابع موج ψ در معادله شرودینگر چه اطلاعاتی درباره ذره ارائه میکند؟
موقعیت دقیق ذره را در هر لحظه نشان میدهد.
احتمال حضور ذره در نقاط مختلف را تعیین میکند.
سرعت لحظهای ذره را به صورت مستقیم میدهد.
بار الکتریکی ذره را مشخص میکند.
تابع موج ψ در معادله شرودینگر اطلاعات احتمالاتی رفتار ذرات را ارائه میدهد. یعنی مقدار مربع این تابع، احتمال حضور ذره در نقاط گوناگون را تعیین میکند.
۷. اصل تطابق چه ارتباطی میان قوانین کلاسیک و قوانین کوانتومی برقرار میکند؟
قوانین کلاسیک فقط برای اتمهای رادیواکتیو معتبر است.
در شرایط خاص قوانین کوانتومی به قوانین کلاسیک تبدیل میشوند.
قوانین کوانتومی تنها در حضور میدان مغناطیسی به کار میروند.
همیشه قوانین کوانتومی و کلاسیک یکسان عمل میکنند.
اصل تطابق بیان میکند که در شرایط ویژه، قوانین کلاسیک را میتوان به صورت تقریبی از دل قوانین کوانتومی بهدست آورد. به این معنا که اگر متغیرها در مقیاس بزرگ یا شرایط خاصی قرار بگیرند، نتایج کوانتومی با نتایج مورد انتظار نظریه کلاسیک همخوان خواهد شد.
۸. فرمول که ماکس پلانک معرفی کرد، چه کاربرد یا نتیجهای در فیزیک داشت؟
تعیین چرایی دوگانگی موج/ذره در نور
توصیف فروپاشی تابع موج در آزمایش
اثبات وجود ذرات مجازی در خلا
حل مشکل فاجعه فرابنفش با فرض گسستگی انرژی
فرمول «حل مشکل فاجعه فرابنفش با فرض گسستگی انرژی» درست است زیرا پلانک با معرفی این فرمول نشان داد انرژی فقط در مقادیر گسسته جذب یا تابش میشود و این امر موجب شد توزیع انرژی تابش جسم سیاه به شکل صحیح و مطابق آزمایش پیشبینی گردد. در واقع، با این ایده، پیشبینیهای فیزیک کلاسیک (که شدت بینهایت برای امواج با فرکانس بالا انتظار داشت) اصلاح شد و فاجعه فرابنفش رفع گردید.
۹. اگر برهمنهی کوانتومی در عالم برقرار نبود، کدام رفتار متفاوت در ذرات رخ میداد؟
ذرات همزمان دارای ویژگیهای موجی و ذرهای بودند.
ذرات فقط در یک حالت یا موقعیت خاص وجود داشتند.
دقیقا نمیشد موقعیت و سرعت ذره را اندازه گرفت.
امکان پراش و تداخل امواج برای ذرات حذف میشد.
بر اساس مفهوم برهمنهی در مکانیک کوانتوم، ذره میتواند به طور همزمان در چند حالت یا موقعیت متفاوت وجود داشته باشد و تا زمان اندازهگیری این حالتها حفظ میشود. اگر برهمنهی وجود نداشت، ذره فقط در یک حالت یا موقعیت مشخص باقی میماند و امکان حضور همزمان در موقعیتهای مختلف از بین میرفت.
۱۰. در یک آزمایش کوانتومی، مشاهده پیوسته یک ماده باعث میشود واپاشی آن نسبت به حالت بدون مشاهده به تاخیر بیفتد یا متوقف شود. اهمیت این اثر در فهم کدام ویژگی اساسی فیزیک کوانتوم نهفته است؟
قابلیت انتقال انرژی گسسته بین حالات ماده
افزایش برهمنهی حالات کوانتومی ماده
اثر مشاهده بر رفتار سیستم و نقش مشاهدهکننده در نتایج
تاثیر بر مقدار ذرات مجازی در خلا
اثر زنو کوانتومی نشان میدهد مشاهده مکرر میتواند تحول یک سیستم کوانتومی را متوقف یا کند کند. اهمیت این پدیده در نمایش نقش موثر مشاهده و اندازهگیری بر رفتار سامانههای کوانتومی است. مشاهده مثل بخشی از خود فرآیند است و حالتی را تثبیت میکند. انتقال انرژی گسسته، ذرات مجازی و افزایش برهمنهی به طور مستقیم از این پدیده ناشی نمیشوند، بلکه تعامل مشاهدهگر با سیستم اهمیت دارد.
۱۱. پدیده تونلزنی کوانتومی چه نقشی در پایداری انرژی خورشید و ستارهها دارد؟
این پدیده باعث توزیع یکنواخت دما در کل ستاره میشود.
این پدیده منجر به آزاد شدن نور مرئی از سطح ستاره میشود.
تونلزنی انتقال گرما از هسته ستاره به سطح را ممکن میکند.
تونلزنی اجازه میدهد پروتونها سد دافعه را عبور کنند و همجوشی هستهای رخ دهد.
در مدل کوانتومی، تونلزنی باعث میشود پروتونها در هسته ستاره بتوانند علیرغم نیروی دافعه الکتریکی قوی، یکدیگر را پشت سر بگذارند و عمل همجوشی هستهای را انجام دهند. این فرآیند، کلید اصلی تولید انرژی خورشید و ستارههاست.
۱۲. در ستارههای کوتوله سفید، چه عاملی مانع فروپاشی گرانشی کامل آنها با وجود نیروی گرانش قوی میشود؟
تشکیل جفت ذره-پادذره نزدیک سطح کوتوله سفید
برهمنهی موجی/ذرهای حالت الکترونها
اصل طرد پائولی و ایجاد فشار تبهگنی
تابش پیاپی فوتونها توسط یونها
در کوتولههای سفید، پایه اصلی مقابله با فروپاشی گرانشی «اصل طرد پائولی و ایجاد فشار تبهگنی» است. این اصل بیان میکند که دو الکترون نمیتوانند همزمان در یک حالت کوانتومی قرار گیرند و همین موضوع باعث ایجاد فشاری کوانتومی به نام فشار تبهگنی میشود که جلوی فشرده شدن بیشتر ستاره را میگیرد.
۱۳. در فیزیک کوانتوم، برای شناسایی عناصر شیمیایی یک ستاره با استفاده از طیف نوری، چه روشی به کار میرود؟
بررسی تعداد کل رنگهای موجود در طیف و مقایسه با دادههای شناخته شده
تحلیل خطوط خاص جذب یا گسیل در طیف براساس ترازهای انرژی گسسته هر عنصر
بررسی تغییرات فرکانس طیف بر اثر حرکت ستاره نسبت به زمین
اندازهگیری شدت تابش کل ستاره و محاسبه دمای آن
در روش تحلیل طیف نوری، خطوط خاص جذب یا گسیل ظاهرشده بر اثر انتقال الکترونها میان ترازهای انرژی گسسته هر عنصر بررسی میشود. این خطوط برای هر عنصر منحصر به فردند و با مقایسه آنها با خطوط شناختهشده میتوان ترکیب شیمیایی ستاره را تعیین کرد. فقط با شناسایی این خطوط است که ساختار عناصر مشخص میشود.
۱۴. مدل Big Bang چگونه به کمک نوسانات کوانتومی اولیه شکلگیری ساختارهای بزرگ کیهانی را توضیح میدهد؟
نوسانات کوانتومی سرعت انبساط کیهان پس از Big Bang را کاهش دادند.
نوسانات کوانتومی باعث تفاوت جزئی در توزیع انرژی و ماده اولیه شدند.
نوسانات کوانتومی موجب فروپاشی سریع جهان در مراحل آغازین شدند.
نوسانات کوانتومی منجر به حذف کامل ماده در کیهان اولیه شدند.
مدل Big Bang با نظریه انبساط توضیح میدهد که نوسانات کوانتومی اولیه منجر به توزیع غیریکنواخت انرژی و ماده در جهان نوظهور شدند. همین تفاوتها به عنوان بذر اولیه برای شکلگیری ساختارهای بزرگ مثل کهکشانها عمل کردند.
۱۵. در آزمایش پراش الکترون، هنگام برخورد الکترون با آشکارساز چه نتیجهای درباره رفتار موجی-ذرهای ذره میتوان گرفت؟
الکترون مسیر موجی را کامل طی کرده و سپس ناپدید میشود.
الکترون همزمان در چند نقطه آشکارساز آشکار میشود.
الکترون مانند موج عبور میکند و انرژیاش بین نقاط متعدد پخش میشود.
الکترون فقط به عنوان ذره شناسایی میشود و موقعیت دقیقی دارد.
در آزمایش پراش الکترون، از الگوهای روی آشکارساز میتوان فهمید که الکترون در مسیر حرکتش مانند موج رفتار میکند و الگویی شبیه پراش نور تولید مینماید. اما زمانی که برخورد با آشکارساز رخ میدهد، الکترون تنها در یک نقطه مشخص ظاهر میشود. یعنی خصیصه ذرهای دارد و انرژی فقط در همان نقطه دیده میشود. عبارت «الکترون فقط به عنوان ذره شناسایی میشود و موقعیت دقیقی دارد» با نتیجه واقعی این آزمایش همخوان است
۱۶. اگر ثابت پلانک مقدارش صفر بود، چه تغییری در ویژگیهای اساسی جهان رخ میداد؟
همه مادهها به شکل امواج کاملا گسترده ظاهر میشدند و ذرهای وجود نداشت.
هیچ پدیده نوری در جهان دیده نمیشد و نور منتشر نمیگشت.
انرژی بین اجسام انتقال پیدا نمیکرد و هیچ حرکتی وجود نداشت.
تمام رفتارهای کوانتومی و احتمالها ناپدید میشد و جهان تنها قوانین کلاسیک داشت.
با صفر شدن ثابت پلانک، تمام ویژگیهای کوانتومی مثل گسستگی انرژی، دوگانگی موج/ذرهای و احتمالات از بین میرفت و همه چیز فقط با قوانین کلاسیک قابل توضیح بود. حتی در فیزیک کلاسیک انتقال انرژی و حرکت وجود دارد. همچنین حذف ثابت پلانک باعث حذف رفتار موجی هم میشود، نه موجیتر شدن جهان. پدیده نور در فیزیک کلاسیک هم قابل توصیف است.
۱۷. کدام ویژگی فیزیک کوانتوم زمینهساز ساخت فناوریهایی مانند ترانزیستور و لامپ فلورسنت شده است؟
تفسیر درهمتنیدگی کوانتومی و ارتباط ذرات
درک تابع موج و معادله شرودینگر در سطح اتمی
شناخت انرژیهای گسسته الکترون در مدلهای اتمی
توان پیشبینی چندجهانی و پیامدهای آن
عامل شکلگیری فناوریهایی مانند ترانزیستور و لامپ فلورسنت، شناخت ترازهای انرژی گسسته الکترون در مدلهای اتمی است زیرا رفتار ویژه انتقال و نشر انرژی توسط الکترونها پایه طراحی این ابزارها است.
۱۸. اصل عدم قطعیت هایزنبرگ چه نقشی در توضیح پدیده تابش هاوکینگ دارد؟
بیان میکند که سیاهچالهها فقط جرم بیشتری جذب میکنند و تبخیر نمیشوند.
تعیین میکند که فقط فوتونها میتوانند از سیاهچاله فرار کنند.
اجازه میدهد انرژی برای مدت کوتاهی وام گرفته شود و جفت ذره-پادذره ایجاد گردد.
اثبات میکند که ذرات مجازی تاثیری بر افق رویداد سیاهچاله ندارند.
در توضیح تابش هاوکینگ، اصل عدم قطعیت هایزنبرگ بیان میکند که در نزدیکی افق رویداد سیاهچاله امکان ظهور جفت ذره-پادذره به دلیل مجاز بودن «وام گرفتن» انرژی از طبیعت برای مدت بسیار کوتاه وجود دارد. یکی از این ذرات به سیاهچاله سقوط میکند و دیگری فرار میکند و این فرآیند به تدریج باعث تبخیر سیاهچاله میشود.













باسلام و احترام
جدول مقایسه فیزیک کلاسیک و کوانتوم ایراد دارد.
با سلام،
جدول مقایسه فیزیک کلاسیک و فیزیک کوانتوم بررسی و ایراد خاصی مشاهده نشد،
با تشکر از همراهی شما با مجله فرادرس
سلام وقتتون به کام.
یه سوالی داشتم خدمتتون
آیا اشتباهی در قیاس بین فیزیک کوانتوم و فیزیک کلاسیک رخ نداده؟
در اولین جدول این مقاله فرمودید که”فیزیک کلاسیک در مورد قوانین حاکم بر اجسام میکروسکوپی است.”
بعد در خانهی قبل هم باز فرمودید”فیزیک کلاسیک در مورد قوانین حاکم بر اجسام ماکروسکوپیک است” که بایستی چنین میبود که فیزیک کوانتوم در بررسی قوانین حاکم بر اجسام میکروسکوپی و فیزیک کلاسیک من باب قوانین حاکم بر اجسام ماکروسکوپیک صحبت میکند.
فکر کنم نیاز به یک ویرایش ساده باشه.
البته شاید هم بنده خطا میکنم ولی در کل گفتم اگر اشتباهی هست،لطف بفرمائید اصلاح کنید تا دوستان دچار سردرگمی نشن.
ضمنا مقاله بسیار مفید و جامع و با زبانی قابل فهم و درک بیان شده بود.
باتشکر و خسته نباشید🌹🫶🏻
سلام و وقت بخیر؛
متن بازبینی و اصلاح شد،
با تشکر از همراهی شما با مجله فرادرس
باسلام. البته نور به هنگام برخورد بامنشور بیشتر بازتابهای ذره ای دارد.که به نظرمن دلیل مجزا شدن رنگ ها میشود
در یک جمله به زبان ساده، فیزیک کوانتوم به چی میگن؟
فیزیک کوانتوم، مطالعه ماده و انرژی در سطوح زیراتمی و اتمی است که بعبارتی دیگر فیزیک را در مورد ذرات کوانتومی (اتمی و زیراتمی) با توجه به مکانیزم آنها اعمال میکند.
با سلام.
یه سوال خدمتتون داشتم.
این بود که انیشتین میگه هر جرم ساکنی دارای انرژی است؛و ما هم میتونیم بگیم که یک موج هم دارای انرژی هست.
با این اصل که گفتیم میتونیم بگیم <>؟
یعنی میتونیم با معادله E=mc²
بگیم ماده درحالتی انرژی دارد که موج هست؟و دلیلی هم بر موجی بودن نور هم باشه؟
عاشق فیزیک کوانتومی شدم😍
این مباحث تو رشته فیزیک هسته ای میاد؟
با سلام،
این مباحث در دوره کارشناسی و برای تمام گرایشهای فیزیک تدریس میشود،
با تشکر از همراهی شما با مجله فرادرس
با سلام،
توضیح داده شده صحیح نمیباشد.
با تشکر از همراهی شما با مجله فرادرس
با سلام و تشکر از از مطلب خوب شما.
لطفا میتونید بگید که با توجه به موجی بودن نور موقعی که با یک جسم برخورد میکند(صرف نظر از اینکه جسم بتواند نور برخورد شده را جذب کند)باید از جسم عبور کند؛
اما اگر ذرهای باشه (صرف نظر از شفاف بودن جسم) باید از جسم عبور نکند و بازتاب داده شود،
و بعد این میتونه یکی از دلایل دونگانگی موج و ذرهای نور باشه؟
با تشکر.
با سلام،
به این نکته دقت داشته باشید که رفتار موچی یا ذرهای نور متناسب با آزمایشی که انجام میشود در نظر گرفته خواهد شد. نور به هنگام برخورد به جسمی دلخواه رفتار موجی و در تابش جسم سیاه رفتار ذرهای دارد.
با تشکر از همراهی شما با مجله فرادرس