موج ایستاده — به زبان ساده

شاید تا به حال دیده باشید که وقتی یک طناب یا یک سیم را تکان میدهیم، ممکن است روی آن موجی ایجاد شود که فقط در آن مکان به طرف بالا و پایین نوسان کند، اما منتشر نشود. چنین موجی، موج ایستاده (Standing Wave) نامیده میشود. این امواج از برهمنهی دو موج رونده یا تعداد بیشتری از آنها تشکیل میشوند.
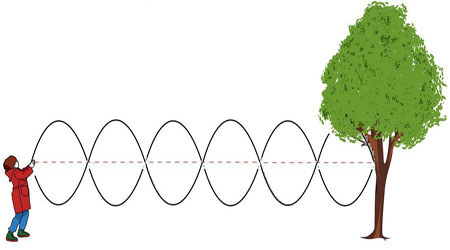
اگر دو موج با دامنه و طول موج یکسان در خلاف جهت هم حرکت کنند، برایند آنها شبیه موجی به نظر میرسد که در آن مکان متوقف شده است، از این رو، این موج را موج ایستاده مینامند.
دو موج با دامنه و طول موج یکسان را در نظر بگیرید که در خلاف جهت هم حرکت میکنند. معادله موج اول به صورت و معادله موج دوم به صورت هستند. اگر این امواج با هم تداخل یابند، موج برایند زیر را تشکیل خواهند داد:
با استفاده از اتحاد مثلثاتی میتوان این رابطه را ساده کرد. اگر و باشد، داریم:
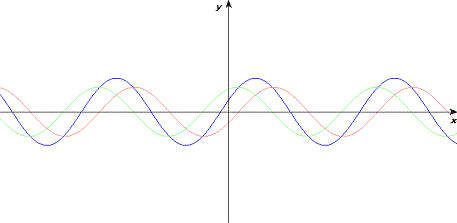
موج برایند حاصل، یک موج سینوسی (تابع مکان) است که در یک تابع کسینوسی (تابع زمان) ضرب شده است. در نمودارهای زیر، به صورت تابعی از در زمانهای مختلف رسم شده است که در آن، موج قرمز در جهت منفی محور و موج آبی در جهت مثبت محور حرکت میکند. موج سیاه نیز برهمنهی دو موج را نشان میدهد.
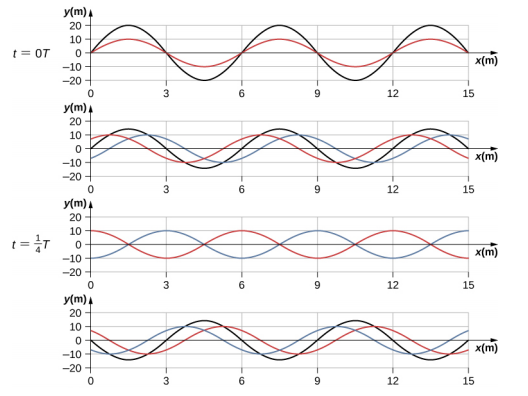
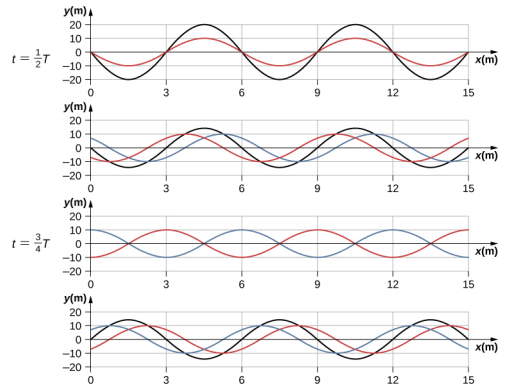
در زمانهای و ، دو موج همفازند و برایند آنها موجی است که دامنه آن دو برابر دامنه هر یک از امواج است. در واقع، این موجها در مضرب صحیحی از نصف دوره تناوب، همفاز هستند:
(همفاز، تداخل سازنده کامل)
در زمان های دیگر، دو موج، درجه ( رادیان) اختلاف فاز دارند و موج برایند آنها برابر با صفر است. این حالت در زمانهای زیر اتفاق میافتد:
(غیرهمفاز، تداخل ویرانگر کامل)
همانگونه که در نمودارها میبینیم، به ازای مقادیری از دامنه موج برایند همواره صفر است. این نقاط را «گره» (Node) مینامند. در واقع، در این نقاط موج برایند اصلاً حرکت نمیکند. برای به دست آوردن موقعیت گرهها، تابع سینوسی موج برایند () را برابر با صفر قرار میدهیم:
علاوه بر این، حالتهایی وجود دارد که دامنه موج برایند بیشینه است و بین نوسان میکند. این حالتها را پادگره (Antinode) یا شکم مینامند. موقعیت پادگرهها را میتوان به راحتی و با استفاده از به دست آورد:
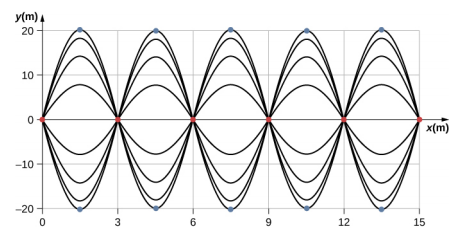
در شکل زیر، تصاویر لحظهای برایند دو موج یکسان که در خلاف جهت هم حرکت میکنند، نشان داده شده است. موج برایند، یک موج سینوسی است که در مضرب صحیحی از نصف طول موج گرهها ظاهر میشوند و پادگرهها نیز به دلیل جمله کسینوسی () بین نوسان میکنند. گرهها و پادگرهها به ترتیب با نقاط قرمز و آبی مشخص شدهاند.
موج ایستاده و تشدید
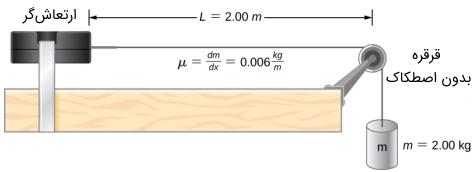
دستگاهی را در نظر بگیرید که در آن طنابی به یک ارتعاشگر وصل شده است و با فرکانس متغیر نوسان میکند. انتهای دیگر طناب که از روی یک قرقره بدون اصطکاک عبور میکند، به یک جسم معلق متصل است. مقدار نیروی کششی طناب برابر با وزن جسم آویختهشده است.
طناب دارای چگالی خطی ثابت (جرم بر طول) و تندی موج روی طناب برابر با است. شرایط مرزی متقارن (ایجاد گره در دو طرف طناب به دلیل ثابت بودن هر دو انتهای آن) موجب میشود تا طناب فقط با فرکانسهایی تشدید کند که منجر به تولید امواج ایستاده شود.
با شروع از فرکانس صفر و افزایش تدریجی آن، اولین مُد (Mode) به دست میآید. مد اول را مد اصلی یا هماهنگ اول (First Harmonic) مینامند. در این حالت، طول بین گرهها () برابر با نصف طول موج است؛ به عبارتی . بنابراین، فرکانس اصلی یا فرکانس هماهنگ اول برابر است با:
در اینجا تندی موج است. با ثابت نگه داشتن نیروی کششی و افزایش فرکانس میتوان هماهنگ دوم یا مد را به دست آورد. طول موج این مد و فرکانس آن دو برابر فرکانس اصلی است:
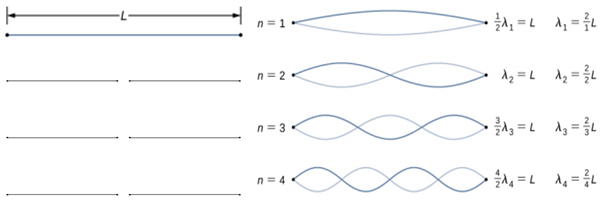
طول موجهای دو مد بعدی یعنی هماهنگهای سوم و چهارم به ترتیب و هستند که توسط فرکانسهای و به وجود میآیند. بنابراین، روابط طول موج و فرکانس هماهنگ اُم به صورت زیر خواهد بود:
این روابط برای هر موقعیت مرزی متقارن معتبر است. بنابراین، اگر در هر دو طرف پادگره داشته باشیم نیز این روابط برقرارند.
مثال ۱
طنابی به طول و چگالی جرمی خطی را در نظر بگیرید که به یک ارتعاشگر با فرکانس متغیر وصل شده است و انتهای دیگر آن از روی یک قرقره بدون اصطکاک عبور میکند. با استفاده از جسمی به جرم در طناب نیروی کششی ایجاد میشود.
(الف) سرعت امواج روی طناب چقدر است؟ (ب) سه مد نخست امواج تشکیل شده روی طناب را رسم کنید و طول موج آنها را بهدست آورید. (ج) فرکانسهایی که ارتعاشگر برای تولید سه مد نخست ایجاد میکند را محاسبه کنید.
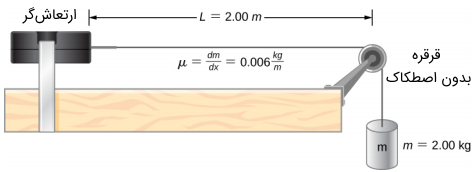
حل (الف): با استفاده از نیروی کششی و چگالی خطی طناب میتوان سرعت موج ایجاد شده را به دست آورد:
حل (ب): موقعیتهای مرزی به گونهای است که در دو انتهای طناب باید گره ایجاد شود. بنابراین، مد نخست برابر با نصف طول موج است. دو مد دیگر نیز با اضافه کردن نصف طول موج به دست میآیند:
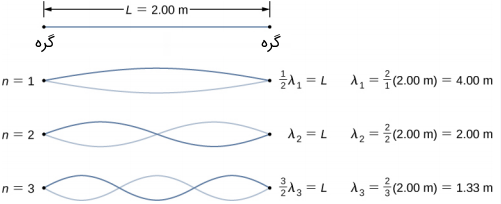
حل (ج): از آنجایی که سرعت موج برابر با طول موج در فرکانس است، فرکانس برابر با خواهد بود. بنابراین، داریم:
امواج ایستاده در لولههای صوتی باز و بسته
در شکل زیر امواج ایستاده تولیدشده در لولههای صوتی باز (دو انتها باز) نشان داده شده است (امواج را به صورت سهبعدی تجسم کنید).
در هر دو انتهای لوله باز، همانگونه که انتظار میرود، پادگره تشکیل میشود.
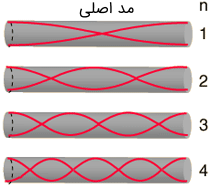
در این حالت، چون شرایط مرزی متقارن وجود دارد، روابط مربوط به طول موجها و فرکانسهای تشدید مانند روابط بهدست آمده برای طناب کشیده دو انتها ثابت است. بنابراین، اگر طول لوله برابر با باشد، خواهیم داشت:
که در آن، سرعت صوت است.
با استفاده از روش نمایش موج روی طناب، در شکل زیر امواج تولیدشده در لولههای بسته (یک انتها باز) رسم شده است (امواج را به صورت سهبعدی در نظر بگیرید). واضح است که در انتهای بسته، گره و در انتهای باز، پادگره تشکیل میشود. همانگونه که در شکل میبینیم، سادهترین موج ایستادهای که میتواند تحت این شرایط تشکیل شود، یکچهارم طول موج است. به عبارت دیگر، اگر طول لوله را برابر با در نظر بگیریم، خواهد بود. به همین ترتیب، برای هماهنگ دوم، سوم و چهارم، ، و طول موج را داریم.
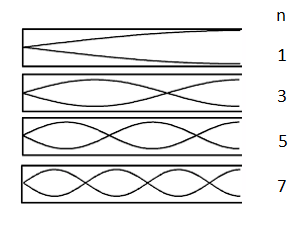
بنابراین، طول موج هماهنگ اُم برابر است با:
با استفاده از طول موج، به راحتی میتوان رابطه مربوط به فرکانسهای تشدید را به دست آورد:
پس در لولههای بسته فقط هماهنگهای فرد میتواند تولید شود.
مثال ۲
دو لوله صوتی بسته و به طول و را در نظر بگیرید. فرکانس کدام هماهنگ لوله با فرکانس هماهنگ سوم لوله برابر است؟
حل: با استفاده از رابطه فرکانس تشدید در لولههای بسته داریم:
لوله A:
لوله B:
با برابر قرار دادن این دو رابطه خواهیم داشت:
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
^^













برای من خیلی سخته متوجه نشدم ولی دوست دارم یاد بگیرم
سلام جناب حمیدی.
بابت این مطلب چطوری می توانیم صحبت کنیم؟ نیاز به مشاوره داریم.