حرکت براونی چیست؟ – از صفر تا صد
تصور کنید در اتاق تاریکی ایستادهاید و هوا درون اتاق به آرامی در جریان است. اگر به نور خورشید که از پنجره به داخل اتاق میتابد نگاه کنید متوجه حرکتهای تصادفی ذرات گرد و غبار در تمام جهتها خواهید شد. این حرکتهای تصادفی به دلیل برخوردهای پیوسته مولکولهای هوا با ذرات گرد و غبار است. در مثالی دیگر، دانههای گرده در آب پس از برخورد به یکدیگر به صورت تصادفی به اطراف پراکنده خواهند شد. این موارد، مثالهایی از حرکت تصادفی ذرات در محیط و از بارزترین مثالهای حرکت براونی در زندگی واقعی هستند.


حرکت براونی چیست ؟
به حرکت تصادفی ذرات غوطهور در شاره (مایع یا گاز) پس از برخورد با اتمها یا مولکولهای سریع، حرکت براونی یا حرکت کاتورهای گفته میشود. همچنین به مدلهای ریاضی که برای توصیف حرکتهای تصادفی ذرات استفاده میشوند نیز حرکت کاتورهای میگویند.
تاریخچه
حرکت براونی توسط زیستشناسی به نام «رابرت براون» (Robert Brown) در سال 1827 کشف شد. براون هنگامی که در حال مطالعه ذرات گرده غوطهور در آب توسط میکروسکوپ بود، متوجه حرکتهای لرزان ذرات کوچک در دانههای گرده شد. او ابتدا تصور کرد که گردهها زنده هستند. اما پس از تکرار آزمایش با ذرات گرد و غبار و مشاهده حرکتهای مشابه نتوانست توجیهی منطقی برای منشأ این حرکتها بیاید. ریاضیدان فرانسوی «لوییس بچلیر» (Louis Bachelier) نخستین کسی بود که توانست تئوری حرکت براونی را در پایاننامه دکترای خود ارائه دهد. در سال 1905 آلبرت انیشتین با استفاده از مدل احتمال توانست حرکت کاتورهای را به خوبی توضیح دهد.
به زبان ساده، دانههای گرده با مولکولهای آب برخورد میکنند. مولکولهای آب دیده نمیشوند ولی اثر برخورد آنها با دانههای گرده به صورت حرکتهای تصادفی به خوبی مشاهده میگردد. این اثر به حرکت براونی معروف است. این توضیح انیشتین در مورد حرکت براونی دلیل دیگری بر وجود اتمها و مولکولها است که به صورت تجربی توسط «جین پرین» (Jean Perrin) در سال 1908 اثبات شد.
جهت نیروی بمباران اتمی به طور پیوسته تغییر میکند و به ذره در زمانهای مختلف در یک جهت بیشتر از جهتهای دیگر ضربه زده میشود. این ضربهها سبب ایجاد حرکت تصادفی خواهد شد. در تصویر زیر حرکت کاتورهای را در یک و دوبعد مشاهده میکنید.

مقدمهای بر حرکت براونی
لاکپشتی را در نظر بگیرید که در اتاقی در حال حرکت است. از این لاکپشت به عنوان مدلی برای حرکت براونی استفاده خواهیم کرد.
در نتیجه، حرکت لاکپشت از مدل حرکت براونی پیروی خواهد کرد. اگر به لاکپشت اجازه دهیم آزادانه در اتاق حرکت کند آنگاه حرکت آن به صورت حرکت براونی در دوبعد خواهد بود که بسیار پیچیده است. بنابراین، لاکپشت را بین دو دیوار محصور میکنیم.
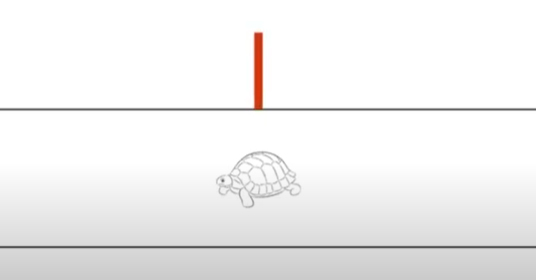
همانگونه که در تصویر بالا دیده میشود لاکپشت میتواند به راست یا چپ حرکت کند. نقطه آغاز حرکت لاکپشت را با قرار دادن خط قرمزی در تصویر مشخص میکنیم. در حرکت براونی، پس از گذشت زمان معین لاکپشت به سمت راست یا چپ حرکت خواهد کرد.
تصور کنید که اتاق را به مدت یک ساعت ترک میکنید. اکنون این سوال پیش میآید که پس از بازگشت به اتاق، لاکپشت در چه محلی قرار گرفته است. به دلیل آنکه حرکت لاکپشت کاملا تصادفی است و جهت حرکتش از یک زمان به زمان دیگر تغییر میکند پاسخ مشخصی برای این سوال وجود نخواهد داشت.
بهترین محلی که میتوان لاکپشت را در آنجا یافت کجا قرار دارد؟ پاسخ محل قرار گرفتن خط قرمز یعنی نقطه آغاز حرکت خواهد بود. اکنون تصور کنید که پس از گذشت زمان یک ساعت به اتاق برگشتهاید و لاکپشت را در سمت راست نقطه آغاز حرکت پیدا میکنید (خط سیاه).
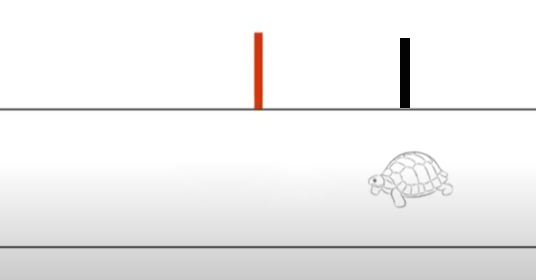
پس از یافتن لاکپشت در محل نشانهگذاری شده با خط سیاه، بار دیگر اتاق را ترک میکنید و پس از گذشت یک ساعت بازمیگردید. اکنون محتملترین مکانی که میتوانید لاکپشت را در آنجا پیدا کنید محل قرار گرفتن خط سیاه است (مکانی که لاکپشت را قبل از ترک اتاق در آنجا مشاهده کردید). در اینجا به نکته مهمی در حرکت براونی میرسیم. حتی اگر لاکپشت بار اول به سمت راست حرکت کند، احتمال اینکه حرکتی بعدی آن به سمت راست یا چپ باشد باز هم برابر خواهد بود.
با توجه به مثال بالا به این نتیجه میرسیم که در حرکت براونی حرکتهای گذشته تاثیری بر حرکتهای آینده نخواهند داشت.
مدل ساده ریاضی حرکت براونی
فرض کنید مکان لاکپشت در نقطه آغاز (خط قرمز) با نشان داده میشود. نخستین ویژگی حرکت براونی که در مثال حرکت لاکپشت دیدیم به صورت زیر بیان میشود.
رابطه ریاضی نوشته شده بدان معنا است که مکان مورد انتظار لاکپشت در زمان t برابر با مکان آن در زمان صفر است.
دومین ویژگی مهم حرکت براونی آن است که هر فاصله متوالی حرکت مستقل خواهد بود. در مثال لاکپشت اگر فاصله زمانی 0 تا ۱ ساعت و سپس ۱ تا ۲ ساعت را در نظر بگیرید هر رخدادی در یک بازه زمانی مستقل از دیگر بازههای زمانی خواهد بود.
دلیل رخ دادن حرکت براونی اعمال نیرو بر ذرات است. در فاصله زمانی بسیار کوتاهی نیروهای زیادی در جهتهای مختلف بر ذره وارد میشوند. جمع برداری نیروهای وارد شده جهت حرکت ذره را مشخص خواهد کرد. اگر نیروهای وارد شده بر ذره و فاصله زمانی در نظر گرفته شده بسیار کوچک شوند و به سمت صفر میل کنند آنگاه حرکت براونی مانند راه رفتنِ تصادفی خواهد شد.
رابطه زیر ویژگی اصلی آماری حرکت براونی را نشان میدهد.
در رابطه بالا $$overline{Z}(t)\$$
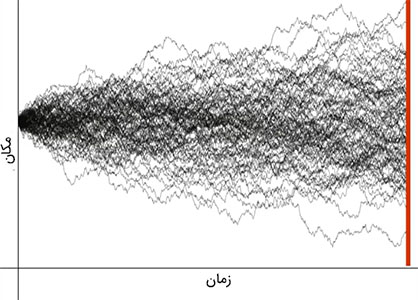
همانگونه که در تصویر مشاهده میکنید نقطه آغاز و نقطه پایان به طور متوسط یکسان هستند اما پراکندگی در اطراف نقطه پایانی بیشتر خواهد بود. همچنین با توجه به نمودار بالا میبینیم که با گذشت زمان، واریانس یا پراکندگی مکانی افزایش مییابد. در واقع این پراکندگی به طور خطی با گذشت زمان افزایش پیدا میکند.
رابطه خطی بین واریانس و زمان یکی از ویژگیهای آماری اصلی حرکت براونی است. با افزایش مقدار حرکت تصادفی دارای پراکندگی بیشتری در اطراف نقطه پایانی خواهد بود. در واقع با افزایش واریانس مقدار متوسط نقطه پایانی با نقطه آغاز یکسان است ولی مقدار پراکندگی در اطراف نقطه پایانی بیشتر میشود.
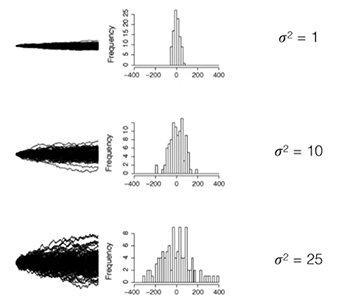
ویژگیهای حرکت براونی استاندارد
حرکت براونی استاندارد با نشان داده میشود که در آن t نشاندهنده زمان است. دو مشخصه اصلی حرکت براونی استاندارد عبارتند از:
۱. مقدار برابر صفر خواهد بود. در واقع مقدار حرکت براونی در زمان صفر برابر صفر است.
2. حرکت براونی دارای توزیع نرمال بر حسب میانگین صفر و واریانس t است. همچنین افزایش حرکت براونی () نیز دارای توزیع نرمال بر حسب میانگین صفر و واریانس t-s خواهد بود.
فرض کنید فردی در زمان صفر در مکان صفر قرار دارد. اکنون میخواهیم بدانیم مقدار حرکت براونی او در زمان t=2 چیست. همانگونه که در تصویر زیر دیده میشود حرکت براونی شخص میتواند مقادیر متفاوتی داشته باشد. نکته مهم آن است که بعد از گذشت 2 ثانیه با توجه به توزیع اندازه حرکت براونی میتوانیم مقدار مورد انتظار را بدانیم. با توجه به تابع توزیع رسم شده برای حرکت براونی در زمان ۲ ثانیه میتوان گفت که مقدار مورد انتظار حرکت براونی برابر صفر است ().
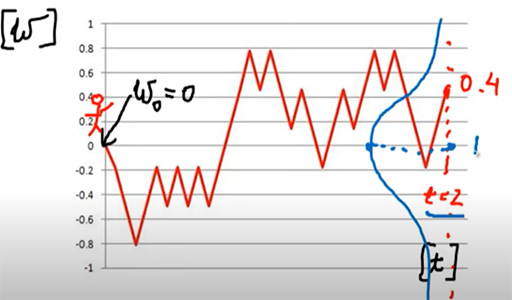
۳. در نمودار نشان داده شده اگر در هر فاصله زمانی به حرکت براونی نگاه کنیم، همیشه مقدار مورد انتظار صفر و واریانس تابعی از زمان خواهد بود. همچنین حرکت در یک فاصله زمانی، مستقل از حرکت در فاصله زمانی بعدی است و این دو هیچ تاثیری بر یکدیگر نخواهند داشت.
۴. «همپراشی» (covariance) دو مسیر حرکت براونی در زمانهای t و s برابر کمینه زمانهای مورد نظر خواهد بود.
۵. حرکت براونی «فرآیند مارکوف» (Markov Process) است. این عبارت بدان معنا است که کار انجام شده در آینده ربطی به گذشته نخواهد داشت. نیروهای تصادفی که ذره را پس از زمان حرکت میدهند مستقل از نیروهایی هستند که آن ذره را قبل از زمان حرکت دادهاند.
6. حرکت براونی یک «مارتینگل» (Martingle) است. در واقع انتظار داریم در زمان t در هر جایی ایستادهایم در زمان t+s نیز در همان نقطه باشیم.
7. حرکت براونی در همه جا پیوسته است و در هیچ نقطهای مشتقپذیر نیست.
8. حرکت براونی فراکتال است.
حرکت براونی و معادله نفوذ
مایعی را درون لوله یکبعدی در نظر بگیرید که با ذرات براونی پر شده است. اگر تعداد ذرات در مکان x و در زمان t باشد، تعداد ذرات در ناحیه کوچک dx به صورت خواهد بود.
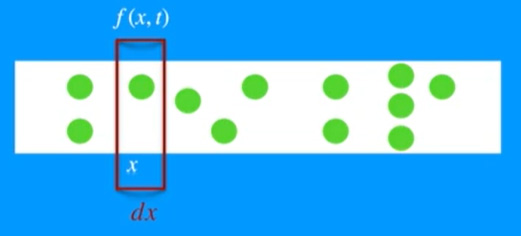
به دلیل آنکه ذرات در مایع دارای حرکت براونی هستند و به صورت پیوسته با مولکولهای مایع برخورد میکنند، در نتیجه با گذشت زمان تعداد ذرات در ناحیه مشخص شده تغییر خواهد کرد. اگر مایع مورد نظر، آب باشد با استفاده از عدد آووگادرو میدانیم که یک مول آب (۱8/015 گرم) شامل مولکول است. همچنین هر ذره براونی در هر ثانیه در حدود برخورد خواهد داشت. به دست آوردن معادله نفوذ برای چنین سیستمی بسیار مشکل است. انیشتین با سادهسازی سیستم فوق، معادله نفوذ را به دست آورد.
با فرض حرکت مستقل ذرات از یکدیگر، پس از گذشت زمان تابع توزیع ذرات به صورت زیر نوشته خواهد شد.
همانگونه که در تصویر زیر مشاهده میکنید ناحیه دیگری به فاصله از ناحیه اول نشان داده شده است. تعداد ذرات در این ناحیه با بیان خواهد شد.
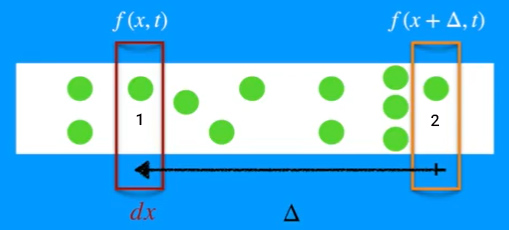
اگر تابع احتمال جابجایی با نشان داده شود آنگاه تعداد ذراتی که در ناحیه ۲ قرار دارند به صورت زیر نوشته خواهد شد.
اکنون اگر از ناحیه ۲ به اندازه در امتداد محور افقی حرکت کنیم تعداد ذرات به صورت زیر بیان خواهد شد.
از آنجایی که ذرات داخل مایع با احتمال یکسانی به سمت چپ یا راست حرکت میکنند در نتیجه دو تابع احتمال با یکدیگر برابر خواهند بود.
تعداد ذرات پس از گذشت زمان به صورت زیر نوشته میشود.
با حذف dx از طرفین معادله داریم.
با استفاده از بسط تیلور تابع به صورت زیر نوشته خواهد شد.
به دلیل کوچک بودن از توانهای بالاتر آن صرف نظر شده است. همچنین تابع نیز با استفاده از بسط تیلور به صورت زیر نوشته میشود.
با جایگزینی دو رابطه به دست آمده برای تابعهای و در رابطه (۱) خواهیم داشت.
از آنجایی که تابع با با یکدیگر برابر هستند در نتیجه عبارت برابر با صفر خواهد بود. همچنین، میدانیم جمع کل احتمال برابر یک میشود در نتیجه داریم.
بنابراین، رابطه (۲) به صورت زیر خلاصه میشود.
با تعریف معادله نفوذ به صورت زیر به دست خواهد آمد.
هر چه مقدار D بزرگتر باشد، ذرات براونی با سرعت بیشتری حرکت خواهند کرد. همچنین ضریب نفوذ به سه عامل زیر بستگی خواهد داشت.
- دما
- اندازه ذرات
- ویژگیهای مایعی که ذرات براونی در آن قرار گرفتهاند.
با جایگزینی رابطه (۳) با تقریب دیفرانسیلی داریم.
با توجه به رابطه بالا به دو نتیجه میرسیم.
- قسمت چپ معادله بیانگر تغییرات تعداد ذرات در مکان x نسبت به زمان است.
- قسمت راست معادله بیانگر آن است که میانگین تعداد ذرات در اطراف ناحیه x نسبت به تعداد ذرات در ناحیه x بیشتر خواهد بود.
در صورتی که N ذره در مکان و زمان صفر شروع به حرکت کنند، معادله نفوذ دارای جواب زیر خواهد بود.
معرفی فیلم آموزش مبانی مکانیک آماری پیشرفته ۱
به منظور درک بهتر فیزیک آماری حاکم بر حرکت براونی مجموعه فرادرس در تهیه و تولید محتوای آموزشی خود اقدام به تهیه فیلم آموزش مبانی مکانیک آماری پیشرفته ۱ برای دانشجویان رشته فیزیک کرده که این مجموعه آموزشی از هشت درس تشکیل شده است.
درس یکم در در مورد مبانی ترمودینامیک و آشنایی با حالتهای میکروسکوپیک و ماکروسکوپیک است. در درسهای دوم تا چهارم با مبانی نظریه آنسامبل و حالتهای کوانتومی و فضای فاز آشنا خواهید شد. مقدمات ریاضی حرکت براونی را در درس پنجم فرا خواهید گرفت. در این درس تغییرات زمانی ضرایب تابع احتمال و محاسبه مقدار انتظاری را فرا خواهید گرفت.
- برای دیدن فیلم آموزش مبانی مکانیک آماری پیشرفته ۱ + اینجا کلیک کنید.
کاربرد های حرکت براونی در زندگی روزمره
ذراتی که تحت تاثیر حرکت براونی قرار میگیرند مسیر زیگزاگ مانندی را طی خواهند کرد. اندازه ذرات با سرعت آنها رابطه معکوس دارد. این بدان معنا است که ذرات کوچکتر نسبت به ذراتی با اندازه بزرگتر، سریعتر حرکت خواهند کرد. همچنین، انتقال تکانه با جرم ذرات رابطه معکوس دارد. بنابراین، ذرات کوچکتر پس از برخورد انرژی بیشتری را به دست خواهند آورد و سریعتر حرکت میکنند. ویسکوزیته شاره عامل دیگری است که بر حرکت براونی ذره تاثیر میگذارد. ذرات در محیطی با ویسکوزیته کمتر، سریعتر حرکت خواهند کرد.
پس از آشنایی با مفهوم حرکت براونی و به دست آوردن معادله نفوذ، در ادامه به کاربردهایی از این مفهوم در زندگی روزمره میپردازیم.
حرکت دانههای گرده در آب راکد
دانههای گرده در آب به صورت تصادفی به یکدیگر برخورد میکنند بنابراین دارای حرکت براونی خواهند بود. برخورد ذرات با یکدیگر سبب تغییر بزرگی در تکانه میشود. این تغییر بر سرعت حرکت ذرات تاثیر میگذارد.

حرکت ذرات گرد و غبار در اتاق
حرکت ذرات گرد و غبار در حالت عادی قابل رویت نیست اما به کمک اثر تیندال، حرکات تصادفی این ذرات به آسانی مشاهده میشود. این حرکتهای تصادفی ذرات مثال واضحی از حرکت براونی در زندگی روزمره است.
مولکولهای آب
از آنجایی که مولکولهای آب هنگام حرکت از الگوی مشخصی پیروی نمیکنند حرکتهای آنها قابل پیشبینی نیست. این حرکتهای تصادفی مولکولهای آب مثال دیگری از حرکت براونی است. سرعت حرکت مولکولهای آب با افزایش دما بیشتر میشود.
نفوذ کلسیم به استخوان
نفوذ هنگامی رخ میدهد که ماده از ناحیهای با غلظت بالا به ناحیهای با غلظت کم حرکت کند. نفوذ کلسیم از میان استخوانها یکی از بهترین مثالهای حرکت براونی در زندگی روزمره است. جذب کلسیم توسط استخوانها به کمک نفوذ انجام میشود.
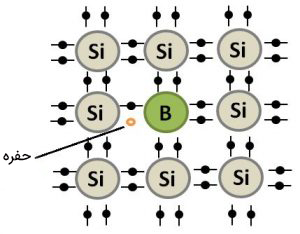
حرکت حفرههای بار الکتریکی در نیمهرساناها
هنگامی که الکترون از نوار ظرفیت به نوار رسانش میرود، حفرهای در نوار ظرفیت ایجاد خواهد شد. حرکتهای کاملا تصادفی الکترونها و حفرهها داخل نیمهرساناها نشاندهنده حرکت براونی است.
نفوذ آلایندهها در هوا
آلایندهها، مولکولهای گاز، ذرات گرد و غبار و دیگر ذرات موجود در هوا حرکت براونی را به بهترین صورت نشان میدهند. در این حالت، هوا مانند یک شاره رفتار میکند و ذرات متحرک پس از برخوردهای پیوسته به یکدیگر انرژی منتقل میکنند.
ذرات پلاسما در سلول
ذرات پلاسما در سلول تعدادی واکنشهای شیمیایی را مانند برخورد بین ذرات باردار و خنثی، برخورد کشسان، برخورد غیرکشسان و برخورد الکترون با یون انجام میدهند. این برخورد ذرات با یکدیگر سبب انتقال انرژی و تغییر در مقدار تکانه خواهد شد.
حرکت الکترونها در رسانا
حرکت الکترونها در رسانا نیز مثال دیگری از حرکت براونی است.












