بسط تیلور — به زبان ساده

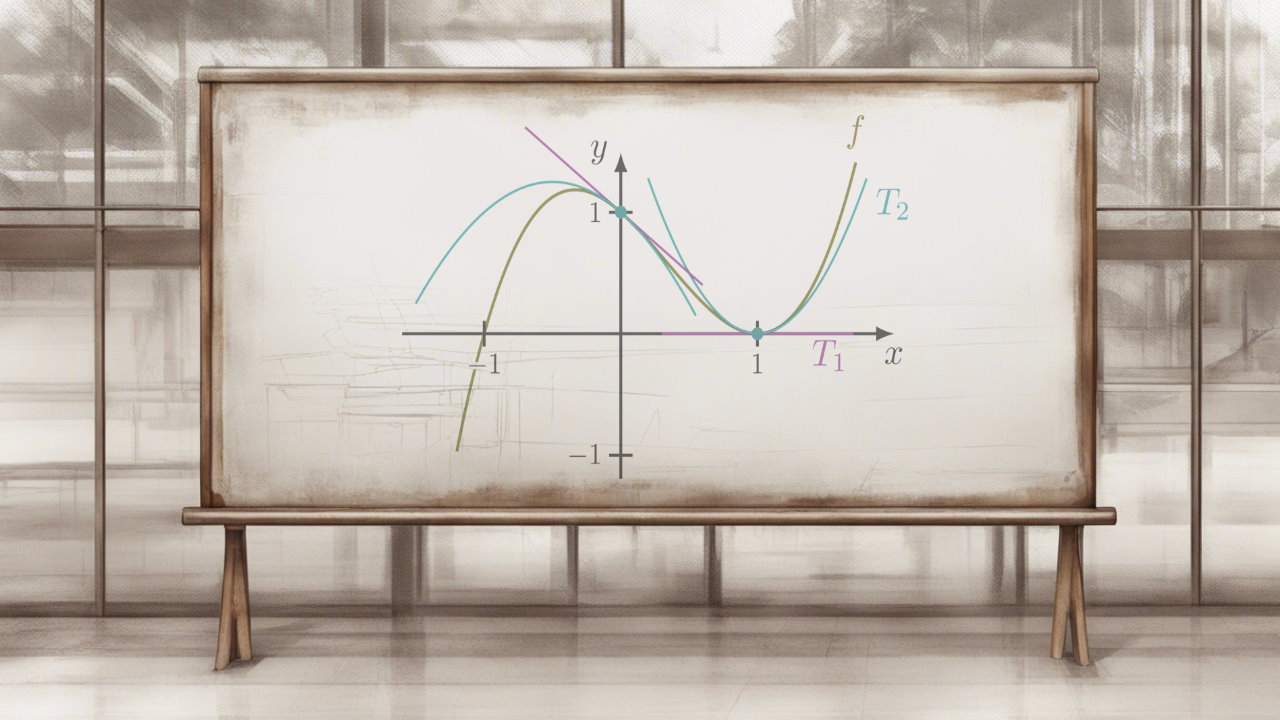
شاید تاکنون بارها با عبارت بسط مواجه شده‌اید، ولی معنی دقیق آن را نمی‌دانید. مثلاً ممکن است با عباراتی چون بسط دوجمله‌ای، بسط نیوتن، بسط لاپلاس و یا بسط تیلور مواجه شده باشید. در ریاضیات بسط به معنی روش متفاوتی برای نمایش یک عبارت یا رابطه ریاضی است. در مورد بسط تیلور یک تابع به صورت مجموع بی‌نهایت جمله به نمایش در‌می‌آید که از مشتق‌های تابع در یک نقطه به دست می‌آید. ریاضیدان انگلیسی، بروک تیلور، در سال ۱۷۱۵ میلادی، مفهوم سری تیلور را به‌طور رسمی معرفی کرد.در جدول زیر نمونه‌هایی از این بسط‌ها برای عبارات مختلف ارائه شده‌اند:

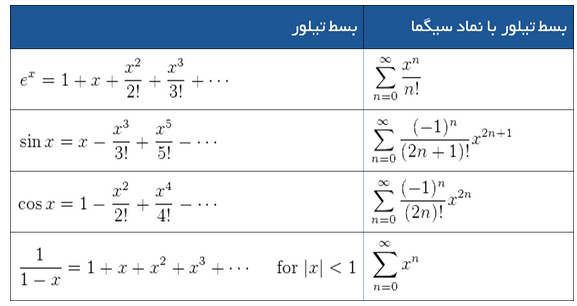
توجه کنید که بسط‌های تبلور محدود به موارد فوق نیستند.

توجه: نسخه کامل‌تری از این مطلب در مجله فرادرس تهیه و منتشر شده است که می‌توانید با مراجعه به این لینک آن را مطالعه کنید.

تقریب

شما می توانید با استفاده از چند چند جمله اول یک بسط تیلور، مقدار تقریبی یک تابع را به دست آورید. در اینجا ما تقریب‌های تابع (cos(x را نشان می‌دهیم که رفته‌رفته دقیق‌تر می‌شوند. خط قرمز، نمودار تابع (cos(x و خط آبی تقریب ما در هر مرحله است:

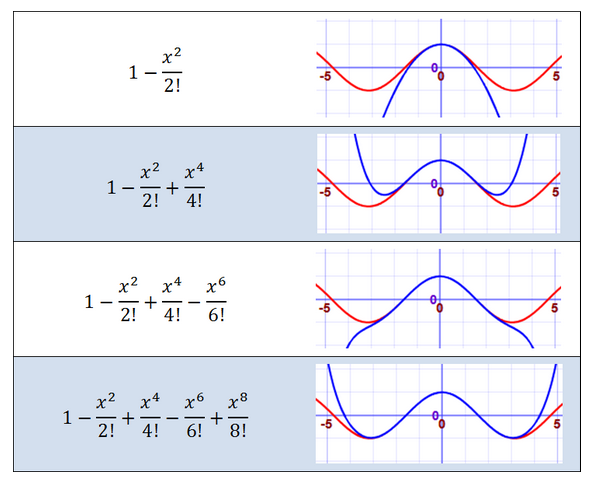
همچنین می‌توان کاربرد سری‌های تیلور را در فرمول‌های اوبلر مشاهده کرد.

این چه نوع جادویی است؟

شاید از خود بپرسید چگونه یک تابع به سری جملات بزرگ مانند این تبدیل می شود؟ در واقع این جادو نیست. ابتدا در نظر داشته باشید که می‌خواهیم عبارت زیر را به دست آوریم:

f(x) = c₀ + c₁(x-a) + c₂(x-a)² + c₃(x-a)³ + …

سپس مقداری مانند a را در نظر می‌گیریم و مقادیر c₀ و c₁ و c₂ و … را به دست می‌آوریم. به دست آوردن اعداد ذکر شده با استفاده از مشتق‌ها ممکن است. اگر در مورد مفهوم مشتق ابهام دارید باید بیان کنیم که یک مشتق، شیب یک تابع را در هر نقطه نشان می‌دهد. باید مشتق های تابع (f(x و قوانین مشتق ساده زیر را بدانید:

• مشتق هر عدد ثابت برابر 0 است.
  مشتق x، برابر 1 است.
  مشتق عبارت xn، برابر nxn-1 است. مثال: مشتق x3 برابر 3×2 است.

اینک ‌می توانیم محاسبه خود را شروع کنیم:

• برای یافتن c0، همان طور که گفته شد، مقدار x را برابر a در نظر می‌گیریم، پس تمامی عبارات (x – a) برابر صفر می‌شود  و عبارت زیر برای شما باقی می‌ماند:

f(a) = c₀
پس c₀ = f(a)

برای بدست آوردن c₁، مشتق (f(x را به دست می‌آوریم.

f ’(x) = c₁ + 2c₂(x – a) + 3c₃(x – a)² + …

چون x=a، پس عبارات (x – a) برابر صفر می‌شود:

f ’(a) = c₁
پس c₁ = f’(a)

برای به دست آوردن c₂، دوباره مشتق‌گیری می‌کنیم:

f ’’(x) = 2c₂ + 3 × 2 × c₃(x – a) + …

چون x=a، پس عبارات (x – a) برابر صفر می‌شود:

f ’’(a) = 2c₂

پس c₂ = f ’’(a)/2

در واقع، یک الگو به دست می‌آید. هر جمله برابر است با:

• مشتق عبارت قبلی …
• … تقسیم بر تمامی توان‌هایی که تا اینجا ضرب شده‌اند، که برای آن می‌توانیم از نماد فاکتوریل استفاده کنیم. برای مثال:

3! = 3 × 2 × 1 ).

و عبارت زیر به دست می‌آید:

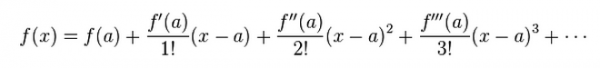
اکنون ما روشی برای یافتن سری تیلور خود داریم. کافی است مشتق‌گیری را ادامه دهید و در هر مرحله بر !n تقسیم کنید.

مثال: سری تیلور برای (cos(x

تمام اطلاعات اولیه ما به شرح زیر است:

• مشتق (cos(x برابر(sin(x- است.
• مشتق (sin(x برابر (cos(x است.

a را برابر صفر قرار می‌دهیم:

• c₀ = f(0) = cos(0) = 1
• c₁ = f'(0)/1! = -sin(0) = 0
• c₂ = f'(0)/2! = -cos(0)/2! = -1/2!
• c₃ = f'(0)/3! = sin(0)/3! = 0
• c₄ = f'(0)/4! = cos(0)/4! = 1/4!
•  و …

جملات فرد همگی برابر صفر هستند. پس عبارت زیر به دست می‌آید:

cos(x) = 1 − x²/2! + x⁴/4! − …

این عمل را خودتان برای تابع (sin(x امتحان کنید تا موضوع را به خوبی متوجه شوید.
یا می‌توانید این عمل را به دلخواه روی تابعی دیگر امتحان کنید. مسئله کلیدی این است که شما باید قادر باشید که از تابع (f(x خود مشتق‌گیری کنید.

نکته: سری (بسط) مک لورن (Maclaurin Series)، همان سری تیلور است که در آن a = 0 است. پس تمامی مثال‌هایی که استفاده کردیم، می‌توانند بسط یا سری مک لورن نام بگیرند.

اگر این نوشته مورد توجه شما قرار گرفته است، احتمالاً موارد زیر نیز برای شما جالب خواهند بود:

• آموزش قضیه بسط دو جمله ای و مثلث خیام
• آموزش نرم افزار متمتیکا (Mathematica) برای حل معادلات ریاضی
• لگاریتم – معرفی مفاهیم پایه به زبان ساده
• آموزش معادلات اویلر و نقاط تکین (منفرد) منظم
• آموزش روش های حل روابط بازگشتی

==