رگرسیون خطی با متغیرهای طبقه ای در SPSS — راهنمای گام به گام

در روشهای رگرسیون خطی، معمولا فرض بر این است که متغیرهای توصیفی یا مستقل، کمی هستند. ولی گاهی پیش میآید که بخواهیم رابطه بین یک متغیر وابسته را با یک یا چند متغیر مستقل که ممکن است بعضی از آن ها کیفی باشند، تحلیل کنیم. در چنین حالتی باید محاسبات مربوط به برآورد مدل و تعریف متغیرهای مستقل را با احتیاط انجام داد. در این مطلب به بررسی مدلهای رگرسیون خطی با متغیرهای مستقل طبقهای میپردازیم.
باید توجه داشت که مقدارهای مربوط به این متغیرهای کیفی براساس ماهیتشان با کدگذاری به عدد تبدیل شدهاند. برای مثال متغیرهای کیفی با مقیاس ترتیبی (Ordinal) دارای کدهای عددی هستند که ترتیب را نشان دهد و متغیرهای کیفی اسمی (Nominal) براساس کدگذاری که فقط تفکیک را نشان دهند تبدیل به عدد شدهاند. در این مطلب منظور از متغیرهای کیفی همان «متغیرهای طبقهای» (Categorical) است که با هدف تفکیک یا دستهبندی اعضای جامعه به کار میروند.
پیشنهاد میشود برای آشنایی بیشتر با نحوه کدگذاری متغیرهای کیفی مطلب جامعه آماری — انواع داده و مقیاسهای آنها و به منظور آمادگی برای درک مفاهیم رگرسیون خطی، رگرسیون خطی — مفهوم و محاسبات به زبان ساده را مطالعه کنید.
رگرسیون خطی با متغیرهای مستقل طبقهای
بهتر است ابتدا با یک مثال شروع کنیم. فرض کنید میخواهیم رابطه جنسیت سرپرست خانوار را با هزینه خانوار مورد بررسی قرار دهیم. واضح است که متغیر جنسیت سرپرست خانوار یک متغیر طبقهای است که میتواند دارای کد گذاری ۰ و ۱ باشد. در این حالت به نظر میرسد که متغیر مستقل در اینجا جنسیت و متغیر وابسته نیز هزینه است.
پس اگر متغیر مستقل جنسیت با و همچنین متغیر هزینه خانوار (وابسته) را با Y نشان دهیم، مدل رگرسیونی میتواند به صورت زیر باشد:
همانطور که مشخص است مقدار ثابت و ضریب متغیر مستقل هستند. جمله خطا نیز با e نشان داده شده است. میدانیم متغیر مستقل که معرف جنسیت سرپرست خانوار است، دارای دو طبقه زن و مرد است. این طبقات باید در مدل رگرسیونی با دو مقدار ۰ و ۱ مشخص شوند. برای مثال اگر سرپرست خانوار زن باشد مقدار متغیر برابر ۰ و در صورتی که سرپرست مرد باشد، ۱ خواهد بود. بنابراین میتوان مدل را برحسب گروه سرپرست خانوار به دو صورت تفکیک کرد. اگر سرپرست زن باشد مدل به صورت و در صورتی که سرپرست مرد باشد مدل به شکل در میآید. اگر مقدار را با جمع کنیم، مدلی که برای سرپرست خانوارد مرد نوشته میشود به صورت زیر در میآید.
و برای سرپرست زن نیز مدل رابطه بین درآمد و هزینه خانوار به صورت زیر است:
همانطور که دیده میشود، در گرسیون خطی، وجود متغیر مستقل طبقهای که دارای دو مقدار یا دو طبقه (Category) باشد، فقط در میانگین مدل تاثیر میگذارد. در این حالت مشخص است که برآورد ، میانگین هزینههای خانوار با سرپرست زن و میانگین هزینههای خانوار با سرپرست مرد است. در نتیجه تفاضل بین این دو میانگین میتواند برآورد باشد.
مثال ۱
اطلاعات مربوط به هزینه 18 خانوار به تفکیک جنسیت سرپرستشان در جدول زیر قرار دارد. مدل مناسب رگرسیونی را با توجه به توضیحات بالا برای این متغیرها مییابیم. برای انجام محاسبات از نرمافزار SPSS کمک میگیریم.
| سرپرست | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| هزینه | 115 | 120 | 121 | 144 | 140 | 150 | 160 | 132 | 144 |
| سرپرست | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| هزینه | 210 | 220 | 200 | 220 | 230 | 170 | 188 | 165 | 120 |
برای اجرای رگرسیون خطی از فهرست Analysis گزینه Regression و دستور Linear را انتخاب و در پنجره مربوطه تنظیمات را مطابق تصویر زیر انجام میدهیم. واضح است که متغیر X را سرپرست و Y را هزینه در نظر گرفتهایم.
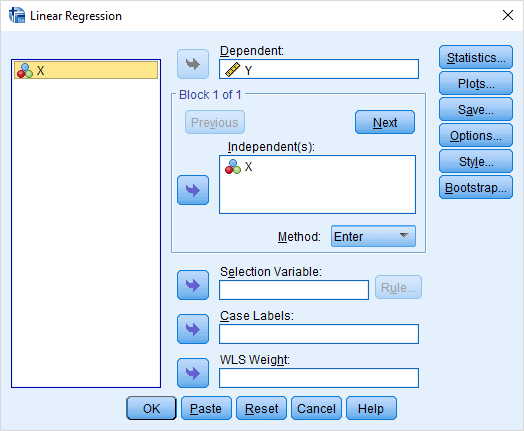
با اجرای این دستور خروجی و محاسبات مربوط به برآورد پارامترهای مدل، توسط SPSS انجام میشود. تصویر زیر این خروجی را نمایش میدهد. ضریب همبستگی (R) و همچنین R-Square وجود رابطه بین متغیر مستقل و وابسته را تایید میکنند.
در جدول مربوط به Coefficients پارامترهای مدل را میبینید. مشخص است که مقدار و برآورد پارامترها است. مقدار احتمال (Sig) برای هر دو پارامتر نیز از احتمال خطای نوع اول که در اینجا آن را برابر با 0.05 در نظر میگیریم کمتر است. این موضوع نیز تاییدی بر مناسب بودن مدل و رابطه ایجاد شده است.
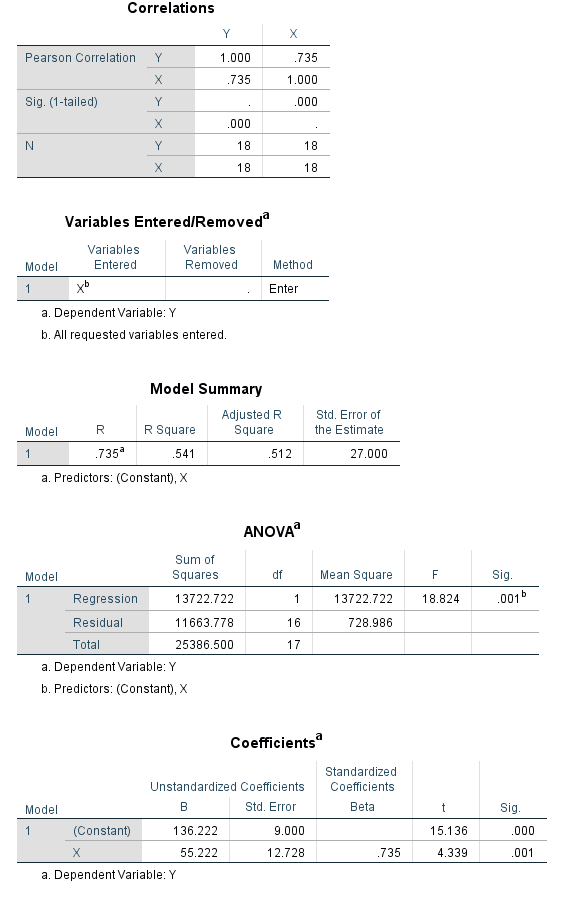
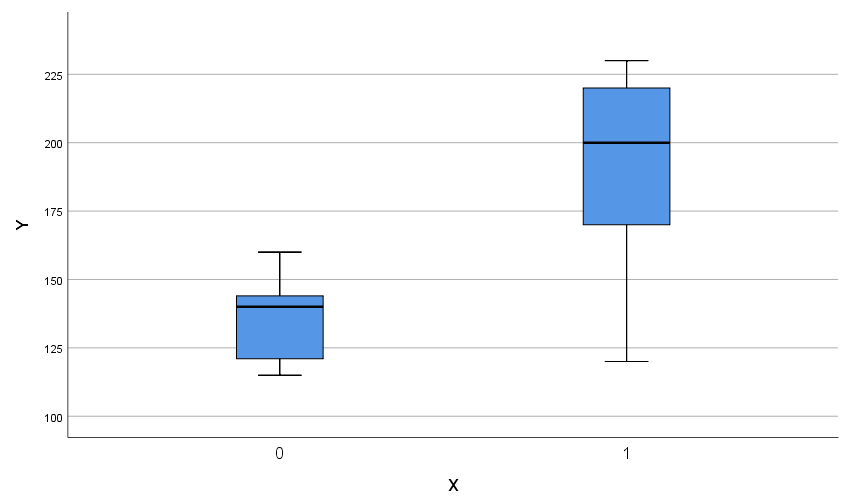
در نتیجه میتوان گفت طبق مدل، متوسط هزینههای خانوار با سرپرست زن برابر با 136.22 و با سرپرست مرد برابر با 136.22+55.22= 191.44 است. البته این میانگینها را به واسطه اجرای دستور Explore نیز میتوان بدست آورد. کافی است تنظیمات مربوطه را با توجه تصویر زیر انجام دهیم. در این پنجره کادر Dependent list مخصوص متغیر وابسته و کادر Factor list مربوط به متغیرهای مستقل است.
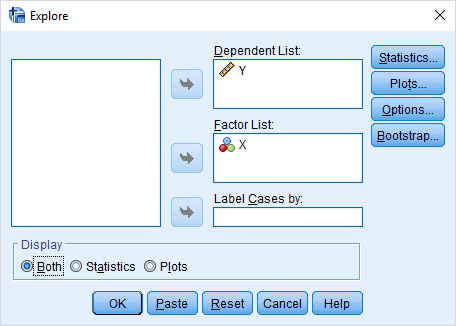
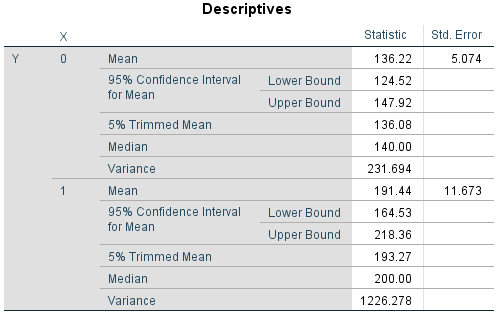
خروجی در تصویر زیر دیده میشود. آنچه که مشخص است، برابری پارامترهای مدل رگرسیونی با میانگینهای محاسبه شده توسط دستور Explore است.
نمودار «جعبهای» (Boxplot) نیز که در انتها قرار گرفته، اختلاف هزینهها در بین گروه سرپرست زن و مرد را به خوبی نشان میدهد.
با توجه به این مثال، واضح است که باید تاثیر متغیرهای طبقهای در میانگین متغیر وابسته باشد. ولی در حالتی که متغیر طبقهای بیش از دو مقدار داشته باشد، استفاده از مدل رگرسیونی به این صورت انتظار ما در تغییر میانگین را برآورده نمیکند. فرض کنید که یک متغیر مستقل (X)، مثلا میزان تحصیلات در سه طبقه داشته باشیم و ۰ به معنی میزان تحصیلات زیر دیپلم، ۱ به معنی تحصیل دانشگاهی تا کارشناسی و ۲ به معنی تحصیلات تکمیلی (کارشناسی ارشد و دکتری) باشد. حال اگر مدل رگرسیونی معمول را براساس همین مشخصات برای متغیر وابسته هزینه خانوار بسازیم، خواهیم داشت:
در این صورت اگر مقدار متغیر مستقل برابر با ۲ (تحصیلات تکمیلی) باشد، تاثیر ضریب در میانگین متغیر وابسته دو برابر بیشتر از زمانی است که متغیر مستقل برابر با ۱ (تحصیلات تا کارشناسی) باشد. همانطور که دیده میشود این رابطه همیشه برقرار نیست. ممکن است تاثیر تحصیلات تکمیلی روی هزینههای خانوار فقط کمی بیشتر از تحصیلات دانشگاهی باشد. پس بهتر است با تجزیه متغیر مستقل به چندین متغیر مستقل دو وضعیتی با مقدارهای ۰ و ۱ این نقیصه را از بین برد. متغیرهای جدید را که از تفکیک یک متغیر طبقهای با بیش از دو مقدار ایجاد میشوند، «متغیرهای مجازی» (Dummy)، «نشانگر» (Indicator) یا «طرح» (Design) مینامند.
ایجاد متغیرهای مجازی برای متغیرهای طبقهای
فرض کنید یک متغیر طبقهای با سه سطح دارید. برای مثال همان متغیر مربوط به میزان تحصیلات دانشگاهی را در نظر بگیرید.
با استفاده از دو متغیر مجازی میتوانیم طبق جدول زیر، هر سه سطح متغیر اصلی را بوسیله مقدارهای ۰ و ۱ ایجاد کنیم.
| متغیر مستقل X | متغیر مجازی | متغیر مجازی |
| 1 (تحصیل زیر دیپلم) | 0 | 0 |
| 2 (تحصیل دانشگاهی) | 1 | 0 |
| 3 (تحصیلات تکمیلی) | 0 | 1 |
به این ترتیب مدل برحسب متغیرهای مجازی به صورت زیر نوشت میشود.
برآورد پارامترهای چنین مدلی در حقیقت برآورد صحیح برای متغیر وابسته را به همراه خواهد داشت. زیرا انتظار داریم که تغییر وضعیت در متغیر مستقل از یک طبقه به طبقه دیگر در میانگین متغیر وابسته تاثیر گذار باشد، ولی شیب مدل خطی را تغییر ندهد. برای مشاهده نتیجه کافی است که به مثال زیر توجه کنید.
نکته: با توجه به تعریفی که در جدول بالا دیده میشود، مشخص است که تعداد متغیرهای مجازی همیشه یکی کمتر از سطوح مختلف متغیر طبقهای است. برای مثال اگر یک متغیر طبقهای با ۵ مقدار مختلف قرار است در مدل رگرسیون خطی به کار رود، باید با چهار متغیر مجازی با مقدارهای ۰ و ۱ به صورتی که در بالا گفته شد، جایگزین شود.
مثال ۲
براساس اطلاعات جدول زیر، میزان تحصیلات مربوط به سرپرست خانوار و هزینههای آنها مبنای ایجاد مدل رگرسیونی قرار میگیرد. متغیرهای مجازی براساس توضیحات بالا تعیین شده و در جدول اطلاعاتی گنجانده شده است.
| X | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 |
| Y | 115 | 120 | 121 | 144 | 140 | 150 | 160 | 132 | 144 |
| Z1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| Z2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| X | 3 | 3 | 3 | 3 | 3 | 2 | 2 | 2 | 1 |
| Y | 210 | 220 | 200 | 220 | 230 | 170 | 188 | 165 | 120 |
| Z1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| Z2 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
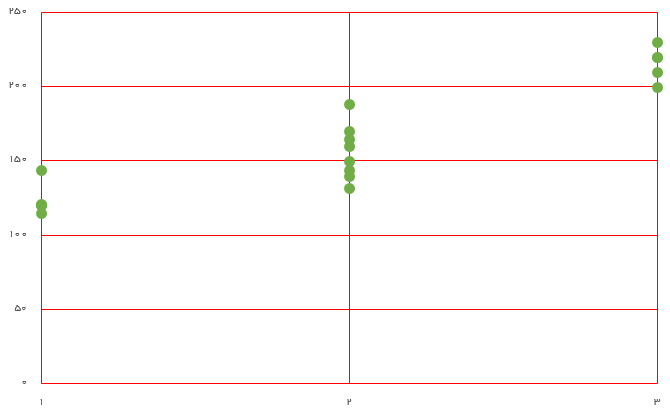
ابتدا رابطه بین دو متغیر X و Y را ترسیم میکنیم تا وجود ارتباط بینشان بررسی شود. در نمودار زیر این رابطه به خوبی قابل رویت است زیرا به سادگی میتوان دید با تغییر سطح متغیر مستقل، میزان متوسط متغیر وابسته نیز افزایش یافته است. همانطور که میدانید محور افقی مقدارهای متغیر X (تحصیلات سرپرست خانوار) و محور عمودی نیز مقدار متغیر Y (هزینه خانوار) را نشان میدهند.
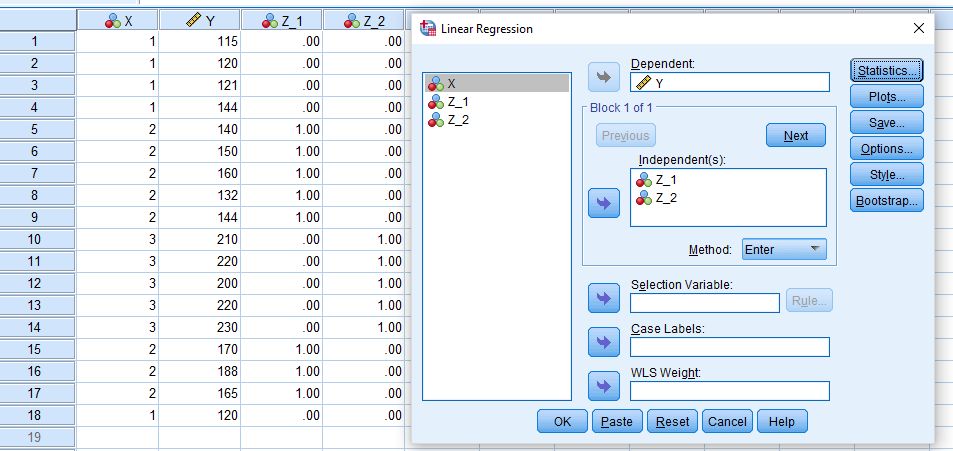
برای اجرای مدل رگرسیون با متغیرهای مستقل کمی، از نرمافزار SPSS کمک گرفته و تنظیمات مربوط به فرمان Linear را به صورت تصویر زیر در میآوریم. مشخص است که دیگر از متغیر X در مدل استفاده نمیشود و فقط متغیرهای Z1 و Z2 برای تعیین سطوح متغیر طبقهای در مدل رگرسیونی به کار رفتهاند.
با اجرای این دستور، رگرسیون خطی با استفاده از متغیرهای مجازی انجام میشود. برای دادههای مربوط به مثال ۲، خروجی به صورت زیر درخواهد آمد.
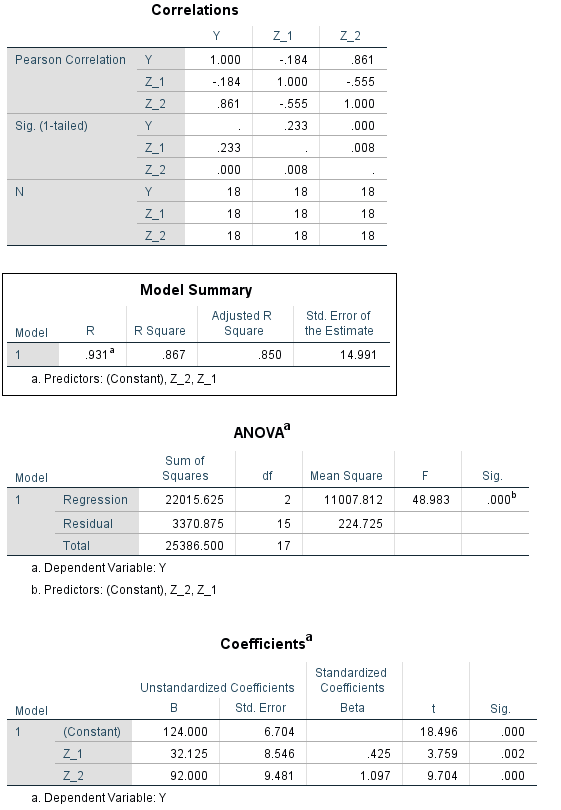
در این مدل با توجه به جدول Coefficients، پارامترهای و و بدست آمده است. همچنین مقدار Sig برای هر یک از پارامترها از احتمال خطای نوع اول که با 0.05 برابر در نظر میگیریم، کمتر است. این امر بیانگر تاثیر متغیرها روی متغیر وابسته در مدل رگرسیونی است. با توجه به ضریب همبستگی (0.867) و مربع ضریب همبستگی (0.931) که در جدول اول (Model Summary) دیده میشود، مدل بدست آمده از اعتباری خوبی هم برخوردار است.
همانطور که مشخص است، میانگین هزینه خانوار با توجه به صفر بودن هر دو متغیر مجازی (تحصیلات غیردانشگاهی) برابر با 124.00 است. اگر تحصیلات دانشگاهی باشد مقدار 32.125 به میانگین قبلی اضافه شده و برآورد هزینه خانوار را برای این گروه نشان میدهد که در اینجا برابر است با 124.00+32.125=156.125. همچنین اگر لازم است برآورد هزینه خانوار برای سرپرستهایی که مدرک تحصیلات تکمیلی دارند، محاسبه شود کافی است مقدار 92.00 به میانگین هزینه خانوار اضافه شود. در نتیجه برآورد برای این گروه برابر است با 124.00+92.00=216.00. البته این محاسبه را میتوان باز هم با دستور Explore اجرا و مشابه همین نتایج را گرفت. در تصویر زیر خروجی این دستور دیده میشود.
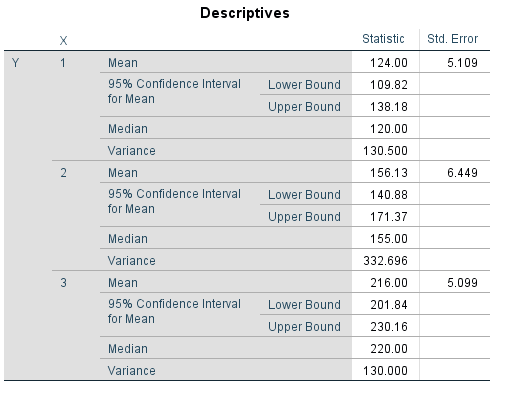
میانگین و دیگر شاخصهای توصیفی برای هر یک از گروههای تحصیلی در جدول خروجی دیده میشود.
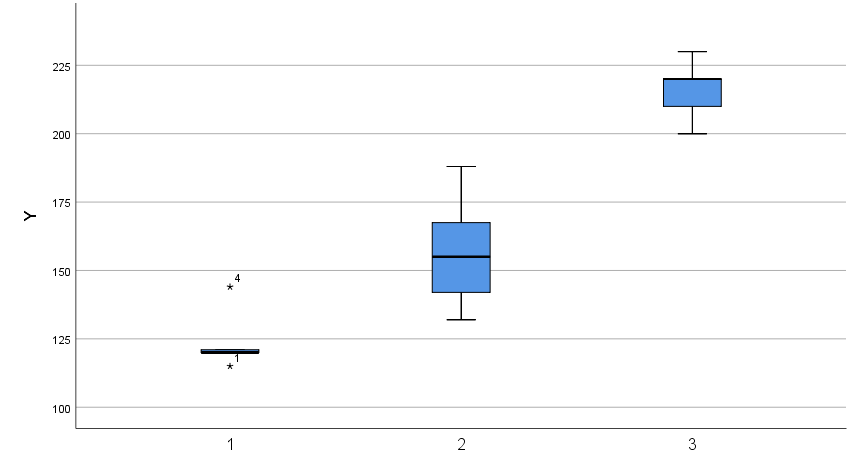
در اینجا هم نمودار جعبهای، نشانگر اختلاف بین هزینههای خانوار در سه طبقه تحصیلی مختلف است. این نتیجه نیز توسط مدل رگرسیون خطی تایید میشود.
رگرسیون چند متغیره با حضور متغیرهای مجازی و واقعی
این امکان هم وجود دارد که در رگرسیون چند متغیره، هم متغیرهای طبقهای و هم متغیرهای کمی به عنوان متغیر مستقل حضور داشته باشند. اگر متغیرهای طبقهای (مجازی) روی متغیر کمی تاثیری نداشته باشند، فقط تاثیر متغیر طبقهای در تغییر عرض از مبدا خط رگرسیون خواهد بود.
فرض کنید که دو متغیر مستقل کمی و طبقهای در مدل حضور دارند. در این حالت مدل رگرسیونی به صورت زیر در خواهد آمد:
با توجه به مقدار ۰ و ۱ برای متغیر طبقهای در حالتی که متغیر طبقهای برابر با ۱ باشد، پارامتر با مقدار ثابت جمع شده و مدل به صورت زیر در خواهد آمد:
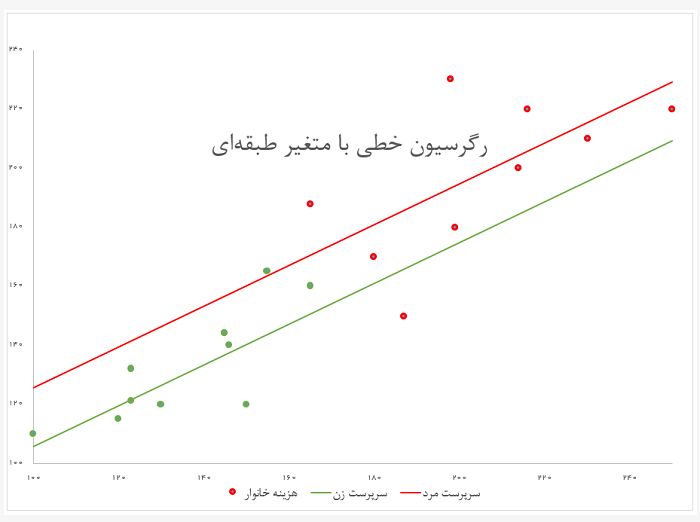
و اگر این متغیر برابر با ۰ باشد مدل تقلیل یافته و به فرم نوشته میشود. همانطور که دیده میشود، اختلاف این دو مدل فقط در عرض از مبدا است. تصویر زیر چنین حالتی را نشان میدهد . اختلافی که بین دو خط سبز و قرمز وجود دارد فقط به علت تغییر در مقدار ثابت مدل رگرسیونی است که به سبب تغییر جنسیت سرپرست خانوار ایجاد شده است. خط سبز برای نقاط سبز رنگ و خط قرمز نیز برای نقاط قرمز رنگ بهترین برازش را دارد. محور افقی در اینجا درآمد خانوار و محور عمودی نیز هزینههای خانوار را نشان میدهد. تغییر رنگ نیز به منظور نمایش جنسیت به کار رفته است.
ولی اگر متغیر طبقهای روی متغیر مستقل کمی نیز اثر داشته باشد، ممکن است هم عرض از مبدا و هم شیب خط رگرسیون تغییر کند. به این ترتیب میتوان رابطه رگرسیونی را براساس یک متغیر طبقهای (0,1) با نام و یک متغیر کمی () به عنوان متغیرهای مستقل با متغیر وابسته به صورت زیر نمایش داد:
در اینجا منظور از اثر متقابل دو متغیر مستقل روی یکدیگر است. به این ترتیب با توجه به مقدار ۰ و ۱ برای متغیر ، دو مدل به صورت زیر ساخته میشود:
به این ترتیب هم عرض از مبدا و هم شیب خط رگرسیون تغییر خواهد کرد. تصویر زیر چنین حالتی را نمایش میدهد.
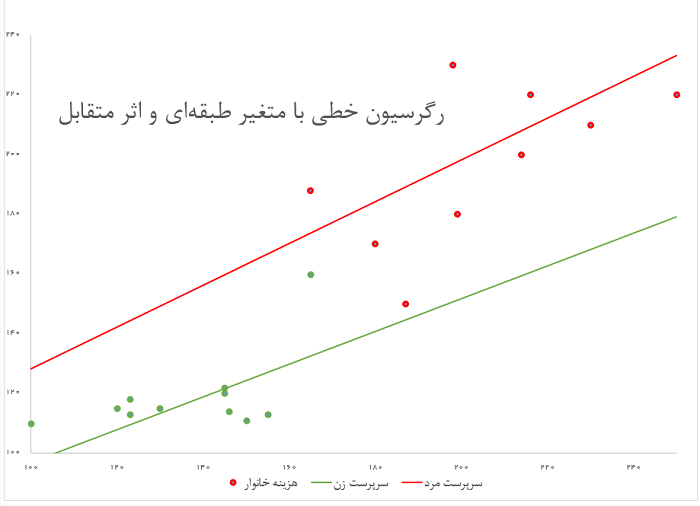
نکته: در این حالت نیز اگر متغیر طبقهای بیش از دو حالت داشته باشد، درست به مانند قبل باید آن را به چند متغیر مجازی تفکیک کرد تا نتیجه حاصل از رگرسیون خطی، معتبر باشد.
اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزش های SPSS
- مجموعه آموزش های داده کاوی یا Data Mining در متلب
- آموزش همبستگی و رگرسیون خطی در SPSS
- مهمترین الگوریتمهای یادگیری ماشین (به همراه کدهای پایتون و R) — بخش دوم: رگرسیون خطی
- آموزش یادگیری ماشین
- مجموعه آموزشهای نرمافزارهای آماری
- ضریبهای همبستگی (Correlation Coefficients) و شیوه محاسبه آنها
- مقدار احتمال (p-Value) — معیاری ساده برای انجام آزمون فرض آماری
^^













سلام وقت بخیر آیا این مطالب در باره همان رگرسیون کیفی است ؟
سلام . ممکنه درباره رگرسیون گیری از پاسخ های جمع آوری شده طبف لیکرت ای هم توضیح دهید . سپاس
سلام و درود
ضمن تشکر از متن راهنمای عالی شما
وجود تاثیر متغیر طبقهای مستقل روی متغیر مستقل کمی در مدل رگرسیون رو چطور می تونیم متوجه بشیم؟
سلام.من ورژن 23 روی ویندوز10 نصب کردم.رگرسیون خطی میگیرم ولی گراف ناقص میده. مشکل از تنظیماته یا کل نصب ایراد داره؟
سلام و تشکر از توجه شما به مطالب فرادرس
متاسفانه در نسخه ۲۳ نرم افزار SPSS رسم بعضی از نمودارها با مشکل مواجه است. یا حداقل در نسخه قفل شکسته این مشکل وجود دارد. بهتر است از نسخه های دیگر SPSS (مثلا نسخه جدید تر ۲۴) استفاده کنید.
باز هم از اینکه مشکلتان را با ما درمیان گذاشته اید متشکریم