روشهای رگرسیون در R — کاربرد در یادگیری ماشین (قسمت دوم)

در قسمت اول از روشهای رگرسیون در R با تکنیکهای رگرسیون خطی یک و چند گانه آشنا شدید. همچنین شیوه اجرای این روشهای رگرسیونی را با استفاده از کدهای R فرا گرفتید. در مباحث مربوط به این روشها در قسمت اول، فرض کردیم که متغیرهای مستقل برای مدلسازی، از نوع متغیرهای کمی هستند. شرح محاسبات و توابعی از R که مربوط به ورود متغیرهای کیفی به مدل رگرسیونی و ایجاد مدل با متغیرهای مستقل (با بیشترین تاثیر در متغیر وابسته)، از مواردی هستند که در این قسمت در مورد آنها صحبت خواهیم کرد. همچنین برای انجام محاسبات از کدهای R در محیط Rstudio استفاده و خروجیها را تحلیل خواهیم کرد.
برای آنکه با مفاهیم به کار رفته در این نوشتار آشنا باشید، پیشنهاد میشود مطلب ضریبهای همبستگی (Correlation Coefficients) و شیوه محاسبه آنها — به زبان ساده و مقدار احتمال (p-Value) — معیاری ساده برای انجام آزمون فرض آماری را مطالعه نمایید. همچنین مطالعه نوشتار بیش برازش (Overfitting)، کم برازش (Underfitting) و برازش مناسب — مفهوم و شناسایی خالی از لطف نیست.
روشهای رگرسیونی
در قسمت اول از این مبحث، پیشبینی مسافت طی شده با یک گالن سوخت را براساس متغیرهای کمی، مانند وزن خودرو، قدرت موتور و ... انجام دادیم ولی متغیرهایی مانند تعداد دنده جلو، نوع جعبه دنده و ... که متغیرهای کیفی بودند را در مدل نادیده گرفتیم. حال میخواهیم به بررسی مدل رگرسیونی با متغیرهای مستقل کمی و کیفی بپردازیم.
رگرسیون با متغیرهای کیفی
برای استفاده از متغیرهای کیفی در مدل رگرسیونی و برآورد پارامترهای مدل در R باید این متغیرها را به عنوان «عامل» (Factor) معرفی کرد. به این ترتیب هنگام انجام محاسبات این متغیرها به عنوان یک متغیر کیفی در مدل به کار میروند.
به این ترتیب تابع هنگام انجام محاسبات روی چنین متغیرهایی، آنها را تبدیل به متغیرها مجازی (Dummy Variable) کرده و عمل برآورد را انجام میدهد. اگر میخواهید از چگونگی تبدیل یک متغیر کیفی به متغیر مجازی مطلع شوید، بهتر است مطلب رگرسیون خطی با متغیرهای طبقه ای در SPSS — راهنمای گام به گام را مطالعه کنید.
برای یادآوری، جدول مربوط به اسامی متغیرها را در اینجا تکرار میکنیم. مشخص است که متغیرهای mpg, disp, hp, drat, wt و qsec همگی کمی و متغیرهای cyl, vs, am, gear و card هم کیفی هستند.
| ردیف | نام متغیر | شرح |
| ۱ | mpg | مسافت طی شده با یک گالن سوخت |
| ۲ | cyl | تعداد سیلندر (از ۴ و ۶ و ۸) |
| ۳ | disp | فضای کابین (اینچ مکعب) |
| ۴ | hp | قدرت موتور (اسب بخار) |
| ۵ | drat | نسبت اکسل عقب (چرخدندههای دیفرانسیل) |
| 6 | wt | وزن (برحسب ۱۰۰۰ پوند) |
| ۷ | qsec | زمان طی کردن یکچهارم مایل برحسب ثانیه |
| ۸ | vs | نوع موتور (0=خورجینی، ۱= خطی) |
| 9 | am | نوع گیربکس (۰= اتوماتیک و ۱= دستی) |
| ۱۰ | gear | تعداد دندههای جلو (از ۳ تا ۵) |
| 11 | carb | تعداد کاربراتور (1,2,3,6,8) |
برای تبدیل متغیرهای کیفی به عامل در مثال خودروها (mtcars) از کدهای زیر کمک میگیریم. مشخص است که تابع وظیفه این تبدیل را به عهده دارد.
1df <- mtcars %>%
2 mutate(cyl = factor(cyl),
3 vs = factor(vs),
4 am = factor(am),
5 gear = factor(gear),
6 carb = factor(carb))
7model <- mpg~disp+hp+drat+wt+cyl+vs+am+gear+carb
8summary(lm(model, df))توجه دارید که تابع مدل را برازش داده و نتایج را در متغیر model قرار داده است. با دستور خلاصهای از محاسبات صورت گرفته در خروجی ظاهر میشود که در این حالت به صورت زیر است.
1Call:
2lm(formula = model, data = df)
3
4Residuals:
5 Min 1Q Median 3Q Max
6-3.8274 -1.3781 -0.0442 0.7066 4.6051
7
8Coefficients:
9 Estimate Std. Error t value Pr(>|t|)
10(Intercept) 30.20127 11.68598 2.584 0.0200 *
11disp 0.03723 0.03077 1.210 0.2439
12hp -0.07200 0.03819 -1.885 0.0777 .
13drat 1.23511 2.41352 0.512 0.6158
14wt -4.27528 2.38914 -1.789 0.0925 .
15cyl6 -3.08642 2.75408 -1.121 0.2790
16cyl8 -1.44224 6.40763 -0.225 0.8248
17vs1 2.04951 2.77890 0.738 0.4715
18am1 0.59495 2.72917 0.218 0.8302
19gear4 1.62097 3.47874 0.466 0.6475
20gear5 2.62222 3.62889 0.723 0.4804
21carb2 -1.29955 2.11215 -0.615 0.5470
22carb3 2.94535 4.17642 0.705 0.4908
23carb4 0.37908 3.95540 0.096 0.9248
24carb6 3.94203 6.07012 0.649 0.5253
25carb8 6.83002 8.06992 0.846 0.4098
26---
27Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
28
29Residual standard error: 2.757 on 16 degrees of freedom
30Multiple R-squared: 0.892, Adjusted R-squared: 0.7907
31F-statistic: 8.807 on 15 and 16 DF, p-value: 4.281e-05همانطور که دیده میشود، متغیرهای کیفی تبدیل به متغیرهای مجازی شدهاند. برای مثال متغیر تعداد کاربراتور (carb) که مقدارهایش 1,2,3,4,6,8 است به چهار متغیر مجازی با نامهای (carb2,carb3,carb4,carb6,carb8) تبدیل شده است که مقدارهایشان ۰ یا ۱ خواهد بود. مثلاً اگر تعداد کاربراتور ۳ باشد، متغیرهای مجازی به صورت زیر مقدار دهی خواهند شد.
و در زمانی که تعداد کاربراتور برابر با ۱ باشد متغیرهای مجازی به صورت زیر خواهند بود.
به این ترتیب همه حالتهای ممکن، بوسیله مقدارهای ۰ و ۱ به کمک متغیرهای مجازی ایجاد میشوند.
نکته: همانطور که دیده میشود متغیر carb1 ایجاد نشده است. زیرا در این حالت مقدار همه متغیرهای carb2 تا carb8 برابر با صفر هستند. در نتیجه همیشه تعداد متغیرهای مجازی یکی کمتر از تعداد مقدارهایی است که متغیر کیفی خواهد داشت. از آنجایی که متغیر carb دارای شش مقدار مختلف است، پنج متغیر مجازی تولید شده است تا همه حالتهای ممکن را کدگذاری کند.
با توجه به خروجی، باز هم مانند قسمت قبل، فقط عرض از مبدا (Intercept) و قدرت موتور (hp) و وزن خودرو (wt) در مسافتی طی شده با یک گالن سوخت (mpg) موثر هستند. در نتیجه مدل به صورت زیر نوشته میشود.
البته میزان خطا برای آزمون این پارامترها در نظر گرفته شده است. در نتیجه اگر مقدار p-value که در جدول با نام دیده میشود، برای هر پارامتر کمتر از باشد در مدل نقش خواهد داشت. معمولا مقدار را سطح آزمون یا «سطح معنیداری» (Significant Level) مینامند. در قسمت پایینی جدول، راهنمای مربوط به علامتهای ***، **، *، . و ارتباط آنها با مشخص شده است. به این ترتیب اگر در انتهای سطر هر متغیری علامت *** دیده شود، فرض صفر بودن پارامتر آن متغیر در سطح معنیداری 0.001 رد میشود. همچنین اگر علامت ** در کنار سطر مربوط به متغیر در جدول دیده شود به معنی رد فرض صفر بودن آن در سطح 0.01 است. به این ترتیب علامتهای * و . به معنی سطح آزمون 0.05 و 0.1 هستند. اگر در انتهای سطر یک متغیر علامتی دیده نشود، باید آن را در مدل نادیده گرفت زیرا سطح آزمون برای رد آن برابر با ۱ است.
رگرسیون گام به گام
در این بخش، در مورد الگوریتم رگرسیون گام به گام (Stepwise Regression) بحث خواهیم کرد. هدف اصلی از این روش رگرسیونی، ساخت مدل با کمترین متغیرهای مستقل است که بیشترین تاثیر را در متغیر وابسته دارند. زمانی که تعداد متغیرهای مستقل در مدل زیاد باشد، این الگوریتم بسیار کارا بوده و بهترین مدل و پارامترها آن را برآورد میکند.
باز هم برای پیاده سازی این الگوریتم از مجموعه دادههای خودرو (mtcars) استفاده کرده و مراحل اجرا را پی میگیریم. در ابتدا بهتر است با مفهوم همبستگی بین متغیرها و «ماتریس همبستگی» (Correlation Matrix) آشنا شویم. برای مطالعه در این مورد میتوانید به مطلب ضریبهای همبستگی (Correlation Coefficients) و شیوه محاسبه آنها — به زبان ساده مراجعه کنید.
در اینجا برای نمایش میزان همبستگی متغیرها از نمودارهایی که در کتابخانه GGally وجود دارد استفاده میکنیم. این کتابخانه یک نسخه گسترش یافته از کتابخانه ggplot2 است. برای رسم نمودار همبستگی بین متغیرها از کتابخانه GGally، تابع ggscatmat را به کار میبریم. برای اطلاع از پارامترها و نحوه عملکرد این تابع میتوانید به این لینک (+) وارد شوید.
پارامترهای اصلی برای تابع ggscatmat به صورت زیر است.
1ggscatmat(df, columns = 1:ncol(df), corMethod = "pearson")
2arguments:
3-df: A matrix of continuous variables
4-columns: Pick up the columns to use in the function. By default, all columns are used
5-corMethod: Define the function to compute the correlation between variable. By default, the algorithm uses the Pearson formulaمشخص است که منظور از df منبع اطلاعاتی (DataFrame) است. همچنین پارامتر columns نیز متغیرهایی از df را تعیین میکند که باید نمودار برایشان ترسیم شود. اگر این پارامتر وارد نشود، نمودار همبستگی برای همه متغیرها ترسیم خواهد شد. همچنین پارامتر corMethod نیز شیوه محاسبه ضریب همبستگی را تعیین میکند. به طور پیشفرض شیوه محاسبه، ضریب همبستگی پیرسون است. با توجه به این توضیحات از کد زیر برای ترسیم نمودار همبستگی برای متغیرهای مربوط به منبع اطلاعاتی mtcars استفاده کردهایم. البته باز هم متغیرهای کیفی را برای محاسبات در نظر نگرفتهایم.
1library(GGally)
2df <- mtcars %>%
3 select(-c(am, vs, cyl, gear, carb))
4ggscatmat(df, columns = 1: ncol(df))به این ترتیب در قطر ماتریسی که ظاهر شده است، نمودار توزیع دادههای هر متغیر و در بالای قطر اصلی ضریب همبستگی بین متغیرها و در پایین قطر اصلی نمودار پراکندگی برای متغیرهایی که در سطر و ستون قرار گرفتهاند، ظاهر میشود.
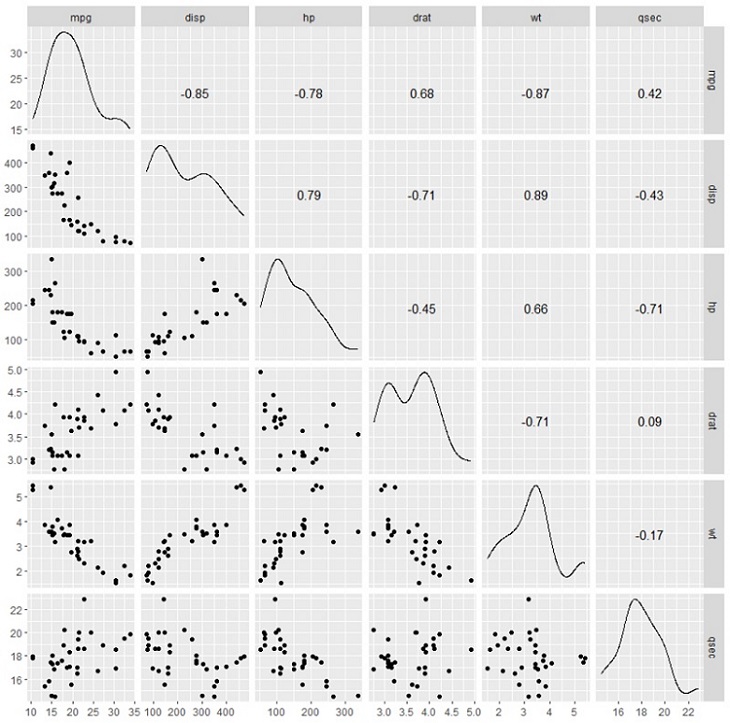
بر همین مبنا، جدول ضریب همبستگی، نمودار پراکندگی دو متغیره و همچنین نمودار توزیع دادهها برای هر متغیر در یک نمودار ظاهر شده است.
مدلها و انتخاب مدل مناسب
انتخاب متغیرهای مناسب، بخشی مهمی از برازش مدل است. رگرسیون گام به گام انتخاب متغیرهای تاثیرگذار را به طور خودکار انجام میدهد. اگر مجموعه داده شما دارای k متغیر مستقل باشد، تعداد حالاتی که میتوان مدل رگرسیونی را برازش داد برابر با است. برای مثال اگر تعداد متغیرها k=10 باشد، 1024 مدل مختلف برای برازش وجود خواهد داشت که احتیاج است همه این مدلها را ایجاد و از بین آنها بهترین مدل (برای مثال با بیشترین ) را انتخاب کنیم. به جای این کار با استفاده از رگرسیون گام به گام، بهترین مدل، بدون ایجاد همه مدلها، انتخاب و پارامترهای آن برآورد خواهد شد.
به منظور اجرای رگرسیون گام به گام از کتابخانه olsrr استفاده میکنیم. برای مقایسه مدلهای ایجاد شده از معیارهای مختلف مانند و استفاده میشود. به کمک کدهای زیر نمودار مربوط به مقایسه مقدارهای معیارهای معرفی شده ظاهر خواهد شد.
1library(olsrr)
2model <- mpg~.
3fit <- lm(model, df)
4test <- ols_step_all_possible(fit)
5View(test)
6plot(test)نکته: در اینجا مدل بوسیله .~mpg معرفی شده است به این معنی که علامت . جایگزین همه متغیرهای است که در مرحله قبل انتخاب شدهاند و باید در مدل به کار روند. در نتیجه مدل براساس متغیرهای کمی ایجاد خواهد شد.
در خروجی، ابتدا جدولی از نتایج برازش مدلهای مختلف با متغیرهای مستقل ایجاد شده و هر یک از معیارهای ارزیابی محاسبه شدهاند. در انتها با دستور نیز نمودار مربوط به نتایجی که در جدول دیده میشود ظاهر خواهد شد.

از آنجایی که ۵ متغیر مستقل در مدل معرفی شدهاند تعداد مدلهای قابل بررسی برابر است با که البته مدلی که بدون هیچ متغیر مستقلی است از مدلهای معرفی شده در جدول، کاسته شده است. در نتیجه جدول حاصل اجرای کدها دارای ۳۱ سطر است که حالتهای مختلف ترکیب متغیرهای مستقل را با یکدیگر نشان میدهد. ابتدا به بررسی جدول میپردازیم. در ستون اول (mindex) به معنی شماره مدل ثبت شده است. در ستون دوم (n) تعداد متغیرهای مورد استفاده در مدل ثبت شده است. ستونهای بعدی نیز مقدار معیارهای مختلف ارزیابی مدلها aic, sbic و ... را نشان میدهند.
نکته: ترتیب جدول براساس مقدار ستون mindex است. مدل با بهترین برازش با توجه به تعداد متغیرها (n) در شماره mindex کمتر دیده میشود. به این معنی که برای مثال حضور متغیر wt در مدلهای یک متغیره بهترین شاخص mindex را دارد در نتیجه در مقایسه با مدلهای یک متغیره از همه بهتر است. همچنین مدل با متغیرهای مستقل hp, wt بهترین مدل در بین مدلهای دو متغیره است زیرا شاخص mindex آن از بقیه مدلهای دو متغیره کمتر است.
اگر جدول را براساس معیار AIC یا (Akaike information criterion) مرتب کنیم، بهترین مدل براساس متغیرهای hp و wt ساخته خواهد شد، زیرا کم بودن AIC نشانه بهتر بودن مدل و کم بودن «بینظمی» (Entropy) در مدل است. حال به مقایسه نمودارهای ترسیم شده میپردازیم.
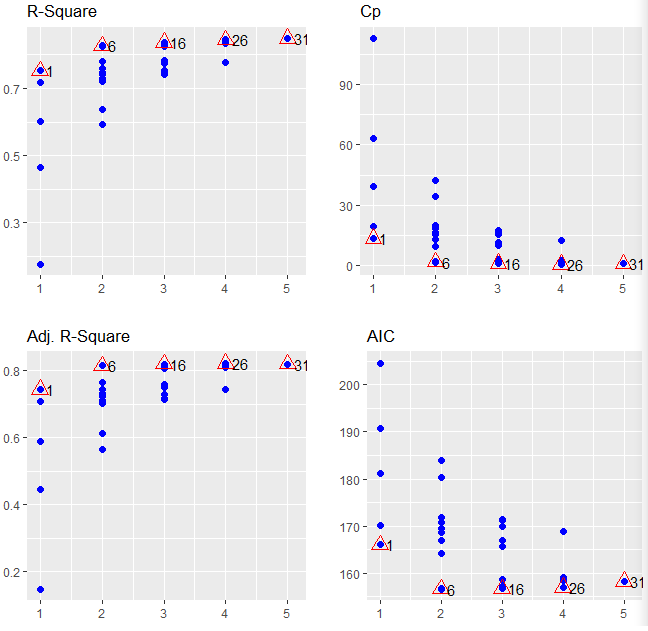
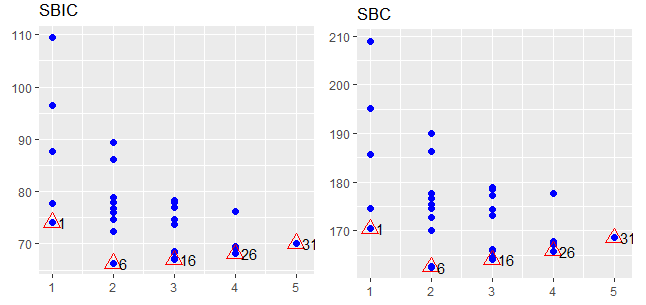
محور افقی در این نمودارها، تعداد متغیرهای مستقلی است که در مدلسازی به کار رفتهاند. از آنجایی که تعداد متغیرهای مستقل در مدلها حداکثر ۵ است، مقدارهای محور افقی از ۱ تا ۵ درجه بندی شدهاند. برای مقدار ۱ در محور افقی که نشان دهنده یک متغیر به عنوان متغیر مستقل در مدل است، تعداد مدلهای ایجاد شده برابر با ۵ است. بنابراین در هر یک از نمودارها برای مقدار ۱ در محور افقی، پنچ نقطه روی نمودار ترسیم شده است. بهترین مدل براساس هر یک از شاخصها به تفکیک تعداد متغیر، با علامت تعیین و شماره mindex نیز در کنار آن درج شده است.
براساس R-Square و Adj. R-Square، بیشترین مقدار محاسبه شده بهترین مدل را نشان میدهد ولی براساس معیارهای SBIC ,SBC و AIC کمترین مقدار بدست آمده نشانگر بهترین مدل است. خوشبختانه همه معیارها مدلهای یکسانی را به عنوان بهترین مدل معرفی کردهاند. به این ترتیب در حالت یک متغیره بهترین مدل، مدل اول با mindex=1 است. برای دو متغیره نیز بهترین مدل، شماره ۶ و برای سه متغیره شماره ۱۶، برای چهار متغیره مدل شماره ۲۶ و برای پنج متغیره مدل شماره ۳۱ است. البته در حالت ۵ متغیره همه متغیرها در مدل حضور دارند بنابراین فقط یک نقطه روی محور افقی با مقدار ۵ ظاهر شده است که مربوط به مدل ۳۱ است.
مراحل رگرسیون گام به گام
رگرسیون گام به گام یک الگوریتم تکراری است که با تکرار گامها، بهترین مدل انتخاب و پارامترهای آن برآورد میشوند. این مراحل در ادامه بررسی میشوند.
گام اول: مدل رگرسیونی، برای تک تک متغیرهای مستقل با متغیر وابسته اجرا و مقدار p-value محاسبه میشود. سپس متغیری که دارای کوچکتر از مقدار پیشفرض یا «آستانه ورود» (Entering Threshold) باشد، به مدل اضافه میشود. معمولا مقدار آستانه را 0.1 در نظر گرفته میگیرند. ولی اگر p-value یا همان هیچ متغیری کمتر از آستانه ورود نباشد، الگوریتم پایان یافته و مدل تنها با «عرض از مبدا» (Intercept) برازش میشود.
نکته: هر چند در خروجیها مقدار احتمال با عبارت نشان داده شده است ولی از جهت آنکه ذهن خواننده با عبارت p-value آشناتر است گاهی این عبارت را به کار بردهایم.
گام دوم: متغیرهای مستقل دیگر به مدل حاصل از گام اول اضافه شده و باز هم مقدار p-value محاسبه میشود. با توجه به مقدارهای محاسبه شده جدید برای p-value و آستانه ورود ممکن است متغیر جدید به مدل اضافه یا متغیرهای قبلی از مدل خارج شوند. البته برای خروج متغیر از مدل میتوان یک «آستانه خروج» (Remove Threshold) نیز در نظر گرفت که لزوما با آستانه ورود یکسان نیست. بنابراین اگر مقدار p-value متغیری که از قبل در مدل وجود داشته از آستانه خروج بیشتر باشد، از مدل خارج خواهد شد.
گام سوم: گام دوم با متغیرهای مستقل بعدی، تکرار میشود تا اینکه دیگر هیچ متغیری به مدل اضافه یا از آن حذف نشود.
در ادامه مدل رگرسیونی گام به گام را با استفاده از متغیرهای مستقل disp ,hp ,drat ,wt و qsec اجرا خواهیم کرد. ولی برای روشن شدن مراحل رگرسیون گام به گام، ابتدا فرض کنید که رگرسیون را با تک تک متغیرهای مستقل اجرا کردهایم. این کار به درک گام اول کمک میکند. مقدار p-value برای مدلهای یک متغیره در ادامه قابل مشاهده است.
1## [[1]]
2## (Intercept) disp
3## 3.576586e-21 9.380327e-10
4##
5## [[2]]
6## (Intercept) hp
7## 6.642736e-18 1.787835e-07
8##
9## [[3]]
10## (Intercept) drat
11## 0.1796390847 0.0000177624
12##
13## [[4]]
14## (Intercept) wt
15## 8.241799e-19 1.293959e-10
16##
17## [[5]
18## (Intercept) qsec
19## 0.61385436 0.01708199براساس اطلاعات مشاهده شده، مشخص است که اولین متغیر ورودی همان wt است زیرا دارای کمترین مقدار p-value است که البته از آستانه ورود نیز کمتر است. در گام دوم نیز باید یک متغیر دیگر به مدل اضافه و مقدار p-value برای ضرایب متغیرهای جدید محاسبه شود. در زیر این محاسبه صورت گرفته و قابل مشاهده است.
1## [[1]]
2## (Intercept) wt disp
3## 4.910746e-16 7.430725e-03 6.361981e-02
4##
5## [[2]]
6## (Intercept) wt hp
7## 2.565459e-20 1.119647e-06 1.451229e-03
8##
9## [[3]]
10## (Intercept) wt drat
11## 2.737824e-04 1.589075e-06 3.308544e-01
12##
13## [[4]]
14## (Intercept) wt qsec
15## 7.650466e-04 2.518948e-11 1.499883e-03در این گام نیز اضافه شدن متغیر hp که دارای کمترین مقدار p-value است بلامانع خواهد بود. مشخص است که سطر دوم شامل p-valueهای مدلی است که کمترین مقدار را دارند و البته از آستانه ورود کمتر هستند. در این هنگام اگر متغیری در مدل دارای p-value بیشتری از آستانه خروج بود، آن متغیر از مدل خارج میشود. در گام بعدی متغیرهای باقیمانده به مدل قبلی اضافه میشوند.
1## [[1]]
2## (Intercept) wt hp disp
3## 1.161936e-16 1.330991e-03 1.097103e-02 9.285070e-01
4##
5## [[2]]
6## (Intercept) wt hp drat
7## 5.133678e-05 3.642961e-04 1.178415e-03 1.987554e-01
8##
9## [[3]]
10## (Intercept) wt hp qsec
11## 2.784556e-03 3.217222e-06 2.441762e-01 2.546284e-01با توجه به اینکه هیچ یک از متغیرهای جدید قابلیت ورود به مدل را ندارند، متغیری به مدل اضافه نمیشود. از طرفی هیچ متغیری نیز قابلیت خروج از مدل را ندارد. در نتیجه مدل نهایی حاصل شده و خروجی نهایی به شکل زیر خواهد بود.
1##
2## Call:
3## lm(formula = mpg ~ wt + hp, data = df)
4##
5## Residuals:
6## Min 1Q Median 3Q Max
7## -3.941 -1.600 -0.182 1.050 5.854
8##
9## Coefficients:
10## Estimate Std. Error t value Pr(>|t|)
11## (Intercept) 37.22727 1.59879 23.285 < 2e-16 ***
12## wt -3.87783 0.63273 -6.129 1.12e-06 ***
13## hp -0.03177 0.00903 -3.519 0.00145 **
14## ---
15## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
16##
17## Residual standard error: 2.593 on 29 degrees of freedom
18## Multiple R-squared: 0.8268, Adjusted R-squared: 0.8148
19## F-statistic: 69.21 on 2 and 29 DF, p-value: 9.109e-12حال که با مراحل محاسباتی رگرسیون گام به گام آشنا شدید، انجام این محاسبات را به طور خودکار با استفاده از توابع R انجام خواهیم داد. برای اجرای الگوریتم رگرسیون گام به گام به طور خودکار در R از تابع از کتابخانه olsrr استفاده خواهیم کرد. در ادامه به بررسی پارامترهای این تابع میپردازیم. این تابع براساس p-value ورود و خروج متغیرهای مستقل در مدل را کنترل میکند.
1ols_step_both_p(fit, pent = 0.1, prem = 0.3, details = FALSE)
2arguments:
3-fit: Model to fit. Need to use `lm()`before to run `ols_stepwise()
4-pent: Threshold of the p-value used to enter a variable into the stepwise model. By default, 0.1
5-prem: Threshold of the p-value used to exclude a variable into the stepwise model. By default, 0.3
6-details: Print the details of each stepپارامتر اول یعنی fit، نتایج حاصل از رگرسیون و مدل ساخته شده توسط دستور را میپذیرد.
پارامتر دوم یا pent، مقدار p-value برای ورود متغیر (p-value enter) به مدل را تعیین میکند. در حالت پیشفرض این مقدار برابر با 0.1 در نظر گرفته شده است. به این معنی که متغیرهایی با مقدار p-value کمتر از 0.1 اجازه دارند به مدل اضافه شوند.
پارامتر سوم یا prem، مقدار p-value برای خروج متغیر (p-value remove) به مدل را مشخص میکند.
پارامتر چهارم یا details تعیین میکند که نتایج حاصل از مراحل رگرسیون گام به گام در خروجی ظاهر شود یا خیر. مقدار دهی به این پارامتر با True باعث خواهد شد که مراحل ایجاد مدل در هر گام در خروجی قابل مشاهده باشد.
حال کافی است دستور زیر را اجرا کنید. مشخص است که آستانه ورود 0.1 و آستانه خروج نیز 0.3 تعریف شده است. در اینجا متغیر fit نیز بوسیله اجرای رگرسیون روی همه متغیرها ایجاد شده است.
1ols_step_both_p(fit, pent = 0.1, prem = 0.3, details = FALSE)با اجرای دستور بالا، خروجی به همراه جزئیات و مراحل رگرسیون گام به گام ظاهر خواهد شد. در گام اول، یک متغیر وارد میشود. بدیهی است که این متغیر wt باشد. در گام دوم نیز متغیر hp وارد مدل شده و محاسبات پارامترهای مدل صورت میگیرد. از آنجایی که هیچ متغیر دیگری با مقدار p-value کمتر از آستانه ورود وجود ندارد الگوریتم پایان یافته و مدل نهایی ظاهر میشود.
1## You are selecting variables based on p value...
2## 1 variable(s) added....
3## Variable Selection Procedure
4## Dependent Variable: mpg
5##
6## Stepwise Selection: Step 1
7##
8## Variable wt Entered
9##
10## Model Summary
11## --------------------------------------------------------------
12## R 0.868 RMSE 3.046
13## R-Squared 0.753 Coef. Var 15.161
14## Adj. R-Squared 0.745 MSE 9.277
15## Pred R-Squared 0.709 MAE 2.341
16## --------------------------------------------------------------
17## RMSE: Root Mean Square Error
18## MSE: Mean Square Error
19## MAE: Mean Absolute Error
20## ANOVA
21## --------------------------------------------------------------------
22## Sum of
23## Squares DF Mean Square F Sig.
24## --------------------------------------------------------------------
25## Regression 847.725 1 847.725 91.375 0.0000
26## Residual 278.322 30 9.277
27## Total 1126.047 31
28## --------------------------------------------------------------------
29##
30## Parameter Estimates
31## ----------------------------------------------------------------------------------------
32## model Beta Std. Error Std. Beta t Sig lower upper
33## ----------------------------------------------------------------------------------------
34## (Intercept) 37.285 1.878 19.858 0.000 33.450 41.120
35## wt -5.344 0.559 -0.868 -9.559 0.000 -6.486 -4.203
36## ----------------------------------------------------------------------------------------
37## 1 variable(s) added...
38## Stepwise Selection: Step 2
39##
40## Variable hp Entered
41##
42## Model Summary
43## --------------------------------------------------------------
44## R 0.909 RMSE 2.593
45## R-Squared 0.827 Coef. Var 12.909
46## Adj. R-Squared 0.815 MSE 6.726
47## Pred R-Squared 0.781 MAE 1.901
48## --------------------------------------------------------------
49## RMSE: Root Mean Square Error
50## MSE: Mean Square Error
51## MAE: Mean Absolute Error
52## ANOVA
53## --------------------------------------------------------------------
54## Sum of
55## Squares DF Mean Square F Sig.
56## --------------------------------------------------------------------
57## Regression 930.999 2 465.500 69.211 0.0000
58## Residual 195.048 29 6.726
59## Total 1126.047 31
60## --------------------------------------------------------------------
61##
62## Parameter Estimates
63## ----------------------------------------------------------------------------------------
64## model Beta Std. Error Std. Beta t Sig lower upper
65## ----------------------------------------------------------------------------------------
66## (Intercept) 37.227 1.599 23.285 0.000 33.957 40.497
67## wt -3.878 0.633 -0.630 -6.129 0.000 -5.172 -2.584
68## hp -0.032 0.009 -0.361 -3.519 0.001 -0.050 -0.013
69## ----------------------------------------------------------------------------------------
70## No more variables to be added or removed.مدل نهایی با مقدار عرض از مبدا 37.227 و ضریب wt برابر با 3.878- و ضریب hp برابر با 0.032- مشخص شده است. در اینجا مشخص است که جدول آنالیز واریانس مطلوبیت مدل را تایید میکند زیرا مقدار sig آن (همان p-value) برابر با تقریبا صفر است.
نکته: تابع ols_step_both_p، برمبنای p-value ورود و خروج را کنترل میکند. اگر میخواهید به واسطه معیار ارزیابی مدل AIC این کار صورت گیرد، از تابع ols_step_both_aic از کتابخانه olsrr استفاده کنید.
برای خلاصهسازی مباحث گفته شده در مورد رگرسیون و توابع و رابطههای آن در R، جدول زیر میتواند موثر باشد. توجه داشته باشید که تابع هم برای متغیرهای کمی و هم برای کیفی محاسبات رگرسیون را انجام میدهد و فقط باید متغیرهای کیفی را با دستور به متغیرهای عامل تبدیل کنید.
| کتابخانه | روش رگرسیون | تابع | پارامترها | شرح |
| base | رگرسیون خطی | formula, Data | پارامترها رابطه بین متغیرها (Formula) و مجموعه داده (Data) را مشخص میکنند. | |
| base | نمایش خروجی مدل ایجاد شده | fit | خروجی مدل رگرسیونی | |
| base | نمایش ضرایب مدل رگرسیونی | $$lm()$coefficients$$ | با توجه به مدل برازش شده، ضرایب رگرسیونی را نشان میدهد. | |
| base | نمایش باقیماندهها در مدل رگرسیونی | $$lm()$residuals$$ | با توجه به مدل برازش شده، باقیماندهها را نشان میدهد. | |
| base | نمایش مقدارهای برازش شده در مدل رگرسیونی | $$lm()$fitted.values$$ | با توجه به مدل، مقدارهای برازش شده را نشان میدهد. | |
| olsrr | اجرای رگرسیون گام به گام | fit, pent = 0.1, prem = 0.3, details = FALSE | رگرسیون گام به گام برمبنای مقدار احتمال p-value را با آستانههای pent و perm اجرا میکند |
اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزش های SPSS
- مجموعه آموزشهای نرمافزارهای آماری
- مجموعه آموزش های داده کاوی یا Data Mining در متلب
- آموزش همبستگی و رگرسیون خطی در SPSS
- آموزش یادگیری ماشین
- رگرسیون خطی — مفهوم و محاسبات به زبان ساده
- رگرسیون لاسو (Lasso Regression) — به زبان ساده
- رگرسیون خطی با متغیرهای طبقه ای در SPSS — راهنمای گام به گام
- رگرسیون لجستیک (Logistic Regression) — مفاهیم، کاربردها و محاسبات در SPSS
- روشهای رگرسیون در R — کاربرد در یادگیری ماشین (قسمت اول)
^^












