ضریب همبستگی و ماتریس همبستگی در R — کاربرد در یادگیری ماشین

ارتباط بین دو متغیر کمی، از طریق محاسبه «ضریب همبستگی» (Correlation Coefficient) اندازهگیری میشود. روشهای مختلفی برای اندازهگیری ضریب همبستگی وجود دارد. در این نوشتار به بررسی دو شیوه محاسبه این ضریب با استفاده از کدهای R میپردازیم. روش اول که یک «روش پارامتری» (Parametric method) است، «ضریب همبستگی پیرسون» (Pearson Correlation Coefficient) و روش دوم نیز که روشی ناپارامتری است، «ضریب همبستگی اسپیرمن» (Spearman Correlation Coefficient) نامیده میشوند.
به منظور آگاهی بیشتر از نحوه محاسبه این دو ضریب همبستگی میتوانید مطلب ضریبهای همبستگی (Correlation Coefficients) و شیوه محاسبه آنها — به زبان ساده را مطالعه کنید. از آنجایی که محاسبه این ضرایب براساس امید ریاضی و کوواریانس صورت میگیرد، خواندن مطلب امید ریاضی (Mathematical Expectation) — مفاهیم و کاربردها نیز خالی از لطف نیست.
ضریب همبستگی و ماتریس همبستگی
منظور از همبستگی بین دو متغیر، اندازهگیری میزان پیشبینی مقدارهای یکی براساس دیگری است. به این معنی که هر چه ضریب همبستگی بیشتر باشد، امکان پیشبینی مقدار یکی از متغیرها برحسب دیگری بیشتر است.
ضریب همبستگی پیرسون و اسپیرمن بین دو مقدار ۱ و ۱- قرار دارند. به این ترتیب اگر ضریب همبستگی، مقداری نزدیک یا برابر با ۱ باشد، رابطه شدید و هم جهت بین دو متغیر وجود دارد. در این حالت میتوان گفت که جهت تغییرات هر دو متغیر شبیه یکدیگر است. به این معنی که با افزایش یکی دیگری نیز افزایش مییابد. این ارتباط براساس کاهش نیز وجود دارد، یعنی اگر یکی از متغیرها کاهش یابد، دیگری نیز کاهش خواهد یافت. در این حالت میگویند بین دو متغییر رابطه مستقیم وجود دارد. برای مثال اگر میزان درآمد افراد افزایش یابد، انتظار داریم که هزینههای زندگی نیز برایشان افزایش یابد. پس بین متغیرهای درآمد و هزینه رابطه مستقیم وجود دارد.
برعکس اگر ضریب همبستگی، مقداری نزدیک یا برابر با ۱- باشد، رابطه شدید ولی در جهت عکس بین متغیرها وجود دارد. بنابراین با افزایش یکی، دیگری کاهش خواهد یافت ولی همچنان امکان پیشبینی وجود دارد. چنین حالتی را رابطه معکوس (Inverse) مینامیم. برای مثال اگر میزان درآمد افزایش یابد، ساعات استراحت کاهش خواهد یافت زیرا برای کسب درآمد بیشتر، زمان بیشتری نیز صرف میشود، در نتیجه زمان استراحت کاهش مییابد. در ادامه برای یادآوری، مروری کوتاه بر شیوه محاسبه ضرایب همبستگی پیرسون و اسپیرمن خواهیم داشت و سپس به کدهای R برای محاسبه آنها خواهیم پرداخت.
ضریب همبستگی پیرسون
برای سنجش میزان رابطه خطی بین دو متغیر معمولا از «ضریب همبستگی خطی پیرسون» استفاده میشود که به طور خلاصه به آن ضریب همبستگی پیرسون گفته میشود. به منظور یادآوری شیوه محاسبه آن را بیان میکنیم.
اگر کوواریانس x و y را به صورت و انحراف معیار متغیر x و y را به صورت و نشان دهیم، ضریب همبستگی پیرسون با نماد یا ، به صورت زیر محاسبه میشود.
نکته: اگر ضریب همبستگی پیرسون، مقداری نزدیک صفر شود، مشخص میشود که رابطه خطی بین دو متغیر وجود ندارد. در مقابل اگر این ضریب مقداری نزدیک یا برابر با ۱ یا ۱- باشد، وجود رابطه شدید خطی بین دو متغیر تایید خواهد شد.
اگر محاسبه ضریب همبستگی براساس یک نمونه تصادفی صورت گیرد، بهتر است که برای ارزیابی نتیجه حاصل شده، از یک آزمون آماری استفاده کرد. در این حالت فرض مربوط به آزمون ضریب همبستگی پیرسون به صورت زیر نوشته میشوند.
در این حالت آماره آزمون که در ادامه بیان شده دارای توزیع t'student با n-2 درجه آزادی است. مشخص است که منظور از n نیز تعداد مشاهدات است.
ضریب همبستگی رتبهای اسپیرمن
اگر به جای استفاده از مقدارها، رتبه مقادیر برای محاسبه ضریب همبستگی به کار رود، ضریب همبستگی رتبهای اسپیرمن محاسبه شده است. بنابراین اگر «رتبه» (Rank) هر متغیر را محاسبه کرده و ضریب همبستگی پیرسون برای رتبهها را محاسبه کنیم، مقدار حاصل ر «ضریب همبستگی رتبهای اسپیرمن» مینامند که به طور خلاصه به آن ضریب همبستگی اسپیرمن گفته میشود.
بنابراین اگر بردار رتبههای متغیر را با و بردار رتبههای متغیر را با نشان دهیم، رابطه محاسباتی برای ضریب همبستگی رتبهای اسپیرمن به صورت زیر نوشته خواهد شد.
مشخص است که منظورمان کواریانس رتبههای دو متغیر یعنی و است. همچنین انحراف معیار رتبههای متغیر و همچنین نیز انحراف معیار رتبههای متغیر را نشان میدهد.
میتوان نشان داد که ضریب همبستگی رتبهای اسپیرمن نیز مانند ضریب همبستگی خطی پیرسون، مقداری بین ۱ و ۱- دارد. به این ترتیب مقدار ۱ نشان دهنده انطباق کامل بین رتبهها و مقدار ۱- نیز انطباق معکوس بین رتبهها را نشان میدهد.
نکته: از آنجایی که در محاسبه ضریب همبستگی رتبهای اسپبرمن، به جای استفاده از میانگین مقدارها، از میانگین رتبهها استفاده شده است، دادههای پرت یا دورافتاده (Outlier) در آن تاثیر کمتری نسبت به ضریب همبستگی خطی پیرسون دارند. از طرف دیگر برای انجام آزمون آماری، آماره آزمون برای ضریب همبستگی رتبهای اسپیرمن مانند آماره آزمون برای ضریب همبستگی خطی پیرسون خواهد بود.
محاسبه ضریب همبستگی پیرسون و اسپیرمن در R
به منظور محاسبه ضریب همبستگی در R از تابع استفاده میکنیم. این تابع دارای سه پارامتر است.
1cor(x, y, method)
2arguments:
3- x: First vector
4- y: Second vector
5- method: The formula used to compute the correlation. Three string values:
6 - "pearson"
7 - "kendall"
8 - "spearman"
9An optional argument can be added if the vectors contain missing value:- use = "complete.obs"پارامتر اول x است که بردار اول برای محاسبه ضریب همبستگی را نشان میدهد. همچنین پارامتر دوم یعنی y نیز بردار دوم را نشان میدهد که در محاسبه ضریب همبستگی به کار میرود. پارامتر سوم، نوع یا شیوه محاسبه ضریب همبستگی است که به صورت یک عبارت متنی، در تابع درج میشود. یکی از عبارتهای زیر میتواند مقدار این پارامتر باشد.
method = "pearson", "spearman", 'kendall"
نکته: اگر دادهها دارای مقدارهای گمشده (Missing Value) باشند، با اضافه کردن پارامتر use میتوان به کارگیری این مقدارها را در محاسبه تنظیم کرد. گزینههای مربوط به این پارامتر باید یکی از مقدارهای زیر باشد.
use = "everything", "all.obs", "complete.obs", "na.or.complete", "pairwise.complete.obs"
جدول زیر به معرفی نقش هر یک از این مقدارها در محاسبه ضریب همبستگی پرداخته است.
| مقدار پارامتر | نقش در محاسبات |
| everything | اگر یکی از مشاهدات دارای مقدار NA باشد، نتیجه محاسبات نیز NA خواهد بود. (پیشفرض) |
| all.obs | اگر یکی از مشاهدات دارای مقدار NA باشد، محاسبه با خطا مواجه خواهد شد. |
| complete.obs | اگر متغیر مربوط به یکی از مشاهدات دارای مقدار NA باشد، آن مشاهده حذف و ضریب همبستگی محاسبه میشود. اگر هیچ مشاهدهی کاملی وجود نداشته باشد، خطا ظاهر میشود. |
| na.or.complete | مانند حالت بالا ولی در صورت ناکامل بودن همه مشاهدات، به جای خطا مقدار NA را نشان میدهد. |
| pairwise.complete.obs | محاسبه ضریب همبستگی براساس مشاهداتی که برای هر دو متغیر کامل هستند. |
مثال کاربردی
در این نوشتار از مجموعه داده، هزینههای خانوار انگلستان در سالهای ۱۹۸۰ تا ۱۹۸۲ استفاده میکنیم. این بانک اطلاعاتی شامل 1519 مشاهده و 10 ویژگی یا متغیر است که در جدول زیر معرفی شدهاند.
| نام متغیر | شرح |
| wfood | سهم هزینه خوراک در سبد خانوار |
| wfuel | سهم هزینه مصرف سوخت |
| wcloth | سهم هزینه پوشاک |
| walc | سهم مصرف نوشیدنی در سبد خانوار |
| wtrans | سهم هزینه حمل و نقل |
| wother | سهم هزینههای متفرقه |
| totexp | سهم هزینههای کالا |
| income | درآمد خانوادر |
| age | سن سرپرست خانوار |
| children | دارای فرزند (۱= بدون فرزند، ۲= دارای فرزند) |
کدهای زیر به منظور بارگذاری و آمادهسازی بانک اطلاعاتی در نظر گرفته شدهاند. توجه داشته باشید که کتابخانه dplyr قبلا در R نصب شده و همچنین اتصال به اینترنت نیز برقرار باشد تا فایل اطلاعاتی قابل دریافت باشد.
1library(dplyr)
2PATH <-"https://raw.githubusercontent.com/thomaspernet/data_csv_r/master/data/british_household.csv"
3data <-read.csv(PATH) %>%
4 filter(income < 500) %>%
5 mutate(log_income = log(income),
6 log_totexp = log(totexp),
7 children_fac = factor(children, order = TRUE, labels = c("No", "Yes"))) %>%
8 select(-c(X, X.1, children, totexp, income))
9glimpse(data)در خط اول کتابخانه dplyr فراخوانی شده و سپس از طریق اینترنت فایل اطلاعاتی brithish household.csv بارگذاری شده است. این فایل در قالب متنی (CSV) بوده و فیلدها با علامت "," جدا شدهاند. بعضی از افراد در این بانک اطلاعاتی دارای درآمد بیش از ۵۰۰ هزار پوند در سال هستند. بهتر است این مشاهدات برای تحلیل کنار گذاشته شوند تا چولگی زیادی در توزیع درآمدها وجود نداشته باشد. این کار به کمک دستور (filter) که در خط چهارم نوشته شده، صورت گرفته است.
با توجه به دامنه تغییرات وسیعی که دادههای مالی و پولی دارند، بهتر است از لگاریتم (Log) آنها برای انجام محاسبات کمک گرفت. این تبدیل کمک میکند تا تاثیر ناهنجاریها و چولگی در دادهها کاهش یابد. این کار در خطوط پنجم و ششم کد ارائه شده، صورت گرفته است و لگاریتم متغیرهای income, totexp محاسبه شده و در متغیرهای log_totexp و log_income ثبت شدهاند.
همچنین به منظور تبدیل متغیر children به عامل یا فاکتور از دستور factor در خط هفتم استفاده شده است. به این ترتیب مقدار ۱ و ۲ که برای این متغیر ثبت شده بود به مقدارهای Yes و NO تغییر یافتهاند. با اجرای این کد، خروجی حاصل میشود. از آنجایی که برای نمایش دادهها از تابع استفاده شده است، متغیرهای در سطر و مقدارهایشان در ستونها دیده میشود.
1## Observations: 1,516## Variables: 10
2## $ wfood <dbl> 0.4272, 0.3739, 0.1941, 0.4438, 0.3331, 0.3752, 0...
3## $ wfuel <dbl> 0.1342, 0.1686, 0.4056, 0.1258, 0.0824, 0.0481, 0...
4## $ wcloth <dbl> 0.0000, 0.0091, 0.0012, 0.0539, 0.0399, 0.1170, 0...
5## $ walc <dbl> 0.0106, 0.0825, 0.0513, 0.0397, 0.1571, 0.0210, 0...
6## $ wtrans <dbl> 0.1458, 0.1215, 0.2063, 0.0652, 0.2403, 0.0955, 0...
7## $ wother <dbl> 0.2822, 0.2444, 0.1415, 0.2716, 0.1473, 0.3431, 0...
8## $ age <int> 25, 39, 47, 33, 31, 24, 46, 25, 30, 41, 48, 24, 2...
9## $ log_income <dbl> 4.867534, 5.010635, 5.438079, 4.605170, 4.605170,...
10## $ log_totexp <dbl> 3.912023, 4.499810, 5.192957, 4.382027, 4.499810,...
11## $ children_fac <ord> Yes, Yes, Yes, Yes, No, No, No, No, No, No, Yes, ...حال براساس این دادهها، ضریب همبستگی خطی پیرسون را برای متغیرهای «لگاریتم درآمد» (log_income) و «سهم هزینه خوراک» (wfood) را محاسبه میکنیم تا ارتباط بین آنها مشخص شود.
1cor(data$log_income, data$wfood, method = "pearson")مقدار ضریب همبستگی خطی پیرسون در این حالت برابر با 0.2466986- است که نشان دهنده ارتباط معکوس بین درآمد و هزینه خوراک است. بار دیگر از ضریب همبستگی رتبهای اسپیرمن برای اندازهگیری ارتباط بین این دو متغیر کمک میگیریم. کافی است کد را به صورت زیر اجرا کنیم.
1cor(data$log_income, data$wfood, method = "spearman")حاصل این محاسبه برابر با 0.2501252- خواهد بود که باز هم نشانگر وجود رابطه معکوس بین این دو متغیر است.
ماتریس همبستگی
برای آشنایی و درک رابطه بین دو متغیر، محاسبه ضریب «همبستگی دو متغیره» (Bivariate Correlation) میتواند مفید باشد. ولی برای نمایش همزمان رابطه بین زوجهایی از متغیرها، باید از ماتریس همبستگی (Correlation Matrix) بهره برد. عناصر این ماتریس، همبستگی بین متغیر سطرها و ستونها را نشان میدهد. البته تابع نیز ماتریس همبستگی را محاسبه میکند. کافی است که کل منبع اطلاعاتی را به عنوان پارامتر اول برای این تابع معرفی کنیم. البته توجه داشته باشید که این ماتریس، متقارن است و فقط به عناصر بالا یا پایین قطر اصلی احتیاج داریم.
برای مثال فرض کنید که میخواهیم ضریب همبستگی را برای دادههای کمی مثال قبلی اجرا کنیم. از آنجایی که متغیر children یک فاکتور یا عامل محسوب میشود، آن را در ماتریس ضریب همبستگی قرار نخواهیم داد. کد زیر، ماتریس همبستگی محاسبه کرده و نمایش میدهد.
1# the last column of data is a factor level. We don't include it in the code
2mat_1 <-as.dist(round(cor(data[,1:9]),2))
3mat_1بهتر است تابع نوشته شده را بیشتر بررسی کنیم و با پارامترهای آن آشنا شویم. در سطر دوم، با استفاده از تابع متغیرهای اول تا نهم برای محاسبه در نظر گرفته شدهاند. همچنین مقدار محاسبه شده برای ضریب همبستگی پیرسون که به صورت پیشفرض در این تابع به کار میرود، به کمک تابع تا ۲ رقم اعشار گرد شدهاند. در انتها نیز با دستور نیز خروجی تبدیل به یک ماتریس پایین مثلثی شده و در ثبت گردیده است. خروجی به صورت زیر خواهد بود.
1## wfood wfuel wcloth walc wtrans wother age log_income
2## wfuel 0.11
3## wcloth -0.33 -0.25
4## walc -0.12 -0.13 -0.09
5## wtrans -0.34 -0.16 -0.19 -0.22
6## wother -0.35 -0.14 -0.22 -0.12 -0.29
7## age 0.02 -0.05 0.04 -0.14 0.03 0.02
8## log_income -0.25 -0.12 0.10 0.04 0.06 0.13 0.23
9## log_totexp -0.50 -0.36 0.34 0.12 0.15 0.15 0.21 0.49نکته: از آنجایی که ضریب همبستگی هر متغیر با خودش برابر با ۱ است، قطر اصلی ماتریس همبستگی نمایش داده نشده است.
سطح بامعنایی (Significant Level)
برای انجام آزمون روی ضرایب همبستگی، از تابع از کتابخانه استفاده خواهیم کرد تا مقدار احتمال (p-Value) را برای هر یک از ضرایب همبستگی محاسبه کند. با استفاده از کد زیر میتوانید این کتابخانه را دریافت و بارگذاری کنیم.
1install.packages("Hmisc")
2library("Hmisc")حال به محاسبه ماتریس مقدار احتمال میپردازیم. دستور که در زیر نمایش داده شده است، این محاسبات را انجام میدهد.
1data_rcorr <-as.matrix(data[, 1: 9])
2
3mat_2 <-rcorr(data_rcorr)
4# mat_2 <-rcorr(as.matrix(data)) returns the same output
5mat_2
6p_value <-round(mat_2[["P"]], 3)
7p_valueبا اجرای این کد، ابتدا ماتریس ضریب همبستگی مشابه حالت قبل محاسبه میشود و در انتها نیز ماتریس مقدار احتمال ظاهر خواهد شد.
نکته: دستور هر دو ماتریس ضرایب و مقدار احتمال را محاسبه میکند و آن را در یک «لیست» (List) قرار میدهد. عناصر این لیست به ترتیب، r یا ماتریس همبستگی، n تعداد مشاهدات و P یا ماتریس مقدار احتمال است. برای دسترسی به قسمت p-value در این لیست از دستور استفاده کردهایم.
به این ترتیب خروجی به صورت زیر ظاهر خواهد شد.
1 wfood wfuel wcloth walc wtrans wother age log_income log_totexp
2wfood NA 0.000 0.000 0.000 0.000 0.000 0.365 0.000 0
3wfuel 0.000 NA 0.000 0.000 0.000 0.000 0.076 0.000 0
4wcloth 0.000 0.000 NA 0.001 0.000 0.000 0.160 0.000 0
5walc 0.000 0.000 0.001 NA 0.000 0.000 0.000 0.105 0
6wtrans 0.000 0.000 0.000 0.000 NA 0.000 0.259 0.020 0
7wother 0.000 0.000 0.000 0.000 0.000 NA 0.355 0.000 0
8age 0.365 0.076 0.160 0.000 0.259 0.355 NA 0.000 0
9log_income 0.000 0.000 0.000 0.105 0.020 0.000 0.000 NA 0
10log_totexp 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 NAنمایش ماتریس همبستگی
معمولا برای نمایش تصویری ضرایب همبستگی از «نقشه گرمایی» (Heat Map) استفاده میشود. برای ترسیم چنین نموداری از کتابخانه کمک میگیریم که به کمک دستورات زیر میتوانید آن را بارگذاری و نصب کنید.
1install.packages("GGally")
2library(GGally)این کتابخانه دارای توابع مختلفی در زمینه رسم نمودارهای مختلف آماری است که برای نمایش ضریب همبستگی و توزیع به کار میرود. در اینجا از تابع بهره میبریم.
1ggcorr(df, method = c("pairwise", "pearson"),
2 nbreaks = NULL, digits = 2, low = "#3B9AB2",
3 mid = "#EEEEEE", high = "#F21A00",
4 geom = "tile", label = FALSE,
5 label_alpha = FALSE)
6arguments:
7- df: Dataset used
8- method: Formula to compute the correlation. By default, pairwise and Pearson are computed
9- nbreaks: Return a categorical range for the coloration of the coefficients. By default, no break and the color gradient is continuous
10- digits: Round the correlation coefficient. By default, set to 2
11- low: Control the lower level of the coloration
12- mid: Control the middle level of the coloration
13- high: Control the high level of the coloration
14- geom: Control the shape of the geometric argument. By default, "tile"
15- label: Boolean value. Display or not the label. By default, set to `FALSE`پارامترهای این تابع در جدول زیر معرفی شدهاند.
| پارامتر | عملکرد |
| df | معرفی منبع اطلاعاتی |
| method | روش محاسبه ضریب همبستگی (پیشفرض ضریب همبستگی پیرسون بین زوجها) |
| nbreak | تعداد شکست و طبقهبندی ضرایب همبستگی (پیشفرض بدون شکست و رنگها پیوسته) |
| digits | تعداد ارقام برای گردن کردن ضریب همبستگی |
| low | کد رنگ برای کمترین مقدار ضریب همبستگی |
| mid | کد رنگ برای میانگین مقدار ضریب همبستگی |
| high | کد رنگ برای حداکثر مقدار ضریب همبستگی |
| geom | کنترل نحوه قرارگیری عناصر تصویری روی نمودار در حالت پیشفرض به صورت کاشی |
| label | مقدار منقطی به منظور نمایش مقدار ضریب همبستگی روی نقشه گرمایی (پیشفرض FALSE- بدون نمایش) |
حال دستور مربوط به نمایش نقشه گرمایی را برای منبع اطلاعاتی data اجرا میکنیم. کافی است که دستور زیر را در R اجرا کنید.
1ggcorr(data)همانطور که دیده میشود، این تابع احتیاج به فقط یک پارامتر دارد که همان منبع اطلاعاتی (df) است. در این حالت خروجی به صورت زیر نمایش داده خواهد شد. (رنگها به صورت پیشفرض از آبی کم رنگ تا قرمز در نظر گرفته شدهاند.)
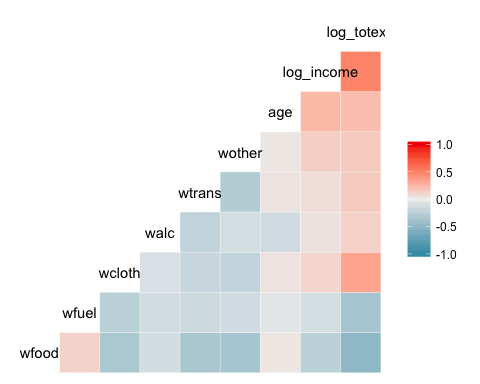
به منظور کنترل بیشتر روی نقشه گرمایی، پارامترها را تغییر میدهیم و دستور را به صورت زیر مینویسم.
1ggcorr(data,
2 nbreaks = 6,
3 low = "steelblue",
4 mid = "white",
5 high = "darkred",
6 geom = "circle")با این کار سطوح مربوط به رنگ ها با پارامتر breaks به ۶ قسمت تفکیک شده است. همچنین سه سطح رنگ نیز به صورت آبی تا قرمز تیره تنظیم شده است. نحوه نمایش نقشه گرمایی هم براساس دایرهها توسط پارامتر "geom="circle تعیین شده است.
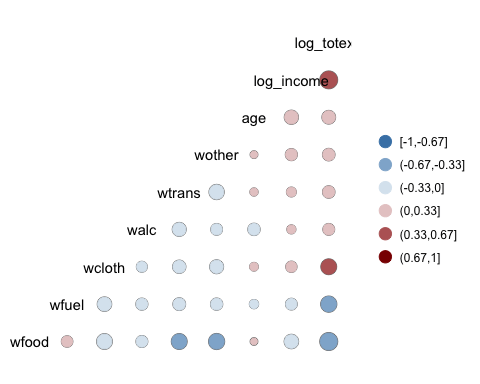
اگر بخواهید مقدار ضرایب همبستگی را روی نمودار نمایش دهید باید پارامتر label را مقدار دهی کنید. به این منظور کد زیر را اجرا کنید تا نمایش نقشه گرمایی، زیباتر شود.
1ggcorr(data,
2 nbreaks = 6,
3 label = TRUE,
4 label_size = 3,
5 color = "grey50")نکته: پارامتر lable=TRUE باعث نمایش ضرایب همبستگی روی نقشه شده است. همچنین اندازه برچسبها (label_size) و رنگ آنها (color) نیز قابل تعیین است.
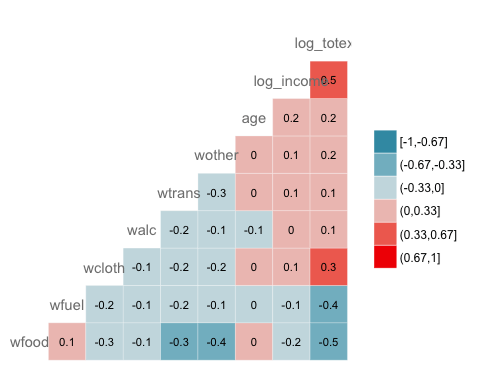
شیوه دیگر برای محاسبه و نمایش ضرایب همبستگی با استفاده از تابع از کتابخانه است. در این تابع، نمودار توزیع حاشیهای (برای هر متغیر)، ضریب همبستگی و ... قابل نمایش است. شکل این تابع در زیر نشان داده شده است.
1ggpair(df, columns = 1: ncol(df), title = NULL,
2 upper = list(continuous = "cor"),
3 lower = list(continuous = "smooth"),
4 mapping = NULL)
5arguments:
6- df: Dataset used
7- columns: Select the columns to draw the plot
8- title: Include a title
9- upper: Control the boxes above the diagonal of the plot. Need to supply the type of computations or graph to return. If continuous = "cor", we ask R to compute the correlation. Note that, the argument needs to be a list. Other arguments can be used, see the [vignette]("http://ggobi.github.io/ggally/#custom_functions") for more information.
10- Lower: Control the boxes below the diagonal.
11- mapping: Indicates the aesthetic of the graph. For instance, we can compute the graph for different groups.همانطور که مشخص است شش پارامتر برای این تابع وجود دارد. جدول زیر به معرفی این پارامترها پرداخته است.
| پارامتر | عملکرد |
| df | معرفی منبع اطلاعاتی |
| column | انتخاب ستونهایی از df که در محاسبات به کار میروند. |
| title | عنوان نمودار |
| upper | تعیین عناصری که در بالای قطر اصلی نمایش داده میشوند |
| lower | تعیین عناصری که در پایین قطر اصلی نمایش داده میشوند |
| mapping | تفکیک نقشه گرمایی برحسب متغیر عامل یا فاکتور |
به این ترتیب در ادامه با استفاده از تابع یک نقشه گرمایی با عناصر مختلف ایجاد میکنیم. کد مربوطه با R در زیر دیده میشود.
1ggpairs(data, columns = c("log_totexp", "log_income", "age", "wtrans"),
2 title = "Bivariate analysis of revenue expenditure by the British household",
3 upper = list(continuous = wrap("cor",
4 size = 3)),
5 lower = list(
6 continuous = wrap("smooth",
7 alpha = 0.3,
8 size = 0.1))
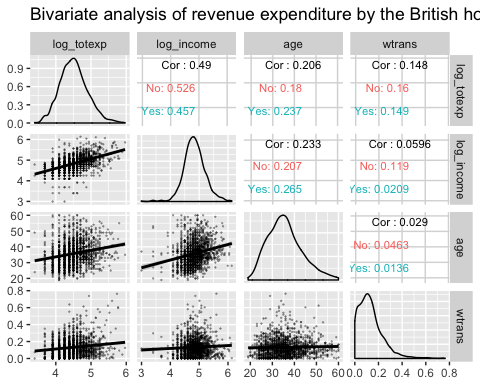
9)با اجرای این کد، نقشه گرمایی برای چهار متغیر و ضرایب همبستگی آنها ترسیم شده است.
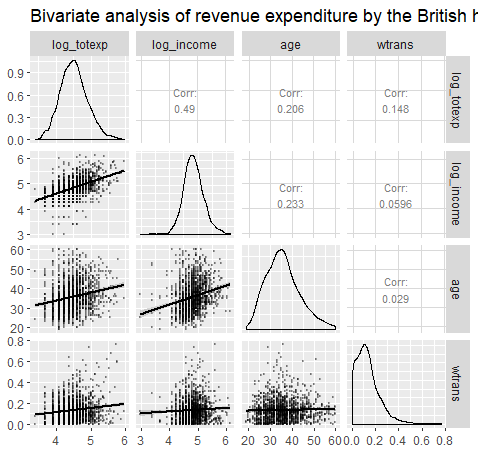
پارامترهای این دستور در ادامه بیشتر توضیح داده خواهند شد.
Column: متغیرهایی که در محاسبه ضریب همبستگی و ترسیم نمودار نقش دارند در پارامتر Column معرفی شدهاند. اسامی این متغیرها را در زیر میبینید.
"log_totexp", "log_income", "age", "wtrans".
Title: برای نمایش یک عنوان بر روی نمودار از پارامتر title استفاده میشود.
upper: این پارامتر یک لیست است که اجزای نمایش داده شده در بالای قطر اصلی را تعیین میکند. همانطور که در نقشه گرمایی پایین میبینید مقدار ضریب همبستگی یا corr باید نمایش داده شود. در قسمت size نیز اندازه برای نمایش این مقدارها تعیین شده است. در اینجا تابع wrap باعث میشود عناصر معرفی شده در لیست هر یک در خطوط مجزا ظاهر شوند.
mapping: این پارامتر نیز باعث میشود در هر قسمت از نقشه گرمایی، اجزای قابل نمایش که در بخش upper و lower تعیین شدهاند برحسب یک متغیر عامل تفکیک شوند. بر این اساس اطلاعاتی که باید نمایش داده شود برای خانوارهایی که بدون فرزند هستند از رنگ قرمز و برای نمایش اطلاعاتی خانوارهایی که دارای فرزند هستند از رنگ آبی استفاده شده است.
lower: این پارامتر نیز به مانند upper یک لیست است که در این حالت نمودار رابطه خطی (smooth) بین زوج متغیرها را ترسیم کرده است. مقدار alpha نیز میزان شفافیت نقاطی را تعیین میکند که روی نمودار ظاهر شدهاند.
به این ترتیب، به منظور تفکیک خروجی براساس وضعیت فرزندان در خانوار کافی است که کدها را به صورت زیر تغییر دهید.
1library(ggplot2)
2ggpairs(data, columns = c("log_totexp", "log_income", "age", "wtrans"), title = "Bivariate analysis of revenue expenditure by the British household",
3 upper = list(continuous = wrap("cor",
4 size = 3)),
5 lower = list(continuous = wrap("smooth",
6 alpha = 0.3,
7 size = 0.1)),
8 mapping = aes(color = children_fac))با این کار در قسمت بالای قطر اصلی نقشه گرمایی، خروجیها به تفکیک وضعیت فرزندان خانوارها مشخص شده است.
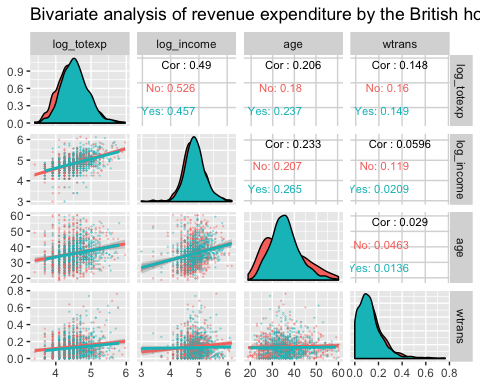
همچنین اگر میخواهید که نقشه گرمایی در قسمت نمودارها نیز برای گروه خانوارهای دارای فرزند و یا بدون فرزند ترسیم شود از کدهای زیر استفاده کنید.
1library(ggplot2)
2ggpairs(data, columns = c("log_totexp", "log_income", "age", "wtrans"), title = "Bivariate analysis of revenue expenditure by the British household",
3 upper = list(continuous = wrap("cor",
4 size = 3)),
5 lower = list(continuous = wrap("smooth",
6 alpha = 0.3,
7 size = 0.1)),
8 mapping = aes(color = children_fac))همانطور که مشاهده میکنید، در این نمودار، از کتابخانه و تابع برای رسم نمودار استفاده شده است. به این ترتیب خروجی به صورت زیر در خواهد آمد.
خلاصه توابع
در جدول زیر خلاصهای از توابع به کار رفته در این مطلب یادآوری شدهاند.
| کتابخانه | عملکرد | روش | کد |
| Base | ضریب همبستگی دو متغیر | پیرسون | cor(x1,x2, method = "pearson") |
| Base | ضریب همبستگی دو متغیر | اسپیرمن | cor(x1,x2, method = "spearman") |
| Base | ضریب همبستگی چند متغیره | پیرسون | cor(df, method = "pearson") |
| Base | ضریب همبستگی چند متغیره | اسپیرمن | cor(df, method = "spearman") |
| hmisc | مقدار احتمال (p Value) | rcorr(as.matrix(df[))[["P"]] | |
| GGally | نقشه گرمایی | ggcorr(df) |
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزش های SPSS
- مجموعه آموزشهای نرمافزارهای آماری
- مجموعه آموزش های داده کاوی یا Data Mining در متلب
- آموزش یادگیری ماشین
- رگرسیون خطی — مفهوم و محاسبات به زبان ساده
- ضریبهای همبستگی (Correlation Coefficients) و شیوه محاسبه آنها — به زبان ساده
- ضریب همبستگی جزئی (Partial Correlation) — به زبان ساده
- روشهای رگرسیون در R — کاربرد در یادگیری ماشین (قسمت اول)
- روشهای رگرسیون در R — کاربرد در یادگیری ماشین (قسمت دوم)
^^













با سلام.
توی قسمت کد نویسی محاسبه ضریب همبستگی Spearman، به جای cor، به اشتباه or نوشته شده.
با سلام و احترام؛
سپاس از دقت نظر شما. این مورد اصلاح شد.
با تشکر از همراهی شما با مجله فرادرس
با سلام
اولا ممنون بخاطر زحمتي كه در ترجمه كشيده بوديد و اينكه در معرفي نرم افزار R نقشي ايفا كرديد قابل ستايش است ولي اي كاش حداقل اولين اصل در كار علمي يعني رفرنس دهي را رعايت ميكرديد و اشاره اي به اصل مقاله كه از آن “ترجمه” صورت گرفته را عنوان ميكرديد.
با تشكر.
سلام، وقت شما بخیر؛
منبع تمامی مطالب مجله فرادرس در صورتیکه اقتباس یا ترجمه از سایت یا مرجع دیگری صورت گرفته باشد در انتهای آنها ذکر شده است.
از اینکه با مجله فرادرس همراه هستید و با نظرات خود به ما در بهبود آن یاری میرسانید از شما سپاسگزاریم.