میانه مثلث چیست؟ + تعریف، فرمول محاسبه، قوانین و خواص

میانه مثلث، پاره‌خطی است که راس یک چندضلعی را به مرکز ضلع نظیر راس (ضلع مقابل) وصل می‌کند. برای آشنایی با این مفهوم، ابتدا باید با تعاریف مرتبط با مثلث و اجزای مختلف آن نظیر راس و ضلع آشنا باشید. مثلث، یک شکل بسته است. این شکل، از اتصال سه خط شکسته تشکیل می‌شود. به خط‌های تشکیل‌دهنده مثلث، ضلع و به محل اتصال ضلع‌ها، راس می‌گویند. در مثلث، اندازه‌های دیگری نظیر زاویه، ارتفاع، میانه و غیره نیز تعریف می‌شود. در این مقاله، به معرفی میانه در انواع مثلث (نظیر مثلث قائم‌الزاویه، متساوی‌الاضلاع و غیره)، قوانین و فرمول‌های محاسبه آن به همراه حل چند مثال مرتبط می‌پردازیم.

میانه در مثلث چیست؟

«میانه» (Median)، پاره‌خط اتصال‌دهنده راس‌های مثلث به وسط ضلع مقابل آن‌ها است. میانه‌های مثلث، ضلع‌های آن را به دو قسمت مساوی تقسیم می‌کنند.

فیلم آموزش ریاضی پایه هفتم – جامع و با نکات مهم در فرادرس

کلیک کنید

مثلث زیر را در نظر بگیرید. این مثلث، از سه راس «الف»، «ب» و «ج» و سه ضلع «الف-ب»، «ب-ج» و «ج-الف» تشکیل می‌شود.

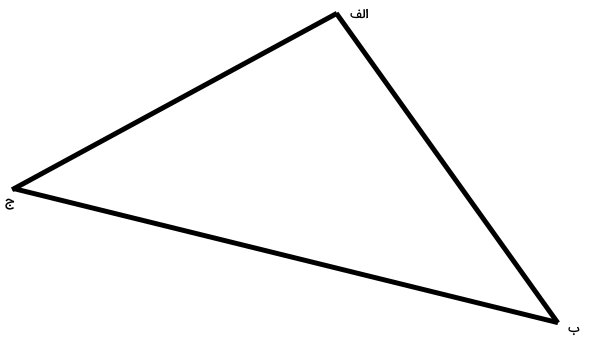
یکی از ضلع‌های مثلث بالا (در اینجا ضلع الف-ب) را به دو قسمت مساوی تقسیم کرده و مرکز ضلع را با حرف «د» مشخص می‌کنیم.

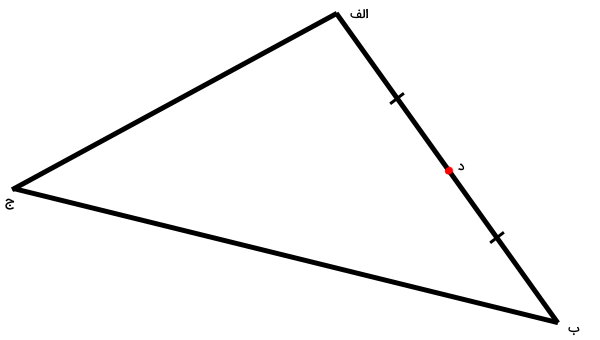
نقطه د، وسط ضلع الف-ب است. اکنون، یک پاره‌خط از راس مقابل ضلع الف-ب (راس ج) تا نقطه د رسم می‌کنیم.

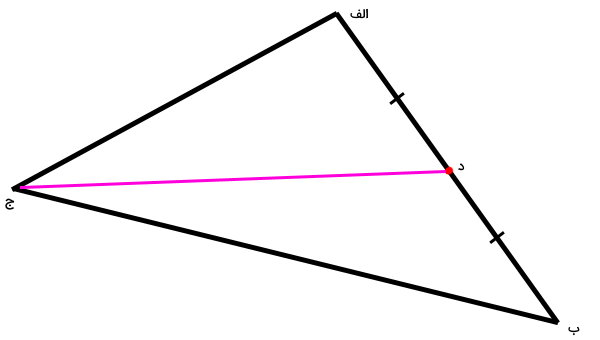
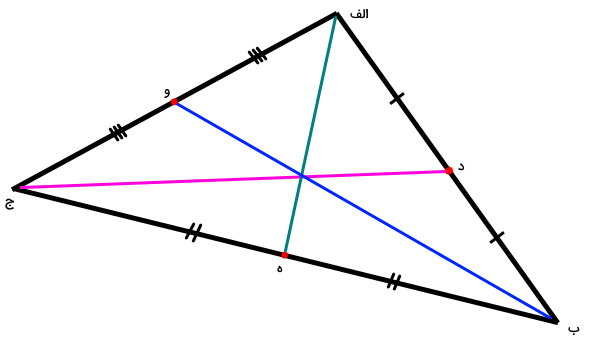
پاره‌خط «ج-د»، راس ج را به مرکز ضلع الف-ب وصل می‌کند. این پاره‌خط، یکی از میانه‌های مثلث «الف-ب-ج» است. با تکرار این کار برای ضلع‌های ب-ج و ج-الف، دو میانه دیگر مثلث رسم می‌شوند. بنابراین، هر مثلث، سه میانه دارد.

میانه در آمار

مفهوم میانه، در آمار توصیفی نیز مورد استفاده قرار می‌گیرد. مجموعه‌ای از داده‌های عددی را در نظر بگیرید که از بزرگ به کوچک یا از کوچک به بزرگ مرتب شده‌اند. به عددی که نصف داده‌ها از آن بزرگ‌تر و نصف داده‌ها از آن کوچک‌تر باشند، به عنوان میانه در نظر گرفته می‌شود. در واقع، مانند مفهوم میانه در مثلث، میانه در آمار نیز به نصف یا وسط چیزی اشاره می‌کند.

فیلم آموزش آمار و احتمال – پایه یازدهم در فرادرس

کلیک کنید

خواص میانه مثلث چه هستند ؟

میانه، یکی از اندازه‌های مهم در هر مثلث است. خواص میانه و قوانین مربوط به آن، کاربردهای گسترده‌ای در محاسبه دیگر اندازه‌های مثلث دارند. از مهم‌ترین قوانین میانه در مثلث می‌توان به موارد زیر اشاره کرد:

• هر مثلث، سه میانه دارد.
• میانه هر ضلع، آن ضلع را به دو پاره‌خط با طول‌های مساوی تقسیم می‌کند.
• فارغ از شکل مثلث، هر سه میانه آن، همدیگر را در یک نقطه مشترک قطع می‌کنند.
• محل تقاطع سه میانه در مثلث، بر روی مرکز ثقل و مرکز هندسی مثلث قرار دارد.
• هر میانه، مثلث را به دو مثلث کوچک‌تر با مساحت‌های برابر تقسیم می‌کند. در مجموع، با رسم سه میانه مثلث، شش مثلث کوچک‌تر با مساحت‌های مساوی به وجود می‌آید.

قوانین مرتبط با میانه‌های مثلث به موارد بالا ختم نمی‌شود. برخی دیگر از خواص میانه عبارت هستند از:

• اندازه هر میانه مثلث، از مجموع دو میانه دیگر کوچک‌تر است.
• اندازه هر میانه مثلث، از نصف مجموع دو ضلع دیگر کوچک‌تر بوده و از نصف تفاضل آن دو ضلع بزرگ‌تر است.
• محل تقاطع میانه‌های مثلث، آن‌ها را به دو قسمت با نسبت ۱ به ۲ تقسیم می‌کند. فاصله این محل بر روی یک میانه تا راس نظیر آن، به اندازه یک‌سوم طول میانه و تا ضلع نظیر، به اندازه دو سوم طول میانه است.
• بزرگ‌ترین میانه مثلث، به کوچک‌ترین ضلع آن وارد می‌شود و کوچک‌ترین میانه مثلث، به بزرگ‌ترین ضلع آن وارد می‌شود.
• مجموع مربعات میانه‌های مثلث، برابر با سه‌چهارم مجموع مربعات ضلع‌های آن است.

به راسی که میانه از آن رسم می‌شود، راس نظیر میانه می‌گویند. به ضلعی که میانه بر آن وارد می‌شود نیز ضلع نظیر میانه می‌گویند.

اندازه میانه مثلث چگونه بدست می آید ؟

اندازه میانه، به اندازه ضلع‌های مثلث بستگی دارد. از این‌رو، فرمول میانه مثلث، با توجه به اندازه ضلع‌ها نوشته می‌شود.

فیلم آموزش هندسه پایه دهم – هندسه 1 در فرادرس

کلیک کنید

برای آشنایی با فرمول میانه، مثلث زیر را در نظر بگیرید.

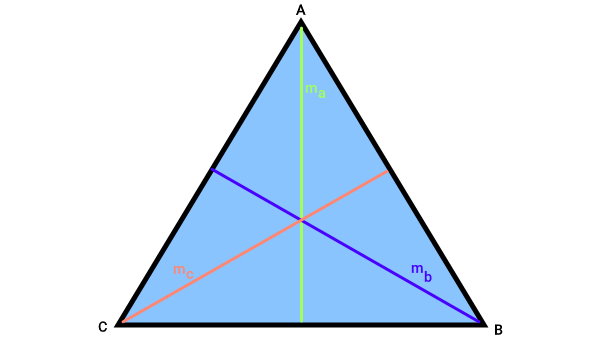
میانه معمولا با حرف انگلیسی m نمایش داده می‌شود. حرف m، ابتدای عبارت «Median» به معنای «میانه» است. به منظور مشخص کردن میانه نظیر هر راس، حرف کوچک آن به عنوان اندیس در کنار حرف m آورده می‌شود. به عنوان مثال، منظور m_a، میانه نظیر راس A است. اگر بخواهیم طول میانه وارد بر ضلع BC را به دست بیاوریم، از فرمول زیر استفاده می‌کنیم:

$$m _ a = \sqrt { \frac { ۲ b ^ ۲ + ۲ c ^ ۲ - a ^ ۲ }{ ۴ } }$$

• m_a: میانه ضلع BC
• a: طول ضلع BC
• b: طول ضلع AC
• c: طول ضلع AB

فرمول محاسبه طول میانه وارد بر ضلع‌های AC و AB‌ نیز به همین صورت نوشته می‌شود:

$$m _ b = \sqrt { \frac { ۲ a ^ ۲ + ۲ c ^ ۲ - b ^ ۲ }{ ۴ } }$$

$$m _ c = \sqrt { \frac { ۲ a ^ ۲ + ۲ b ^ ۲ - c ^ ۲ }{ ۴ } }$$

• m_b: میانه ضلع AC
• m_c: میانه ضلع AB

مثال ۱: محاسبه اندازه میانه مثلث

اندازه میانه‌های مثلث زیر را به دست بیاورید.

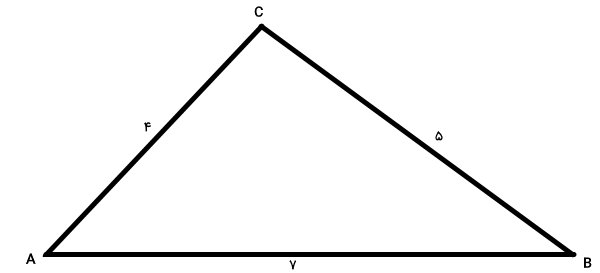
مثلث بالا، دارای سه ضلع به اندازه‌های ۴، ۵ و ۷ است. برای درک بهتر مسئله، میانه‌های وارد بر هر ضلع را رسم می‌کنیم.

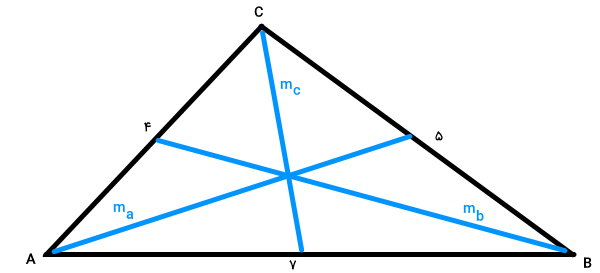
با توجه به میانه‌های رسم شده داریم:

• m_a: میانه ضلع BC
• m_b: میانه ضلع AC
• m_c: میانه ضلع AB

اندازه هر یک از این میانه‌ها با استفاده از فرمول‌های زیر به دست می‌آید:

$$m _ a = \sqrt { \frac { ۲ b ^ ۲ + ۲ c ^ ۲ - a ^ ۲ }{ ۴ } }$$

$$m _ b = \sqrt { \frac { ۲ a ^ ۲ + ۲ c ^ ۲ - b ^ ۲ }{ ۴ } }$$

$$m _ c = \sqrt { \frac { ۲ a ^ ۲ + ۲ b ^ ۲ - c ^ ۲ }{ ۴ } }$$

• a: طول ضلع BC
• b: طول ضلع AC
• c: طول ضلع AB

فرمول‌های بالا را به صورت زیر بازنویسی می‌کنیم:

$$m _ a = \sqrt { \frac { ۲ AC ^ ۲ + ۲ AB ^ ۲ - BC ^ ۲ }{ ۴ } }$$

$$m _ b = \sqrt { \frac { ۲ BC ^ ۲ + ۲ AB ^ ۲ - AC ^ ۲ }{ ۴ } }$$

$$m _ c = \sqrt { \frac { ۲ BC ^ ۲ + ۲ AC ^ ۲ - AB ^ ۲ }{ ۴ } }$$

• طول ضلع BC برابر با ۵ است.
• طول ضلع AC برابر با ۴ است.
• طول ضلع AB برابر با ۷ است.

مقادیر معلوم را درون هر یک از فرمول‌‌‌ها قرار می‌دهیم. این کار را با میانه وارد بر ضلع BC‌ شروع می‌کنیم:

$$m _ a = \sqrt { \frac { ( ۲ \times ۴ ^ ۲ ) + ( ۲ \times ۷ ^ ۲ ) - ۵ ^ ۲ }{ ۴ } }$$

$$m _ a = \sqrt { \frac { ( ۲ \times ۱۶ ) + ( ۲ \times ۴۹ ) - ۲۵ }{ ۴ } }$$

$$m _ a = \sqrt { \frac { ۳۲ + ۹۸ - ۲۵ }{ ۴ } }$$

$$m _ a = \sqrt { \frac { ۱۰۵ }{ ۴ } }$$

$$m _ a = \sqrt { ۲۶/۲۵ }$$

$$m _ a = ۵/۱۲$$

اندازه میانه نظیر راس A برابر با ۵/۱۲ است. به همین ترتیب، محاسبه اندازه دو میانه بعدی مثلث را انجام می‌دهیم:

$$m _ b = \sqrt { \frac { ( ۲ \times ۵ ^ ۲ ) + ( ۲ \times ۷ ^ ۲ ) - ۴ ^ ۲ }{ ۴ } }$$

$$m _ b = \sqrt { \frac { ( ۲ \times ۲۵ ) + ( ۲ \times ۴۹ ) - ۱۶ }{ ۴ } }$$

$$m _ b = \sqrt { \frac { ۵۰ + ۹۸ - ۱۶ }{ ۴ } }$$

$$m _ b = \sqrt { \frac { ۱۳۲ }{ ۴ } }$$

$$m _ b = \sqrt { ۳۳ }$$

$$m _ b = ۵/۷۴$$

$$m _ c = \sqrt { \frac { ( ۲ \times ۵ ^ ۲ ) + ( ۲ \times ۴ ^ ۲ ) - ۷ ^ ۲ }{ ۴ } }$$

$$m _ c = \sqrt { \frac { ( ۲ \times ۲۵ ) + ( ۲ \times ۱۶ ) - ۴۹}{ ۴ } }$$

$$m _ c = \sqrt { \frac { ۵۰ + ۳۲ - ۴۹ }{ ۴ } }$$

$$m _ c = \sqrt { \frac { ۳۳ }{ ۴ } }$$

$$m _ c = \sqrt { ۸/۲۵ }$$

$$m _ c = ۲/۸۷$$

به این ترتیب، میانه نظیر ضلع AC برابر با ۵/۷۴ و میانه نظیر ضلع AB برابر با ۲/۸۷ است.

فرمول محاسبه طول ضلع مثلث بر اساس میانه

در بخش قبلی، فرمول‌های محاسبه میانه مثلث بر اساس ضلع را معرفی کردیم. اگر اندازه میانه‌ها را داشته باشیم، امکان محاسبه هر یک از ضلع‌های مثلث فراهم می‌شود. مثلث زیر را در نظر بگیرید.

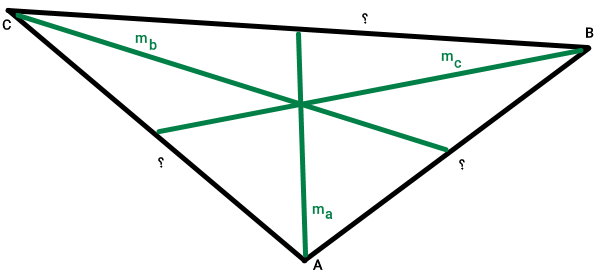
در مثلث بالا، طول میانه‌های مثلث، معلوم بوده و طول ضلع‌های آن مجهول است. برای به دست آوردن طول هر ضلع، می‌توانیم از فرمول‌های زیر استفاده کنیم:

$$a = \frac { ۲ } { ۳ } \sqrt { - m ^ ۲ _ a + ۲ m _ b ^ ۲ + ۲ m _ c ^ ۲ }$$

$$b = \frac { ۲ } { ۳ } \sqrt { - m ^ ۲ _ b + ۲ m _ a ^ ۲ + ۲ m _ c ^ ۲ }$$

$$c = \frac { ۲ } { ۳ } \sqrt { - m ^ ۲ _ c + ۲ m _ b ^ ۲ + ۲ m _ a ^ ۲ }$$

• a: طول ضلع BC
• b: طول ضلع AC
• c: طول ضلع AB

مثال ۲: محاسبه اندازه ضلع مثلث

اندازه میانه‌های یک مثلث مختلف‌الاضلاع برابر با ۴، ۵ و ۶ سانتی‌متر است. اندازه میانه نظیر بزرگ‌ترین ضلع مثلث را به دست بیاورید. برای درک بهتر سوال، ابتدا یک مثلث مختلف‌الاضلاع فرضی را به همراه میانه‌هایش رسم می‌کنیم.

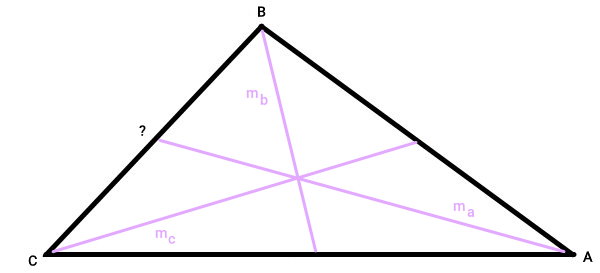
در مثلث بالا، داریم:

• m_a: میانه ضلع BC
• m_b: میانه ضلع AC
• m_c: میانه ضلع AB
• a: طول ضلع BC
• b: طول ضلع AC
• c: طول ضلع AB

اندازه‌های داده شده در صورت سوال را به صورت دلخواه به پارامترهای بالا اختصاص می‌دهیم:

• m_a: میانه ضلع BC برابر با ۴ سانتی‌متر
• m_b: میانه ضلع AC برابر با ۵ سانتی‌متر
• m_c: میانه ضلع AB برابر با ۶ سانتی‌متر

کوچک‌ترین میانه مثلث، به بزرگ‌ترین ضلع آن وارد می‌شود. بنابراین، سوال از ما، اندازه ضلع BC (مقدار a) را می‌خواهد. اندازه این ضلع برابر است با:

$$a = \frac { ۲ } { ۳ } \sqrt { - m ^ ۲ _ a + ۲ m _ b ^ ۲ + ۲ m _ c ^ ۲ }$$

$$a = \frac { ۲ } { ۳ } \sqrt { - ۴ ^ ۲ + ( ۲ \times ۵ ^ ۲ ) + ( ۲ \times ۶ ^ ۲ ) }$$

$$a = \frac { ۲ } { ۳ } \sqrt { - ۱۶ + ( ۲ \times ۲۵ ) + ( ۲ \times ۳۶ ) }$$

$$a = \frac { ۲ } { ۳ } \sqrt { - ۱۶ + ۵۰ + ۷۲ }$$

$$a = \frac { ۲ } { ۳ } \sqrt { ۱۰۶ }$$

$$a = \frac { ۲ \times ۱۰/۳ } { ۳ }$$

$$a = \frac { ۲۰/۶ } { ۳ }$$

$$a = ۶/۸۶$$

در نتیجه، اندازه بزرگ‌ترین ضلع مثلث برابر با ۶/۸۶ است.

مثال ۳: محاسبه مساحت مثلث از روی میانه

اندازه میانه‌های یک مثلث برابر با ۴، ۹ و ۱۰ سانتی‌متر است. مساحت مثلث را محاسبه کنید.

برای درک بهتر سوال، ابتدا یک مثلث فرضی را به همراه میانه‌هایش رسم می‌کنیم.

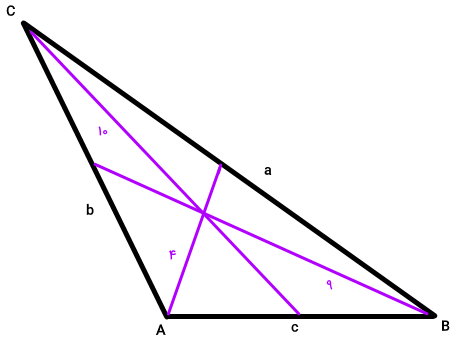
در مثلث بالا، داریم:

• m_a: میانه ضلع BC
• m_b: میانه ضلع AC
• m_c: میانه ضلع AB
• a: طول ضلع BC
• b: طول ضلع AC
• c: طول ضلع AB

اندازه‌های داده شده در صورت سوال را به صورت دلخواه به پارامترهای بالا اختصاص می‌دهیم:

• m_a: میانه ضلع BC برابر با ۴ سانتی‌متر
• m_b: میانه ضلع AC برابر با ۹ سانتی‌متر
• m_c: میانه ضلع AB برابر با ۱۰ سانتی‌متر

فرمول محاسبه ضلع مثلث از روی میانه‌های آن به صورت زیر نوشته می‌شود:

$$a = \frac { ۲ } { ۳ } \sqrt { - m ^ ۲ _ a + ۲ m _ b ^ ۲ + ۲ m _ c ^ ۲ }$$

$$a = \frac { ۲ } { ۳ } \sqrt { - ۴ ^ ۲ + ( ۲ \times ۹ ^ ۲ ) + ( ۲ \times ۱۰ ^ ۲ ) }$$

$$a = \frac { ۲ } { ۳ } \sqrt { - ۱۶ + ( ۲ \times ۸۱ ) + ( ۲ \times ۱۰۰ ) }$$

$$a = \frac { ۲ } { ۳ } \sqrt { - ۱۶ + ۱۶۲ + ۲۰۰ }$$

$$a = \frac { ۲ \times ۱۸/۶ } { ۳ }$$

$$a = \frac { ۳۷/۲ } { ۳ }$$

$$a = ۱۲/۴$$

به این ترتیب، طول یکی از ضلع‌ها را به دست آوردیم. اکنون به سراغ محاسبه ضلع بعدی می‌رویم:

$$b = \frac { ۲ } { ۳ } \sqrt { - m ^ ۲ _ b + ۲ m _ a ^ ۲ + ۲ m _ c ^ ۲ }$$

$$b = \frac { ۲ } { ۳ } \sqrt { - ۹ ^ ۲ + ( ۲ \times ۴ ^ ۲ ) + ( ۲ \times ۱۰ ^ ۲ ) }$$

$$b = \frac { ۲ } { ۳ } \sqrt { - ۸۱ + ( ۲ \times ۱۶ ) + ( ۲ \times ۱۰۰ ) }$$

$$b = \frac { ۲ } { ۳ } \sqrt { - ۸۱ + ۳۲ + ۲۰۰ }$$

$$b = \frac { ۲ } { ۳ } \sqrt { ۱۵۱ }$$

$$b = \frac { ۲ \times ۱۲/۲۹ } { ۳ }$$

$$b = \frac { ۲۴.۵۸ } { ۳ }$$

$$b = ۸/۱۹$$

برای ضلع سوم نیز داریم:

$$c = \frac { ۲ } { ۳ } \sqrt { - m ^ ۲ _ c + ۲ m _ b ^ ۲ + ۲ m _ a ^ ۲ }$$

$$c = \frac { ۲ } { ۳ } \sqrt { - ۱۰ ^ ۲ + ( ۲ \times ۴ ^ ۲ ) + ( ۲ \times ۹ ^ ۲ ) }$$

$$c = \frac { ۲ } { ۳ } \sqrt { - ۱۰۰ + ( ۲ \times ۱۶ ) + ( ۲ \times ۸۱ ) }$$

$$c = \frac { ۲ } { ۳ } \sqrt { - ۱۰۰ + ۳۲ + ۱۶۲ }$$

$$c = \frac { ۲ \times ۹/۶۹ } { ۳ }$$

$$c = \frac { ۱۹/۳۸ } { ۳ }$$

$$c = \frac { ۲ \times ۹/۶۹ } { ۳ }$$

$$c = ۶/۴۶$$

بنابراین، اندازه ضلع‌های مثلث به ترتیب برابر با ۱۲/۴، ۸/۱۹ و ۶/۴۶ سانتی‌متر است. اکنون، اندازه سه ضلع را داریم. این اندازه‌ها، امکان محاسبه مساحت مثلث را فراهم می‌کنند. فرمول محاسبه مساحت مثلث با سه ضلع معلوم (فرمول هرون) به صورت زیر نوشته می‌شود:

$$A = \sqrt { s ( s - a ) ( s - b ) ( s - c ) }$$

• A: مساحت
• s: نصف محیط مثلث
• a: طول ضلع اول برابر با ۱۲/۴۰ سانتی‌متر
• b: طول ضلع دوم برابر با ۸/۱۹ سانتی‌متر
• c: طول ضلع سوم برابر با ۶/۴۶ سانتی‌متر

فرمول محاسبه نصف محیط مثلث عبارت است از:

$$s = \frac { a + b + c } { ۲ }$$

$$s = \frac { ۱۲/۴۰ + ۸/۱۹ + ۶/۴۶ } { ۲ }$$

$$s = \frac { ۲۷/۰۵ } { ۲ }$$

$$s = ۱۳/۵۲$$

مقادیر معلوم را در فرمول مساحت قرار می‌دهیم:

$$A = \sqrt { ۱۳/۵۲ ( ۱۳/۵۲ - ۱۲/۴۰ ) ( ۱۳/۵۲ - ۸/۱۹ ) ( ۱۳/۵۲ - ۶/۴۶) }$$

$$A = \sqrt { ۱۳/۵۲ ( ۱/۱۲ ) ( ۵.۳۳ ) ( ۷.۰۶) }$$

$$A = \sqrt { ۵۶۹/۸۰ }$$

$$A = ۲۳/۸۷$$

در نتیجه، مساحت مثلث، تقریبا برابر با ۲۳/۸۷ سانتی‌متر مربع است.

محاسبه ضلع مثلث با اندازه میانه و دو ضلع دیگر

اگر طول دو ضلع مثلث را داشته باشیم، با دانستن طول هر یک از میانه‌ها می‌توانیم اندازه ضلع سوم را به دست بیاوریم.

فیلم آموزش هندسه پایه دهم – هندسه 1 در فرادرس

کلیک کنید

این کار با استفاده از فرمول‌های زیر انجام می‌گیرد:

$$a = \sqrt { ۲ ( b ^ ۲ + c ^ ۲ ) - ۴ m _ a ^ ۲ } = \sqrt { \frac { b ^ ۲ }{ ۲ } - c ^ ۲ + ۲ m _ b ^ ۲ } = \sqrt { \frac { c ^ ۲ }{ ۲ } - b ^ ۲ + ۲ m _ c ^ ۲ }$$

$$b = \sqrt { ۲ ( a ^ ۲ + c ^ ۲ ) - ۴ m _ b ^ ۲ } = \sqrt { \frac { a ^ ۲ }{ ۲ } - c ^ ۲ + ۲ m _ a ^ ۲ } = \sqrt { \frac { c ^ ۲ }{ ۲ } - a ^ ۲ + ۲ m _ c ^ ۲ }$$

$$c = \sqrt { ۲ ( b ^ ۲ + a ^ ۲ ) - ۴ m _ c ^ ۲ } = \sqrt { \frac { b ^ ۲ }{ ۲ } - a ^ ۲ + ۲ m _ b ^ ۲ } = \sqrt { \frac { a ^ ۲ }{ ۲ } - b ^ ۲ + ۲ m _ a ^ ۲ }$$

برای مثلث ABC، پارامترهای بالا عبارت هستند از:

• a: طول ضلع BC
• b: طول ضلع AC
• c: طول ضلع AB
• m_a: میانه ضلع BC
• m_b: میانه ضلع AC
• m_c: میانه ضلع AB

فرمول مساحت مثلث با میانه

در مثال ۳، نحوه محاسبه مساحت مثلث با استفاده از اندازه میانه‌ها را آموزش دادیم. در این مثال، ابتدا اندازه هر ضلع را به دست آوردیم. سپس، مساحت مثلث را به کمک فرمول هرون محاسبه کردیم. البته یک فرمول برای محاسبه مستقیم مساحت مثلث با میانه و بدون نیاز به اندازه ضلع‌ها وجود دارد. این فرمول عبارت است از:

$$A = \frac { ۴ }{ ۳ } \sqrt { \sigma ( \sigma - m _ a ) ( \sigma - m _ b ) ( \sigma - m _ c ) }$$

• A: مساحت مثلث
• σ: مجمع میانه‌ها تقسیم بر دو
• m_a: میانه ضلع اول
• m_b: میانه ضلع دوم
• m_c: میانه ضلع سوم

مثال ۴: محاسبه مساحت مثلث از روی میانه

مساحت مثلث معرفی شده در مثال ۳ را با استفاده مستقیم از اندازه میانه‌ها به دست بیاورید.

فرمول مساحت مثلث با میانه عبارت است از:

$$A = \frac { ۴ }{ ۳ } \sqrt { \sigma ( \sigma - m _ a ) ( \sigma - m _ b ) ( \sigma - m _ c ) }$$

• A: مساحت مثلث
• σ: مجمع میانه‌ها تقسیم بر دو
• m_a: میانه ضلع اول برابر با ۴ سانتی‌متر
• m_b: میانه ضلع دوم برابر با ۹ سانتی‌متر
• m_c: میانه ضلع سوم برابر با ۱۰ سانتی‌متر

σ، به صورت زیر محاسبه می‌شود:

$$\sigma = \frac { ۴ + ۹ + ۱۰ }{ ۲ }$$

$$\sigma = \frac { ۲۳ }{ ۲ }$$

$$\sigma = ۱۱/۵$$

مقادیر مشخص را درون فرمول مساحت قرار می‌دهیم:

$$A = \frac { ۴ }{ ۳ } \sqrt { \sigma ( \sigma - m _ a ) ( \sigma - m _ b ) ( \sigma - m _ c ) }$$

$$A = \frac { ۴ }{ ۳ } \sqrt { ۱۳/۵ ( ۱۳/۵ - ۴ ) ( ۱۳/۵ - ۹ ) ( ۱۳/۵ - ۱۰ ) }$$

$$A = \frac { ۴ }{ ۳ } \sqrt { ۱۳/۵ ( ۹/۵ ) ( ۴/۵ ) ( ۳/۵ ) }$$

$$A = \frac { ۴ }{ ۳ } \sqrt { ۲۰۱۹/۹۳۷۵ }$$

$$A = \frac { ۴ \times ۱۴۹/۶۲۵}{ ۳ }$$

$$A = \frac { ۱۷۹/۷۷ }{ ۳ }$$

$$A = ۵۹/۹۲$$

در نتیجه، مساحت مثلث تقریبا برابر با ۵۹/۹۲ سانتی‌متر مربع است. به دلیل تعداد محاسبات کمتر، استفاده از فرمول، خطای محاسبات را کاهش می‌دهد.

تفاوت ارتفاع و نیمساز با میانه مثلث چیست ؟

از دیگر اندازه‌های یک مثلث، می‌توان به ارتفاع و نیمساز آن اشاره کرد. ارتفاع، پاره‌خطی است که از راس مثلث به ضلع مقابل عمود می‌شود. هر مثلث، سه ارتفاع دارد. تصویر زیر، ارتفاع‌های یک مثلث منفرجه (مثلثی با یک زاویه بزرگ‌تر از ۹۰ درجه) را نمایش می‌دهد.

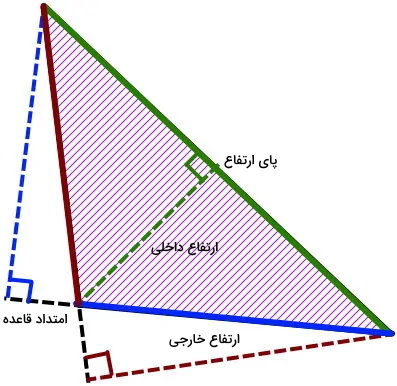
همان‌طور که مشاهده می‌کنید، برخلاف میانه، ارتفاع می‌تواند در خارج از محیط مثلث یا داخل آن قرار داشته باشد. در برخی از انواع مثلث‌های حاده (مثلث‌های دارای زاویه کوچکتر از ۹۰ درجه)، ارتفاع بر روی میانه منطبق می‌شود.

نیم‌ساز، پاره خطی است که یک زاویه را به دو زاویه برابر تقسیم می‌کند. در مثلث، به پاره‌خطی که زاویه راس را نصف کند، نیم‌ساز می‌گویند. تصویر زیر، نیم‌ساز یکی از راس‌های یک مثلث مختلف‌الاضلاع را نمایش می‌دهد.

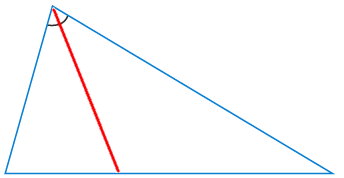
در برخی از مثلث‌های حاده، میانه بر روی نیم‌ساز منطبق می‌شود. در بخش‌های بعدی، به معرفی این مثلث‌ها خواهیم پرداخت.

میانه در انواع مثلث

در بخش‌های قبلی، مفهوم میانه در حالت کلی مثلث (مثلث مختلف الاضلاع) را مورد بررسی قرار دادیم. در این بخش، به معرفی میانه و خواص آن در دیگر انواع مثلث نظیر مثلث قائم‌الزاویه، متساوی‌الاضلاع و متساوی‌الساقین می‌پردازیم.

فیلم آموزش هندسه ۲ – پایه یازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

میانه در مثلث متساوی الاضلاع

مثلث متساوی‌الاضلاع، مثلثی با ضلع‌های برابر و سه زاویه داخلی ۶۰ درجه است. در این مثلث، میانه نظیر هر ضلع، بر روی ارتفاع نظیر آن ضلع منطبق می‌شود. علاوه بر این، هر میانه، زاویه را به دو زاویه مساوی (دو زاویه ۳۰ درجه) تقسیم می‌کند. به عبارت دیگر، میانه‌های مثلث متساوی الاضلاع، ارتفاع و نیم‌ساز این مثلث نیز هستند.

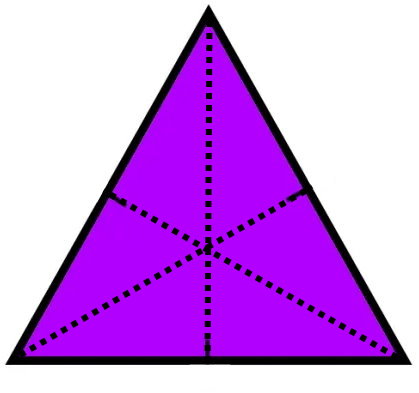
به دلیل یکسان بودن میانه و ارتفاع در مثلث متساوی‌الاضلاع، محاسبه آن با استفاده از فرمول‌های محاسبه ارتفاع نیز امکان‌پذیر است. به این ترتیب، فرمول میانه مثلث متساوی‌الاضلاع به صورت زیر نوشته می‌شود:

$$h = \frac { \sqrt { ۳ } } { ۲ } \times a$$

• h: اندازه ارتفاع و میانه مثلث متساوی‌الاضلاع
• a: اندازه ضلع مثلث متساوی‌الاضلاع

رابطه بین مساحت و میانه مثلث متساوی‌الاضلاع نیز عبارت است:

$$h =\frac { ۲ A } { b }$$

• h: اندازه ارتفاع و میانه مثلث متساوی‌الاضلاع
• A: مساحت مثلث
• b: ضلع نظیر میانه h

میانه در مثلث متساوی الساقین

مثلث متساوی‌الساقین، مثلثی با دو ضلع برابر است. به ضلع‌های هم‌اندازه این مثلث، ساق و به ضلع سوم، قاعده می‌گویند. در مثلث متساوی‌الساقین، میانه نظیر قاعده، بر روی ارتفاع نظیر قاعده قرار دارد. به عبارت دیگر، یکی از میانه‌های این مثلث، ارتفاع نیز هست. این میانه، راس نظیر خود را به دو زاویه برابر تقسیم می‌کند و به عنوان نیم‌ساز آن راس در نظر گرفته می‌شود. به عنوان مثال، تصویر زیر، یک مثلث متساوی‌الساقین را نمایش می‌دهد.

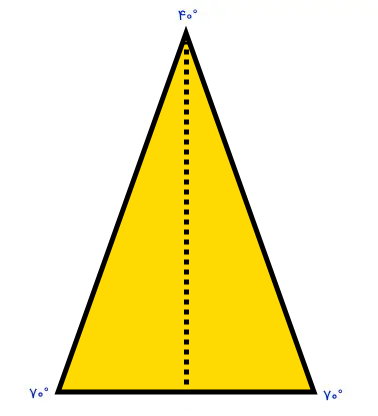
دو راس این مثلث، دارای زاویه مساوی بوده و دو ضلع آن دارای اندازه برابر هستند. پاره‌خطی که از راس سوم به مرکز ضلع سوم رسم شده، میانه مثلث است. این میانه، ارتفاع نظیر ضلع سوم و نیم‌ساز زاویه راس سوم نیز محسوب می‌شود. فرمول ارتفاع نظیر قاعده مثلث متساوی الساقین برابر است با:

$$\mathrm{h}_{\mathrm{b}}=\sqrt{\mathrm{a}^{۲}-(۰.۵ \times \mathrm{b})^{۲}}$$

• h_b: ارتفاع نظیر قاعده
• a: اندازه ساق

از فرمول بالا برای محاسبه میانه نظیر قاعده نیز استفاده می‌شود؛ چراکه این میانه بر روی ارتفاع نظیر قاعده منطبق است.

میانه در مثلث قائم الزاویه

مثلث قائم‌الزاویه، مثلثی با دو زاویه حاده (کوچکتر از ۹۰ درجه) و یک زاویه راست (زاویه ۹۰ درجه) است. ضلع‌های متصل به زاویه قائمه، با عنوان ساق و ضلع روبه‌روی این زاویه با عنوان وتر شناخته می‌شود. در حالت کلی، محاسبه میانه مثلث قائم‌الزاویه، تفاوتی با محاسبه میانه‌های مثلث مختلف‌الاضلاع ندارد. البته اگر اندازه ساق‌های این مثلث برابر باشد، یک مثلث متساوی‌الساقین قائم‌الزاویه به وجود می‌آید.

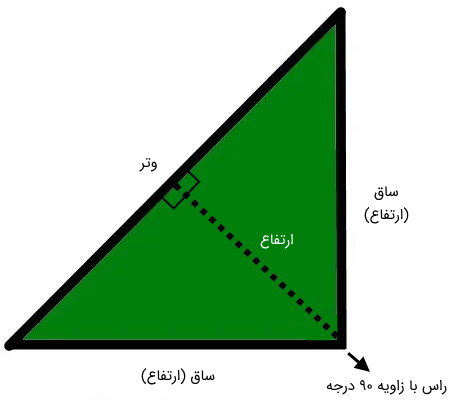
در صورت داشتن اندازه هر سه ضلع مثلث قائم‌الزاویه متساوی‌الساقین، می‌توانیم از فرمول زیر برای به دست آوردن میانه نظیر وتر استفاده کنیم:

$$h_c = \frac {a \times b} {c}$$

• h_c: ارتفاع نظیر وتر (میانه نظیر وتر)
• c: وتر
• a: یکی از ساق‌ها
• b: ساق دیگر

اگر فقط اندازه ساق را داشته باشیم، فرمول محاسبه میانه به صورت زیر نوشته می‌شود:

$$\mathrm{h}_{\mathrm{b}}= \frac {\sqrt {۲}} {۲} \times a$$

• h_b: ارتفاع نظیر وتر (میانه نظیر وتر)
• a: اندازه ساق

مثال ۵: محاسبه اندازه ضلع از روی میانه

میانه یک مثلث متساوی‌الاضلاع برابر با ۱۲ سانتی‌‌متر است. اندازه ضلع‌های آن را به دست بیاورید.

فیلم آموزش هندسه 3 – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

میانه مثلث متساوی‌الاضلاع با استفاده از رابطه زیر محاسبه می‌شود:

$$h = \frac { \sqrt { ۳ } } { ۲ } \times a$$

• h: اندازه ارتفاع و میانه مثلث متساوی‌الاضلاع برابر با ۱۲ سانتی‌متر
• a: اندازه ضلع مثلث متساوی‌الاضلاع

اندازه معلوم را در رابطه بالا قرار می‌دهیم:

$$۱۲ = \frac { \sqrt { ۳ } } { ۲ } \times a$$

$$۱۲ \times ۲ = \sqrt { ۳ } \times a$$

$$۲۴ = \sqrt { ۳ } \times a$$

$$a = \frac { ۲۴ } { \sqrt { ۳ } }$$

$$a = \frac { ۲۴ } { ۱/۷۳ }$$

$$a = ۱۳/۸۷$$

اثبات خواص میانه مثلث

در این بخش، به اثبات برخی از خواص میانه‌های مثلث می‌پردازیم. آشنایی با خواص مثلث، درک مراحل این اثبات‌ها را ساده‌تر می‌کند. برخی از خواص مهم مثلث که رابطه نزدیکی با خواص میانه‌ها دارند، عبارت هستند از:

• خط واصل مراکز دو ضلع مثلث، با ضلع سوم موازی است.
• خط واصل مراکز دو ضلع مثلث، نصف ضلع سوم است.
• اگر دو زاویه دو مثلث با هم برابر باشند، آن دو مثلث، متشابه‌اند.
• در مثلث‌های متشابه، نسبت ضلع‌های نظیر با هم برابر است.
• ضلع مقابل به بزرگ‌ترین زاویه داخلی مثلث، بزرگ‌ترین ضلع مثلث است.

اثبات فرمول طول میانه

مثلث ABC و میانه نظیر ضلع AC در این مثلث را در نظر بگیرید.

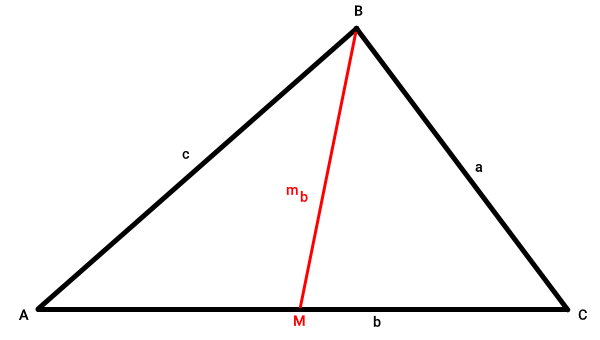
طول میانه BM در مثلث ABC، از فرمول زیر به دست می‌آید:

$$m _ b = \sqrt { \frac { ۲ a ^ ۲ + ۲ c ^ ۲ - b ^ ۲ }{ ۴ } }$$

میانه BM، در مقابل زاویه راس C قرار دارد.

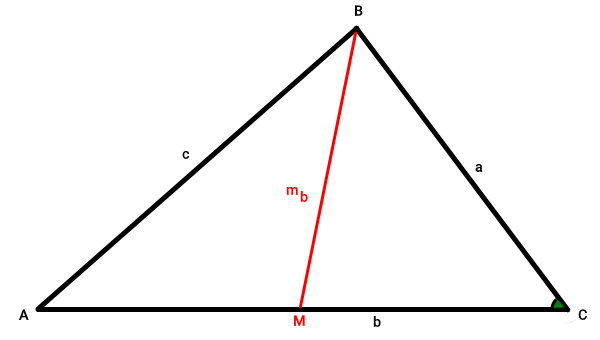
بر اساس قانون کسینوس‌ها، رابطه زیر بین زاویه C و ضلع‌های مثلث ABC برقرار است:

$$c ^ ۲ = a ^ ۲ + b ^ ۲ - ۲ a bcos C$$

رابطه بالا را بر حسب کسینوس زاویه C بازنویسی می‌کنیم:

$$\cos C = \frac { a ^ ۲ + b ^ ۲ - c ^ ۲ }{ ۲ a b }$$

مثلث MBC را در نظر بگیرید.

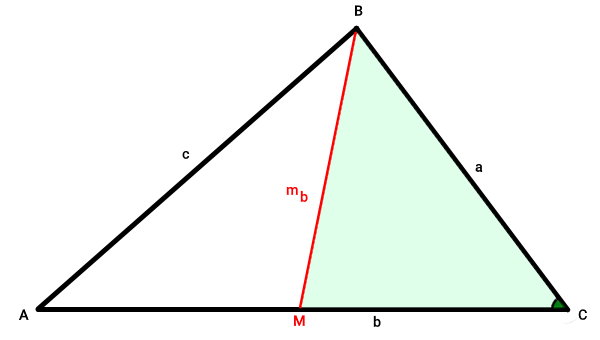
پاره‌خط BM (میانه نظیر AC)، ضلع AC را به قسمت مساوی (AM و MC) تقسیم می‌کند. بنابراین داریم:

$$M C = \frac { ۱ } { ۲ } A C = \frac { ۱ } { ۲ } b$$

اکنون، قانون کسینوس‌ها برای نمایش رابطه بین زاویه راس C و ضلع‌های مثلث MBC می‌نویسیم:

$$m _ b ^ ۲ = a ^ ۲ + \left ( \frac { ۱ }{ ۲ } b \right ) ^ ۲ - ۲ a .frac { ۱ } { ۲ } b \cos C$$

در قدم قبلی، رابطه کسینوس زاویه C را بر حسب اندازه ضلع‌های مثلث ABC به دست آوردیم. این رابطه را درون فرمول بالا قرار می‌دهیم:

$$m _ b ^ ۲ = a ^ ۲ + \left ( \frac { ۱ }{ ۲ } b \right ) ^ ۲ - ۲ a .frac { ۱ } { ۲ } b . \frac { a ^ ۲ + b ^ ۲ - c ^ ۲ }{ ۲ a b }$$

$$m _ b ^ ۲ = a ^ ۲ + \frac { b ^ ۲ }{ ۴ } - \frac { a ^ ۲ + b ^ ۲ - c ^ ۲ }{ ۲ }$$

از عبارت‌های سمت راست، مخرج مشترک می‌گیریم:

$$m _ b ^ ۲ = \frac { ۲ a ^ ۲ + ۲ c ^ ۲ - b ^ ۲ }{ ۴ }$$

با گرفتن جذر از دو طرف معادله، به رابطه زیر می‌رسیم:

$$m _ b = \sqrt { \frac { ۲ a ^ ۲ + ۲ c ^ ۲ - b ^ ۲ }{ ۴ } }$$

به این ترتیب، فرمول میانه مثلث اثبات می‌شود.

اثبات قضیه هم راسی میانه ها

میانه‌های مثلث، همدیگر یکدیگر را در یک نقطه مشترک قطع می‌کنند. این ویژگی، با عنوان «قضیه هم‌راسی میانه‌ها» شناخته می‌شود. برای اثبات این قضیه، مثلث ABC را در نظر بگیرد.

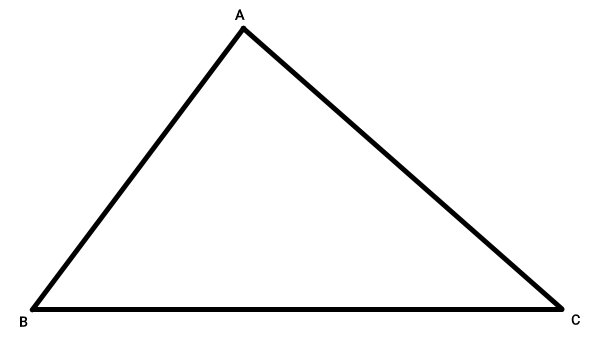
در مثلث ABC، میانه نظیر راس C، مرکز ضلع AB را در نقطه F قطع می‌کند. میانه نظیر راس B نیز ضلع AC را در نقطه E قطع می‌کند. محل تقاطع این میانه‌ها، نقطه G است.

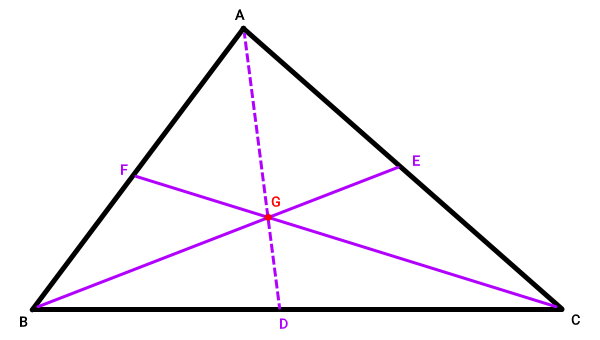
اگر میانه‌های مثلث، هم‌راس باشند، میانه نظیر راس A (پاره‌خط گذرنده از راس A و نقطه D در مرکز ضلع BC) نیز باید از نقطه G عبور کند. برای اثبات این ویژگی، ابتدا پاره‌خطی را از نقطه E‌ به F رسم می‌کنیم.

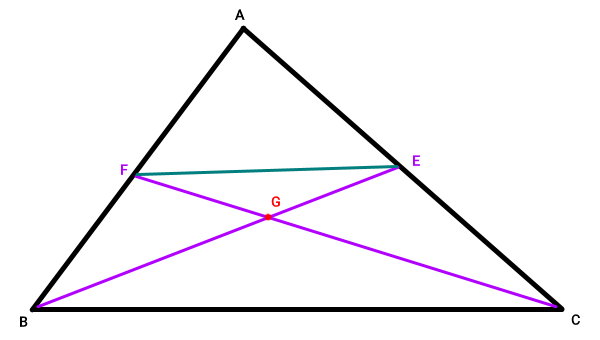
پاره‌خط EF، مراکز دو ضلع مثلث را به یکدیگر وصل می‌کند. بر اساس خواص مثلث، پاره‌خط اتصال‌دهنده مرکز دو ضلع، با ضلع سوم موازی است. بنابراین، EF با BC موازی است. اکنون، دو مثلث EFG و BCG را در نظر می‌گیریم.

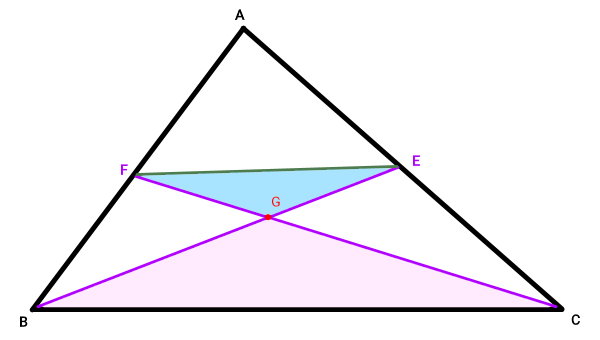
با توجه به قوانین جفت‌زاویه‌های خطوط موازی و متقاطع، زاویه EFG با زاویه GCB‌ و زاویه GEF با زاویه GBC برابر است. از طرفی، زاویه‌های FGE و BGC، متقابل به راس و برابر هستند. به دلیل برابر بودن تمام زاویه‌ها، دوم مثلث EFG و BCG، تشابه دارند. بنابراین، ضلع‌های آن‌ها با یکدیگر متناسب هستند. مطابق با خواص مثلث و قوانین تشابه مثلث‌ها، می‌توانیم نتیجه بگیریم که پاره‌خط EF، یک‌دوم، ضلع موازی با آن (ضلع BC) است. به این ترتیب، داریم:

$$\frac { E G }{ G B } = \frac { F E }{ B C } = \frac { ۱ }{ ۲ }$$

بر اساس روابط بالا می‌توانیم بگوییم که ضلع GB، دو برابر ضلع EG است:

$$۲ E G = G B$$

به عبارت دیگر، ضلع EG، یک‌سوم ضلع EB است:

$$B G = \frac { ۲ }{ ۳ } E B$$

در میانه دیگر نیز داریم:

$$C G = \frac { ۲ }{ ۳ } C F$$

به این ترتیب می‌توانیم بگوییم که میانه CF، میانه BE را دقیقا در دو-سوم فاصله B تا E قطع می‌کند. میانه BE نیز میانه CF را دقیقا در دو-سوم فاصله C تا F قطع می‌کند. بنابراین، در صورت تعیین مرکز ضلع CB (نقطه D) و رسم میانه سوم مثلث از راس A تا نقطه D، این میانه نیز باید دو میانه دیگر را در دو-سوم فاصله B تا E و دو-سوم فاصله C تا F قطع کند. به عبارت دیگر، میانه AD نیز باید از نقطه G عبور کند. برای اثبات این موضوع، یک پاره‌خط از نقطه مرکزی E به نقطه مرکزی D می‌کشیم.

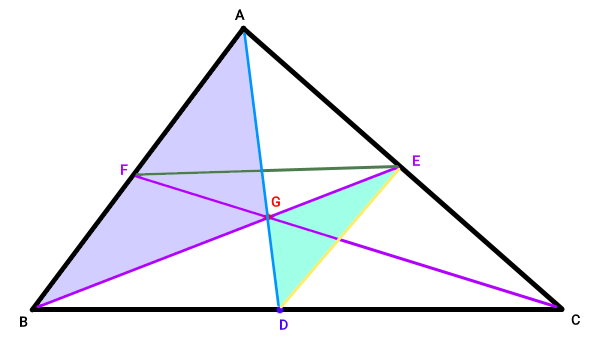
با توجه به خواص مثلث، قوانین جفت‌زاویه‌های خطوط موازی و زوایه‌های متقابل به راس، مثلث‌های DEG و ABG، دارای تشابه هستند. بنابراین داریم:

$$\frac { D G }{ G A } = \frac { E D }{ A B } = \frac { ۱ }{ ۲ }$$

$$۲ D G = G A$$

$$D G = \frac { ۲ }{ ۳ } A D$$

در نتیجه، میانه‌های AD و BE نیز یکدیگر را در دو-سوم فاصله راس تا مرکز ضلع (نقطه G) قطع می‌کنند. به عبارت دیگر، میانه‌های مثلث، هم‌راس هستند.

اثبات برابر بودن مساحت مثلث های ایجاد شده توسط میانه

میانه، مثلث را به دو مثلث کوچک‌تر با مساحت‌های برابر تقسیم می‌کند. برای اثبات این ویژگی، مثلث ABC را در نظر بگیرد. در این مثلث، میانه ضلع AC را از راس B رسم می‌کنیم. پاره‌خط BM در تصویر زیر، این میانه را نمایش می‌دهد.

با رسم میانه BM، مثلث ABC به دو مثلث AMB و CMB تقسیم می‌شود. برای به دست آوردن مساحت این مثلث‌ها، از فرمول زیر استفاده می‌کنیم:

۲ ÷ (قاعده × ارتفاع) = مساحت مثلث

ارتفاع مثلث ABC، پاره‌خط BH است که در نقطه H بر ضلع AC عمود می‌شود.

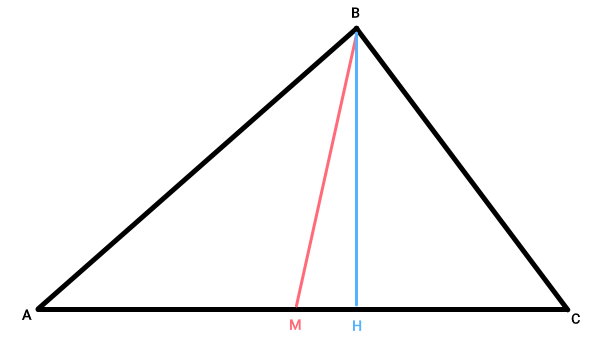
مساحت مثلث ABC برابر است با:

$$A _ { A B C } = \frac { ۱ } { ۲ } B H . A C$$

مثلث CMB را در نظر بگیرید. پاره‌خط BH، بر قاعده MC در این مثلث عمود است.

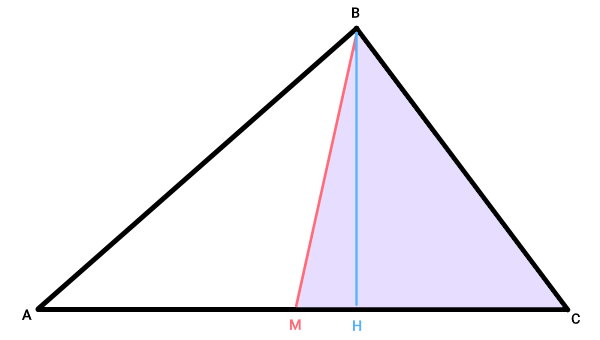
بنابراین می‌توان آن را به عنوان ارتفاع CMB در نظر گرفت. به این ترتیب، مساحت مثلث CMB از رابطه زیر به دست می‌آید:

$$A _ { C M B } = \frac { ۱ } { ۲ } B H . M C$$

اکنون، مثلث AMB را در نظر بگیرید. پاره‌خط BH، بر امتداد قاعده AM در این مثلث عمود می‌شود.

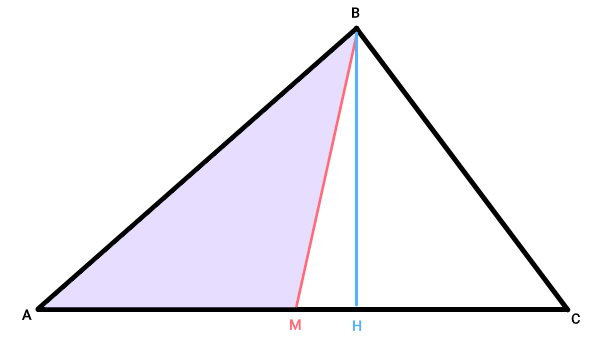
به همین دلیل، می‌توان آن را به عنوان ارتفاع AMB در نظر گرفت. به این ترتیب، مساحت مثلث AMB از رابطه زیر به دست می‌آید:

$$A _ { A M B } = \frac { ۱ } { ۲ } B H . A M$$

نقطه M، در مرکز ضلع AC قرار دارد. بنابراین:

$$A M = M C = \frac { ۱ } { ۲ } A C$$

در نتیجه، مساحت مثلث‌های AMB و CMB با یکدیگر برابر بوده و نصف مساحت مثلث ABC است.

اثبات کوچک تر بودن میانه نظیر بزرگ ترین ضلع مثلث

بزرگ‌ترین ضلع مثلث، کوچک‌ترین میانه را داشته و کوچک‌ترین ضلع مثلث، بزرگ‌ترین میانه را دارد. برای اثبات این ویژگی، مثلث ABC‌ را در نظر بگیرید.

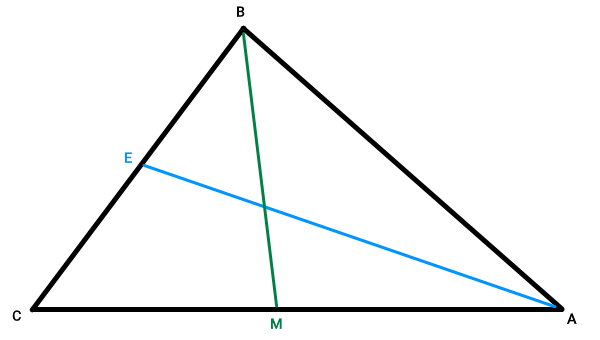
پاره‌خط‌های BM و AE، میانه‌های مثلث ABC‌ هستند. اگر ضلع AC، بلندتر از ضلع BC باشد، اثبات می‌کنیم که میانه BM (میانه نظیر ضلع AC)، کوچک‌تر از میانه AE (میانه نظیر ضلع BC) است. به عبارت دیگر:

اگر

$$A C \gt B C$$

بنابراین

$$B M \le A E$$

برای شروع اثبات گزاره‌های بالا، میانه سوم مثلث را رسم می‌کنیم و آن را CK می‌نامیم. در بخش‌های قبلی اثبات کردیم که میانه‌های مثلث، از یک نقطه مشترک عبور می‌کنند. این نقطه را با حرف O نمایش می‌دهیم.

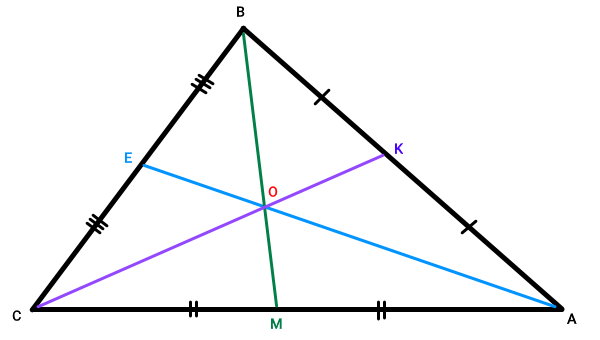
با رسم میانه‌ها، مثلث به چندین مثل کوچک‌تر تبدیل می‌شود. مثلث‌های CKA و CKB را در نظر بگیرید.

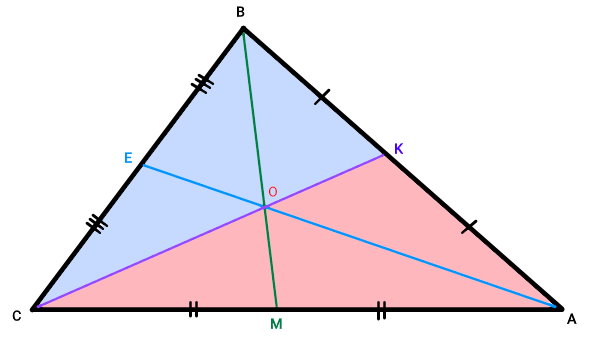
CK، ضلع مشترک میان این دو مثلث است. با توجه به فرضیات اتخاذ شده برای مثلث ABC، می‌دانیم:

$$A C \gt B C$$

بنابراین، ضلع AC در مثلث CKA بزرگ‌تر از ضلع BC در مثلث CKB است. بر اساس خواص مثلث‌ها، بزرگ‌ترین ضلع مثلث، روبه‌روی بزرگ‌ترین زاویه داخلی آن قرار می‌گیرد. بنابراین:

$$\angle A K C \gt \angle C K B$$

اکنون مثلث‌های AKO و OKB را در نظر بگیرید. OK، ضلع مشترک بین این دو مثلث است.

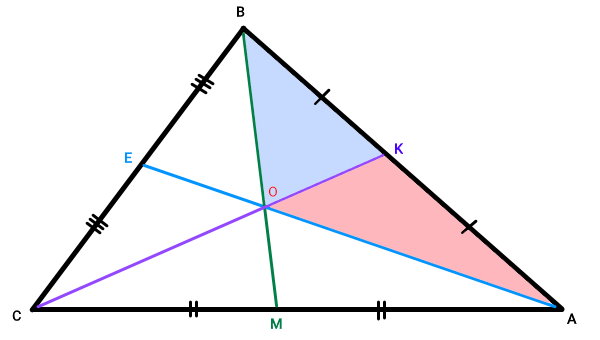
پار‌ه‌خط CK، میانه نظیر ضلع AB است. بنابراین، این ضلع را به دو قسمت مساوی تقسیم می‌کند:

$$A K = K B$$

در مرحله قبل، دیدیم که:

$$\angle A K C \gt \angle C K B$$

به دلیل بزرگ‌تر بودن زاویه AKC از زاویه CKB، ضلع AO (ضلع مقابل به زاویه AKC)، بزرگ‌تر از ضلع OB (ضلع مقابل به زاویه CKB) است:

$$A O \gt O B$$

با توجه به اثبات‌های قبلی، می‌ٰدانیم که میانه‌های مثلث همدیگر را با نسبت دو به یک (از راس تا مرکز ضلع نظیر) قطع می‌کنند. به این ترتیب، داریم:

$$A O = \frac { ۲ }{ ۳ } A E$$

$$B O = \frac { ۲ }{ ۳ } B M$$

می‌‌دانیم که ضلع AO از ضلع BO بزرگ‌تر است. بنابراین:

$$A O \gt B O \to \frac { ۲ }{ ۳ } A E \gt \frac { ۲ }{ ۳ } B M$$

در نتیجه:

$$A E \gt B M$$

به این ترتیب، اثبات کردیم که میانه نظیر ضلع کوچک‌تر، بزرگ‌تر از میانه نظیر ضلع بزرگ‌تر است.

سوالات متداول در رابطه با میانه مثلث

در این بخش، به برخی از پرتکرارترین سوالات مرتبط با مبحث میانه در مثلث به طور مختصر پاسخ می‌دهیم.

تعریف میانه مثلث چیست؟

میانه مثلث، پاره‌خط واصل یک راس مثلث به مرکز ضلع مقابل آن راس است.

هر مثلث چند میانه دارد ؟

هر مثلث، سه میانه دارد.

محل تلاقی سه میانه مثلث کجاست ؟

محل تلاقی سه میانه مثلث، مرکز ثقل یا مرکز مثلث است.

آیا میانه بر ضلع مثلث عمود است ؟

میانه، فقط در مثلث‌های متساوی‌الاضلاع و متساوی‌الساقین می‌تواند بر ضلع عمود باشد. بنابراین، میانه همیشه بر ضلع عمود نیست.

میانه چه تفاوتی با ارتفاع دارد ؟

ارتفاع، پاره‌خطی است که از یک راس مثلث به ضلع مقابل آن راس عمود می‌شود. میانه، لزوما بر ضلع نظیر خود عمود نیست. به علاوه، ارتفاع می‌تواند داخلی یا خارجی باشد اما میانه، فقط در داخل مثلث قرار می‌گیرد.

میانه چه تفاوتی با نیمساز دارد ؟

نیم‌ساز، پاره‌خطی است که زاویه راس را به دو زاویه برابر تقسیم می‌کند. میانه، لزوما نیم‌ساز راس نیست. البته در مثلث متساوی‌الاضلاع و متساوی‌الساقین، میانه می‌تواند نیم‌ساز نیز باشد.

میانه، ارتفاع و نیم‌ساز کدام مثلث یکسان است ؟

در مثلث متساوی‌الاضلاع، میانه، ارتفاع و نیم‌ساز، بر روی یکدیگر منطبق می‌شوند.

بزرگترین میانه مثلث کدام است ؟

میانه نظیر کوچک‌ترین ضلع مثلث، بزرگ‌ترین میانه مثلث است.

رابطه بین میانه و مساحت مثلث چیست ؟

میانه، مثلث را به دو مثلث با مساحت مساوی تقسیم می‌کند. به عبارت دیگر، میانه، مثلث را نصف می‌کند.