فرمول سرعت ثابت – نحوه محاسبه با مثال و تمرین

در مطالعه و بررسی مسائل فیزیک مکانیک، احتمالا با عبارت سرعت ثابت یا سرعت یکنواخت روبه‌رو شده‌اید. اگر در یک بازه زمانی مشخص، سرعت جسم در حال حرکتی چه از نظر اندازه و چه از نظر جهت تغییر نکند، در این صورت می‌گوییم حرکت جسم در این بازه زمانی حرکت با سرعت ثابت بوده است. فرمول سرعت ثابت، همان معادله حرکت جسم در این شرایط به‌صورت $$x=vt+x_0$$ است که نشان می‌دهد مکان جسم با گذشت زمان چگونه تغییر می‌کند.

در این نوشته از مجله فرادرس، پس از اینکه مفهوم و فرمول سرعت ثابت را کاملا توضیح دادیم، به بررسی کاربردهای این فرمول در حل مسائل مختلف می‌پردازیم. همچنین یاد می‌گیریم که نمودارهای مکان - زمان و سرعت - زمان در حرکت با سرعت ثابت چه شکلی دارند و به ما چه اطلاعاتی می‌دهند.

فرمول سرعت ثابت

حرکت با سرعت ثابت، ساده‌ترین نوع حرکت یک جسم است و زمانی اتفاق می‌افتد که اندازه و جهت سرعت جسم در حال حرکت در محدوده زمانی موردنظر ما برای بررسی حرکت، تغییری نکرده باشد.

در فرمول‌های سینماتیک برای توصیف این نوع حرکت، دو فرمول داریم که با عنوان فرمول سرعت ثابت در جدول زیر آورده شده‌اند:

در ادامه نحوه به‌دست آوردن این دو فرمول و ارتباط آن‌ها با حرکت سرعت ثابت را توضیح می‌دهیم. سپس به توضیح انواع نمودارهای حرکت می‌پردازیم تا با انواع مسائل این حوزه کاملا آشنا شوید.

فرمول سرعت متوسط

زمانی که از ثابت ماندن سرعت صحبت می‌کنیم، در واقع منظور ما تغییر نکردن مقدار و جهت سرعت لحظه‌ای در هر لحظه از زمان است. از طرفی سرعت متوسط معادل است با میانگین مقادیر سرعت لحظه‌ای در یک بازه زمانی. در حرکت با سرعت ثابت، هر بازه زمانی که برای محاسبه سرعت متوسط در نظر بگیریم، به ما نتیجه یکسانی خواهد داد. در واقع، برابر بودن سرعت لحظه‌ای در تمام نقاط، منجر به ایجاد سرعت متوسطی می‌شود که با هر یک از این مقادیر برابر است.

بنابراین در حرکت با سرعت ثابت داریم:

سرعت لحظه‌ای = سرعت متوسط = سرعت ثابت (یکنواخت)

اگر بخواهیم از منظر ثابت ماندن سرعت لحظه‌ای به نمودار مکان - زمان نگاه کنیم، می‌دانیم سرعت لحظه‌ای برابر است با شیب خط مماس بر نمودار مکان - زمان در هر لحظه. بنابراین اگر در بازه زمانی مشخصی حرکت با سرعت ثابت داشته باشیم، باید شیب تمام خط‌های مماس بر نمودار مکان - زمان در هر لحظه از این بازه یکسان باشند.

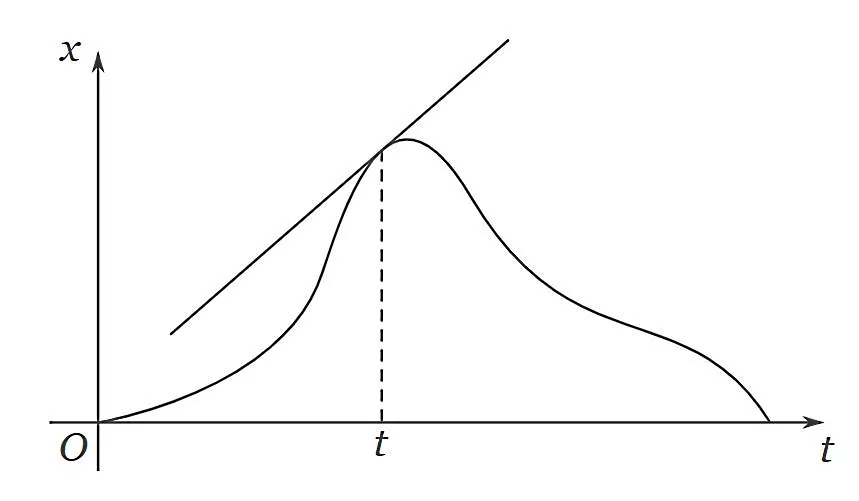
برای مثال اگر نمودار مکان - زمانی به شکل بالا داشته باشیم و سرعت لحظه‌ای را روی هر نقطه از آن رسم کنیم، هیچ بازه‌ای که در آن شیب خط‌های مماس بر نمودار مانند هم باشند، وجود ندارد. چنین نموداری توصیف کننده حرکت با سرعت ثابت نیست، بلکه سرعت متغیر و حرکت شتابدار را نشان می‌دهد.

اما اگر نمودار مکان - زمان ما به‌صورت زیر باشد، واضح است که اولا برای تمام زمان‌ها خط‌های مماس یکسانی کاملا منطبق بر نمودار داریم، ثانیا شیب تمام این خطوط مساوی با شیب نمودار است. پس نمودارهایی به شکل خط راست و نه منحنی، می‌توانند توصیف‌کننده حرکت سرعت ثابت باشند.

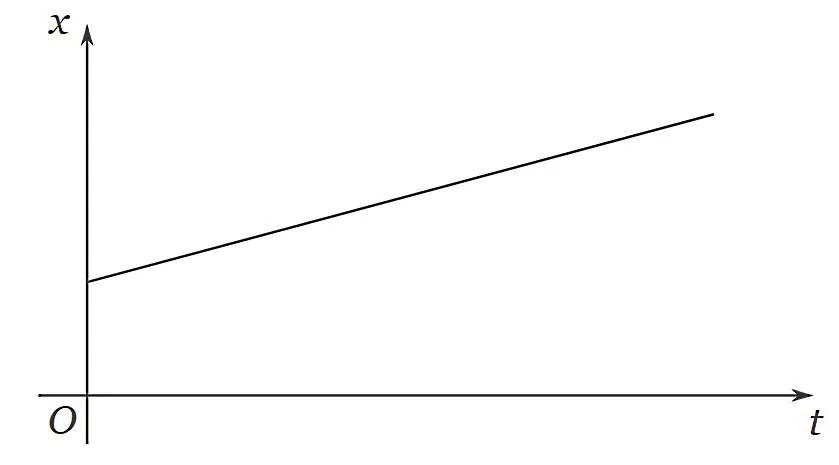
با توجه به شکل بالا می‌توانیم نتیجه‌گیری کنیم که شیب نمودار مکان بر حسب زمان، همان سرعت متوسط یا سرعت ثابت است و اگر شیب را به‌دست آوریم، سرعت متوسط را خواهیم داشت. برای محاسبه شیب نمودار بالا کافی است یک بازه زمانی مانند $$t_1$$ تا $$t_2$$ را در نظر بگیریم و مکان‌های متناظر با این لحظات را روی محور عمودی مشخص کنیم. به این ترتیب مثلث قائم‌الزاویه‌ای مطابق شکل زیر تشکیل می‌شود که شیب وتر آن برابر است با نسبت تغییرات مکانی به تغییرات زمانی. بنابراین فرمول سرعت متوسط می‌شود:

$$v=\frac{\triangle x}{\triangle t}=\frac{x_2-x_1}{t_2-t_1}$$

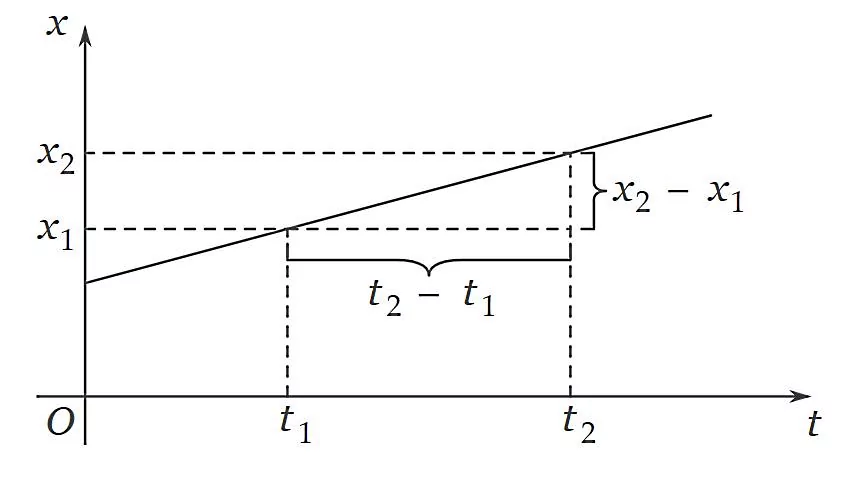
سرعتی که در فرمول اصلی حرکت با سرعت ثابت یعنی معادله مکان - زمان بکار می‌رود نیز همین سرعت است. اگر $$t_2-t_1$$ را $$t$$ در نظر بگیریم، معادله مکان - زمان به‌دست می‌آید:

$$\Rightarrow x_2-x_1=v(t_2-t_1)$$

$$\Rightarrow x_2=vt+x_1$$

در بخش بعد محاسبه معادله مکان - زمان را به شیوه دیگری توضیح می‌دهیم.

معادله مکان - زمان

پیش از پرداختن به اصلی‌ترین فرمول سرعت ثابت، در این بخش قصد داریم فیلم آموزشی فیزیک پایه دوازدهم – نکته و حل تست کنکور فرادرس را به شما معرفی کنیم که شامل حل سوالات چهار گزینه‌ای جهت آمادگی در کنکور سراسری در زمینه سرعت ثابت و فرمول‌های آن است. در ادامه لینک این دوره را برای شما قرار داده‌ایم:

استخراج معادله مکان - زمان، مستلزم تسلط به معادله یک خط مستقیم است. فرض کنید اتومبیلی از مکان و زمان صفر با سرعت صفر شروع به حرکت می‌کند و سرعت و مکان‌ آن در چهار لحظه بعدی، طبق جدول زیر اندازه‌گیری شده است:

همان‌طور که از جدول بالا مشخص است، سرعت اتومبیل در هر چهار زمان به شکل $$\vec{v}$$ اندازه‌گیری شده است. دقت کنید چون علامت بردار روی $$v$$ قرار دارد، پس هم جهت و هم اندازه سرعت در نظر گرفته شده‌ا‌ند. پس می‌توانیم بگوییم حرکت این اتومبیل در این محدوده زمانی، یک حرکت با سرعت ثابت محسوب می‌شود.

حالا اگر در صفحه مختصات، مکان این جسم را روی محور قائم یا y و زمان را روی محور افقی یا x در نظر بگیریم، در این صورت با رسم مکان بر حسب زمان، نمودار مکان - زمان حرکت این حرکت را ترسیم کرده‌ایم. به ازای هر زمانی مانند $$t_0$$، مکان اتومبیل با $$s_0$$ متناظر است. پس می‌توانیم پنج نقطه با مختصاتی به شکل زیر داشته باشیم:

1. $$(0, 0)$$
2. $$(t_0, s_0)$$
3. $$(t_1, s_1)$$
4. $$(t_2, s_2)$$
5. $$(t_3, s_3)$$

با اتصال این پنج نقطه به هم، طبق شکل زیر یک خط راست خواهیم داشت که همان نمودار مکان - زمان جسم است:

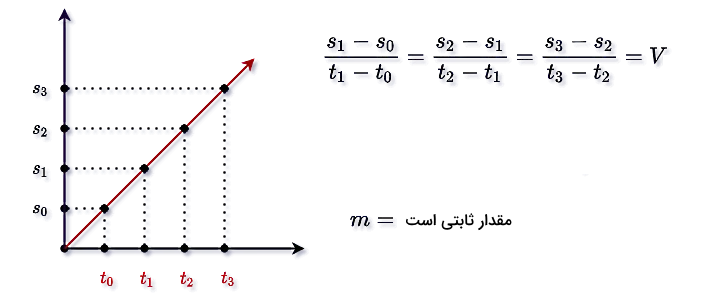
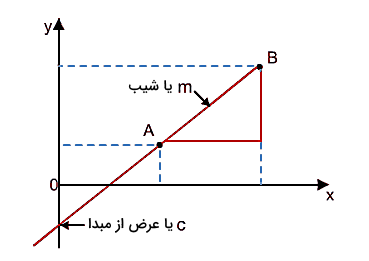
از ریاضیات می‌دانیم اگر با رسم نمودار $$y$$ بر حسب $$x$$، خط مستقیمی حاصل شود، معادله این خط به شکل زیر است:

$$y=mx+c$$

در این معادله، $$m$$ شیب خط و $$c$$ عرض از مبدا خط هستند. در مثال بالا، نمودار مکان - زمان ما به‌صورت $$s$$ بر حسب $$t$$ رسم شده است. پس این نمودار دارای معادله خطی به شکل زیر خواهد بود:

$$y=mx+c \Rightarrow s=mt+s_0$$

که در آن $$s_0$$ به‌عنوان عرض از مبدا معادل است با مکان اولیه اتومبیل. چون طبق فرض، مکان اولیه متحرک صفر در نظر گرفته شده است، پس داریم:

$$\Rightarrow s=mt$$

از طرفی، اگر دقت کنید در شکل بالا سه بازه زمانی داریم که برای هر کدام سرعت متوسط طبق فرمولی که توضیح دادیم، محاسبه می‌شود:

$$\vec{v}=\frac{\triangle \vec{s}}{\triangle t}$$

$$\Rightarrow \vec{v}=\frac{\triangle \vec{s}}{\triangle t}=\frac{\vec{s_1}-\vec{s_0}}{t_1-t_0}$$

$$\Rightarrow \vec{v}=\frac{\triangle \vec{s}}{\triangle t}=\frac{\vec{s_2}-\vec{s_1}}{t_2-t_1}$$

$$\Rightarrow \vec{v}=\frac{\triangle \vec{s}}{\triangle t}=\frac{\vec{s_3}-\vec{s_2}}{t_3-t_2}$$

اگر به روند فرمول‌های بالا دقت کنیم، نتبجه زیر حاصل می‌شود:

$$\Rightarrow \vec{v}=\frac{ \vec{s}}{t}$$

می‌توانیم برای راحتی، از علائم برداری صرف‌نظر کنیم:

$$\Rightarrow s=vt$$

از مقایسه عبارت‌های بالا، نتیجه می‌گیریم که شیب نمودار مکان - زمان در حرکت با سرعت ثابت با اندازه سرعت ثابت برابر است:

$$\begin{cases}s=vt \\s=mt \end{cases} \Rightarrow v=m$$

در ادامه با حل مثال خواهیم دید که از این نتیجه چگونه در حل مسائل حرکت با سرعت ثابت استفاده می‌شود. با جای‌گذاری سرعت به‌جای m در معادله خط، خواهیم داشت:

$$\Rightarrow s=vt+s_0$$

همچنین می‌توانیم مکان را به‌جای $$s$$ با $$x$$ نشان دهیم، در این صورت معادله خط راست که همان نمودار مکان - زمان حرکت اتومبیل با سرعت ثابت است، به شکل زیر می‌شود:

$$x=vt+x_0$$

• $$x_0$$: مکان اولیه برحسب متر ($$m$$)
• $$x$$: مکان نهایی برحسب متر ($$m$$)
• $$t$$: بازه زمانی جابجایی بر حسب ثانیه ($$t$$)
• $$v$$: سرعت ثابت بر حسب متر بر ثانیه ($$\frac{m}{s}$$)

پس در این قسمت یاد گرفتیم معادله مکان - زمان در حرکت با سرعت ثابت چگونه از معادله یک خط راست به‌دست می‌آید. اگر بخواهیم ببینیم انرژی ذخیره شده در جسمی که در حال حرکت با سرعت ثابتی است، چقدر است، باید از فرمول انرژی جنبشی به شکل $$K=\frac{1}{2}mv^2$$ استفاده کنیم. جهت حل مثال‌ و تمرین در این زمینه، می‌توانید مطلب «فرمول انرژی جنبشی چیست؟ – به زبان ساده با مثال و تمرین» از مجله فرادرس را مطالعه کنید.

قانون دوم نیوتن و فرمول سرعت ثابت

در این بخش می‌خواهیم ببینیم از منظر قانون دوم نیوتن، حرکت با سرعت ثابت چگونه ایجاد می‌شود و فرمول آن چیست. موضوع قانون دوم نیوتن این است: اگر سرعت جسم در حال حرکتی تغییر کند، جسم شتابی به‌دست خواهد آورد که با نیروی وارد بر آن نسبت مستقیم و با جرم آن نسبت عکس دارد. اگر بخواهیم این تعریف را در قالب ریاضیات نشان دهیم، به فرمول زیر می‌رسیم:

$$\sum \vec{F}=m \vec{a}$$

در این فرمول $$\sum \vec{F}$$ معادل است با مجموع نیروها یا برآیند تمام نیروهای وارد بر جسم که از طریق جمع برداری نیروها به‌دست می‌آید و با نیوتن ($$N$$) اندازه‌گیری می‌شود. همچنین $$m$$ جرم جسم بر حسب کیلوگرم ($$kg$$)‌ و $$\vec{a}$$ بر حسب متر بر مجذور ثانیه ($$\frac{m}{s^2}$$) شتابی است که جسم در این حرکت کسب کرده است. از طرفی می‌دانیم اگر جسمی در لحظه $$t_1$$ دارای سرعت $$\vec{v_1}$$ و در لحظه $$t_2$$ دارای سرعت $$\vec{v_2}$$ باشد، در این صورت چون با گذشت زمان سرعت تغییر کرده است، پس شتابی داریم که برابر است با:

$$\vec{a}=\frac{\triangle \vec{v}}{\triangle t}=\frac{\vec{v_2}-\vec{v_1}}{t_2-t_1}$$

با در نظر گرفتن فرمول شتاب به شکل بالا، فرمول قانون دوم نیوتن می‌شود:

$$\sum \vec{F}=m \vec{a} \Rightarrow \sum \vec{F}=m \ (\frac{\vec{v_2}-\vec{v_1}}{t_2-t_1})$$

گفتیم در حرکت با سرعت ثابت، اصل بر این است که سرعت تغییر نمی‌کند، یعنی داریم $$\vec{v_1}=\vec{v_2}$$. دقت کنید در فرمول‌های بالا سرعت، شتاب و نیرو کمیت‌های برداری هستند، به همین دلیل علامت پیکان در بالای هر یک از این کمیت‌ها قرار دارد، اما جرم و زمان کمیت‌ عددی محسوب می‌شوند. پس اگر در حرکت با سرعت ثابت باشیم، صورت کسر بالا صفر می‌شود:

$$\vec{v_1}=\vec{v_2} \Rightarrow \sum \vec{a}=0 \Rightarrow \sum \vec{F}=0$$

بنابراین طبق قانون دوم نیوتن، می‌توانیم دو نتیجه‌گیری زیر را در مورد حرکت با سرعت ثابت داشته باشیم که در واقع با هم معادل هستند:

• حرکت با سرعت ثابت حرکتی است که در آن مجموع نیروهای وارد بر جسم صفر است.
• حرکت با سرعت ثابت حرکتی است که در آن هیچ نیرویی به جسم وارد نمی‌شود.

همچنین فرمول سرعت ثابت بر اساس قانون دوم نیوتن به شکل زیر است:

$$\vec{v_1}=\vec{v_2} \Rightarrow \sum \vec{F}=0$$

چگونه فرمول سرعت ثابت را با فرادرس بهتر یاد بگیریم؟

در بخش قبل آموختیم فرمول سرعت ثابت چیست و در ادامه با نحوه استفاده از این فرمول‌ها نیز آشنا خواهید شد. اما پیش از آن، در این قسمت می‌خواهیم چند فیلم آموزشی تهیه شده در مجموعه فرادرس را به شما معرفی کنیم تا با مشاهده آن‌ها یادگیری عمیق‌تری از مبحث حرکت‌شناسی در فیزیک کسب کنید. با مراجعه به این دوره‌ها، به‌ویژه در فیلم‌های آموزشی مربوط به کتاب درسی علوم نهم و فیزیک دوازدهم از مقطع متوسطه، می‌توانید کاملا به مبحث انواع حرکت، فرمول سرعت ثابت و فرمول‌های حرکت با سرعت متغیر یا همان حرکت با شتاب ثابت مسلط شوید:

1. فیلم آموزش علوم تجربی نهم بخش فیزیک فرادرس
2. فیلم آموزش فیزیک دهم فرادرس
3. فیلم آموزش فیزیک دهم مرور و حل تمرین فرادرس
4. فیلم آموزش فیزیک دوازدهم فرادرس
5. فیلم آموزش فیزیک دوازدهم سوالات امتحانات نهایی با حل تشریحی فرادرس
6. فیلم آموزش فیزیک دوازدهم مرور و حل تمرین فرادرس
7. فیلم آموزش فیزیک دوازدهم نکته و حل تست کنکور فرادرس
8. فیلم آموزش رایگان دینامیک و حرکت دایره ای فرادرس
9. فیلم آموزش رایگان نمودار سرعت زمان در فیزیک فرادرس
10. فیلم آموزش رایگان معادله خط و ترسیم آن در هندسه فرادرس

مفهوم حرکت با سرعت ثابت

پیش از اینکه فرمول سرعت ثابت را توضیح دهیم، در این بخش به بررسی مفهوم سرعت ثابت می‌پردازیم. بررسی حرکت اجسام بدون در نظر گرفتن عامل ایجاد کننده حرکت یا نیرو، موضوع شاخه‌ای از فیزیک مکانیک به نام «حرکت‌شناسی یا سینماتیک» (Kinematics) است. در سینماتیک با توجه به تغییرات سرعت جسم، می‌توانیم نوع حرکت آن را در یکی از دو گروه زیر قرار دهیم:

• حرکت با سرعت ثابت (حرکت یکنواخت)
• حرکت با سرعت متغیر (حرکت شتابدار)

دقت کنید منظور ما از ثابت یا متغیر بودن سرعت، تغییرات آن در طول زمان است. اگر پس از گذشت مدت زمان مشخصی سرعت جسم عوض نشود، می‌گوییم حرکت جسم با سرعت ثابت انجام شده است. این در حالی است که اگر مقدار سرعت جسم با گذشت زمان کمتر یا بیشتر شود یا حتی بدون تغییر اندازه، فقط جهت سرعت جسم تغییر کند، در هر دو حالت شتاب خواهیم داشت.

در حرکت شتابدار نیز ممکن است شتاب ایجاد شده ثابت یا متغیر باشد. برای مثال، معمولا هر جسمی که به سمت زمین می‌افتد (سقوط آزاد)، دارای شتاب ثابتی است و حرکت آن از نوع حرکت با شتاب ثابت محسوب می‌شود. در این مطلب تمرکز ما روی حرکت با سرعت ثابت است. به‌ویژه قصد داریم پس از معرفی فرمول سرعت ثابت، چگونگی استفاده از این فرمول‌ را در حل مسائل این حوزه با هم بررسی کنیم.

هر کدام از ما احتمالا حرکت با سرعت ثابت را تجربه کرده‌ایم. برای مثال، زمانی که در حال رانندگی در جاده با سرعت ثابتی هستید یا زمانی که در یک هواپیمای در حال حرکت با سرعت ثابت در یک مسیر مستقیم، نشسته‌اید. البته در واقعیت، در این مثال‌ها حرکت در بازه‌های زمانی محدودی از نوع سرعت ثابت محسوب می‌شود، چون همواره عوامل خارجی مانند سرعت باد یا افت و خیزهای سطح جاده روی سرعت تاثیر دارند و عملا حرکت از سرعت ثابت خارج می‌شود.

تندی و سرعت چه تفاوتی با هم دارند؟

می‌دانیم که «سرعت» (Velocity) یک کمیت برداری است، یعنی علاوه بر اندازه، جهت آن نیز مهم است. بنابراین اولین سوالی که مطرح می‌شود این است که ثابت بودن یک کمیت برداری مانند سرعت به چه معنا است؟ برای پاسخ دادن به این سوال از دانش خود راجع‌به انوع کمیت‌‌ها در فیزیک استفاده می‌کنیم.

برای مثال، شرایطی را در نظر بگیرید که دمای اتاق $$30 \ C$$ است. پس از گذشت مدت زمان مشخصی، متوجه می‌شوید که دمای اتاق همچنان $$30 \ C$$ است. در این حالت می‌توانید بگویید دما ثابت مانده است. در این مثال، دما یک کمیت عددی، نرده‌ای یا اسکالر است و ثابت ماندن آن در طول زمان، مستلزم در نظر گرفتن تغییرات مقدار یا اندازه آن است.

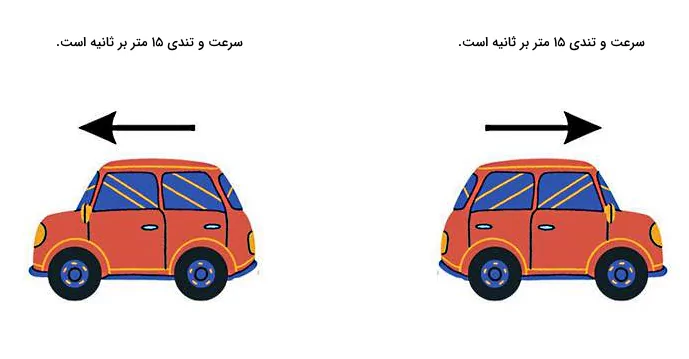
اما در مورد کمیت‌‌های برداری وضعیت متفاوت است. می‌دانیم دو بردار زمانی با هم برابر هستند که اندازه و جهت هر دو کاملا مشابه هم باشد. بنابراین ثابت ماندن سرعت به این معنا است که نه‌تنها اندازه آن، بلکه جهت آن هم تغییری نکند. برای مثال اگر اندازه سرعت ثابت بماند، اما جهت آن عوض شود، در شرایط حرکت با سرعت ثابت نیستیم. در سینماتیک به علت اهمیت تمایز اندازه و جهت سرعت، اندازه سرعت را «تندی» (Speed) می‌نامند.

حرکت ذره‌ای در راستای مثبت محور xها و با سرعتی به اندازه $$5 \ \frac{m}{s}$$ را در لحظه $$t_1$$ نظر بگیرید. اگر پس از گذشت مدت زمان مشخصی در لحظه‌ای برابر با $$t_2$$، همچنان ذره در حال حرکت با همین مقدار سرعت و در همین جهت باشد، حرکت آن از نوع سرعت ثابت محسوب می‌شود. برای اینکه بتوانیم جهت کمیت‌های برداری مانند سرعت را واضح‌تر نشان دهیم، مرسوم است که از بردارهایی با اندازه واحد، به نام بردار یکه استفاده کنیم. این بردارها به‌صورت زیر تعریف می‌شوند:

اندازه هر کدام از این بردارها برابر است با یک. در نتیجه اگر هر کدام از این بردارها را در کنار یک عدد قرار دهیم، تغییری در اندازه آن عدد ایجاد نمی‌شود و تنها کارکرد این بردارها، نشان دادن جهت آن عدد است. پس ثابت بودن سرعت در مثال بالا را می‌توانیم به شکل زیر نمایش دهیم:

$$\vec{v}=\begin{cases}5\hat{i} & t=t_1\\5\hat{i} & t=t_2\end{cases}$$

حالا موقعیتی را تصور کنید که ذره در لحظه $$t_2$$ شروع می‌کند به حرکت در راستای مثبت محور y با سرعتی به اندازه $$5 \ \frac{m}{s}$$. در این شرایط، حرکت ذره در بازه زمانی $$\triangle t=t_2-t_1$$ دیگر یک حرکت با سرعت ثابت محسوب نمی‌شود، چون داریم:

$$\vec{v}=\begin{cases}5\hat{i} & t=t_1\\5\hat{j} & t=t_2\end{cases}$$

در حقیقت در موقعیت دوم تندی ذره ثابت است، اما سرعت آن نه. تندی معادل است با اندازه سرعت، که در هر دو موقعیت برابر است با عدد $$5 \ \frac{m}{s}$$. بنابراین با ثابت ماندن تندی جسم در یک بازه زمانی مشخص، در صورتی حرکت آن سرعت ثابت محسوب می‌شود که جهت حرکت آن نیز تغییر نکند. عموما جهت سرعت در راستای جهت حرکت جسم است، بنابراین اگر بخواهیم سرعت جسم ثابت بماند، علاوه بر اینکه اندازه سرعت نباید تغییر کند، لازم است جهت حرکت جسم نیز عوض نشود. بر این اساس، حرکت جسم در یک مسیر مستقیم معمولا حرکت با سرعت ثابت محسوب می‌شود.

مثال حرکت دایره‌ای

ذره‌ای را در نظر بگیرید که مطابق شکل زیر در یک مسیر دایره‌ای با تندی ثابت برابر با $$v$$ در حال حرکت است. می‌خواهیم بررسی کنیم که آیا در این حرکت سرعت ذره ثابت می‌ماند یا خیر. همان‌طور که مشاهده می‌کنید، بردارهای سرعت در سه نقطه روی این مسیر شامل نقاط $$A$$ و $$B$$ و$$C$$ رسم شده‌اند. پس برای تشخیص سرعت یا برای رسم بردار سرعت، کافی است جهت حرکت جسم در مسیر را در نظر بگیریم. در یک مسیر دایره‌ای، همیشه بردار سرعت بر مسیر مماس است.

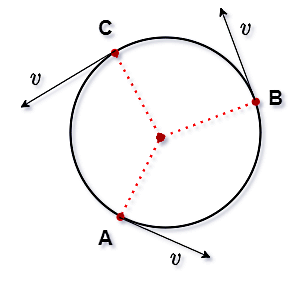
در سه نقطه انتخابی، اگر چه تندی یا اندازه سرعت یکسان و برابر با $$v$$ است، اما جهت‌ این سرعت‌ها متفاوت است. به حرکت جسم در یک مسیر دایره‌ای، حرکت دایره‌ای گفته می‌شود. پس نتیجه اینکه حرکت دایره‌ای جسمی با تندی ثابت، حرکت با سرعت ثابت محسوب نمی‌شود.

حرکت یکنواخت

همان‌طور که اشاره شد، به حرکت با سرعت ثابت حرکت یکنواخت هم گفته می‌شود. برخی از خصوصیات حرکت یکنواخت که از ثابت ماندن سرعت ناشی می‌شوند، عبارت‌اند از:

• تندی و جهت سرعت، هیچ‌کدام در طول حرکت تغییر نمی‌کنند.
• شتاب جسم برابر است با صفر.
• مسافت طی شده توسط جسم در هر ثانیه یکسان است.
• معادله‌ حرکت جسم به‌صورت $$x=vt+x_0$$ است.

حرکت ماشین‌ها در بزرگراه با تندی ثابت یا حرکت قطار روی ریل، مثال‌هایی از حرکت یکنواخت هستند.

قانون اول نیوتن و حرکت با سرعت ثابت

برای اینکه درک بهتری نسبت به علت ثابت ماندن سرعت داشته باشیم، در این بخش به مفهوم و نتایج قانون اول نیوتن رجوع می‌کنیم. مفهوم سرعت ثابت کاملا به اثر نیرو و قانون اول نیوتن مرتبط است. طبق قانون اول نیوتن، موقعیت فیزیکی یک جسم همواره در یکی از دو حالت زیر قرار دارد:

• یا جسم در حال حرکت است.
• یا جسم ساکن است.

همچنین در قانون اول می‌خواهیم ببینیم وضعیت حرکت جسم در شرایطی که مجموع نیروهای وارد بر آن صفر است، چگونه است. با توجه به دو موقعیت بالا، نتیجه اعمال این قانون به شکل زیر خواهد شد:

• جسم در حال حرکت: جسم به حرکت خود با سرعت ثابت ادامه می‌دهد.
• جسم ساکن: جسم ساکن می‌ماند.

اولین نتیجه‌گیری به موضوع ما ربط دارد و طبق آن، اگر هیچ نیرویی به جسم در حال حرکت وارد نشود، جسم با سرعت ثابت به حرکت خود ادامه می‌دهد. این حرکت با سرعت ثابت مادامی که مجموع نیروهای واد بر جسم صفر بماند، ادامه دارد. اما در واقعیت، امکان ندارد چنین حرکتی تا ابد داشته باشیم. طبق قانون اول، حرکت با سرعت ثابت مستلزم این است که هیچ نیرویی به جسم وارد نشود یا اگر چند نیرو به جسم وارد می‌شوند، جمع برداری این نیروها صفر شود.

احتمال رخ دادن چنین شرایطی بسیار ضعیف است، چون همواره نیروهایی مانند اصطکاک یا مقاومت هوا به یک جسم در حال حرکت وارد می‌شوند. این توضیحات در قالب ریاضیات به وسیله قانون دوم نیوتن نشان داده می‌شوند که در بخش‌های قبل نیز به آن اشاره شد:

$$\vec{v}=constant \Rightarrow \sum \vec{F}=0$$

نمودارهای حرکت با سرعت ثابت

پس از اینکه آموختیم حرکت با سرعت ثابت چه مفهومی دارد و انواع فرمول سرعت ثابت چیست، در این بخش می‌خواهیم به توضیح نمودارهایی که این نوع حرکت را توصیف می‌کنند، بپردازیم. نمودارهای این حرکت به سه گروه تقسیم می‌شوند:

• نمودار مکان - زمان
• نمودار سرعت - زمان
• نمودار شتاب - زمان

در ادامه هر کدام را توضیح می‌دهیم.

نمودار مکان - زمان

اگر خاطرتان باشد، در ابتدای این نوشته راجع‌به معادله مکان - زمان جسم در حرکت با سرعت ثابت صحبت کردیم و گفتیم که این معادله در حقیقت همان فرمول سرعت ثابت محسوب می‌شود. همچنین توضیح دادیم که نمودار مکان - زمان جسم در حرکت با سرعت ثابت به شکل یک خط راست است. این خط همیشه محور عمودی یا محور مکان را در یک نقطه قطع می‌کند، مگر اینکه جسم متوقف شود. بنابراین همان‌طور که در شکل زیر مشاهده می‌کنید، اگر چه جابجایی جسم نسبت به زمان زیاد می‌شود، اما سرعت جسم همیشه ثابت است:

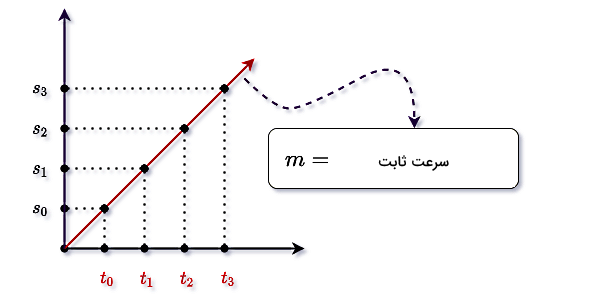
نمودار سرعت - زمان

یکی دیگر از نمودارهای مهم حرکت با سرعت ثابت، نمودار سرعت - زمان است. در این نمودار سرعت روی محور عمودی قرار می‌گیرد و تغییرات آن با زمان در قالب نمودار نمایش داده می‌شود. چون در حرکت با سرعت ثابت، سرعت عوض نمی‌شود، بنابراین رسم این نمودار با اتصال نقاطی انجام می‌شود که شامل زمان‌های مختلف اما سرعت‌هایی برابر هستند:

1. $$(0, v)$$
2. $$(t_0, v)$$
3. $$(t_1, v)$$
4. $$(t_2, v)$$
5. $$(t_3, v)$$

پس در حرکت سرعت ثابت، با گذشت زمان همواره مقدار سرعت عدد ثابتی می‌ماند و نمودار سرعت - زمانی به شکل زیر خواهیم داشت که همیشه به شکل یک خط راست و موازی با محور زمان است:

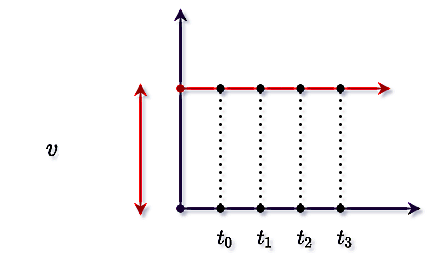
یکی از مهم‌ترین کاربردهای نمودار سرعت - زمان در حرکت با سرعت ثابت این است که با در اختیار داشتن این نمودار، می‌توانیم جابجایی کل جسم را با محاسبه مساحت زیر این نمودار تعیین کنیم. برای مثال در نمودار سرعت - زمان زیر می‌توانیم جابجایی جسم را با محاسبه مساحت بین نمودار سرعت - زمان و محور افقی پیدا کنیم. این مساحت در شکل زیر معادل است با مساحت مستطیلی با ابعاد $$t_1-t_0$$ و $$v$$. پس اگر جابجایی را با $$d$$ نشان دهیم، مقدار آن از رابطه زیر به‌دست می‌آید:

$$d=v(t_1-t_0)$$

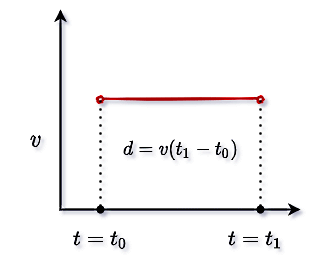
نمودار شتاب - زمان

در بخش‌‌های گذشته توضیح دادیم که در حرکت با سرعت ثابت، چون اندازه و جهت سرعت تغییر نمی‌کند، شتاب لحظه‌ای و شتاب متوسط نداریم. پس اگر بخواهیم نمودار شتاب بر حسب زمان را برای این نوع حرکت رسم کنیم، شکل زیر حاصل خواهد شد:

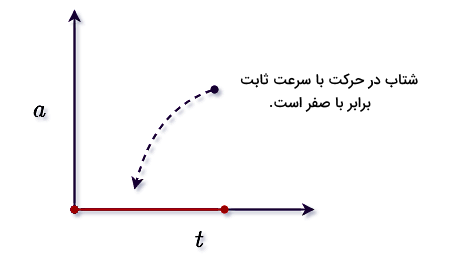
در تصویر بالا، صفر ماندن شتاب با گذر زمان به‌ شکل خط قرمز رنگی روی محور زمان نشان داده شده است. در ادامه این مطلب، با بررسی مثال‌‌های مختلف متوجه خواهید شد که چگونه می‌توانیم از فرمول سرعت ثابت در کنار اطلاعات حاصل این نمودارها برای حل مسائل مختلف استفاده کنیم.

حل مثال و تمرین از فرمول سرعت ثابت

توضیحات بخش‌های قبل، جهت استفاده از فرمول سرعت ثابت در حل مسائل مختلف سینماتیک و حرکت با سرعت ثابت بیان شد. در این بخش می‌خواهیم آموخته‌های خود از بخش‌های قبل را با حل چند مثال و تمرین بیازماییم.

مثال ۱

راننده اتومبیلی در حال رانندگی در مسیر جاده مستقیمی از شهری به شهر دیگر با سرعت ثابت $$78 \ \frac{km}{h}$$ است. اگر کل سفر این شخص $$44 \ min$$ طول بکشد، چه مسافتی طی کرده است؟

پاسخ

برای اینکه بتوانیم از فرمول سرعت ثابت $$x=vt+x_0$$ در حل این سوال استفاده کنیم، باید ابتدا مقادیر $$x_0$$ و $$t_0$$ را مشخص کنیم. مرسوم است نقطه شروع را صفر در نظر بگیریم، مگر اینکه در صورت سوال راجع‌به مشخصات شروع حرکت صحبت شده باشد. بنابراین با در نظر گرفتن $$x_0=0$$ و $$t_0=0$$ خواهیم داشت:

$$x_0=0 \Rightarrow x=vt$$

دقت کنید در معادله مکان - زمان، $$t$$ در حقیقت همان بازه زمانی $$t-t_0$$ است که چون غالبا $$t_0=0$$، به‌ صورت $$t$$ نوشته می‌شود. حالا با توجه به مشخص بودن سرعت و زمان و اینکه می‌دانیم در تمام مسیر مقدار و جهت سرعت ثابت می‌ماند، کافی است اعداد داده شده را در فرمول بالا جای‌گذاری کنیم. اما پیش از آن باید به واحدها دقت شود. اگر زمان را بر حسب ساعت بنویسیم، مسافت طی شده بر حسب کیلومتر به‌دست می‌آید. می‌دانیم یک ساعت شصت دقیقه است:

$$44 \ min = 44 \ min \times \frac{1 \ hour}{60 \ min}=0.73 \ h$$

$$\Rightarrow x=vt = 78 \ \frac{km}{h} \times0.73 \ h =57 \ km$$

مثال ۲

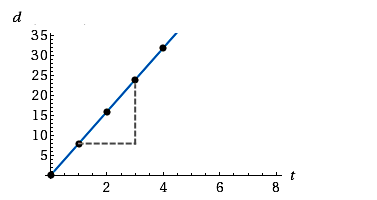
نمودار مکان (متر) بر حسب زمان (ثانیه) جسمی به‌صورت زیر است. سرعت متوسط این جسم در بازه زمانی نشان داده شده روی شکل چقدر است؟ آیا حرکت این جسم، یک حرکت سرعت ثابت محسوب می‌شود؟

پاسخ

همان‌طور که گفتیم، محاسبه سرعت متوسط با فرمول زیر امکان‌پذیر است:

$$v=\frac{\triangle x}{\triangle t}=\frac{x_2-x_1}{t_2-t_1}$$

طبق شکل بالا، باید خط‌چین افقی را به‌عنوان بازه زمانی و خط‌چین عمودی را به عنوان بازه مکانی یا مکان‌های متناظر با بازه زمانی موردنظر، در فرمول بالا قرار دهیم. به این ترتیب، جسم در زمان $$t_1=1 \ s$$ در مکان تقریبی $$x_1=8 \ m$$ و در زمان $$t_2=3 \ s$$ در مکان تقریبی $$x_2=24 \ m$$ قرار دارد. پس سرعت متوسط جسم در این بازه برابر خواهد شد با:

$$\Rightarrow v=\frac{x_2-x_1}{t_2-t_1}=\frac{24-8}{3-1}=\frac{16}{2}=8 \ \frac{m}{s}$$

در پاسخ به سوال دوم، با توجه به اینکه نمودار مکان - زمان یک خط مستقیم با شیب ثابتی است، می‌توانیم بگوییم بله، حرکت سرعت ثابت محسوب می‌شود و این سرعت برابر است با $$8 \ \frac{m}{s}$$.

مثال ۳

فرض کنید اتومبیلی در حال حرکت در جاده صافی با سرعت ثابت $$90 \ \frac{km}{h}$$ است. اگر بدانیم در یک نقطه مشخص، کامیونی که با سرعت ثابت $$70 \ \frac{km}{h}$$ حرکت می‌کند، $$10 \ km$$ از اتومبیل جلوتر است، چقدر طول می‌کشد تا اتومبیل به کامیون برسد و در این لحظه، هر کدام در چه مکانی قرار دارند؟

پاسخ

برای اینکه بتوانیم پاسخ روشنی به این سوال بدهیم، فرض کنید مسیر حرکت اتومبیل و کامیون در این جاده به شکل زیر در راستای مثبت محور xها است. حالا اگر بخواهیم موقعیت کامیون و اتومبیل را روی این مسیر نشان دهیم، باید کامیون را $$10 \ km$$ جلوتر از اتومبیل قرار دهیم. پس مکان اولیه اتومبیل و کامیون در لحظه شروع یا $$t_0$$ که برابر با صفر در نظر گرفته می‌شود، به‌ترتیب برابر هستند با $$x_{C,0}=0$$ و $$x_{T,0}=10 \ km$$.

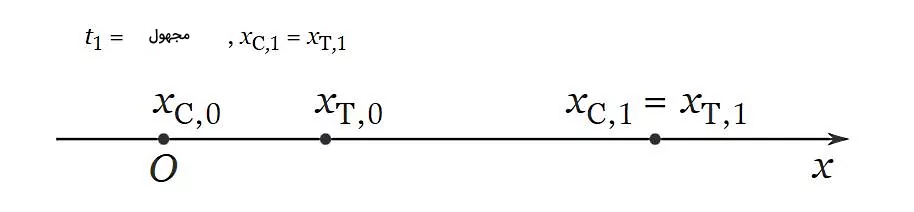
سپس در زمان جلوتری مانند $$t_1$$ که مجهول مسئله است، اتومبیل به کامیون می‌رسد. در این لحظه مکان اتومبیل و کامیون باید یکی شود، یعنی داریم:

$$x_{C,1}=x_{T,1}$$

حالا که وضعیت حرکتی دو جسم متحرک را مشخص کردیم، فرمول سرعت ثابت یا همان معادله مکان - زمان را برای هر کدام جدا می‌نویسیم. ابتدا برای اتومبیل داریم:

$$x=vt+x_0$$

$$\Rightarrow x_{C}=v_C(t-t_0)+x_{C,0}$$

با توجه به صفر بودن مکان و زمان اولیه اتومبیل، فرمول بالا به‌صورت زیر می‌شود:

$$\Rightarrow x_{C}=v_Ct$$

حالا همین معادله را برای کامیون می‌نویسیم:

$$\Rightarrow x_{T}=v_T(t-t_0)+x_{T,0}$$

$$\Rightarrow x_{T}=v_Tt+10$$

گفتیم که در لحظه نامعلومی به نام $$t_1$$، مکان نهایی دو وسیله برابر می‌شود. پس با جای‌گذاری $$t_1$$ به‌جای $$t$$ در دو معادله حرکت به‌دست آمده و برابر قرار دادن مکان‌های نهایی $$x_{C,1}$$ و $$x_{T,1}$$ خواهیم داشت:

$$\Rightarrow v_Ct_1=v_Tt_1+10$$

$$\Rightarrow t_1(v_C-v_T)=10$$

$$\Rightarrow t_1=\frac{10}{90-70}=0.5 \ h$$

دقت کنید چون سرعت‌ها بر حسب کیلومتر بر ساعت داده شده‌اند، زمان موردنظر نیز بر حسب ساعت به‌دست آمد. بنابراین اتومبیل با همین مقدار سرعت ثابت خود، پس از نیم ساعت به کامیون می‌رسد. در بخش دوم سوال، پرسیده شده است که در این لحظه مکان نهایی هر کدام از دو وسیله کجاست. پس از گذشت نیم ساعت، مکان نهایی هر دو وسیله مشابه هم است. پس کافی است این بازه زمانی را در یکی از دو معادله حرکت قرار دهیم و مکان نهایی را محاسبه کنیم. برای مثال با قرار دادن $$t_1=0.5 \ h$$ در معادله زیر خواهیم داشت:

$$\Rightarrow x_{C}=v_Ct_1=90\times 0.5=45 \ km$$

مثال ۴

سرعت جسمی که یک مسیر دایره‌ای با شعاع $$3 \ m$$ را طی مدت زمان $$4 \ s$$ می‌پیماید، چقدر است؟ آیا این حرکت سرعت ثابت است؟

پاسخ

همان‌طور که در بخش حرکت دایره‌ای توضیح دادیم، پیمایش مسیر دایره‌ای یک حرکت با سرعت ثابت محسوب نمی‌شود، چون جهت سرعت در حال عوض شدن است. ولی تندی این حرکت که همان اندازه سرعت است، ثابت است. با در نظر گرفتن مکان و زمان اولیه برابر با صفر، خواهیم داشت:

$$ x=vt+x_0 $\Rightarrow x=vt$$

$$\Rightarrow v= \frac{x}{t}$$

اما در این سوال مسیر دایره‌ای پیموده شده توسط جسم را نداریم که با قرار دادن شعاع در فرمول محیط دایره، به شکل زیر محاسبه می‌شود:

$$x=2\pi r \Rightarrow v= \frac{(2)(3.14)(3)}{4}=4.71 \ \frac{m}{s}$$

مثال ۵

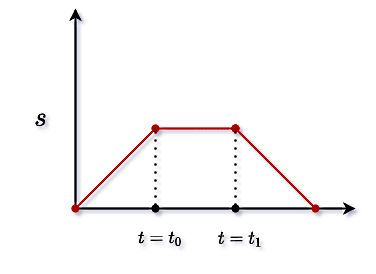
فرض کنید نمودار مکان - زمان حرکت جسمی به‌صورت زیر است. معادله مکان - زمان این حرکت بنویسید و سپس نمودار سرعت - زمان را رسم کنید:

پاسخ

دقت کنید در این سوال مقادیر عددی نداریم، اما می‌توانیم با در نظر گرفتن پارامترها، نمودار سرعت - زمان را به کمک فرمول‌ سرعت ثابت رسم کنیم. می‌دانیم معادله مکان - زمان به شکل زیر است:

$$x=vt+x_0$$

اما زمانی مجاز به نوشتن این رابطه هستیم که حرکت ما از نوع سرعت ثابت باشد. نمودار حرکت این جسم متشکل از سه خط راست مختلف است، بنابراین می‌توانیم حرکت آن را در کل سرعت ثابت در نظر بگیریم. چون سه خط راست با شیب‌های مختلف داریم، پس احتمالا حرکت کامل این جسم شامل سه حرکت با سرعت‌های ثابت متفاوت بوده است. ابتدا لازم است حرکت جسم را بر اساس نمودار مکان - زمان تحلیل کنیم.

با در نظر گرفتن مبدا حرکت به‌صورت $$(0, 0)$$، با گذشت زمان مکان جسم هم زیاد می‌شود تا اینکه به لحظه $$t_0$$ می‌رسیم. از این لحظه تا لحظه $$t_1$$، مکان جسم تغییری نمی‌کند. پس از لحظه $$t_1$$، مکان جسم با گذشت زمان کاهش می‌یابد تا اینکه در لحظه آخر که ما آن را $$t_2$$ می‌نامیم و در شکل نشان داده نشده است، مکان جسم مجددا برابر با صفر می‌شود.

پس حرکت این جسم را در سه بازه زمانی مختلف به شکل زیر بررسی کردیم:

1. $${\triangle t}_1=t_0-0$$
2. $${\triangle t}_2=t_1-t_0$$
3. $${\triangle t}_3=t_2-t_1$$

حالا با در نظر گرفتن مکانی با اندازه $$s$$ در لحظات $$t_0$$ و $$t_1$$، می‌توانیم فرمول سرعت متوسط یعنی $$v=\frac{\triangle s}{\triangle t}$$ را برای هر کدام از این بازه‌ها بنویسیم:

1. $$v_1=\frac{s-0}{t_0-0}=\frac{s}{t_0}$$
2. $$v_2=\frac{s-s}{t_1-t_0}=0$$
3. $$v_3=\frac{0-s}{t_2-t_1}=\frac{-s}{t_2-t_1}$$

در اولین بازه زمانی، حرکت جسم با سرعت ثابتی به اندازه $$v_1$$ انجام می‌شود. پس معادله مکان - زمان برای این بازه به‌صورت زیر خواهد شد:

$$x=vt+x_0 \Rightarrow x=v_1t$$

چون در لحظه شروع مکان اولیه برابر با صفر است، پس $$x_0=0$$. معادله بالا، همان معادله اولین خط در تصویر و در بازه $${\triangle t}_1=t_0-0$$ است که شیب مثبتی دارد. در بازه زمانی بعدی، باز هم به نوعی حرکت با سرعت ثابت داریم، اما مقدار عددی این سرعت صفر است ($$v_2=0$$). پس معادله مکان - زمان در این بازه می‌شود:

$$x=vt+x_0 \Rightarrow x=0+x_0$$

تفاوت این بازه زمانی با بازه زمانی قبلی این است که در این بخش از حرکت، مکان اولیه برابر است با $$s$$. پس معادله خط در بازه زمانی $${\triangle t}_2=t_1-t_0$$ برابر خواهد شد با:

$$\Rightarrow x=s$$

همان‌طور که در تصویر صورت سوال مشاهده می‌کنید، در دومین بازه زمانی یک خط افقی و موازی با محور زمان داریم که شیب آن صفر است. در واقع بدون محاسبه و استفاده از فرمول سرعت ثابت از روی شیب صفر این بخش از حرکت، می‌توانستیم حدس بزنیم که در این بخش سرعت جسم صفر است. پس معادله مکان - زمان با در نظر گرفتن $$v=0$$ به شکل بالا خواهد شد.

در نهایت سومین بازه زمانی سرعتی با اندازه $$v_3$$ به ما داد. پس معادله مکان - زمان برای این بازه به‌صورت زیر محاسبه می‌شود:

$$x=vt+x_0 \Rightarrow x=v_3t+s$$

در لحظه شروع این بازه یعنی در $$t_1$$، مکان جسم معادل $$s$$ است، پس $$x_0=s$$. این معادله سومین خط در تصویر است که شیب منفی دارد و اگر به مقدار محاسبه شده برای $$v_3$$ توجه کنید، خواهید دید که در محاسبات هم سرعت ثابت این بازه زمانی منفی شد.

دقت کنید در سه معادله به‌دست آمده، $$x$$ و $$t$$ به‌عنوان متغیرهای معادله مکان - زمان در نظر گرفته شده‌اند که می‌توانند اعدا مختلفی بپذیرند. اما مقادیر $$s$$ و $$t_0$$ و $$t_1$$ و $$t_2$$ در این سوال ثابت است. پس معادلات مکان - زمان این حرکت به شکل زیر تعیین شد:

$$\begin{cases}x=v_1t & {\triangle t}_1=t_0-0\\ x=s &{\triangle t}_2=t_1-t_0\\ x=v_3t+s & {\triangle t}_3=t_2-t_1\end{cases}$$

برای رسم نمودار سرعت - زمان کافی است در صفحه مختصات، محور عمودی را سرعت و محور افقی را زمان در نظر بگیریم. سپس در هر کدام از سه بازه زمانی تعیین شده، سرعت را به شکل خط راستی موازی با محور افق رسم می‌کنیم:

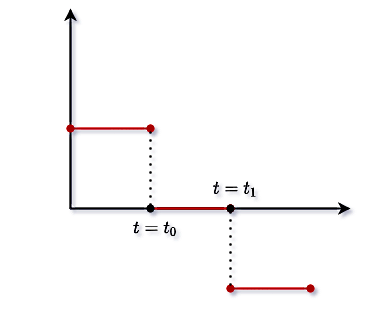
طبق محاسبات، سرعت در اولین بازه زمانی دارای مقداری ثابت و مثبت، در دومین بازه صفر و در سومین بازه دارای مقداری ثابت و منفی بود.

مثال ۶

بین خانه مریم و خانه خانواده‌اش تقریبا $$115 \ mile$$ فاصله وجود دارد. آ‌ن‌ها تصمیم گرفته‌اند در رستورانی که در مسیر بین خانه‌هایشان قرار دارد، یکدیگر را ببینند. می‌دانیم مریم با تندی متوسط $$10 \ \frac{mile}{h}$$ سریع‌تر از خانواده‌اش رانندگی می‌کند. چنانچه مدت زمان رانندگی مریم و خانواده‌اش به ترتیب برابر با $$1.5 \ h$$ و $$1 \ h$$ باشد، تندی متوسط حرکت مریم و خانواده‌اش چقدر است؟

پاسخ

برای اینکه دید بهتری نسبت به سوال داشته باشیم، بهتر است نمودار حرکت مریم و خانواده‌اش را به شکل زیر رسم کنیم:

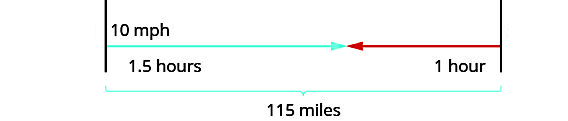
با توجه به اینکه هر دو حرکت در یک مسیر مستقیم است، بنابراین هر دو حرکت سرعت ثابت محسوب می‌شوند. پس می‌توانیم فرمول سرعت ثابت را به شکل معادله مکان - زمان برای حرکت مریم ($$m$$) و خانواده‌اش ($$f$$) به‌صورت زیر بنویسیم:

$$x=vt+x_0$$

$$x=v_mt_m$$

$$x=v_ft_f$$

در معادلات بالا نقطه شروع حرکت را برای مریم و خانواده‌اش صفر در نظر گرفته‌ایم و مکان نهایی هر دو نیز با هم برابر است:

$$\Rightarrow v_ft_f=v_mt_m$$

از طرفی طبق صورت سوال می‌توانیم بنویسیم: $$v_m=v_f+10$$.

$$\Rightarrow v_ft_f=(v_f+10)t_m$$

حالا عددگذاری می‌کنیم:

$$\Rightarrow 1v_f=1.5(v_f+10)=1.5v_f+15$$

$$\Rightarrow -0.5v_f=15 \Rightarrow v_f=-30 \ \frac{mile}{h}$$

$$\Rightarrow v_m=v_f+10=30+10=40\ \frac{mile}{h}$$

با توجه به اینکه حرکت خانواده در خلاف جهت مثبت محور xها بوده است، سرعت این حرکت منفی شده است. اما باید دقت داشته باشید که در محاسبه سرعت حرکت مریم، نیازی نیست علامت منفی درج شود.

مثال ۷

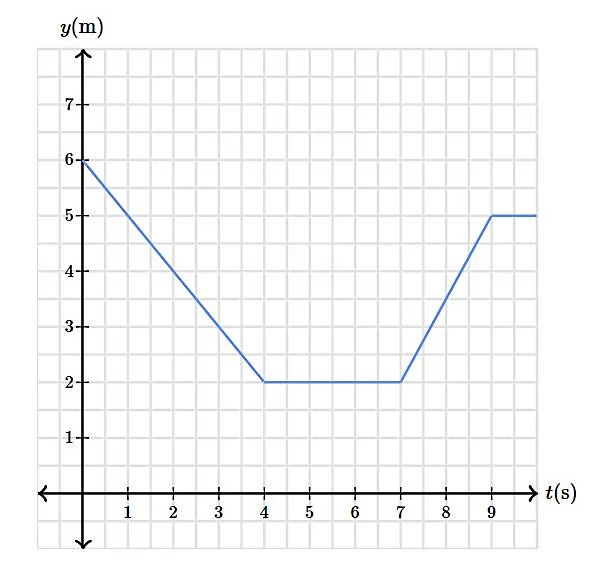
اگر نمودار مکان - زمان حشره‌ای به‌ صورت زیر باشد، آیا حرکت این حشره یک حرکت با سرعت ثابت محسوب می‌شود؟ سرعت ثابت و معادله مکان - زمان این حرکت را تعیین کنید:

پاسخ

اگر به نمودار بالا دقت کنید، چون در کل زمان نشان داده شده نمودار مکان بر حسب زمان به شکل خطوط راست است، بنابراین حرکت در بازه‌های زمانی مختلف سرعت ثابت محسوب می‌شود. اما مقدار سرعت در بازه‌های مختلف متفاوت است و همین مسئله باعث شده است تا خطوط ما به شکل‌های مختلفی باشند. می‌توانیم چهار بازه زمانی به‌صورت زیر در نظر بگیریم و مقدار سرعت را برای هر بازه تعیین کنیم:

1. $${\triangle t}_1=4-0=4 \ s$$
2. $${\triangle t}_2=7-4=3 \ s$$
3. $${\triangle t}_3=9-7=2 \ s$$
4. $${\triangle t}_3=10-9=1 \ s$$

اگر مبدا حرکت را در نقطه $$(0, 0)$$ در نظر بگیریم، با گذشت مدت زمان $$4 \ s$$، مکان حشره از $$6 \ m$$ کاهش می‌یابد و به $$2 \ m$$ می‌رسد. از لحظه $$4 \ s$$ تا لحظه $$7 \ s$$، مکان حشره تغییری نکرده است. پس از لحظه $$7 \ s$$، مکان با گذشت زمان افزایش می‌یابد تا اینکه در لحظه $$9 \ s$$ مجددا حشره متوقف می‌شود.

پس می‌توانیم با در نظر گرفتن مکان‌های متناظر، فرمول سرعت متوسط یعنی $$v=\frac{\triangle s}{\triangle t}$$ را برای هر کدام از این بازه‌ها بنویسیم و آن را محاسبه کنیم:

1. $$v_1=\frac{2-6}{4-0}=\frac{-4}{4}=-1 \ \frac{m}{s}$$
2. $$v_2=\frac{2-2}{7-4}=\frac{0}{3}=0 \ \frac{m}{s}$$
3. $$v_3=\frac{5-2}{9-7}=\frac{3}{2}=1.5 \ \frac{m}{s}$$
4. $$v_4=\frac{5-5}{10-9}=\frac{0}{1}=0 \ \frac{m}{s}$$

در اولین بازه زمانی، حرکت جسم با سرعت ثابتی به اندازه $$-1 \ \frac{m}{s}$$ انجام می‌شود. پس معادله مکان - زمان برای این بازه به‌صورت زیر خواهد شد:

$$x=vt+x_0 \Rightarrow x=v_1t=-t$$

چون در لحظه شروع مکان اولیه برابر با صفر است، پس $$x_0=0$$. این معادله توصیف کننده خط راستی با شیب منفی است، همان‌طور که از نمودار مشخص بود. در بازه زمانی بعدی، باز هم به نوعی حرکت با سرعت ثابت داریم، اما مقدار عددی این سرعت صفر است ($$v_2=0$$). پس معادله مکان - زمان در این بازه می‌شود:

$$x=vt+x_0 \Rightarrow x=0+x_0$$

تفاوت این بازه زمانی با بازه زمانی قبلی این است که در این بخش از حرکت، مکان اولیه برابر است با $$x_0 =2 \ m$$. پس معادله خط در بازه زمانی $${\triangle t}_2=7-4=3 \ s$$ برابر خواهد شد با:

$$\Rightarrow x=2$$

در سومین بازه زمانی سرعت برابر شد با $$v_3=1.5 \ \frac{m}{s}$$. پس معادله مکان - زمان برای این بازه به‌صورت زیر محاسبه می‌شود:

$$x=vt+x_0 \Rightarrow x=1.5t+2$$

در لحظه شروع این بازه، مکان جسم معادل است با $$x_0=2$$. این معادله سومین خط در تصویر است که شیب مثبتی دارد. برای چهارمین و آخرین بازه زمانی با در نظر گرفتن $$x_0=5$$ و سرعت صفر خواهیم داشت:

$$x=vt+x_0 \Rightarrow x=5$$

بنابراین مقادیر سرعت ثابت و معادلات مکان - زمان این حرکت به شکل زیر تعیین شدند:

$$\begin{cases}v_1=-1 & {\triangle t}_1\\ v_2=0 &{\triangle t}_2\\ v_3=1.5 & {\triangle t}_3\\ v_4=0 & {\triangle t}_4\end{cases}$$

$$\begin{cases}x=-t & {\triangle t}_1\\ x=2 &{\triangle t}_2\\ x=1.5t+2 & {\triangle t}_3\\ x=5 & {\triangle t}_4\end{cases}$$

مثال ۸

با توجه به نمودار زیر، معادله مکان - زمان را بنویسید:

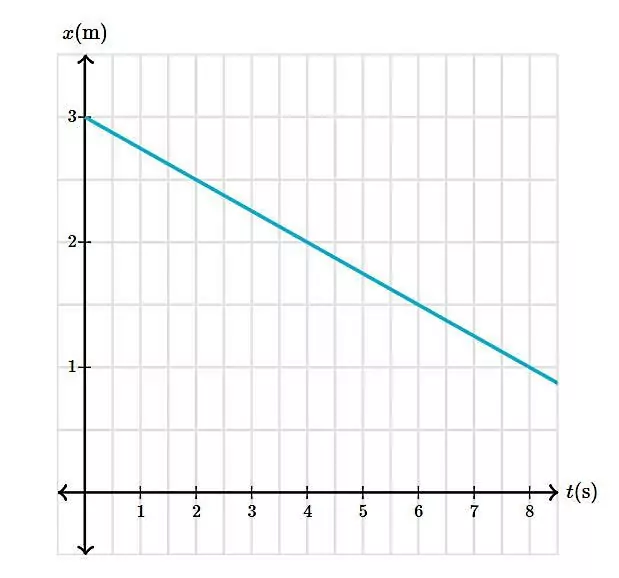
پاسخ

با توجه به نمودار مکان - زمانی که در اختیار داریم، ابتدا باید سرعت ثابت را پیدا کنیم و سپس به کمک فرمول سرعت ثابت، معادله مکان - زمان را بنویسیم. برای یافتن سرعت ثابت، کافی است بازه زمانی مشخصی برای مثال از $$t_0=4 \ s$$ تا $$t=8 \ s$$ را در نظر بگیریم. سپس مکان‌های متناظر با این دو لحظه را روی نمودار پیدا کنیم و با فرمول زیر، سرعت را محاسبه کنیم:

$$v=\frac{\triangle x}{\triangle t}=\frac{x-x_0}{t-t_0}$$

$$\Rightarrow v=\frac{1-2}{8-4}=-0.25 \ \frac{m}{s}$$

دقت کنید چون نمودار ما به شکل یک خط راست است، بنابراین شیب این خط در تمام لحظات یکسان است. پس فرقی ندارد چه بازه زمانی برای محاسبه سرعت انتخاب شود. بنابراین سرعت ثابت برای تمام لحظات نشان داده شده در نمودار بالا برابر شد با $$-0.25 \ \frac{m}{s}$$. حالا می‌توانیم معادله مکان - زمان این حرکت را با فرمول زیر بنویسیم:

$$x=vt+x_0$$

$$\Rightarrow x=-0.25t+3$$

دقت کنید برای تعیین $$x_0$$، کافی است مکان متناظر با لحظه صفر را در نظر بگیریم.

مثال ۹

فرض کنید شخصی مسافتی به اندازه $$0.5 \ km$$ از مسیر خانه تا اداره پست را در مدت زمان $$9 \ min$$ طی می‌کند. اما ناگهان با یادآوری اینکه چیزی در خانه جا مانده است، در مدت زمان $$9 \ min$$ به سمت خانه بازمی‌گردد. پس از برداشتن بسته، شخص مجددا به سمت اداره پست حرکت می‌کند و این بار مسافت $$1 \ km$$ را در $$15 \ min$$ می‌پیماید. پس از پست کردن بسته، شخص به سمت خانه برمی‌گردد و با عبور از خانه، $$1.75 \ km$$ را در $$25 \ min$$ طی می‌کند. حالا به سوالات زیر پاسخ دهید:

1. کل جابجایی این شخص چقدر است؟
2. اندازه آخرین جابجایی شخص چقدر است؟
3. کل مسافت پیموده شده توسط این شخص چقدر است؟
4. کل سرعت متوسط این شخص چقدر بوده است؟
5. معادله و نمودار مکان - زمان حرکت این شخص را رسم کنید:

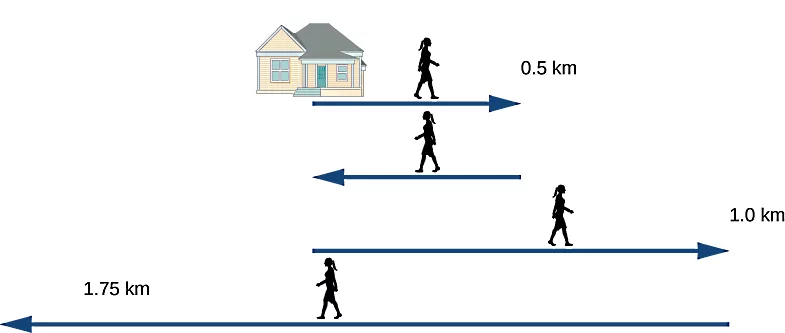
پاسخ

در اولین سوال باید جایجایی کل این شخص در این رفت و آمدها را تعیین کنیم. جابجایی برابر است با اختلاف مکان نهایی و مکان اولیه شخص. این شخص چهار مسیر را مطابق شکل بالا پیموده است. بنابراین اگر جایجایی را برای هر کدام از این مسیرها به‌دست آوریم و با هم جمع کنیم، جابجایی کل محاسبه می‌شود. نکته مهم برای جابجایی این است که این کمیت برداری است، یعنی علاوه بر اندازه، جهت آن هم مهم است و باید در محاسبات لحاظ شود. بنابراین اگر جهت مثبت محور xها را به سمت راست تصویر در نظر بگیریم،  برای جابجایی کل خواهیم داشت:

$$\triangle x_t=\triangle x_1+\triangle x_2+\triangle x_3+\triangle x_4$$

$$\Rightarrow \triangle x_t=0.5 \ km-0.5 \ km+1 \ km-1.75 \ km=-0.75 \ km$$

جابجایی اول و دوم از نظر اندازه با هم برابر هستند، یعنی مسافت پیموده شده در این دو بازه یکی است. اما این دو جابجایی در دو جهت مختلف هستند. بنابراین جابجایی کل این دو بخش معادل صفر است. در جابجایی سوم، شخص به سمت مثبت محور x حرکت کرده است، در حالی که در آخرین جابجایی مسافت بیشتری را در جهت منفی پیموده است. پس انتظار داریم جابجایی کل منفی شود.

در دومین سوال اندازه آخرین جابجایی خواسته شده است. آخرین جابجایی همان $$\triangle x_4$$ است که به‌صورت زیر نشان داده می‌شود:

$$\triangle x_4=-1.75 \ km$$

وقتی صحبت از اندازه می‌شود، باید قدر مطلق بگیریم. پس اندازه این جابجایی که معادل می‌شود با مسافت پیموده شده در این بازه عبارت است از:

$$|\triangle x_4|=|-1.75 \ km|=1.75 \ km$$

در سوال بعدی کل مسافت پیموده شده را باید محاسبه کنیم. در حساب کردن مسافت، به جهت‌ها توجهی نمی‌کنیم. بنابراین با در نظر گرفتن چهار مسیر بالا خواهیم داشت:

$$|\triangle x_t|=|\triangle x_1|+|\triangle x_2|+|\triangle x_3|+|\triangle x_4|$$

$$\Rightarrow |\triangle x_t|=0.5 \ km+0.5 \ km+1 \ km+1.75 \ km=3.75 \ km$$

بنابراین مشخص شد که در این رفت و آمدها با اینکه شخص مسافتی به اندازه $$3.75 \ km$$ را پیموده است، اما در حقیقت جابجایی او برابر است با $$0.75 \ km$$ در جهت منفی محور xها. با داشتن جابجایی کل، می‌توانیم سرعت متوسط کل شخص را در این مسئله با فرمول سرعت متوسط به شکل زیر به‌دست آوریم:

$$v=\frac{\triangle x_t}{\triangle t_t}$$

اما برای محاسبه این سرعت، لازم است ابتدا \triangle t_t را پیدا کنیم که برابر است با:

$$\triangle t_t=9 \ min+9 \ min+15 \ min+25 \ min=58 \ min$$

$$\Rightarrow v=\frac{-0.75 \ km}{58 \ min}=-0.013 \ \frac{ km}{ min}$$

در نهایت باید نمودار مکان - زمان را برای این حرکت رسم کنیم. چهار بازه زمانی مختلف را مطابق جدول زیر در نظر می‌گیریم و برای هر کدام مقدار سرعت متوسط را محاسبه می‌کنیم:

در بازه‌هایی که جابجایی منفی داشتیم، سرعت هم منفی شد. همچنین چون سرعت متوسط در هر کدام از این بازه‌ها مقدار ثابتی است، پس در هر بازه یک حرکت با سرعت ثابت داریم و در نتیجه برای هر کدام یک معادله مکان - زمان مجزا خواهیم داشت:

در نوشتن معادله مکان - زمان یا فرمول سرعت ثابت باید حتما به مقادیر $$x_0$$ برای هر بازه زمانی دقت کنیم. شروع حرکت شخص در هر بازه، از آخرین نقطه مکانی در بازه قبلی است. بنابراین با توجه به اینکه سرعت در تمام بازه‌ها مقدار ثابتی شده است، پس هر بازه از نمودار مکان - زمان ما به شکل یک خط راست خواهد بود. در بازه‌هایی که سرعت مثبت شده است، این خط دارای شیب مثبت است و در بازه‌هایی که سرعت منفی به‌دست آمده است، شیب نمودار هم منفی خواهد بود. چون در این مسئله سرعت صفری حاصل نشد، پس خط موازی با محور زمان با شیب صفر در نمودار نخواهیم داشت:

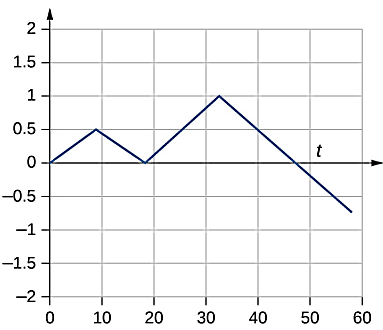
همان‌طور که مشاهده می‌کنید، بازه اول و دوم با اندازه جابجایی و مدت زمان برابر، کاملا شبیه هم اما با دو علامت مختلف برای سرعت در نمودار مشخص شده‌اند. بازه سوم که سرعت مثبت به ما داد، دارای شیب مثبتی است، در حالی که در آخرین جابجایی چون شخص به سمت منفی حرکت کرده است، جابجایی و در نتیجه جهت سرعت منفی شده است.

تمرین ۱

تمرین ۲

تمرین ۳

تمرین ۴

یادگیری سینماتیک برای دانشجویان با فرادرس

یکی از ‌مهم‌ترین عناوین کتاب‌های فیزیک پایه برای دانشجویان رشته مهندسی مبحث سینماتیک است. بنابراین اگر می‌خواهید به این موضوع کاملا مسلط شوید تا در ادامه تحصیلات خود با دانشی که کسب کرده‌اید، درک بهتری نسبت به مفاهیم علوم مهندسی داشته باشید، پیشنهاد ما این است که دوره‌های آموزشی زیر از فرادرس را مشاهده کنید:

1. فیلم آموزش رایگان بردارها در فیزیک ۱ دانشگاهی فرادرس
2. فیلم آموزش فیزیک پایه ۱ فرادرس
3. فیلم آموزش فیزیک ۱ دانشگاهی با رویکرد حل مساله فرادرس
4. فیلم آموزش فیزیک پایه ۱ مرور و حل مساله فرادرس
5. فیلم آموزش فیزیک پایه ۱ مرور و حل تست فرادرس
6. فیلم آموزش رایگان فیزیک پایه ۱ حرکت دورانی فرادرس
7. فیلم آموزش رایگان حرکت ذره در سه بعد در مکانیک تحلیلی فرادرس
8. فیلم آموزش رایگان حرکت در چارچوب نالخت فرادرس
9. فیلم آموزش رایگان سینماتیک ذرات در دینامیک مهندسی فرادرس

به علاوه دو فیلم آموزشی فرادرس با موضوع کاربرد نرم‌افزار و حل مسائل حرکت‌شناسی، شامل موارد زیر هستند:

1. فیلم آموزش رایگان شبیه سازی حرکت یک پرتابه در متلب فرادرس
2. فیلم آموزش حل مسائل فیزیک با پایتون فرادرس

جمع‌بندی

در این نوشته از مجله فرادرس یاد گرفتیم فرمول سرعت ثابت چیست و چگونه می‌توانیم از آن در حل مسائل سینماتیک استفاده کنیم. اما پیش از کاربرد این فرمول‌ها، ابتدا لازم است با مفهوم حرکت با سرعت ثابت آشنا شویم تا بتوانیم آن را به‌درستی تشخیص دهیم. حرکت با سرعت ثابت، بیانگر وضعیت جسم متحرکی است که در حین حرکت، جهت و اندازه سرعتش تغییر نمی‌کند. به عبارت دیگر، در این حرکت سرعت لحظه‌ای با سرعت متوسط برابر است.

از آنجا که عدم تغییر جهت سرعت در کاربرد فرمول سرعت ثابت فاکتور مهمی است، معمولا حرکتی که در راستای یک خط مستقیم با اندازه سرعت ثابتی انجام می‌شود را می‌توانیم همیشه یک حرکت با سرعت ثابت در نظر بگیریم. چنین حرکتی با عنوان حرکت یکنواخت نیز مورد بررسی قرار می‌گیرد. در چنین موقعیت‌هایی، معادله مکان - زمان به شکل $$x=vt+x_0$$ و به‌عنوان اصلی‌ترین فرمول سرعت ثابت، وضعیت حرکت جسم را در طول زمان به‌خوبی توصیف می‌کند.