نمودار سرعت زمان – توضیح به زبان ساده + حل مثال
دونده در مسابقات دو مسافت کوتاه یا بلندی را در مدت زمان مشخصی میدود. او از سرعت صفر شروع به حرکت میکند و تمام تلاش خود را میکند تا با حداکثر سرعت بدود و پس از رسیدن به خط پایان، سرعت او برابر صفر میشود. دونده روی خط مستقیم میدود و اندازه سرعت او با گذشت زمان تغییر میکند. به نمودار تغییرات سرعت برحسب زمان، نمودار سرعت زمان میگوییم. از روی نمودار سرعت زمان، اطلاعات مهمی مانند جابجایی جسم در مدت زمان مشخص و شتاب حرکت آن را میتوانیم بهدست آوریم. در این مطلب، ابتدا نمودار سرعت زمان و انواع آن را به زبان ساده توضیح میدهیم، سپس اطلاعات مربوط به حرکت جسم را از آن بهدست میآوریم.
- یاد میگیرید برای انواع حرکت، نمودار سرعت-زمان را رسم کنید.
- یاد خواهید گرفت ویژگیهای هندسی و تحلیلی نمودار سرعت-زمان را بررسی کنید.
- تمرین میکنید با استفاده از شیب نمودار سرعت-زمان، شتاب را بهدست آورید.
- یاد میگیرید از مساحت زیر نمودار برای بهدست آوردن جابجایی استفاده کنید.
- با نمونههای کاربردی مانند سقوط آزاد و تأثیر مقاومت هوا آشنا میشوید.
- میآموزید اطلاعات مهم حرکت را بهطور مستقیم از نمودار بخوانید.
نمودار سرعت زمان چیست ؟
هر جسم متحرکی با سرعت مشخصی حرکت میکند. سرعت جسم متحرک ممکن است با زمان تغییر کند یا با گذشت زمان ثابت بماند. جدول زیر تغییرات سرعت جسمی را در مدت زمان ۱۰ ثانیه نشان میدهد. سرعت جسم هر یک ثانیه یک بار اندازه گرفته شده است.
| زمان | سرعت جسم برحسب متر بر ثانیه |
| زمان صفر | صفر |
| زمان یک ثانیه | ۲ متر بر ثانیه |
| زمان دو ثانیه | ۴ متر بر ثانیه |
| زمان ۳ ثانیه | ۶ متر بر ثانیه |
| زمان ۴ ثانیه | ۶ متر بر ثانیه |
| زمان ۵ ثانیه | ۶ متر بر ثانیه |
| زمان ۶ ثانیه | ۶ متر بر ثانیه |
| زمان ۷ ثانیه | ۷ متر بر ثانیه |
| زمان ۸ ثانیه | ۸ متر بر ثانیه |
| زمان ۹ ثانیه | ۹ متر بر ثانیه |
| زمان ۱۰ ثانیه | ۱۰ متر بر ثانیه |
آیا میتوانید حرکت جسم را توصیف کنید؟
- جسم از حالت سکون شروع به حرکت میکند، بنابراین در زمان صفر، سرعت اولیه آن برابر صفر است.
- سرعت جسم در فاصله زمانی یک تا ۳ ثانیه از ۲ متر بر ثانیه به ۶ متر بر ثانیه افزایش مییابد.
- جسم در فاصله زمانی ۳ تا ۶ ثانیه با سرعت ثابت ۶ متر بر ثانیه حرکت میکند.
- سرعت جسم در فاصله زمانی ۶ تا ۱۰ ثانیه از ۶ متر بر ثانیه تا ۱۰ متر بر ثانیه افزایش مییابد.
بنابراین، میتوان گفت حرکت جسم به سه بخش تقسیم میشود:
- حرکت با سرعت افزایشی
- حرکت با سرعت ثابت
- حرکت با سرعت افزایشی
اگر میخواهید مفهوم سرعت فاز و سرعت گروه در امواج را بهصورت ساده و رایگان یاد بگیرید و تفاوتها و کاربردهای آنها در انتقال انرژی و اطلاعات را درک کنید، میتوانید آموزش رایگان زیر را مشاهده کنید.
چگونه میتوان نمودار سرعت برحسب زمان را رسم کرد؟ برای رسم هر نموداری در فضای دوبعدی به نقطهای با دو مختصات افقی و عمودی نیاز داریم. در نمودار سرعت زمان، محور عمودی را سرعت و محور افقی را زمان در نظر میگیریم.

در ادامه، جدولی از سرعت برحسب زمان تهیه میکنیم.
| t(s) | |
| 0 | 0 |
| 2 | 1 |
| 4 | 2 |
| 6 | 3 |
| 6 | 4 |
| 6 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | 10 |
نقطههای نشان داده شده در جدول بالا را در نمودار سرعت بر حسب زمان رسم میکنیم.
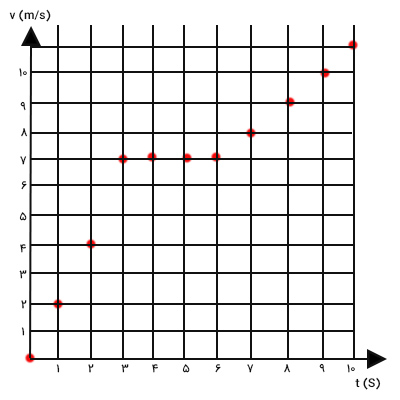
نشان دادن این نقطهها به تنهایی برای رسم نمودار سرعت برحسب زمان کافی نیست. نمودار باید به صورت خط یا منحتی پیوسته رسم شود. نقطههای بالا را به یکدیگر متصل میکنیم.
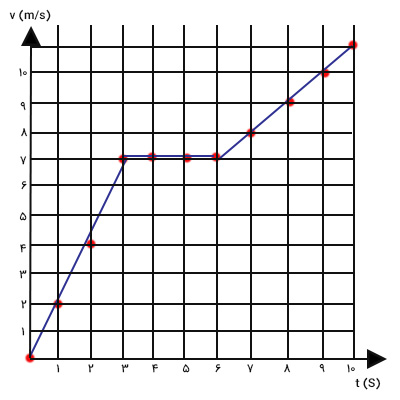
با توجه به توضیحات بالا، نمودار سرعت زمان، تغییرات سرعت جسم برحسب زمان را نشان میدهد. برای رسم تغییرات سرعت برحسب زمان باید تابع سرعت برحسب زمان و نوع حرکت جسم روی خط مستقیم را داشته باشیم. در ادامه، با یکدیگر نمودار سرعت زمان را در حالتهای مختلف رسم و هر یک از نمودارها را با جزییات تحلیل میکنیم.
رسم نمودار سرعت زمان
قبل از آنکه نمودار سرعت زمان جسمی دلخواه را با یکدیگر رسم کنیم، در مورد انواع حرکت روی خط راست و روابط حاکم بر آنها صحبت میکنیم. انواع حرکت روی خط راست عبارت هستند از:
- جسم ساکن است و حرکت نمیکند.
- جسم با سرعت ثابت حرکت میکند. به این حرکت، حرکت با سرعت ثابت میگوییم.
- جسم با شتاب ثابت حرکت میکند و در این حالت سرعت جسم نسبت به زمان تغییر میکند. به این حرکت، حرکت با شتاب ثابت گفته میشود.
- جسم با شتاب متغیر حرکت میکند. در این حالت، شتاب حرکت جسم نسبت به زمان تغییر میکند. به این حرکت، حرکت با شتاب ثابت میگوییم.
نمودار سرعت زمان برای جسم ساکن
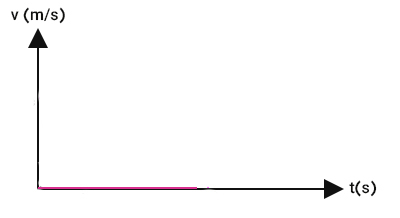
مکان جسم ساکن با گذشت زمان تغییر نمیکند. به بیان دیگر، سرعت جسم ساکن، صفر است و با گذشت زمان مقدار صفر باقی میماند. بنابراین، نمودار سرعت زمان برای جسم ساکن، خطی موازی محور افقی است که از مبدأ میگذرد.
نمودار سرعت زمان در حرکت با سرعت ثابت
هنگامی که جسمی با سرعت ثابت حرکت میکند، مقدار و جهت سرعت آن با گذشت زمان تغییر نخواهد کرد. چرا علاوه بر اندازه، در مورد جهت سرعت نیز صحبت کردیم؟ زیرا سرعت کمیتی برداری است و علاوه بر اندازه، جهت نیز دارد. آیا میدانید نمودار سرعت زمان در این حالت چگونه رسم میشود؟ برای پاسخ به این پرسش، ابتدا معادله حرکت جسم در حرکت با سرعت ثابت را مینویسیم. اگر جسمی با سرعت ثابت در حال حرکت باشد، مکان آن پس از گذشت زمان t با استفاده از رابطه زیر بهدست میآید:
در رابطه فوق:
- مکان جسم در زمان t است.
- سرعت حرکت جسم است.
- مکان اولیه جسم است.
سرعت متوسط به صورت تغییرات جابجایی به مدت زمان این تغییرات و سرعت لحظهای به صورت مشتق مکان نسبت به زمان تعریف میشود. در نتیجه، برای بهدست آوردن رابطه سرعت برحسب زمان در حرکت با سرعت ثابت باید از مکان نسبت به زمان مشتق بگیریم.
همانطور که در رابطه فوق دیده میشود، در حرکت با سرعت ثابت، سرعت نسبت به زمان ثابت است و مقدار آن با گذشت زمان تغییر نمیکند. بنابراین، نمودار سرعت زمان در حرکت با سرعت ثابت، خطی افقی (موازی محور زمان) است که محور عمودی (سرعت) را در نقطه قطع میکند.

نمودار سرعت زمان در حرکت با شتاب ثابت
هنگامی که جسمی با شتاب ثابت حرکت میکند، مقدار و جهت شتاب آن با گذشت زمان تغییر نخواهد کرد. آیا میدانید نمودار سرعت زمان در این حالت چگونه رسم میشود؟ برای پاسخ به این پرسش، ابتدا معادله حرکت جسم در حرکت با شتاب ثابت را مینویسیم. اگر جسمی با شتاب ثابت در حال حرکت باشد، مکان آن پس از گذشت زمان t با استفاده از رابطه زیر بهدست میآید:
در رابطه فوق:
- مکان جسم در زمان t است.
- سرعت اولیه حرکت جسم یا سرعت جسم در ابتدای حرکت است.
- مکان اولیه جسم است.
- شتاب حرکت جسم است که مقدار آن نسبت به زمان ثابت است.
سرعت متوسط به صورت تغییرات جابجایی به مدت زمان این تغییرات و سرعت لحظهای به صورت مشتق مکان نسبت به زمان تعریف میشود. در نتیجه، برای بهدست آوردن رابطه سرعت برحسب زمان در حرکت با شتاب ثابت باید از مکان نسبت به زمان مشتق بگیریم.
همانطور که در رابطه فوق دیده میشود، در حرکت با شتاب ثابت، شتاب نسبت به زمان متغیر است. بنابراین، برای رسم نمودار سرعت زمان در حرکت با شتاب ثابت باید خطی مستقیم با شیب رسم کنیم. اگر شتاب حرکت جسم مثبت باشد، شیب خط مثبت و اگر شتاب حرکت جسم منفی باشد، شیب خط منفی خواهد بود. معادله سرعت برحسب زمان در حرکت با شتاب ثابت همانند معادله خط است که در آن m شیب خط و b عرض از مبدأ است.
توجه به این نکته مهم است که شیب نمودار سرعت زمان، شتاب حرکت جسم را میدهد. برای محاسبه شیب، دو روش را میتوانیم دنبال کنیم.
روش اول محاسبه شیب نمودار سرعت زمان در حرکت با شتاب ثابت
در این روش به دو نقطه روی نمودار نیاز داریم. نمودار سرعت زمان زیر را در نظر بگیرید. دو نقطه A و B روی این نمودار به صورت نشان داده شده در تصویر زیر انتخاب میکنیم.
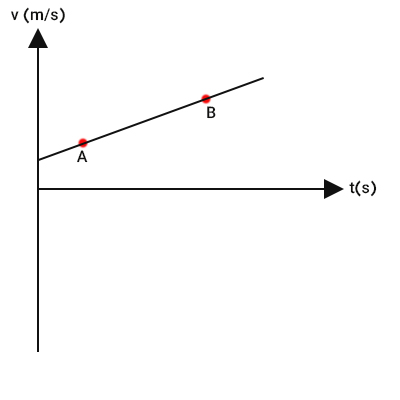
در ادامه، مختصات هر یک از نقطهها را بهدست میآوریم. برای بهدست آوردن مختصات هر نقطه، خطی موازی محور افقی و خطی موازی محور عمودی رسم میکنیم. محل تقاطع خطهای رسم شده با محورهای عمودی و افقی، مختصات هر یک از نقطههای A و B را به ما میدهد. مختصات نقطههای A و B به ترتیب برابر هستند با: و .
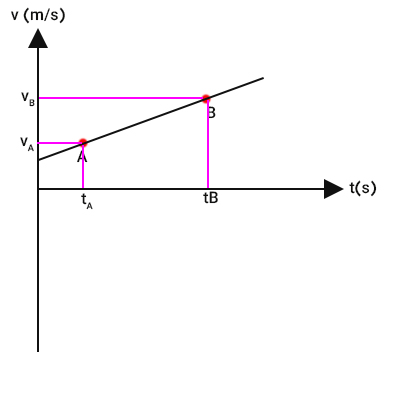
بنابراین، شیب نمودار سرعت زمان برابر است با:
رابطه بالا چه چیزی را نشان میدهد؟ رابطه بالا تغییرات سرعت در بازه زمانی مشخصی را نشان میدهد. همانطور که میدانیم تغییرات سرعت نسبت به زمان برابر مقدار شتاب حرکت جسم است. در نتیجه، شیب نمودار سرعت زمان در بازه زمانی مشخص، شتاب متوسط جسم را به ما میدهد.
روش دوم محاسبه شیب نمودار سرعت زمان در حرکت با شتاب ثابت
از این روش هنگامی میتوانیم استفاده کنیم که معادله سرعت برحسب زمان را داشته باشیم. معادله سرعت زمان در حرکت با شتاب ثابت به صورت زیر نوشته میشود:
به این نکته توجه داشته باشید که رابطه فوق از مشتق مکان نسبت به زمان بهدست میآید. در ادامه، با ذکر چند مثال نمودار سرعت زمان در حرکت با شتاب ثابت را رسم میکنیم.
مثال اول رسم نمودار سرعت زمان در حرکت با شتاب ثابت
اتومبیلی با شتاب ثابت حرکت میکند. تغییرات مکان اتومبیل نسبت به زمان توسط معادله زیر توصیف میشود:
نمودار سرعت زمان این اتومبیل را رسم کنید.
پاسخ
برای رسم نمودار سرعت زمان برای این اتومبیل، ابتدا مشتق مکان را نسبت به زمان بهدست میآوریم:
نمودار سرعت زمان، خطی با معادله با شیب ۴ است. برای رسم این خط، تنها کافی است دو نقطه روی خط را مشخص کنیم. اگر به جای t مقدار صفر را قرار دهیم، سرعت برابر ۳ متر بر ثانیه بهدست میآید. همچنین، اگر به جای t مقدار یک ثانیه را قرار دهیم، مقدار سرعت ۷ متر بر ثانیه بهدست خواهد آمد. در نتیجه، برای رسم نمودار سرعت زمان در این مثال، تنها کافی است خطی گذرنده از دو نقطه و عبور دهیم.
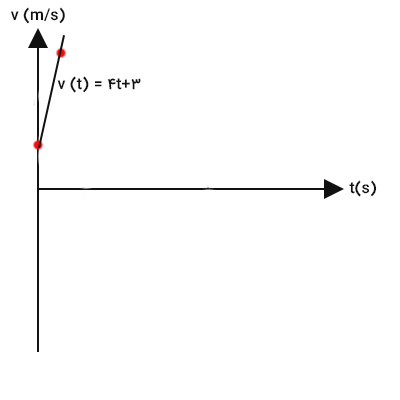
مثال دوم رسم نمودار سرعت زمان در حرکت با شتاب ثابت
فردی با شتاب ثابت در خیابان میدود. تغییرات مکان او نسبت به زمان توسط معادله زیر توصیف میشود:
نمودار سرعت زمان این اتومبیل را رسم کنید.
پاسخ
برای رسم نمودار سرعت زمان برای این اتومبیل، ابتدا مشتق مکان را نسبت به زمان بهدست میآوریم:
نمودار سرعت زمان، خطی با معادله با شیب ۳ است. برای رسم این خط، تنها کافی است دو نقطه روی خط را مشخص کنیم. اگر به جای t مقدار صفر را قرار دهیم، سرعت برابر صفر متر بر ثانیه بهدست میآید. همچنین، اگر به جای t مقدار یک ثانیه را قرار دهیم، مقدار سرعت ۳ متر بر ثانیه بهدست خواهد آمد. در نتیجه، برای رسم نمودار سرعت زمان در این مثال، تنها کافی است خطی گذرنده از دو نقطه و عبور دهیم.
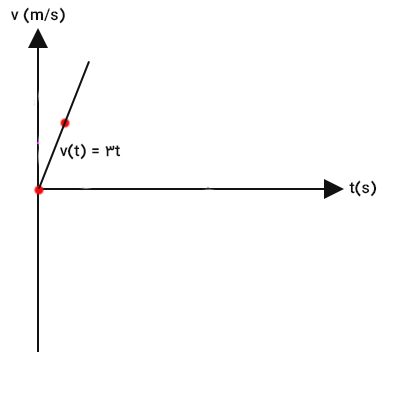
مثال سوم رسم نمودار سرعت زمان در حرکت با شتاب ثابت
فردی در ۲ متری مبدأ قرار دارد و از حالت سکون شروع به حرکت میکند. اگر پس از ۲ ثانیه سرعت او به ۲ متر بر ثانیه برسد. نمودار مکان زمان و سرعت زمان او را رسم کنید.
پاسخ
برای رسم نمودار مکان زمان فرد، ابتدا معادله مکان برحسب زمان او را بهدست میآوریم. نوع حرکت، حرکت با شتاب ثابت و معادله مکان برحسب زمان در حالت کلی به صورت زیر نوشته میشود:
در رابطه فوق:
- شتاب حرکت جسم است.
- مکان اولیه جسم یا مکان جسم در زمان صفر است.
- سرعت اولیه جسم یا سرعت جسم در زمان صفر است.
مکان اولیه و سرعت اولیه قرد به ترتیب برابر ۲ متر و صفر هستند. برای بهدست آوردن شتاب از رابطه زیر استفاده میکنیم:
سرعت اولیه صفر و سرعت در زمان دو ثانیه برابر ۲ متر بر ثانیه است. بنابراین، مقدار شتاب برابر یک متر بر ثانیه بهدست میآید. مقدارهای بهدست آمده را در رابطه مکان برحسب زمان قرار میدهیم:
معادله مکان برحسب زمان به شکل سهمی است. برای رسم این نمودار به نکتههای زیر توجه داشته باشید:
- معادله مکان زمان به شکل است. این معادله از دو جمله و ۲ تشکیل شده است که هر دو مثبت هستند. بنابراین، جسم نمیتواند در مکانهای منفی وجود داشته باشد.
- از آنجا که زمان همواره مثبت است، با دادن مقدارهای صفر، یک و دو به زمان، مکان جسم را بهدست میآوریم.
| زمان (ثانیه) | مکان (متر) |
| صفر | ۲ متر |
| یک | ۲/۵ متر |
| دو | ۴ متر |
سه نقطه بالا را در نمودار مکان زمان به یکدیگر متصل میکنیم. به این نکته توجه داشته باشید که تقعر سهمی همواره به سمت بالا است.
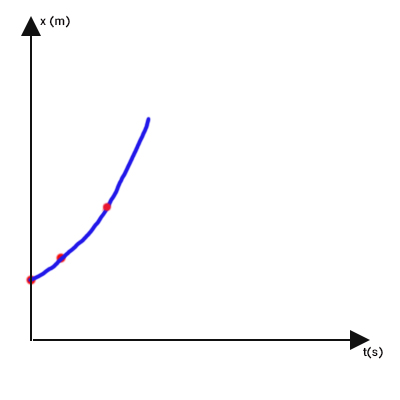
در ادامه، نمودار سرعت زمان را رسم میکنیم. برای رسم نمودار سرعت زمانِ فرد، ابتدا مشتق مکان را نسبت به زمان بهدست میآوریم:
نمودار سرعت زمان، خطی با معادله با شیب یک است. این خط، همان نیمساز ربع اول است.
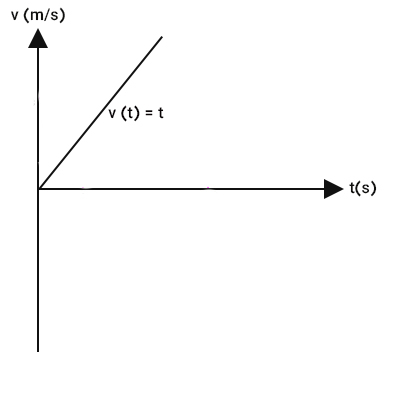
مثال چهارم رسم نمودار سرعت زمان در حرکت با شتاب ثابت
اتومبیلی با سرعت ۳۰ متر بر ثانیه در خیابانی در حال حرکت است که ناگهان به ایستگاه پلیس میرسد. پلیس بلافاصله از راننده میخواهد تا متوقف شود. راننده ترمز میکند و با شتاب ثابتی پس از ۵ ثانیه متوقف میشود. نمودار سرعت زمان اتومبیل را از لحظه ترمز تا توقف کامل رسم کنید.
پاسخ
همانطور که در مطالب بالا اشاره شد نمودار سرعت زمان، نموداری را نشان میدهد که در آن سرعت روی محور عمودی و زمان روی محور افقی قرار دارند. برای رسم این نمودار ابتدا محورهای عمودی و افقی را رسم و آنها را نامگذاری میکنیم.

در ادامه، محورهای مختصات را به صورت نشان داده شده در تصویر زیر درجهبندی میکنیم. به این نکته توجه داشته باشید که اتومبیل در مدت زمان ۵ ثانیه به طور کامل متوقف میشود و سرعت آن از ۳۰ متر بر ثانیه به صفر میرسد. از اینرو، محور زمان را تا ۵ ثانیه با گام یک ثانیه و محور سرعت را تا ۳۰ متر بر ثانیه با گام ۱۰ متر بر ثانیه تقسیم میکنیم.
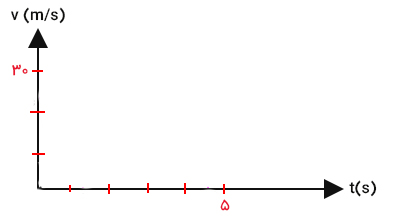
برای رسم نمودار سرعت زمان این اتومبیل باید به چند نکته توجه داشته باشیم:
- بر طبق صورت مسئله، اتومبیل پس از هشدار پلیس ترمز میکند و با شتاب ثابت متوقف میشود. بنابراین، نوع حرکت، حرکت با شتاب ثابت است و نمودار مکان زمان در این حرکت خطی مستقیم با شیب مثبت یا منفی است. منفی یا مثبت بودن شیب به علامت شتاب بستگی دارد.
- از آنجا که نمودار سرعت زمان، خطی مستقیم با شیب ثابت است، برای رسم آن داشتن دو نقطه و اتصال آنها به یکدیگر کافی است.
- زمان صفر را لحظهای در نظر میگیریم که راننده ترمز میکند. در این لحظه سرعت اتومبیل برابر ۳۰ متر بر ثانیه است. بنابراین، مختصات نقطه اول برابر خواهد بود.
- اتومبیل ۵ ثانیه پس از ترمز به طور کامل متوقف میشود. در نتیجه، در زمان ۵ ثانیه، سرعت اتومبیل برابر صفر است. از اینرو، مختصات نقطه دوم برابر خواهد بود.
- دو نقطه را مشخص و آنها را به صورت نشان داده شده در تصویر زیر به یکدیگر متصل میکنیم.
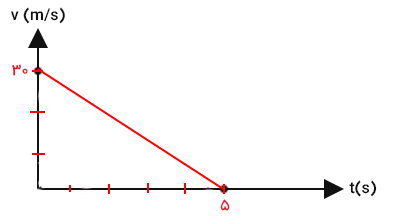
آیا میدانید اتومبیل با چه شتابی متوقف میشود؟ برای بهدست آوردن شتاب باید شیب نمودار سرعت زمان را بهدست آوریم. نمودار، خطی مستقیم با شیب منفی است که از دو نقطه و میگذرد. این دو نقطه را به شکل زیر نامگذاری میکنیم.
شیب خط گذرنده از دو نقطه فوق با استفاده از رابطه زیر بهدست میآید:
با قرار دادن مقدارهای داده شده در مثال در رابطه بالا، شیب نمودار مکان زمان یا همان شتاب ترمز اتومبیل را بهدست میآوریم:
در نتیجه، اتومبیل با شتاب ۶- متر بر مجذورثانیه در مدت زمان ۵ ثانیه متوقف میشود. شاید از خود بپرسید معادله سرعت برحسب زمان را چگونه میتوان بهدست آورد. معادله سرعت زمان در حرکت با شتاب ثابت به صورت کلی زیر نوشته میشود:
در رابطه بالا، و به ترتیب شتاب حرکت و سرعت اولیه جسم هستند. شتاب حرکت را برابر ۶- متر بر مجذورثانیه بهدست آوردیم. همچنین، سرعت اتومبیل در لحظه ترمز برابر ۳۰ متر بر ثانیه است. بنابراین، معادله سرعت برحسب زمان به صورت زیر نوشته میشود:
نمودار سرعت زمان در حرکت با شتاب متغیر
در حرکت با شتاب متغیر، شتاب حرکت جسم نسبت به زمان تغییر میکند. از آنجا که شیب نمودار سرعت زمان، شتاب حرکت جسم را به ما میدهد، این نمودار در حرکت با شتاب متغیر، خط افقی یا خطی مستقیم با شتاب ثابت نیست. بلکه نموداری منحنی با شتاب متغیر خواهد بود. به این نکته توجه داشته باشید که اگر شتاب حرکت در هر لحظه از زمان تغییر کند، نمودار سرعت زمان، منحنی با شیب متغیر است. اما اگر شتاب حرکت در بازه زمانی مشخصی ثابت باشد و پس از آن تغییر کند، نمودار سرعت زمان خطهایی مستقیم با شیبهای متغیر است. برای درک بهتر این موضوع به دو مثال زیر توجه کنید.
مثال ۱
نمودار سرعت زمان داده شده در تصویر زیر را در نظر بگیرید.
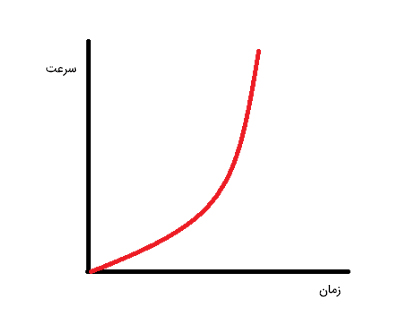
همانطور که مشاهده میشود، نمودار خط راست یا افقی نیست، بلکه منحنی با شیب متغیر است. برای بهدست آوردن شیب منحنی در هر نقطه، خطی مماس بر منحنی در آن نقطه رسم میکنیم. شیب مماس بر منحنی در سه نقطه رسم شده است. شیب و بنابراین شتاب حرکت در هر سه نقطه متفاوت و افزایشی است.
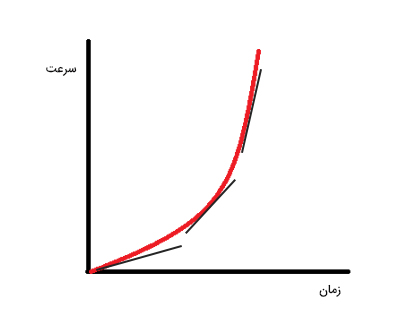
مثال ۲
اتومبیلی را در نظر بگیرید که از سرعت صفر با شتاب ثابت شروع به حرکت میکند و پس از مدت زمان ۵ ثانیه سرعت آن به ۴۵ متر بر ثانیه میرسد. در ادامه، اتومبیل در مدت زمان ۲۵ ثانیه با همین سرعت حرکت میکند تا اینکه راننده با هشدار پلیس ترمز و پس از ۱۰ ثانیه با شتاب ثابت متوقف میشود. نمودار سرعت زمان اتومبیل را رسم کنید.
پاسخ
در این مثال، شتاب حرکت اتومبیل در سه مرحله تغییر کرده است، اما در هر مرحله شتاب حرکت ثابت باقی میماند. حرکت اتومبیل از سه مرحله تشکیل شده است، که در هر مرحله نمودار سرعت زمان را جداگانه رسم میکنیم.
- مرحله اول: اتومبیل از حالت سکون شروع به حرکت میکند و سرعت آن پس از مدت زمان ۵ ثانیه به ۴۵ متر بر ثانیه میرسد. از آنجا که این افزایش سرعت با شتاب ثابت انجام گرفته، نمودار سرعت زمان خطی مستقیم است که از دو نقطه و میگذرد.
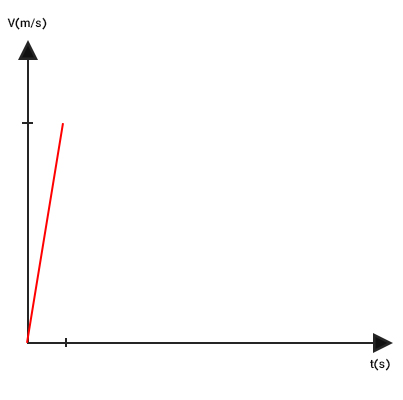
- مرحله دوم: سپس، اتومبیل به مدت ۲۵ ثانیه با سرعت ۴۵ متر بر ثانیه به حرکت خود ادامه میدهد. در این مرحله، اتومبیل با سرعت ثابت حرکت میکند و شتاب حرکت آن برابر صفر است. از اینرو، نمودار سرعت زمان خطی افقی است که از نقطه میگذرد.
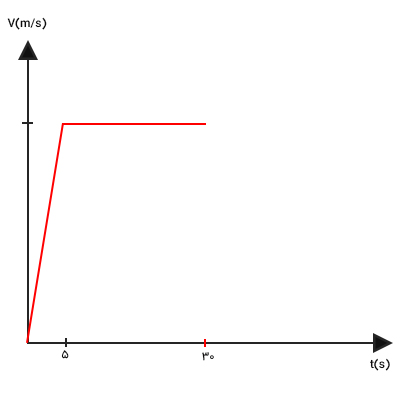
- مرحله سوم: در مرحله آخر، راننده اتومبیل با هشدار پلیس ترمز میکند و در مدت زمان ۱۰ ثانیه با شتاب ثابت به طور کامل متوقف میشود. از آنجا که این کاهش سرعت با شتاب ثابت انجام گرفته، نمودار سرعت زمان خطی مستقیم است که از دو نقطه و میگذرد.
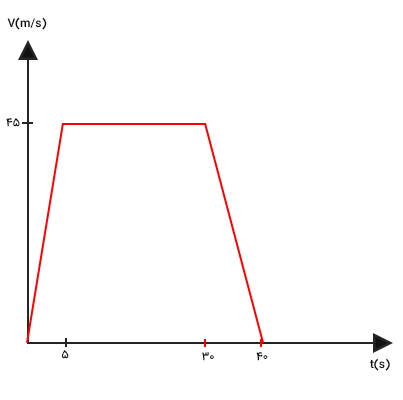
پرسش ۱: شتاب حرکت در مرحله اول را بهدست آورید.
پاسخ: برای بهدست آوردن شتاب باید شیب نمودار سرعت زمان را بهدست آوریم. نمودار خطی مستقیم با شیب مثبت است که از دو نقطه و میگذرد. این دو نقطه را به شکل زیر نامگذاری میکنیم.
شیب خط گذرنده از دو نقطه فوق با استفاده از رابطه زیر بهدست میآید:
با قرار دادن مقدارهای داده شده در مثال در رابطه بالا، شیب نمودار مکان زمان یا همان شتاب ترمز اتومبیل را بهدست میآوریم:
پرسش ۲: شتاب حرکت در مرحله سوم را بهدست آورید.
پاسخ: برای بهدست آوردن شتاب باید شیب نمودار سرعت زمان را بهدست آوریم. نمودار خطی مستقیم با شیب منفی است که از دو نقطه و میگذرد. شیب خط گذرنده از دو نقطه فوق با استفاده از رابطه زیر بهدست میآید:
با قرار دادن مقدارهای داده شده در مثال در رابطه بالا، شیب نمودار مکان زمان یا همان شتاب ترمز اتومبیل را بهدست میآوریم:
نکته ۱: اگر سرعت جسمی با گذشت زمان با آهنگ ثابتی افزایش یابد، نمودار سرعت زمان خطی مستقیم با شیب مثبت است.
نکته ۲: اگر سرعت جسمی با گذشت زمان با آهنگ ثابتی کاهش یابد، نمودار سرعت زمان خطی مستقیم با شیب منفی است.
تحلیل نمودار سرعت زمان
در بخش قبل یاد گرفتیم چگونه نمودار سرعت برحسب زمان را رسم کنیم. اگر جسم با سرعت ثابت و شتاب صفر حرکت کند، نمودار سرعت زمان خطی افقی، موازی محور زمان است. اگر جسم با شتاب ثابت حرکت کند، این نمودار خطی مستقیم با شیب مثبت یا منفی خواهد بود. بنابراین، با داشتن نمودار سرعت زمان و محاسبه شیب آن میتوانیم شتاب حرکت جسم را بهدست آوریم. سوال دیگری که ممکن است مطرح شود آن است که آیا اطلاعات دیگری نیز میتوان از نمودار سرعت زمان بهدست آورد، بله.
مساحت زیر نمودار سرعت زمان چیست ؟
با استفاده از مساحت زیر نمودار سرعت زمان میتوان جابجایی جسم را بهدست آورد. کودک نوپایی را در نظر بگیرید که به تازگی شروع به راه رفتن کرده است. نمودار سرعت زمان این کودک به صورت نشان داده شده در تصویر زیر است.
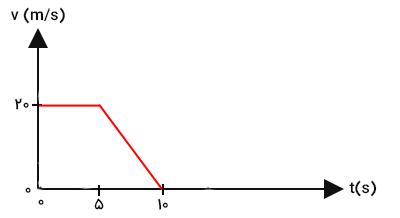
چگونه میتوانیم با استفاده از نمودار فوق، مقدار جابجایی کودک را بهدست آوریم؟ نمودار سرعت زمان، سرعت جسم را در هر لحظه از زمان به ما میدهد. نگاه کردن به این نمودار همانند نگاه کردن به سرعتسنج است. نمودار فوق چه اطلاعاتی به ما میدهد؟
- با نگاه کردن به نمودار میدانیم سرعت کودک در زمان صفر برابر ۲۰ متر بر ثانیه است.
- با گذشت زمان کودک با سرعت ثابت ۲۰ متر بر ثانیه حرکت میکند.
- سرعت حرکت کودک تا زمان ۵ ثانیه ثابت باقی میماند.
- پس از زمان ۵ ثانیه، سرعت کودک کاهش مییابد و پس از ۱۰ ثانیه از شروع حرکت به صفر میرسد.
سرعت برابر جابجایی بر مدت زمان لازم برای انجام جابجایی است. بنابراین، جابجایی برابر حاصلضرب سرعت در زمان خواهد بود.
سرعت × زمان = جابجایی
از رابطه بالا هنگامی میتوانیم استفاده کنیم که جسم با سرعت ثابت حرکت کند. کودک در ۵ ثانیه اول حرکت با سرعت ثابت ۲۰ متر بر ثانیه حرکت میکند، بنابراین جابجایی او برابر ۵×۲۰ یعنی ۱۰۰ متر است. از اینرو، هنگامی که جسمی با سرعت ثابت حرکت میکند، جابجایی آن را به راحتی میتوانیم بهدست آوریم. مشکل هنگامی ایجاد میشود که جسم با شتاب ثابت و سرعت متغیر حرکت میکند. بخش دوم حرکت کودک نیز بدین صورت است. شاید با خود فکر کنید در این مرحله نیز میتوانیم از رابطه «سرعت × زمان = جابجایی» استفاده کنیم. اما اینگونه نیست.
به این نکته توجه داشته باشید که در ۵ ثانیه دوم حرکت کودک، سرعت او ثابت نیست و با گذشت زمان تغییر میکند. بنابراین، نمیتوانیم از رابطه «سرعت × زمان = جابجایی» برای محاسبه جابجایی استفاده کنیم. در ادامه، در این مورد صحبت خواهیم کرد. مقدار جابجایی کودک را در ۵ ثانیه اول حرکت برابر ۱۰۰ متر بهدست آوردیم. ۱۰۰ متر از حاصلضرب سرعت در جابجایی بهدست آمد. آیا میدانید معنای این حاصلضرب چیست؟ معنای ۲۰ متر بر ثانیه در نمودار سرعت زمان چیست؟ بخش حرکت با سرعت ثابت را توسط خطی عمودی از بخش حرکت با شتاب ثابت جدا میکنیم.
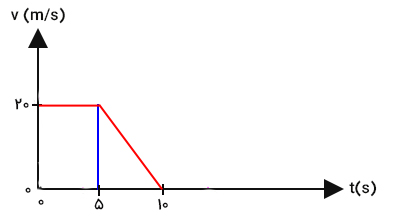
با تقسیم کردن نمودار سرعت زمان به دو بخش، بخش اول مستطیلی به طول ۲۰ و عرض ۵ و بخش دوم مثلثی با ارتفاع ۲۰ و قاعده ۵ است. بنابراین، ۲۰ طول مستطیل تشکیل شده در بخش اول است. مساحت مستطیل برابر حاصلضرب طول در عرض آن است. بنابراین، مساحت مستطیل تشکیل شده برابر حاصلضرب ۲۰ در ۵ یعنی ۱۰۰ خواهد بود. در واقع ۱۰۰ همان مساحت زیر نمودار سرعت زمان در ۵ ثانیه اول حرکت کودک است. به بیان دیگر، جابجایی در ۵ ثانیه اول حرکت کودک برابر مساحت زیر نمودار سرعت زمان خواهد بود.
در نتیجه، برای آنکه بتوانیم جابجایی جسمی را در مدت زمان مشخصی بهدست آوریم، تنها کافی است مساحت زیر نمودار سرعت زمان آن را در بازه زمانی مشخص شده حساب کنیم. به طور مشابه، برای آنکه بدانیم کودک در ۵ ثانیه دوم حرکت چه مقدار جابجا شده است، مساحت زیر نمودار سرعت زمان را در این بازه زمانی بهدست میآوریم. با توجه به نمودار سرعت زمان در تصویر بالا، مساحت زیر نمودار در ۵ ثانیه دوم حرکت برابر مساحت مثلثی با ارتفاع ۲۰ و قاعده ۵ خواهد بود. بنابراین، جابجایی کودک در ۵ ثانیه دوم حرکت برابر است با:
جابجایی کل در مدت زمان ۱۰ ثانیه چه مقدار است؟ کودک در مدت زمان ۱۰ ثانیه به اندازه ۱۵۰ متر جابجا میشود، ۱۰۰ متر در ۵ ثانیه اول و ۵۰ متر در ۵ ثانیه دوم حرکت.
نکته: جابجایی کل را میتوان از مساحت کل زیر نمودار سرعت زمان نیز بهدست آورد. به عنوان مثال، شکل زیرِ نمودارِ سرعت زمانِ کودک، ذوزنقهای به ارتفاع ۲۰ و دو قاعده با اندازههای ۵ و ۱۰ است. مساحت ذوزنقه با استفاده از رابطه زیر بهدست میآید:
در رابطه فوق، a و b قاعدههای ذوزنقه و h ارتفاع ذوزنقه است. با قرار دادن مقدارهای قاعده و ارتفاع در رابطه بالا، مساحت ذوزنقه برابر ۱۵۰ بهدست میآید. در نتیجه، جابجایی کودک در دو مرحله برابر ۱۵۰ متر است.
مثال اول مساحت زیر نمودار سرعت زمان
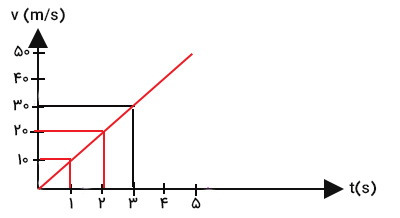
نمودار سرعت زمان جسمی در ادامه رسم شده است. جابجایی جسم در فاصله زمانی ۲ تا ۴ ثانیه چه مقدار است؟
پاسخ
نخستین سوالی که برای حل این مثال باید به آن پاسخ دهیم آن است که نوع حرکت چیست. با توجه به نمودار نشان داده شده در بالا، نمودار سرعت زمان خطی مستقیم با شیب ثابت است. از آنجا شتاب حرکت جسم برابر شیب نمودار سرعت زمان است، جسم با شتاب ثابت روی خط مستقیم حرکت میکند. در این مثال باید جابجایی جسم در بازه زمان ۲ تا ۴ ثانیه را بهدست آوریم. برای انجام این کار، تنها کافی است مساحت زیر نمودار سرعت زمان را در این بازه محاسبه کنیم.
مساحت زیر نمودار سرعت زمان در بازه زمانی خواسته شده در تصویر زیر نشان داده شده است. شکل نشان داده شده چیست؟ ذوزنقه. بنابراین، برای محاسبه جابجایی جسم در بازه زمانی خواسته شده باید مساحت ذوزنقهای با دو قاعده ۲۰ و ۴۰ و ارتفاع دو را بهدست آوریم.
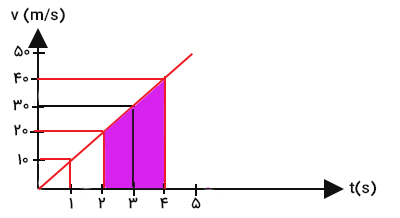
مساحت ذوزنقه موردنظر برابر است با:
در نتیجه، جسم در بازه زمانی ۲ تا ۴ ثانیه ۶۰ متر جابجا میشود.
پرسش: جابجایی جسم در ۵ ثانیه اول حرکت چه مقدار است؟
پاسخ: برای محاسبه جابجایی در ۵ ثانیه اول حرکت، ابتدا مساحت زیر نمودار سرعت زمان را در این بازه زمانی مشخص میکنیم.
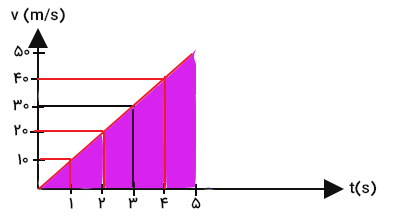
با توجه به تصویر بالا، برای محاسبه جابجایی جسم در ۵ ثانیه اول حرکت باید مساحت مثلثی به ارتفاع ۵ و قاعده ۵۰ را بهدست آوریم.
مثال دوم مساحت زیر نمودار سرعت زمان
نمودار سرعت زمان آسانسوری در ادامه نشان داده شده است. آسانسور ابتدا در حال سکون است، سپس در مدت ۳ ثانیه سرعت آن از صفر به ۳ متر بر ثانیه میرسد و به مدت ۱۵ ثانیه با این سرعت حرکت میکند و در پایان، آسانسور در مدت ۵ ثانیه متوقف میشود و سرعت آن از ۳ متر بر ثانیه به صفر میرسد. جابجایی آسانسور را در بازه زمانی نشان داده شده بهدست آورید.
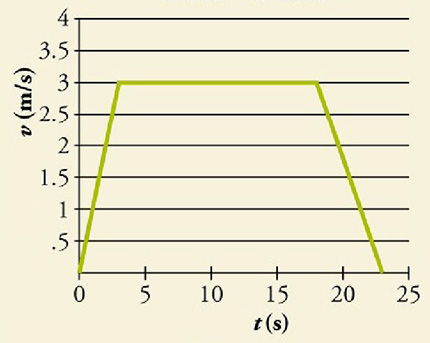
پاسخ
برای محاسبه جابجایی آسانسور در مدت حرکت، باید زمان، کل حرکت را بدانیم. حرکت به سه مرحله تقسیم میشود:
- حرکت با شتاب ثابت: در این مرحله آسانسور از حالت سکون شروع به حرکت میکند و پس از ۳ ثانیه سرعت آن به ۳ متر بر ثانیه میرسد. بنابراین، نمودار سرعت زمان خطی مستقیم با شتاب مثبت است.
- حرکت با سرعت ثابت: در این مرحله آسانسور به مدت ۱۵ ثانیه با سرعت ثابت ۳ متر بر ثانیه به حرکت خود ادامه میدهد. از اینرو، نمودار سرعت زمان خطی افقی با شیب صفر است.
- حرکت با شتاب ثابت: در این مرحله آسانسور در مدت زمان ۵ ثانیه با شتاب ثابت متوقف میشود و سرعت آن از ۳ متر بر ثانیه به صفر میرسد. در نتیجه، نمودار سرعت زمان خطی مستقیم با شتاب منفی است.
مدت زمانِ کلِ حرکت برابر است با:
۳ + ۱۵ + ۵ = مدت زمان کل حرکت
بنابریان، مدت زمان کل حرکت برابر ۲۳ ثانیه است. برای محاسبه جابجایی کل در این مدت باید مساحت زیر نمودار سرعت زمان را بهدست آوریم. شکل زیر نمودار سرعت زمان ذوزنقهای با دو قاعده ۲۳ و ۱۸ و ارتفاع ۳ است. بنابراین، مساحت آن برابر است با:
پرسش: آسانسور در ۱۰ ثانیه اول حرکت چه مقدار جابجا میشود؟
پاسخ: برای محاسبه جابجایی آسانسور در ۱۰ ثانیه اول حرکت، ابتدا مساحت زیر نمودار سرعت زمان را در این بازه زمانی مشخص میکنیم.
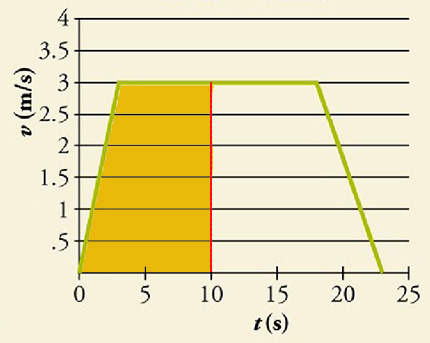
در نتیجه، برای محاسبه جابجایی در این بازه زمانی باید مساحت ذوزنقهای با قاعدههای ۱۰ و ۷ و ارتفاع ۳ را بهدست آوریم:
مثال سوم مساحت زیر نمودار سرعت زمان
نمودار سرعت زمان اتومبیلی در مدت زمان ۵۰ ثانیه رسم شده است. جابجایی اتومبیل در این مدت زمان را بهدست آورید.
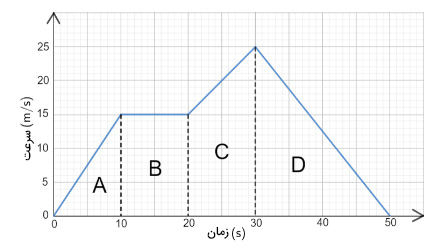
پاسخ
برای محاسبه جابجایی اتومبیل در ۵۰ ثانیه باید مساحت زیر نمودار سرعت زمان را بهدست آوریم. همانطور که در تصویر بالا دیده میشود برای محاسبه این مساحت، باید نمودار سرعت زمان را به چهار قسمت تقسیم کنیم. به بیان دیگر، حرکت اتومبیل نیز در ۵۰ ثانیه به چهار قسمت تقسیم میشود:
- حرکت با شتاب ثابت: در این مرحله، اتومبیل از حالت سکون شروع به حرکت میکند و پس از ۱۰ ثانیه سرعت آن به ۱۵ متر بر ثانیه میرسد. بنابراین، نمودار سرعت زمان خطی مستقیم با شتاب مثبت است. در این حالت، مساحت زیر نمودار برابر مساحت مثلثی به ارتفاع ۱۵ و قاعده ۱۰ است.
- حرکت با سرعت ثابت: در این مرحله، اتومبیل به مدت ۱۰ ثانیه با سرعت ثابت ۱۵ متر بر ثانیه به حرکت خود ادامه میدهد. از اینرو، نمودار سرعت زمان خطی افقی با شیب صفر است. در این حالت، مساحت زیر نمودار برابر مساحت مستطیلی به طول ۱۵ و عرض ۱۰ است.
- حرکت با شتاب ثابت: در این مرحله، سرعتِ اتومبیل در مدت زمان ۱۰ ثانیه با شتاب ثابت افزایش مییابد و از ۱۵ متر بر ثانیه به ۲۵ متر بر ثانیه میرسد. در نتیجه، نمودار سرعت زمان خطی مستقیم با شتاب مثبت است. در این حالت، مساحت زیر نمودار برابر مساحت ذوزنقهای به ارتفاع ۱۰ و قاعدههای ۱۵ و ۲۵ است.
- حرکت با شتاب ثابت: در این مرحله، اتومبیل در مدت زمان ۲۰ ثانیه با شتاب ثابت متوقف میشود و سرعت آن از ۳ متر بر ثانیه به صفر میرسد. در نتیجه، نمودار سرعت زمان خطی مستقیم با شتاب منفی است. در این حالت، مساحت زیر نمودار برابر مساحت مثلثی به ارتفاع ۲۵ و قاعده ۲۰ است.
در نتیجه، جابجایی کل برابر مجموع جابجایی هر مرحله و برابر ۶۷۵ متر است.
مثال چهارم مساحت زیر نمودار سرعت زمان
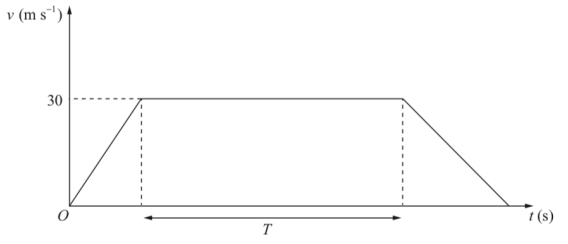
نمودار سرعت زمان حرکت قطاری بین دو ایستگاه در تصویر زیر رسم شده است. قطار در مدت زمان T ثانیه ۲ کیلومتر حرکت میکند. مقدار T را بهدست آورید.
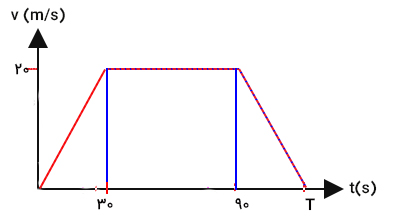
پاسخ
جابجایی قطار بین دو ایستگاه برابر ۲ کیلومتر است. به بیان دیگر، مساحت زیر نمودار سرعت زمان داده شده برابر ۲ کیلومتر خواهد بود. بنابراین، برای بهدست آوردن T تنها کافی است که مساحت زیر نمودار داده شده را بهدست آوریم و آن را برابر ۲ کیلومتر قرار دهیم. مساحت زیر نمودار سرعت زمان برابر مساحت ذوزنقهای به ارتفاع ۲۰ و قاعدههای T و ۶۰ است. مساحت ذوزنقه برابر است با:
مساحت زیر نمودار سرعت زمان برابر جابجایی قطار و برابر ۲ کیلومتر است:
مثال پنجم مساحت زیر نمودار سرعت زمان
دوندهای در مسابقه دو مسافت ۲۰۰ متر را در مدت زمان ۲۰/۳۲ ثانیه طی میکند. نمودار سرعت زمان او در ادامه رسم شده است.
- سرعت بیشینه او در طول مسابقه را بهدست آورید.
- مسافت طی شده توسط دونده در ۵ ثانیه ابتدای مسابقه را بهدست آورید.
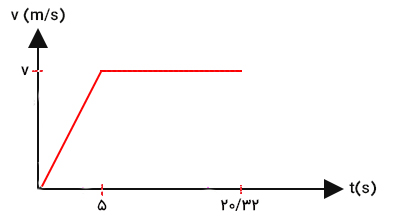
پاسخ
ابتدا سرعت بیشینه دونده به هنگام دویدن را محاسبه میکنیم. برای انجام این کار مساحت زیر نمودار سرعت زمانِ دونده را بهدست میآوریم و آن را برابر ۲۰۰ (مسافت کل طی شده توسط دونده) قرار میدهیم. مساحت زیر نمودار سرعت زمان برابر مساحت ذوزنهای به ارتفاع و قاعدههای ۲۰/۳۲ و ۱۵/۳۲ است:
مساحت زیر نمودار سرعت زمان برابر مسافت طی شده توسط دونده و برابر ۲۰۰ متر است:
در ادامه، مسافت طی شده توسط دونده در ۵ ثانیه ابتدای حرکت را بهدست میآوریم. مسافت طی شده در این مدت توسط دونده برابر مساحت زیر نمودار سرعت زمان یعنی مساحت مثلثی به ارتفاع ۱۱/۲۲ و قاعده ۵ است:
در نتیجه، دونده در ۵ ثانیه اول حرکت مسافتی برابر ۲۸/۳ متر را طی میکند.
مثال ششم مساحت زیر نمودار سرعت زمان
موتورسواری از خانه شروع به حرکت میکند و وارد خیابان اصلی میشود. او در ۸ ثانیه اول حرکت سرعت خود را با شتاب ثابت از صفر تا ۱۲ متر بر ثانیه افزایش میدهد و پس از آن به مدت ۱۵ ثانیه با سرعت ثابت به حرکت خود ادامه میدهد. پس از ۱۵ ثانیه ناگهان گربهای به وسط خیابان میدود. موتورسوار برای آنکه با گربه تصادف نکند، بلافاصله ترمز میکند و با شتاب ثابت متوقف میشود. اگر مدت زمان کلِ حرکت موتورسوار برابر ۲۶ ثانیه باشد، نمودار سرعت زمان، موتورسوار را رسم و مسافت کل طی شده توسط او را از شروع حرکت تا توقف کامل محاسبه کنید.
پاسخ
ابتدا نمودار سرعت زمان موتورسوار را رسم میکنیم. با توجه به صورت مسئله حرکت موتورسوار به سه بخش تقسیم میشود:
- در ۸ ثانیه اول حرکت، سرعت موتورسوار از صفر با شتاب ثابت به ۱۲ متر بر ثانیه میرسد. بنابراین، نمودار سرعت زمان در این قسمت خطی مستقیم با شیب مثبت است، زیرا سرعت افزایش مییابد.
- در ادامه، موتورسوار به مدت ۱۵ ثانیه با سرعت ثابت حرکت میکند. در این حالت، نمودار سرعت زمان خطی افقی با شیب صفر است.
- در پایان، موتورسوار با دیدن گربه ترمز میکند و با شتاب ثابت میایستد. از آنجا که مدت زمان کلِ حرکت برابر ۲۶ ثانیه و مدت زمان دو مرحله اول برابر ۲۳ ثانیه است، موتور پس از ۳ ثانیه به طور کامل متوقف میشود.
در نتیجه، نمودار سرعت زمان در مرحله اول حرکت خطی گذرنده از دو نقطه و است. در مرحله دوم، نمودار خطی افقی گذرنده از نقطه و در مرحله سوم خطی مستقیم و گذرنده از دو نقطه و خواهد بود.
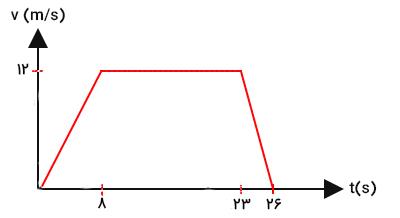
مسافت طی شده توسط موتورسوار برابر مساحت زیر نمودار سرعت زمان و مساحت ذوزنقهای با قاعدههای ۲۶ و ۱۵ و ارتفاع ۱۲ است:
مثال هفتم مساحت زیر نمودار سرعت زمان
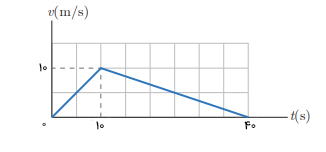
متحرکی در امتداد محور حرکت میکند. نمودار سرعت زمان این متحرک در ادامه نشان داده شده است. سرعت متوسط متحرک در بازه زمانی صفر تا ۵ ثانیه چند برابر سرعت متوسط آن در بازه زمانی ۲۵ تا ۴۰ ثانیه است؟
پاسخ
قبل از حل این مثال باید بدانیم سرعت متوسط چگونه با استفاده از نمودار بهدست میآید. برای محاسبه سرعت متوسط در بازه زمانی مشخص با استفاده از نمودار ابتدا مساحت زیر نمودار را در این بازه بهدست میآوریم، سپس مقدار بهدست آمده را بر بازه زمانی تقسیم میکنیم.
ابتدا سرعت متوسط را در بازه زمانی صفر تا ۵ ثانیه بهدست میآوریم. مساحت زیر نمودار سرعت زمان در این بازه زمانی برابر مساحت مثلثی با قاعده و ارتفاع ۵ است:
از اینرو، سرعت متوسط در این بازه زمان برابر است. به طور مشابه، سرعت متوسط را در بازه زمانی ۲۵ تا ۴۰ ثانیه بهدست میآوریم. مساحت زیر نمودار سرعت زمان در این بازه زمانی برابر مساحت مثلثی با قاعده ۱۵ و ارتفاع ۵ است:
بنابراین، سرعت متوسط در این بازه زمان برابر است. در نتیجه، سرعت متوسط در بازه زمانی صفر تا ۵ ثانیه برابر سرعت متوسط در بازه زمانی ۲۵ تا ۴۰ ثانیه خواهد بود.
مثال هشتم مساحت زیر نمودار سرعت زمان
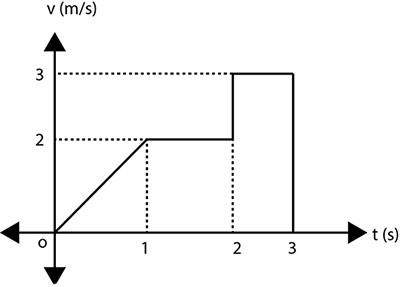
نمودار جسمی در تصویر زیر نشان داده شده است. سرعت متوسط در مدت زمان ۳ ثانیه را بهدست آورید.
پاسخ
برای محاسبه سرعت متوسط باید مساحت زیر نمودار سرعت زمان را بر بازه زمانی تقسیم کنیم. بنابراین، سرعت متوسط را میتوان با استفاده از نمودار سرعت زمان از رابطه زیر بهدست آوریم:
برای محاسبه مساحت زیر نمودار سرعت زمان باید مساحت دو مستطیل و یک مثلث را بهدست آوریم.
- مساحت مثلث: قاعده و ارتفاع مثلث به ترتیب برابر یک و ۲ هستند، بنابراین مساحت آن برابر یک خواهد بود.
- مساحت مستطیل در بازه زمانی یک تا دو ثانیه: طول و عرض مستطیل به ترتیب برابر ۲ و یک هستند، بنابراین مساحت آن برابر ۲ خواهد بود.
- مساحت مستطیل در بازه زمانی ۲ تا ۳ ثانیه: طول و عرض مستطیل به ترتیب برابر ۳ و یک هستند، بنابراین مساحت آن برابر ۳ خواهد بود.
در نتیجه، جابجایی کل برابر ۶ متر و سرعت متوسط برابر است.
شیب نمودار سرعت زمان چیست ؟
شیب نمودار سرعت زمان، شتاب حرکت را به ما میدهد. نمودار یوزپلنگی در تصویر زیر رسم شده است.
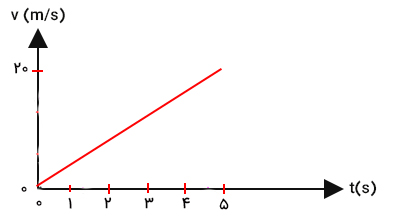
همانطور که در بخشهای قبل بیان شد نمودار سرعت زمان، سرعت جسم را در هر لحظه از زمان به ما میدهد. این نمودار همانند سرعتسنج اتومبیل است. تفاوت اصلی نمودار سرعت زمان با سرعتسنج اتومبیل آن است که این نمودار نهتنها سرعت را در هر لحظه از زمان به ما میدهد، بلکه به ما میگوید جسم در چه جهتی حرکت میکند. چگونه نمودار جهت حرکت جسم را به ما میدهد؟ اگر نمودار همانند نمودار نشان داده شده در تصویر بالا مثبت باشد، در این حالت میتوانیم بگوییم جسم در جهت مثبت قراردادی حرکت میکند.
در حالت کلی و به هنگام حل مسائل حرکت روی خط راست، جهت راست یا جهت بالا را به صورت قراردادی، جهت مثبت انتخاب میکنیم. اگر نمودار زیر محور زمان باشد، در این حالت جهت سرعت جسم در جهت منفی، چپ یا پایین، خواهد بود. در نتیجه، نمودار سرعت زمان به ما اندازه و جهت سرعت را میدهد. بر طبق نمودار سرعت زمان، سرعت یوزپلنگ در زمان صفر برابر صفر است و با گذشت زمان افزایش مییابد و پس از گذشت ۵ ثانیه سرعت او به ۲۰ متر بر ثانیه میرسد.
با گذشت زمان سرعت یوزپلنگ افزایش مییابد، این به چه معنا است؟ افزایش یا کاهش سرعت با گذشتت زمان به معنای شتابدار بودن حرکت جسم است. به بیان دیگر، هرگاه سرعت حرکت جسمی افزایش یا کاهش یابد، جسم با شتاب حرکت میکند. شتاب حرکت را میتوان با محاسبه شیب نمودار بهدست آورد. در حالت کلی، شتاب برابر تغییرات سرعت برحسب زمان است.
یا توجه به نمودار سرعت زمان، یوزپلنگ، شتاب او را در مدت زمان ۵ ثانیه بهدست میآوریم. زمان اولیه صفر و زمان نهایی ۵ ثانیه و بر طبق نمودار، سرعت در زمان صفر برابر صفر و در زمان ۵ ثانیه برابر ۲۰ متر بر ثانیه است. بنابراین، شتاب یوزپلنگ برابر است با:
در نتیجه، سرعت یوزپلنگ هر ثانیه ۴ متر بر ثانیه افزایش مییابد. در ادامه، فرض کنید پلنگی دنبال یوزپلنگ شروع به دویدن میکند. نمودار سرعت زمان پلنگ به صورت زیر، همراه با نمودار یوزپلنگ رسم شده است.
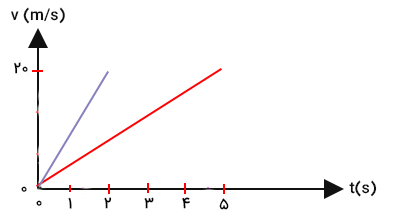
با توجه به نمودار فوق متوجه میشویم که پلنگ نیز با شتاب مشخصی حرکت میکند. آیا میدانید مقدار شتاب آن چه مقدار است؟ آیا شتاب پلنگ بزرگتر از شتاب یوزپلنگ است؟ سرعت پلنگ در زمان صفر برابر صفر و ۲ ثانیه بعد به ۲۰ متر بر ثانیه میرسد، بنابراین شتاب حرکت پلنگ برابر است با:
پلنگ با شتاب بیشتری نسبت به یوزپلنگ حرکت میکند. با توجه به نمودار بالا، سرعت یوزپلنگ در مدت ۵ ثانیه از صفر به ۲۰ متر بر ثانیه میرسد، در حالیکه سرعت پلنگ در زمان ۲ ثانیه به این مقدار خواهد رسید. از اینرو، پلنگ با شتاب بزرگتری حرکت میکند. آیا پلنگ از یوزپلنگ جلو میزند؟ نمیدانیم، زیرا نمودار سرعت زمان هیچ چیزی در مورد مکانهای اولیه پلنگ و یوزپلنگ به ما نمیگوید. نمودارهای سرعت زمان پلنگ و یوزپلنگ چه تفاوتی با یکدیگر دارند؟
نمودار پلنگ شیب تندتری نسبت به نمودار سرعت زمانِ یوزپلنگ دارد، زیرا پلنگ با شتاب بزرگتری در مقایسه با یوزپلنگ حرکت میکند. به بیان دیگر، هرچه شیب نمودار جسمی بیشتر باشد، جسم با شتاب بزرگتری حرکت خواهد کرد. اگر نمودار سرعت زمانِ جسمی خطی مستقیم با شیب ثابت باشد، جسم در همه زمانها با شتاب ثابت حرکت میکند. هر چه شیب خط بزرگتر باشد، شتاب حرکت بزرگتر خواهد بود.
نمودار سرعت زمان سقوط آزاد
در حرکت سقوط آزاد جسم از ارتفاع مشخصی نسبت به سطح زمین، رها میشود. بنابراین سرعت اولیه آن صفر است و تحت جاذبه زمین سقوط میکند. حرکت جسم سقوطکننده را میتوان با استفاده از نمودارهای حرکت برحسب زمان، مانند نمودارهای سرعت زمان و مکان زمان، توصیف کرد. در این بخش، نمودار سقوط آزاد را با یکدیگر رسم میکنیم. قبل از رسم نمودار، معادلههای مکان زمان و سرعت زمان جسم رها شده را مینویسیم:
هنگامی که جسمی از ارتفاع مشخصی رها میشود تحت جاذبه زمین آزادانه سقوط میکند. در این حرکت، شتاب ثابتی به دلیل نیروی جاذبه زمین بر جسم اعمال میشود. به این شتاب، شتاب جاذبه میگوییم. بنابراین، در حرکت سقوط آزاد، جسم از ارتفاع مشخصی رها میشود و تحتتاثیر جاذبه زمین سقوط میکند. هنگام رها شدن، نیروی گرانش زمین بر جسم وارد و آن را به سمت مرکز زمین میکشاند. بر طبق قوانین نیوتن، هرگاه نیرویی بر جسمی وارد شود، جسم با شتاب مشخص و ثابتی حرکت میکند. در حرکت سقوط آزاد، شتاب جسم سقوطکننده همان شتاب جاذبه زمین است.
حرکت با شتاب ثابت بدان معنا است که سرعت جسم متحرک با آهنگ ثابتی افزایش مییابد. از آنجا که شتاب جسم سقوط کننده ثابت و برابر g است، نمودار سرعت زمان باید خطی با شیب ثابت و منفی باشد.
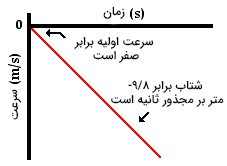
همانطور که در مطالب بالا اشاره شد اگر نمودار سرعت زمان خطی باشد، متحرک با شتاب ثابت حرکت میکند. از آنجا که جسم در حرکت سقوط آزاد تحت جاذبه رو به پایینِ ۹/۸ متر بر مجذور ثانیه زمین سقوط میکند، نمودار سرعت زمان خطی مستقیم با شتاب ثابت است. با توجه به نمودار رسم شده متوجه میشویم که جسم با سرعت صفر شروع به حرکت میکند و سرعت آن پس از مدت زمان مشخصی به مقدار منفی و بزرگی میرسد. این بدان معنا است که جسم در جهت منفی حرکت میکند و سرعت آن افزایش مییابد.
به این نکته توجه داشته باشید که در حرکت بر خط مستقیم، جهت راست و بالا را به طور معمول، جهت مثبت انتخاب میکنیم. بنابراین، اگر جسمی در خلاف این جهتها حرکت کند، شتاب یا سرعت آن را منفی در نظر میگیریم. در حرکت سقوط آزاد، جسم به سمت پایین پرتاب میشود و جهت سرعت و شتاب آن منفی است. در نتیجه، علامت آنها منفی در نظر گرفته میشود. شیبِ ثابت و منفی نشاندهنده شتاب منفی و ثابت است.
نمودار سرعت زمان چترباز
در این قسمت نمودار سرعت زمان چترباز را با یکدیگر رسم میکنیم. هواپیمایی از زمین بلند و چتربازی برای پریدن از ارتفاع مشخصی سوار هواپیما میشود. گرچه هواپیما با سرعت ثابتی حرکت میکند، اما چترباز داخل هواپیما ساکن است. پس از مدتی، چترباز برای پریدن آماده میشود و لبه هواپیما مینشیند. در این حالت، دو نیرو بر شخص وارد میشود:
- نیروی وزن به سمت پایین
- نیروی وارد شده از طرف هواپیما به سمت بالا
مجموع برایند نیروهای وارد شده بر چترباز صفر و او ساکن است.

بنابراین، در اولین مرحله و قبل از پریدن چترباز از هواپیما، سرعت او برابر صفر است. از اینرو، نمودار سرعت زمان او خطی افقی روی محور زمان است.

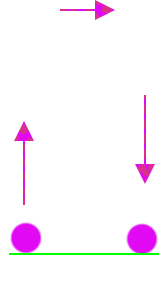
هنگامیکه چترباز از هواپیما بیرون میپرد، شتاب میگیرید و سرعت او افزایش مییابد. در ابتدا، شتاب در بیشترین حالت خود قرار دارد. وزن چترباز قبل و پس از پرش تغییر نمیکند، بنابراین نیروی وزن به سمت پایین ثابت میماند. پس از پرش، علاوه بر نیروی وزن، نیروی مقاومت هوا به سمت بالا بر چترباز وارد میشود. پس از پرش و در ابتدا، نیرویی به سمت پایین بر چترباز وارد میشود، زیرا نیروی وزن بزرگتر از نیروی مقاومت هوا است. بنابراین، ابتدای پرش، اندازه شتاب بیشینه خواهد بود. پس از پرش نمودار سرعت زمان به صورت نشان داده در تصویر زیر است.
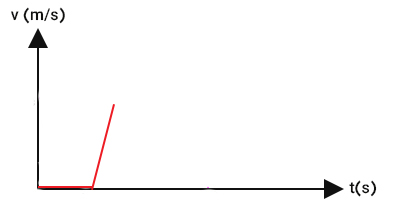
از آنجا که نیروی مقاومت هوا به سرعت جسم بستگی دارد، با افزایش سرعت چترباز، اندازه این نیرو افزایش مییابد. بنابراین، اندازه برایند نیرو به سمت پایین و شتاب کاهش مییابند. با کاهش شتاب، شیب نمودار سرعت زمان نیز کاهش خواهد یافت.
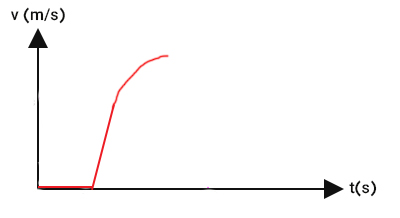
با گذشت زمان و افزایش نیروی مقاومت هوا، اندازه این نیرو برابر نیروی وزن میشود. در نتیجه، برایند نیروهای وارد شده بر چترباز، صفر و هیچ نیرویی بر او وارد نمیشود. صفر بودن نیرو به معنای صفر بودن شتاب است. بنابراین، شتاب حرکت چترباز برابر صفر میشود. از اینرو، چترباز با سرعت ثابت سقوط میکند. در این حالت، نمودار سرعت زمان خطی افقی موازی محور زمان است.
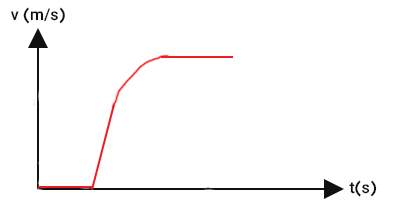
در این حالت، سرعت چترباز به سرعت حد میرسد. بنابراین، در سرعت حد، برایند نیروهای وارد بر چترباز برابر صفر است و او با سرعت حد سقوط میکند. هنگامیکه چترِ چترباز باز میشود، مقاومت هوا افزایش مییابد. به بیان دیگر، نیرو وزن در جهت پایین ثابت میماند، اما نیروی مقاومت هوا در جهت بالا افزایش مییابد. در نتیجه، برایند نیروهای وارد شده به چترباز به سمت بالا خواهد بود. از اینرو، سرعت و شتاب چترباز کاهش مییابد. این حالت تا رسیدن سرعت چترباز به سرعت حدِ جدید ادامه مییابد.
پس از کاهش شتاب، چترباز با سرعتی در حدود ۵ متر بر ثانیه حرکت میکند. ۵ متر بر ثانیه، سرعت حدِ جدید چترباز است. بنابراین، پس از باز شدن چتر و افزایش نیروی مقاومت هوا در جهت بالا، سرعت و شتاب چترباز تا رسیدن سرعت به سرعتِ حدِ جدید کاهش مییابند.
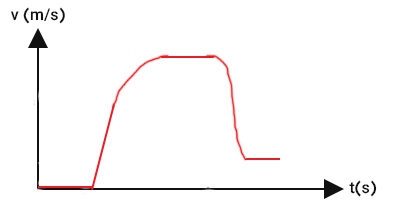
چترباز پس از رسیدن به سرعت ثابت روی زمین مینشیند. پس از رسیدن به زمین، نیرویی از سمت زمین و رو به بالا بر چترباز وارد میشود. به همین دلیل، سرعت چترباز کاهش مییابد و پس از مدتی به طور کامل متوقف میشود. در این حالت، سرعت با آهنگ زیاد کاهش مییابد. بنابراین، نمودار سرعت زمان، خطی با شیب زیاد خواهد بود.
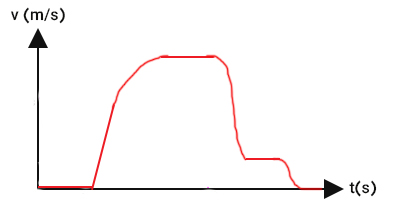
تمرین و آزمون

نکات نمودار سرعت زمان
تا اینجا میدانیم نمودار سرعت زمان چیست و چه اطلاعاتی را میتوانیم از آن بهدست آوریم. قبل از حل مسائل مختلف در مورد این مبحث، نکتههای مهم در مورد نمودار سرعت زمان را بار دیگر به طور خلاصه با یکدیگر مرور میکنیم.
تعریف نمودار سرعت زمان چیست ؟
نمودار سرعت زمان، سرعت جسم را برحسب زمان به هنگام حرکت آن روی خط راست نشان میدهد. سرعت روی محور عمودی و زمان روی محور زمان نشان داده میشوند. نمودار سرعت زمان میتواند برای سرعتهای منفی نیز رسم شود. از آنجا که سرعت، کمیتی برداری است، علاوه بر اندازه، جهت نیز دارد. بنابراین، برای سرعتهای منفی، نمودار زیر محور زمان رسم میشود.
نکات اصلی نمودار سرعت زمان چیست ؟
با استفاده از نمودار سرعت زمان میتوانیم اطلاعات مهمی را در مورد حرکت جسم بهدست آوریم:
- شیب نمودار برابر شتاب حرکت جسم است.
- خط مستقیم نشان میدهد که جسم با آهنگ ثابتی شتاب میگیرد.
- خط افقی و موازی محور زمان نشان میدهد که جسم با سرعت ثابت حرکت میکند.
- مساحت زیر نمودار سرعت زمان (ناحیه بین نمودار و محور افقی) جابجایی جسم را به ما میدهد.
- اگر نمودار بالای محور زمان باشد، جسم به سمت جلو حرکت میکند.
- اگر نمودار زیرِ محور زمان باشد، جسم در جهت منفی حرکت میکند.
- جابجایی کل جسم از نقطه مبدأ برابر مجموع نواحی بالایی محور زمان و نواحی زیر محور زمان است.
- جابجایی کل طی شده توسط جسم برابر مجموع تمام مساحتها است.
- اگر نمودار محور افقی (محور زمان) را در هر لحظه قطع کند، جسم در آن لحظه ساکن است.
- اگر نمودار بالای محور افقی باشد، جسم با سرعت مثبت در جهت مثبت قراردادی حرکت میکند.
- اگر نمودار پایینِ محور افقی باشد، جسم با سرعت منفی در جهت منفی قراردادی حرکت میکند.
مثال ۱
با توجه به نکتههای گفته شده در بالا، نمودار سرعت زمان نشان داده شده در تصویر زیر را تحلیل کنید.

پاسخ
هر یک از بخشهای نمودار را به صورت جداگانه و با استفاده از نکتههای گفته شده تحلیل میکنیم:
- بخش ۱: سرعت اولیه را نشان میدهد. این قسمت نشان میدهد که جسم با سرعت اولیه غیرصفر شروع به حرکت کرده است.
- بخش ۲: نمودار خطی مستقیم با شیب مثبت است. بنابراین، سرعت جسم با شتاب ثابت و مثبت افزایش مییابد.
- بخش ۳: در این قسمت، نمودار خط نیست، بلکه منحنی با تقعر به سمت بالا است. از آنجا که شیب خط مماس بر این قسمت از نمودار با گذشت زمان تغییر میکند، جسم با شتاب متغیر به حرکت خود ادامه میدهد.
- بخش ۴: در ادامه و با افزایش سرعت تا مقداری مشخص، جسم با سرعت ثابت به حرکت خود ادامه میدهد. از اینرو، نمودار خطی افقی با شیب صفر است.
- بخش ۵: در این بخش، نمودار خطی مستقیم با شیب منفی است. این بدان معنا است که سرعت جسم با شتاب منفی و ثابت کاهش مییابد، تا جایی که به صفر میرسد. در این بخش، جسم هنوز در راستای مثبت حرکت میکند.
- بخش ۶: سرعت جسم در یک لحظه برابر صفر میشود.
- بخش ۷: نمودار، زیرِ محور زمان رسم شده و خطی مستقیم با شیب منفی است. این بدان معنا است که سرعت جسم در جهت منفی با شتاب منفی و ثابت افزایش مییابد. به بیان دیگر، جسم با شتاب ثابت در خلاف جهت مثبت حرکت میکند.
- بخش ۸: جسم پس از حرکت با شتاب ثابت در جهت منفی، تغییر جهت میدهد و سرعت آن کاهش مییابد.
- بخش ۹: مساحت زیر نمودار سرعت زمان یا جابجایی جسم در جهت مثبت را نشان میدهد.
- بخش ۱۰: مساحت زیر نمودار سرعت زمان یا جابجایی جسم در جهت منفی را نشان میدهد.
نمونه سوال سرعت زمان
پس از آشنایی با نمودار سرعت زمان و یادگیری نکتههای مهم این نمودار، در ادامه چند سوال در این زمینه را با یکدیگر حل میکنیم.
سوال ۱
حرکت پرندهای که روی خط مستقیم پرواز میکند به مدت ۶۰ ثانیه ردیابی شد. با توجه به اطلاعات بهدست آمده در این بازه زمانی، نمودار سرعت زمان پرنده به صورت زیر رسم شده است.
- شتاب پرنده را در ۲۰ ثانیه اول حرکت بهدست آورید.
- مسافت طی شده توسط پرنده در ۲۸ ثانیه اول حرکت را محاسبه کنید.
- جابجایی پرنده را از ابتدای حرکت تا پایان آن بهدست آورید.
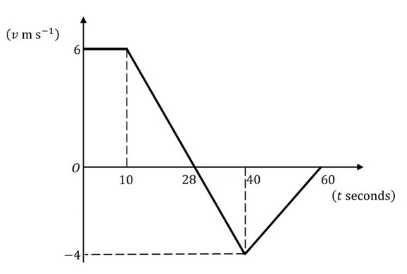
پاسخ
با توجه به نکات گفته شده، شیب نمودار سرعت زمان، شتاب حرکت را به ما میدهد. در قسمت اول میخواهیم شتاب پرنده را در ۲۰ ثانیه اول حرکت بهدست آوریم. پرنده از ثانیه صفر تا ۱۰ با سرعت ثابت ۶ متر بر ثانیه پرواز میکند، بنابراین شتاب حرکت او برابر صفر است. سپس، سرعت خود را با شتاب منفی و ثابت کاهش میدهد تا به صفر برسد. برای محاسبه شتاب پس از ۱۰ ثانیه باید شیب خط را بهدست آوریم. خط از نقطههای و میگذرد، بنابراین شیب خط یا شتاب پرنده تا ۲۰ ثانیه برابر است با:
در قسمت دوم مسافت طی شده توسط پرنده را در ۲۸ ثانیه اول حرکت بهدست میآوریم. برای انجام این کار ابتدا شکلِ زیرِ نمودار سرعت زمان تا زمان گفته شده مشخص میکنیم.
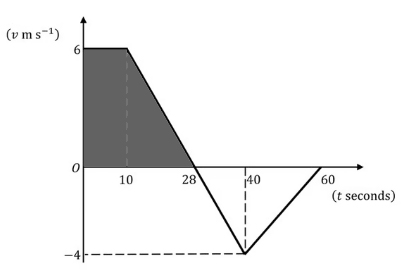
با توجه به قسمت رنگ شده در تصویر بالا، برای محاسبه مسافت طی شده توسط پرنده در ۲۸ ثانیه اول حرکت باید مساحت ذوزنقهای با قاعدههای ۲۸ و ۱۰ و ارتفاع ۶ را بهدست آوریم:
در قسمت سوم سوال جابجایی کل پرنده را در ۶۰ ثانیه بهدست میآوریم. در بخش دوم، مسافت طی شده توسط پرنده در ۲۸ ثانیه اول حرکت را بهدست آوردیم. پرنده پس از ۲۸ ثانیه در جهت منفی شروع به حرکت میکند. از ثانیه ۲۸ به بعد نمودار سرعت زمان، زیرِ محور افقی است. بنابراین، برای بهدست آوردن جابجایی پرنده باید مساحت این قسمت را از مساحت قسمت قبل کم کنیم. مسافت طی شده توسط پرنده در جهت منفی برابر مساحت مثلثی به ارتفاه ۴ و قاعده ۳۲ است:
بنابراین، مسافت طی شده توسط پرنده در جهت منفی برابر ۶۴ متر و جابجایی کل در ۶۰ ثانیه برابر متر است.
سوال ۲
ماشین اسباببازی را کف سالن ورزشی قرار میدهیم. این ماشین روی خط راست و از حالت سکون شروع به حرکت میکند و با شتاب ثابت به حرکت خود ادامه میدهد و در مدت ۴ ثانیه سرعت آن به ۵ متر بر ثانیه میرسد. سپس با شتاب ثابت یک متر بر مجذور ثانیه به مدت ۲ ثانیه، سرعت خود را کاهش میدهد.
- نمودار سرعت زمان ماشین اسباببازی را رسم کنید.
- مسافت کل طی شده توسط ماشین را محاسبه کنید.
پاسخ
ابتدا نمودار را رسم میکنیم. حرکت ماشین از دو بخش تشکیل شده است:
- از حالت سکون شروع به حرکت میکند و سرعت آن با شتاب ثابت پس از ۴ ثانیه به ۵ متر بر ثانیه میرسد. در این حالت نمودار سرعت زمان خطی مستقیم با شیب مثبت و ثابت است.
- سرعت ماشین به مدت دو ثانیه با شتاب ثابت یک متر بر مجذور ثانیه کاهش مییابد و در این حالت نیز نمودار خطی مستقیم با شیب ۱- است.
برای رسم نمودار سرعت زمان از بخش اول حرکت شروع میکنیم. در این قسمت، نمودار خطی مستقیم با شیب ۱/۲۵ است. به بیان دیگر، ماشین اسباببازی با شتاب ثابت ۱/۲۵ متر بر مجذور ثانیه حرکت میکند.
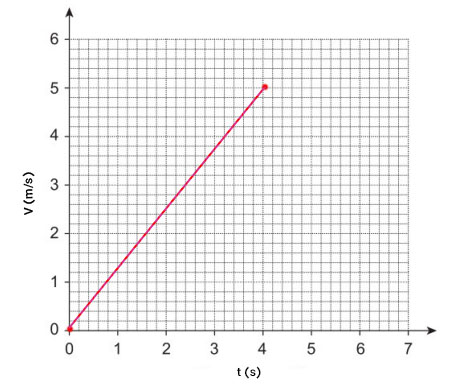
در ادامه، سرعت ماشین با شتاب یک متر بر مجذور ثانیه به مدت دو ثانیه کاهش مییابد. آیا میدانید سرعت ماشین پس از ۲ ثانیه چه مقداری دارد؟ شتاب یک متر بر مجذور ثانیه بدان معنا است که هر ثانیه یک متر بر ثانیه از سرعت ماشین کاسته میشود، بنابراین سرعت آن پس از ۲ ثانیه به ۳ متر بر ثانیه میرسد.
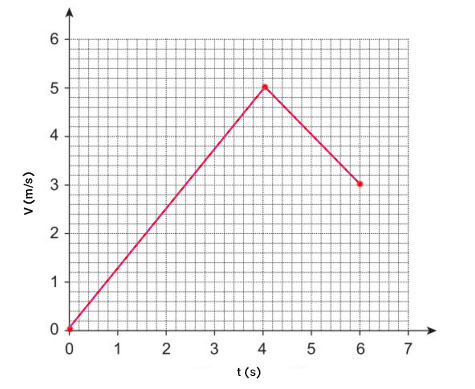
در بخش دوم باید مسافت کل طی شده توسط ماشین اسباببازی را محاسبه کنیم. برای انجام این کار مساحت زیر نمودار سرعت زمان را بهدست میآوریم. برای انجام این کار، زیرِ نمودار را به دو بخش تقسیم میکنیم:
- مثلثی با ارتفاع ۵ و قاعده ۴.
- ذوزنقههای با قاعدههای ۵ و ۳ و ارتفاع ۲.
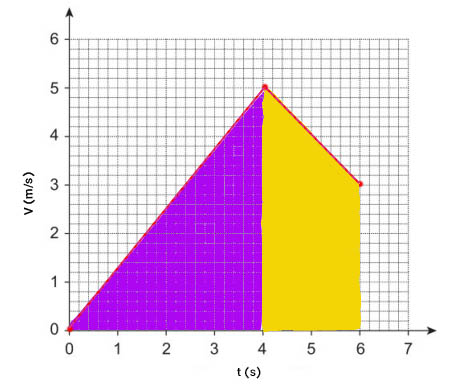
مساحت قسمت بنفشرنگ برابر است با:
بنابراین، ماشین اسباببازی در بخش اول حرکت ۱۰ متر جابجا میشود. مساحت قسمت زردرنگ برابر است با:
ماشین در ادامه حرکت، ۸ متر جابجا میشود. بنابراین، مسافت، کل طی شده توسط او برابر ۱۸ متر است.
سوال ۳
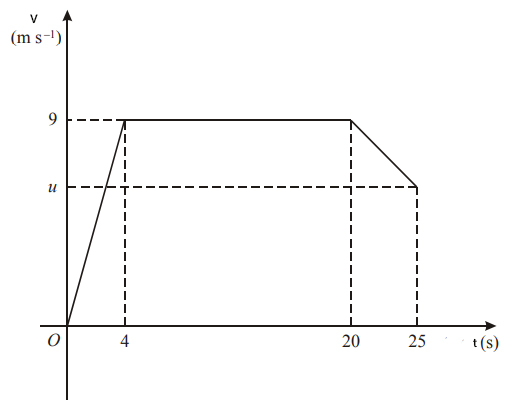
دوندهای در مسابقه دوی ۲۰۰ متر شرکت و مسافت ۲۰۰ متری را در مدت زمان ۲۵ ثانیه طی میکند. نمودار دونده در تصویر زیر نشان داده شده است. مطلوب است:
- شتاب دونده در ۴ ثانیه ابتدای مسابقه.
- مسافت طی شده توسط دونده در ۲۰ ثانیه ابتدای مسابقه.
- مقدار .
پاسخ
همانطور که در مطالب بالا اشاره شد، شیب نمودار ، شتاب حرکت جسم را به ما میدهد. برای بهدست آوردن شتاب دونده در ۴ ثانیه ابتدای مسابقه، شیب نمودار سرعت زمان را در این بازه زمانی بهدست میآوریم. نمودار در این بازه زمانی، خطی با شیب ثابت و مثبت است که از نقطههای و میگذرد:
برای آنکه بدانیم دونده در ۲۰ ثانیه ابتدای مسابقه چه مقدار میدود باید مساحت زیر نمودار که ذوزنقهای با قاعدههای ۲۰ و ۱۶ و ارتفاع ۹ است را بهدست آوریم:
بنابراین، دونده در مدت ۲۰ ثانیه از مسابقه، مسافت ۱۶۲ متر را میدود. در بخش آخر، مقدار را بهدست میآوریم. دونده در مدت ۲۵ ثانیه ۲۰۰ متر میدود و در ۲۰ ثانیه ۱۶۲ متر دویده است. بنابراین، در ۵ ثانیه باقیمانده از مسابقه ۳۸ متر میدود. این مسافت برابر مساحت زیر نمودار سرعت زمان دونده است که در تصویر زیر مشاهده میکنیم.
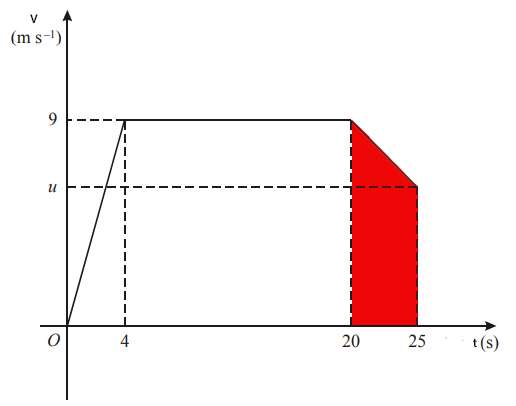
مساحت قسمت قرمزرنگ برابر است با:
از آنجا که مسافت طی شده توسط دونده در ۵ ثانیه پایانی مسابقه برابر ۳۷ متر است، مقدار نیز برابر ۳۸ خواهد بود:
سوال ۴
جسمی روی خط راست حرکت میکند. نمودار سرعت زمان آن به صورت نشان داده شده در تصویر زیر است. حرکت جسم را توصیف کنید.

پاسخ
شیب نمودار سرعت زمان، شتاب حرکت جسم را به ما میدهد. نمودار نشان داده شده در تصویر بالا خطی نیست، بنابراین شیب آن با گذشت زمان تغییر میکند. شیب منحنی غیرخطی در هر نقطه برابر شیب خط مماس بر آن نقطه است. برای آنکه تغییر شتاب بر حسب زمان را بدانیم شیب خط مماس بر چند نقطه روی نمودار را با یکدیگر بررسی میکنیم.
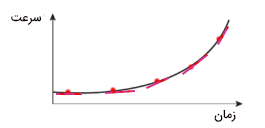
همانطور که در تصویر بالا دیده میشود شیب خطهای مماس بر نمودار سرعت زمان با گذشت زمان افزایش مییابند. بنابراین، شتاب جسم با گذشت زمان افزایش خواهد یافت. به بیان دیگر، جسم با شتاب افزایشی حرکت میکند. همچنین، سرعت جسم نیز با گذشت زمان افزایش مییابد. بنابراین، حرکت جسم تندشونده است.
سوال ۵
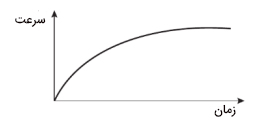
جسمی روی خط راست حرکت میکند. نمودار سرعت زمان آن به صورت نشان داده شده در تصویر زیر است. حرکت جسم را توصیف کنید.
پاسخ
برای آنکه تغییر شتاب بر حسب زمان را بدانیم شیب خط مماس بر چند نقطه روی نمودار را با یکدیگر بررسی میکنیم. همانطور که در تصویر زیر دیده میشود شیب خطهای مماس بر نمودار سرعت زمان با گذشت زمان کاهش مییابند. بنابراین، شتاب جسم با گذشت زمان کاهش خواهد یافت. به بیان دیگر، جسم با شتاب کاهشی حرکت میکند. همچنین، سرعت جسم نیز با گذشت زمان افزایش مییابد. بنابراین، حرکت جسم کندشونده است.

سوال ۶
توپ کوچکی با سرعت متر بر ثانیه به صورت عمودی از سطح زمین به سمت بالا پرتاب میشود و پس از ۴ ثانیه به سطح زمین بازمیگردد. نمودار سرعت زمان توپ در مدت ۴ ثانیه را رسم کنید.
پاسخ
توپ با سرعت اولیه از سطح زمین به بالا پرتاب میشود و پس از ۴ ثانیه به سطح زمین برمیگردد. برای حل این سوال ابتدا باید جهتی را به عنوان جهت مثبت انتخاب کنیم. جهت بالا را به صورت قراردادی جهت مثبت قرار میدهیم. از آنجا که از مقاومت هوا صرفنظر کردیم، تنها نیروی وارد شده به توپ، نیروی وزن آن به سمت پایین است. همچنین، شتاب حرکت توپ برابر شتاب جاذبه زمین، یعنی ، است. توپ با سرعت از سطح زمین جدا میشود. جهت u به سمت بالا و مقدار آن مثبت خواهد بود. اما جهت شتاب به سمت پایین و منفی است.
از آنجا که جهت سرعت و شتاب مخالف یکدیگر هستند، سرعت توپ کاهش مییابد و پس از رسیدن به ارتفاع مشخصی صفر میشود. در ادامه، توپ به دلیل نیروی وزن به سمت پایین حرکت میکند. هنگام پایین آمدن، سرعت و شتاب در یک جهت قرار دارند، بنابراین سرعت در جهت منفی افزایش مییابد. بر طبق صورت سوال، مدت زمان کل حرکت توپ برابر ۴ ثانیه است. از آنجا که از مقاومت هوا صرف نظر کردیم، زمان بالا رفتن و پایین آمدن توپ با یکدیگر و برابر ۲ ثانیه است.
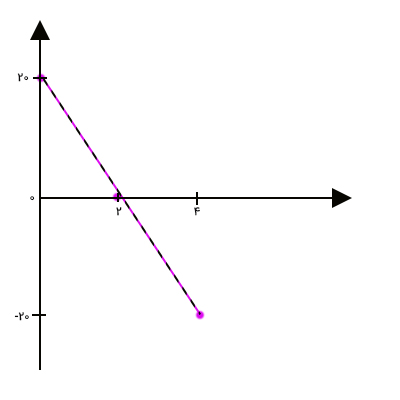
در حرکت با شتاب ثابت، سرعت برحسب زمان به صورت زیر تغییر میکند.
در این مثال، برابر و منفی و برابر و مثبت است.
با توجه به آنکه سرعت نهایی برابر صفر و زمان حرکت توپ به سمت بالا برابر ۲ ثانیه است، سرعت اولیه یا برابر است با:
بنابراین، نمودار سرعت زمان در حرکت توپ به سمت بالا خطی با شیب منفی برابر است که از نقطههای و میگذرد. توپ پس از رسیدن به ارتفاع بیشینه به سمت زمین حرکت میکند و پس از ۲ ثانیه به زمین برخورد میکند. برای بهدست آوردن سرعت برخورد توپ به زمین میتوانیم از دو روش استفاده کنیم:
- استفاده از رابطه
- استفاده از پایستگی انرژی
در اینجا، از پایستگی انرژی استفاده میکنیم. انرژی به دلیل عدم وجود نیروی اتلافی پایسته باقی میماند، بنابراین سرعت توپ هنگام پرتاب از سطح زمین با سرعت برخورد آن به سطح زمین با یکدیگر برابر هستند. از اینرو، توپ با سرعت ۲۰ متر بر ثانیه به زمین برخورد میکند. به این نکته توجه داشته باشید که جهت سرعت توپ هنگام سقوط به سمت پایین و منفی است. در نتیجه، نمودار سرعت زمان در حرکت توپ به سمت پایین خطی با شیب منفی و برابر است که از نقطههای و میگذرد.
سوال ۷
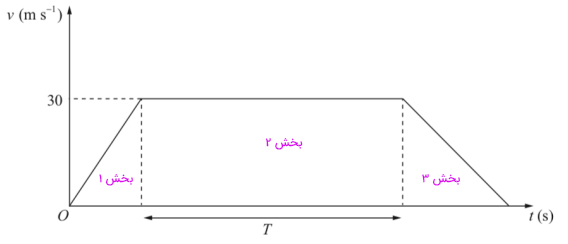
قطار P روی خط مستقیم بین دو ایستگاه به فاصله ۱/۵ کیلومتر از یکدیگر حرکت میکند. نمودار سرعت زمان این قطار در ادامه رسم شده است. قطار P از ایستگاه اول از حالت سکون و با شتاب ثابت شروع به حرکت میکند و پس از ۳۰۰ متر سرعت آن به ۳۰ متر بر ثانیه میرسد. سپس، با این سرعت در مدت زمان T حرکت و راننده قطار در نزدیکی ایستگاه دوم ترمز میکند. قطار با شتاب ثابت ۱/۲۵ متر بر مجذور ثانیه به ایستگاه دوم میرسد و به طور کامل متوقف میشود.
۱) شتاب قطار P را در ۳۰۰ متر اول حرکت آن بهدست آورید.
۲) مقدار T را بهدست آورید.
قطار دومی به نام قطار Q فاصله بین دو ایستگاه را در زمان برابری طی میکند. این قطار از ایستگاه اول از حالت سکون و با شتاب ثابت شروع به حرکت میکند و پس از رسیدن سرعت آن به متر بر ثانیه، بلافاصله راننده با شتاب ثابتی ترمز میکند و پس از مدتی قطار در ایستگاه دوم متوقف میشود.
۳) نمودار سرعت زمان قطار Q را در دستگاه مختصات یکسانی با قطار P رسم کنید.
۴) مقدار را بهدست آورید.

پاسخ
در قسمت اول میخواهیم شتاب قطار را در ۳۰۰ متر ابتدای مسیر بهدست آوریم. بر طبق صورت سوال، سرعت قطار P پس از طی ۳۰۰ متر برابر ۳۰ متر بر ثانیه میشود. سرعت اولیه، سرعت نهایی و جابجایی قطار را داریم، بنابراین برای محاسبه شتاب باید از معادله مستقل از زمان در حرکت روی خط راست استفاده کنیم:
سرعت اولیه قطار P برابر صفر، سرعت نهایی آن برابر ۳۰ متر بر ثانیه و جابجایی برابر ۳۰۰ متر است. با قرار دادن این مقادیر در رابطه فوق، شتاب حرکت را بهدست میآوریم:
در قسمت دوم T را بهدست میآوریم. برای یافتن T باید از مسافت کل طی شده توسط قطار، مسافت طی شده توسط قطار در هر بخش و سطح زیر نمودار سرعت زمان استفاده کنیم. مسافت کل طی شده توسط قطار برابر ۱۵۰۰ متر و بنابراین، مساحت زیر نمودار نیز برابر ۱۵۰۰ است. برای محاسبه مساحت زیر نمودار، آن را به سه بخش تقسیم میکنیم:
- بخش ۱: بر طبق صورت سوال، سرعت قطار پس از طی مسافت ۳۰۰ متر به ۳۰ متر بر ثانیه میرسد. بنابراین، مساحت زیر نمودار در بخش یک برابر ۳۰۰ است.
- بخش ۲: این بخش برابر مساحت مستطیلی به عرض ۳۰ و طول T است.
- بخش ۳: در این قسمت از حرکت، سرعت قطار با شتاب ثابت ۱/۲۵ متر بر مجذور ثانیه کاهش مییابد و پس از گذشت مدت زمان مشخصی به صفر میرسد. بنابراین، برای بهدست آوردن سطح زیر نمودار در بخش ۳، تنها کافی است مسافت طی شده توسط قطار را بهدست آوریم.
در نتیجه، مساحت زیر منحنی در بخش ۳ برابر ۳۶۰ است.
جمع مساحتهای سه بخش برابر ۱۵۰۰ میشود:
در قسمت سوم سوال باید نمودار سرعت زمان برای قطار Q را رسم کنیم. به این نکته توجه داشته باشید که این قطار در دو مرحله حرکت میکند. ابتدا، با شتاب ثابت سرعت آن از صفر به مقدار میرسد، سپس ترمز میکند و با شتاب ثابتی در ایستگاه دوم متوقف میشود. برای رسم نمودار سرعت زمان قطار Q فرض کنید این قطار در مدت زمان به سرعت و در مدت زمان سرعت آن از به صفر میرسد. همچنین، به این نکته توجه داشته باشید که زمان حرکت قطار Q برابر زمان حرکت قطار P است. نمودار سرعت زمان قطار Q به صورت رسم شده در تصویر زیر است.
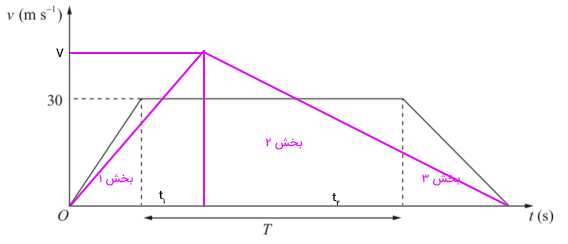
دو قطار مسافت یکسانی را طی میکنند، بنابراین سطح زیر نمودارهای سرعت زمان آنها یکسان است. سطح زیر نمودار قطار Q برابر است با:
همچنین، مجموع زمانهای و برابر زمان حرکت قطار P است. زمان حرکت قطار P را در ادامه بهدست میآوریم.
زمان بین شروع حرکت قطار P تا رسیدن سرعت آن به ۳۰ متر بر ثانیه
قطار از حالت سکون شروع به حرکت میکند و سرعت آن با شتاب ثابت و مثبت ۱/۵ متر بر مجذور ثانیه افزایش مییابد و به ۳۰ متر بر ثانیه میرسد.
زمان حرکت قطار P با سرعت ثابت
قطار به مدت ۲۸ ثانیه با سرعت ثابت ۳۰ متر بر ثانیه حرکت میکند.
زمان توقف کامل قطار P
راننده قطار در نزدیکی ایستگاه ترمز میکند و قطار با شتاب کندشونده ۱/۲۵- متر بر مجذور ثانیه ترمز و سرعت آن از ۳۰ متر بر ثانیه به صفر میرسد.
مدت زمان کل حرکت قطار P برابر ۷۲ ثانیه است. بنابراین، مجموع زمانهای و برابر ۷۲ ثانیه خواهد بود. به جای در رابطه ، مقدار ۷۲ را قرار میدهیم. در نتیجه، سرعت برابر ۴۱/۷ متر بر ثانیه بهدست میآید.
سوال ۸
تمرین و آزمون
سوال ۹
تمرین و آزمون
سوال ۱۰
تمرین و آزمون
سوال ۱۱
تمرین و آزمون
سوال ۱۲
تمرین و آزمون
سوال ۱۳
تمرین و آزمون
سوال ۱۴
تمرین و آزمون
جمعبندی
در این مطلب ابتدا نمودار سرعت زمان را تعریف کردیم. این نمودار تغییرات سرعت برحسب زمان را نشان میدهد. با استفاده از شیب این نمودار میتوانیم شتاب حرکت جسم را بهدست آوریم. با توجه به نوع حرکت جسم روی خط راست، نمودار سرعت زمان خطی افقی برای حرکت با سرعت ثابت یا خطی مستقیم با شیب مشخص برای حرکت با شتاب ثابت است. همچنین، مساحت یا سطح زیر این نمودار، جابجایی جسم را به ما نشان میدهد.
آزمون نمودار سرعت زمان
۱. نمودار سرعت-زمان چه کمکی به تحلیل حرکت اجسام میکند؟
تغییرات سرعت را نسبت به زمان نمایش و ویژگیهایی مانند شتاب و جابجایی را قابل تحلیل میکند.
تنها مقدار جابجایی نهایی را پیدا میکند.
فقط نقطه شروع و پایان حرکت را روی محور زمان نمایش میدهد.
تنها نوع مسیر حرکت جسم را نشان میدهد.
عبارت «تغییرات سرعت را نسبت به زمان نمایش و ویژگیهایی مانند شتاب و جابجایی را قابل تحلیل میکند» درست است، زیرا نمودار سرعت-زمان (v-t) امکان مشاهده روند تغییر سرعت در طول زمان را میدهد و همچنین میتوان با استفاده از شیب نمودار شتاب و با مساحت زیر نمودار جابجایی را محاسبه کرد. عبارت «تنها نوع مسیر حرکت جسم را نشان میدهد» درست نیست چون نمودار v-t فقط اطلاعات سرعت و زمان را ارائه میدهد نه شکل مسیر جسم. عبارت «تنها مقدار جابجایی نهایی را پیدا میکند» ناقص است، چون نمودار v-t اطلاعات بیشتری مانند شتاب و تغییرات سرعت نیز به ما میدهد. «فقط نقطه شروع و پایان حرکت را روی محور زمان نمایش میدهد» نادرست است، زیرا نمودار تمام روند تغییر سرعت را نشان میدهد نه صرفا نقاط ابتدایی و انتهایی.
۲. از یک نمودار سرعت-زمان (v-t)، چه اطلاعاتی را میتوان به صورت مستقیم به دست آورد؟
دما بر اساس محور زمان
جرم جسم از مساحت زیر نمودار
حجم جسم با بررسی منحنی
شتاب جسم با استفاده از شیب نمودار
در نمودار سرعت-زمان، با محاسبه شیب خط یا منحنی میتوان مقدار شتاب جسم را مستقیما به دست آورد، چون شیب نمودار v-t به صورت مستقیم با شتاب رابطه دارد. اما «حجم جسم» و «مساحت زیر نمودار» با جرم مرتبط نیستند و حجم و جرم جسم را نمیتوان از این نمودار به دست آورد. همچنین از محور زمان نمیتوان اطلاعاتی درباره دمای جسم استخراج کرد و دما هیچ ارتباطی با نمودار v-t ندارد.
۳. در نمودار سرعت-زمان (v-t)، محور افقی و محور عمودی به ترتیب چه کمیتهایی را نمایش میدهند؟
محور افقی جابجایی و محور عمودی سرعت را نشان میدهد.
محور افقی شتاب و محور عمودی زمان را نشان میدهد.
محور افقی سرعت و محور عمودی زمان را نشان میدهد.
محور افقی زمان و محور عمودی سرعت را نشان میدهد.
در نمودار سرعت-زمان (v-t)، محور افقی برچسب زمان دارد و محور عمودی مقدار سرعت را نمایش میدهد. عبارت «محور افقی زمان و محور عمودی سرعت را نشان میدهد» با آنچه در تعریف و روش رسم نمودارها توضیح داده شده، مطابقت دارد. گزینههای دیگر («محور افقی سرعت و محور عمودی زمان را نشان میدهد»، «محور افقی شتاب و محور عمودی زمان را نشان میدهد» و «محور افقی جابجایی و محور عمودی سرعت را نشان میدهد») اشتباهاند چون ترتیب درست کمیتها را رعایت نمیکنند یا کمیتهای اشتباهی برای محور انتخاب شدهاند.
۴. کدام عبارت انواع اصلی حرکت جسم روی خط راست را طبق نمودار سرعت-زمان مشخص میکند؟
حرکت سقوط آزاد، حرکت مارپیچ، حرکت با مقاومت هوا، حرکت غیرخطی
حرکت یکنواخت دایرهای، حرکت تناوبی، حرکت با شتاب منفی، حرکت موجی
حرکت با جابجایی متناوب، حرکت پرتابهای، حرکت بینظم، حرکت با ضربه
حرکت سکون، حرکت با سرعت ثابت، حرکت با شتاب ثابت، حرکت با شتاب متغیر
تنها عبارت «حرکت سکون، حرکت با سرعت ثابت، حرکت با شتاب ثابت، حرکت با شتاب متغیر» همه انواع اصلی حرکت روی خط راست و ویژگیهای نمودار v-t مربوط به آنها را مطابق فیزیک حرکت خطی بیان میکند. گزینههایی مانند «حرکت یکنواخت دایرهای» و «حرکت موجی» مربوط به حرکتهای غیرخطی یا بیرون از موضوع نمودار سرعت-زمان خط راست هستند. همچنین گزینه «حرکت سقوط آزاد» و نمونههای مشابه یا خاصاند و چهار نوع حرکت کلی روی خط راست را نمیپوشانند. عبارت «حرکت با جابجایی متناوب» و سایر حالات بینظم و پرتابهای نیز به انواع پایه و مرسوم نمودار v-t خط راست اشاره ندارند.
۵. در نمودار سرعت-زمان (v-t)، شیب خط چه مفهوم فیزیکی را نشان میدهد و برای محاسبه آن چه باید کرد؟
شیب خط، میزان جابجایی جسم را نشان میدهد و با تقسیم مساحت زیر نمودار بر زمان محاسبه میشود.
شیب خط، سرعت متوسط را مشخص میکند و با جمع سرعتهای ابتدا و انتهای بازه و تقسیم بر دو محاسبه میشود.
شیب خط، مقدار شتاب جسم را نمایش میدهد و با تقسیم تغییرات سرعت بر تغییرات زمان به دست میآید.
شیب خط، جهت حرکت جسم را نشان میدهد و با مشاهده علامت محور سرعت تعیین میشود.
در نمودار سرعت-زمان، شیب خط بیانگر «مقدار شتاب جسم» است. مقدار شیب با تقسیم تغییرات سرعت بر مقدار تغییرات زمان به دست میآید. عبارت «نمایش شتاب و محاسبه با تغییر سرعت نسبت به زمان» همان چیزی است که از متن آموزشی کاملا پشتیبانی میشود؛ سایر گزینهها مربوط به جابجایی (مساحت زیر نمودار)، سرعت متوسط، یا جهت حرکت هستند که با شیب خط ارتباط مستقیمی ندارند.
۶. در حرکت با سرعت ثابت، نمودار سرعت-زمان چه ویژگی شکلی دارد و علت آن چیست؟
یک خط افقی روی محور سرعت منفی است.
یک خط با شیب صعودی نسبت به محور زمان است.
یک خط افقی موازی با محور زمان است.
یک منحنی با شیب متغیر نسبت به زمان است.
در حرکت با سرعت ثابت، مقدار سرعت در طول زمان تغییر نمیکند، بنابراین نمودار سرعت-زمان به صورت «یک خط افقی موازی با محور زمان» نمایش داده میشود. این خط افقی نشاندهنده ثبات مقدار سرعت است و هیچ شیب یا افزایشی در مقدار سرعت دیده نمیشود. گزینههای «خط با شیب صعودی» و «منحنی با شیب متغیر» اشتباهاند، چون آنها نشانه تغییر سرعت یا شتاب هستند. گزینه «خط افقی روی محور سرعت منفی» فقط زمانی درست است که سرعت ثابت منفی باشد که در سوال به طور عمومی از حرکت با سرعت ثابت سوال شده است.
۷. کدام گزینه بهدرستی تفاوت نمودار سرعت-زمان در حرکت با شتاب ثابت و شتاب متغیر را بیان میکند؟
در شتاب ثابت، نمودار v-t منحنی و در شتاب متغیر خط راست است.
در شتاب ثابت، نمودار v-t خط افقی و در شتاب متغیر خط شیبدار است.
در شتاب ثابت، نمودار v-t همواره زیر محور زمان و در شتاب متغیر بالای آن قرار دارد.
در شتاب ثابت، نمودار v-t خط راست و در شتاب متغیر، نمودار منحنی با شیب تغییرپذیر است.
در حرکت با شتاب ثابت، نمودار سرعت-زمان (v-t) به صورت خط راست است زیرا سرعت با نرخ ثابت تغییر میکند و شیب خط برابر با شتاب است. اما در حرکت با شتاب متغیر، نمودار سرعت-زمان منحنی میشود و شیب آن در هر نقطه تغییر مییابد. «قرار گرفتن نمودار بالای یا زیر محور» نشاندهنده جهت سرعت است و مرتبط با نوع شتاب ثابت یا متغیر نیست. خط افقی فقط نماد سرعت ثابت است، نه شتاب ثابت. به همین دلیل، فقط بیان «خط راست برای شتاب ثابت و منحنی برای شتاب متغیر» صحیح است.
۸. برای محاسبه جابجایی یک جسم در حرکت خطی با استفاده از نمودار سرعت-زمان (v-t)، باید چه کاری انجام داد و این مقدار مرتبط با کدام بخش از نمودار است؟
بزرگترین مقدار سرعت را روی نمودار پیدا میکنند.
مقدار سرعت اولیه و نهایی را با هم جمع میکنند.
مساحت زیر نمودار v-t را تعیین میکنند.
شیب نمودار v-t را محاسبه میکنند.
برای محاسبه جابجایی جسم با استفاده از نمودار سرعت-زمان (v-t)، باید مساحت سطح زیر نمودار بین دو نقطه زمانی مورد نظر را حساب کرد. این مساحت بیانگر مقدار کل جابجایی جسم در آن بازه زمانی است. محاسبه شیب، فقط شتاب را نشان میدهد و پیدا کردن بزرگترین سرعت یا جمع کردن سرعت اولیه و نهایی، جابجایی را به طور مستقیم به دست نمیدهد. فقط مساحت زیر نمودار v-t مستقیما جابجایی جسم را مشخص میکند.
۹. در نمودار سرعت-زمان (v-t) برای حرکتی که شامل چند فاز مانند سرعت ثابت و شتاب های متفاوت باشد، چه نوع خطوط و ویژگیهایی برای هر فاز انتظار میرود؟
تمام فازها فقط با خطوط افقی نمایش داده میشوند و شیب تغییری ندارد.
در هر فاز، نمودار همیشه سهمی شکل و بدون خطوط مستقیم است.
نمودار فقط به شکل خطوط خمیده رسم میشود و هیچ بخش خطی ندارد.
هر فاز با خط افقی یا شیبدار، بسته به ثابت یا متغیر بودن شتاب دیده میشود.
در حرکت ترکیبی، نمودار v-t میتواند شامل بخشهایی با خطوط افقی (برای سرعت ثابت) و بخشهایی با خطوط شیبدار (برای شتاب ثابت یا متغیر) باشد. خط افقی نشانگر یک فاز با سرعت یکنواخت است و خط شیبدار نمایانگر شتاب گرفتن یا کاهش سرعت. بخشهایی با شیب متغیر یا منحنی نیز در حالت شتاب متغیر ظاهر میشود. عبارت «هر فاز با خط افقی یا شیبدار، بسته به ثابت یا متغیر بودن شتاب دیده میشود» تنها گزینهای است که حالتهای مختلف و ویژگی ترکیبی نمودار را به درستی بیان میکند. مواردی مانند «فقط خطوط خمیده» یا «تمام افقی» محدود به شرایط خاصاند و حالت عمومی حرکات ترکیبی را پوشش نمیدهند.
۱۰. اگر بخشی از نمودار سرعت-زمان (v-t) زیر محور زمان قرار گیرد، این موضوع چه مفهومی درباره حالت حرکت جسم دارد؟
منفی بودن جهت حرکت جسم نسبت به محور انتخاب شده
متوقف شدن جسم در آن بازه زمانی
ثابت بودن شتاب جسم
بدون تغییر بودن سرعت جسم
وقتی ناحیهای از نمودار سرعت-زمان زیر محور زمان قرار دارد، نشانه این است که جهت سرعت جسم نسبت به محور انتخابی، منفی شده است. این ویژگی نشان میدهد جسم در آن بازه زمانی برخلاف جهت محور جابجا میشود. گزینههایی مثل «بدون تغییر بودن سرعت جسم» یا «ثابت بودن شتاب جسم» صرفا به مقدار یا ویژگی دیگری اشاره دارند و الزامی به زیر محور بودن ندارند. همچنین، «متوقف شدن جسم» فقط زمانی رخ میدهد که سرعت برابر صفر باشد، نه زمانی که نمودار زیر محور زمان قرار گیرد. بنابراین، ناحیه زیر محور زمان نشاندهنده منفی بودن جهت حرکت جسم است.
۱۱. در نمودار سرعت-زمان (v-t) حرکت سقوط آزاد، چه ویژگی مهمی نسبت به سایر حرکات خطی وجود دارد و علت منفی بودن شیب این نمودار چیست؟
شیب منفی نمودار، بیانگر شتاب ثابت رو به پایین ناشی از جاذبه زمین است.
شیب منفی نمودار، نشاندهنده کاهش سرعت به دلیل مقاومت هوا است.
در صورت سقوط آزاد، نمودار همیشه افقی است و سرعت تغییری نمیکند.
نمودار خطی است اما شیب آن همیشه مثبت باقی میماند، چون سرعت افزایش مییابد.
در حرکت سقوط آزاد، شیب منفی نمودار سرعت-زمان به دلیل جهت شتاب گرانشی زمین رو به پایین است و مقدار این شیب با شتاب ثابت جاذبه (g) تعریف میشود. عبارت «شیب منفی نمودار، بیانگر شتاب ثابت رو به پایین ناشی از جاذبه زمین است» صحیح است زیرا در سقوط آزاد جسم به سمت پایین شتاب میگیرد و سرعت مقدار منفی پیدا میکند. گزینههایی مانند «کاهش سرعت به دلیل مقاومت هوا» نادرستاند، چون در سقوط آزاد ایدهآل فقط گرانش اثر دارد نه مقاومت هوا. همچنین، نمودار حرکت سقوط آزاد خطی با شیب منفی است و افقی یا با شیب مثبت نیست؛ پس دیگر گزینهها با ویژگی واقعی این حرکت مطابقت ندارند.
۱۲. برای پیدا کردن شتاب لحظهای جسم در حرکت با شتاب متغیر از روی نمودار سرعت-زمان (v-t)، بهترین روش کدام است؟
رسم و محاسبه شیب خط مماس بر نمودار
بررسی دورههای ثابت بودن سرعت روی محور افقی
استفاده از مقدار سرعت اولیه جسم
محاسبه مساحت زیر نمودار در زمان دلخواه
برای تعیین شتاب لحظهای هنگام شتاب متغیر، باید شیب خط مماس بر نمودار v-t را در آن لحظه پیدا کرد. رسم این خط و محاسبه شیب آن مقدار دقیق شتاب را نشان میدهد. «محاسبه مساحت زیر نمودار» جابجایی را میدهد و نه شتاب. «استفاده از مقدار سرعت اولیه» فقط اطلاعات نقطه شروع را فراهم میکند و به شتاب لحظهای ارتباطی ندارد. «بررسی دورههای ثابت بودن سرعت» مربوط به تشخیص حرکت یکنواخت یا سکون است و به محاسبه شتاب متغیر کمکی نمیکند.
۱۳. برای محاسبه جابجایی کل از زیر نمودار سرعت-زمان که ترکیبی از مستطیل، مثلث و ذوزنقه است، کدام روش صحیح است؟
تفاوت بین بزرگترین و کوچکترین مساحت را به عنوان جابجایی محاسبه کنیم.
تنها مساحتهای بالای محور زمان را لحاظ کرده و پایین را نادیده بگیریم.
جمع مساحت تمام بخشهای زیر نمودار با توجه به علامت هر بخش
فقط اندازه مساحت ذوزنقهها را حساب کرده و جمع کنیم.
روش درست، جمع کردن مساحت تمام قسمتهای زیر نمودار سرعت-زمان با توجه به مثبت یا منفی بودن هر بخش نسبت به محور زمان است. جابجایی کل به مجموع جبری مساحت اشکال هندسی وابسته است، چه بالای محور زمان (مثبت) چه پایین آن (منفی). در روشهای فقط در نظر گرفتن ذوزنقه یا تنها قسمتهای مثبت، بخشهایی از جابجایی فیزیکی حذف میشود و نتیجه اشتباه خواهد بود. همچنین، محاسبه اختلاف بزرگترین و کوچکترین مساحت مفهومی در جابجایی ندارد و دقت علمی ندارد. بنابراین، جمع جبری همه مساحتها کاملا درست است.
۱۴. برای تشخیص جهت حرکت جسم و توقف لحظهای آن از نمودار سرعت-زمان (v-t)، کدام روش درست است؟
مقایسه مقدار شتاب در هر بازه زمانی
بررسی علامت سرعت و نقطه عبور نمودار از محور زمان
محاسبه سطح زیر نمودار تا محور زمان
اندازهگیری فاصله نقاط مجاور روی نمودار
برای تعیین جهت حرکت جسم در نمودار سرعت-زمان، باید به علامت سرعت توجه کرد؛ اگر نمودار بالای محور زمان باشد، جهت حرکت مثبت است و اگر پایین محور باشد، جهت حرکت منفی است. توقف لحظهای زمانی رخ میدهد که نمودار از محور زمان (سرعت صفر) عبور کند یا با آن تماس پیدا کند. محاسبه سطح زیر نمودار فقط جابجایی را میدهد، نه جهت یا وضعیت توقف. مقدار شتاب و مقایسه آن، تغییر سرعت را نشان میدهد ولی توقف یا جهت را تعیین نمیکند. فاصله نقاط مجاور روی نمودار فقط برای سنجش تغییرات سرعت کاربرد دارد و نشانهای از جهت یا توقف نیست.
۱۵. در مورد نمودار سرعت-زمان (v-t) برای چترباز، تاثیر مقاومت هوا در هر مرحله سقوط چگونه دیده میشود؟
سرعت ابتدا سریع رشد کرده، سپس به آرامی کاهش مییابد و سرانجام پس از باز شدن چتر به شدت کم میشود.
ابتدا سرعت خطی افزایش مییابد و سپس با خط افقی ثابت میماند.
سرعت در تمام مراحل بدون تغییر میماند تا چتر باز شود و ناگهان صفر شود.
سرعت همیشه با شیب منفی کاهش مییابد تا به صفر برسد.
نمودار سرعت زمان چترباز نشان میدهد که در آغاز حرکت، سرعت با شیب زیاد افزایش پیدا میکند، اما با افزایش مقاومت هوا، شیب نمودار کم شده و سرعت به تدریج به مقدار ثابتی نزدیک میشود (سرعت حد). پس از باز شدن چتر، مقاومت هوا به شدت زیاد شده و سرعت ناگهانی افت میکند. بنابراین، «سرعت ابتدا سریع رشد کرده، سپس به آرامی کاهش مییابد و سرانجام پس از باز شدن چتر به شدت کم میشود» توصیف دقیقی از وضعیت نمودار در مراحل مختلف است.
۱۶. اگر شیب نمودار سرعت-زمان (v-t) در یک بازه زمانی افزایش پیدا کند، کدام حالت درباره شتاب جسم درست است؟
شتاب جسم در آن بازه زمانی افزایش یافته است.
سرعت متوسط جسم در آن بازه کاهش یافته است.
شتاب جسم منفی و ثابت باقی میماند.
مساحت زیر نمودار با زمان کاهش مییابد.
وقتی شیب نمودار سرعت-زمان در یک بازه افزایش یابد، یعنی مقدار شتاب جسم رو به افزایش است، چون شیب این نمودار برابر با شتاب است و هرچه شیب بیشتر شود، شتاب هم بزرگتر میشود. «شتاب جسم در آن بازه زمانی افزایش یافته است» توصیف درستی از این وضعیت است. اما «سرعت متوسط جسم در آن بازه کاهش یافته» با افزایش شیب الزاما برقرار نیست و اطلاعات کافی درباره جهت تغییرات سرعت نمیدهد. همچنین «شتاب جسم منفی و ثابت باقی میماند» نادرست است، چون ثابت و منفی بودن شباهتی به تغییر شیب ندارد. «مساحت زیر نمودار با زمان کاهش مییابد» نیز به جابجایی مربوط میشود و به افزایش شیب یا شتاب اشاره نمیکند.
۱۷. اگر نمودار سرعت-زمان یک جسم خط افقی و موازی محور زمان باشد، کدام نوع حرکت را نشان میدهد؟
جسم با شتاب ثابت حرکت میکند.
جسم با شتاب متغیر حرکت میکند.
جسم با سرعت ثابت حرکت میکند.
جسم در سکون کامل قرار دارد.
وقتی در نمودار سرعت-زمان یک خط افقی دیده شود، یعنی مقدار سرعت در طول زمان تغییر نمیکند و مقدار آن ثابت است. این وضعیت نشاندهنده حرکت جسم با سرعت ثابت است. در حالت سکون، نمودار روی محور سرعت صفر قرار میگیرد اما همچنان افقی است که فقط حالت خاصی از سرعت ثابت است. حرکت با شتاب ثابت با خط شیبدار و حرکت با شتاب متغیر با منحنی یا خط خمیده مشخص میشود، بنابراین چنین خط افقیای به طور مستقیم نشاندهنده حرکت با سرعت ثابت است و سایر حالات با خطوط شیبدار یا منحنی نمایش داده میشوند.
۱۸. اگر نمودار سرعت-زمان (v-t) دو جسم دارای شیبهای متفاوت باشد، تفاوت کلیدی آنها درباره مقدار شتاب چیست؟
جسم با شیب بیشتر دارای شتاب بزرگتری است.
شیب نمودار v-t فقط نوع حرکت را نشان میدهد نه مقدار شتاب را.
هر دو جسم با هر شیب شتاب یکسان دارند.
جسم با شیب کمتر دارای شتاب بیشتری است.
در نمودار سرعت-زمان (v-t)، شیب خط نشاندهنده مقدار شتاب است. هرچه شیب نمودار بزرگتر باشد، مقدار شتاب جسم نیز بیشتر خواهد بود؛ بنابراین «جسم با شیب بیشتر دارای شتاب بزرگتری است» درست است. گزینه «شیب کمتر دارای شتاب بیشتری است» نادرست است، چون افزایش شیب مستقیما نشاندهنده افزایش شتاب است. گزینه «شیب فقط نوع حرکت را نشان میدهد نه مقدار شتاب» صحیح نیست زیرا مقدار شتاب مستقیما از شیب تعیین میشود. همچنین، شیبهای متفاوت هرگز شتاب یکسان را ایجاد نمیکنند، پس گزینه «هر دو جسم شتاب یکسان دارند» هم غلط است.













بسیار مفید و کاربردی