انواع تابع در ریاضی – به زبان ساده + حل مثال
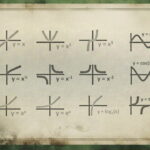
توابع، از مهمترین مفاهیم مورد استفاده در ریاضی هستند که در بسیاری از حوزههای فنی نظیر مهندسی نیز مورد استفاده قرار میگیرند. توابع ریاضی، انواع بسیار گستردهای دارند. از انواع تابع در ریاضی میتوان به تابع یک به یک، تابع چند به یک، تابع پوشا، تابع غیرپوشا، تابع ثابت، تابع صعودی، تابع نزولی، تابع همانی، تابع چندجملهای، تابع صفر، تابع خطی، تابع درجه دو، تابع درجه سه، تابع قدر مطلق، تابع گویا، تابع علامت، تابع زوج، تابع فرد، تابع متناوب، تابع وارون، تابع جز صحیح، تابع مرکب، تابع نمایی، تابع جبری، تابع توانی، تابع مثلثاتی، تابع لگاریتمی و غیره اشاره کرد. در این مقاله، قصد داریم به معرفی تمام این توابع به همراه نمایش نمودار آنها و حل چند مثال بپردازیم.
- میآموزید تابع را با تعریف دقیق و ریاضی بیان کنید.
- یاد میگیرید دامنه، برد و همدامنه یک تابع را تشخیص دهید.
- خواهید آموخت ویژگی و تفاوتهای انواع تابع مانند یک به یک، پوشا و ثابت را بررسی کنید.
- نحوه استفاده از مشتق برای تعیین صعودی یا نزولی بودن توابع را یاد میگیرید.
- با طبقهبندی توابع بر اساس فرم معادله مانند همانی، خطی، درجه دو و سه آشنا میشوید.
- تشخیص انواع توابع جبری، توانی، مثلثاتی و لگاریتمی را میآموزید.
تابع چیست ؟
«تابع» (Function)، یک عبارت، قاعده یا قانون است که رابطه بین یک متغیر مستقل و یک متغیر وابسته را نمایش میدهد. به عبارت دیگر، رابطه بین مجموعهای از مقادیر ورودی و مجموعهای از مقادیر خروجی، توسط تابع تعریف میشود. علامت تابع در ریاضی، حرف f است.

تابع زیر را در نظر بگیرید:
x، متغیر مستقل و معرف مقادیر ورودی تابع است. با قرار دادن هر یک از مقادیر x، مقادیر خروجی f(x) به دست میآیند. به عنوان مثال، برای ، داریم:
بنابراین:
به مجموعههای بالا، دامنه و برد نیز میگویند. تابع در ریاضی، انواع بسیار زیادی دارد. به عنوان مثال، تابعی که در اینجا مثال زدیم، یک تابع جبری، یکجملهای، توانی، درجه دو، زوج و صعودی است. در ادامه، شما را با انواع تقسیمبندیهای توابع ریاضی و فرم کلی آنها آشنا خواهیم کرد.
برد، دامنه و هم دامنه تابع چیست ؟
برد، دامنه و هم دامنه، از مهمترین مفاهیم مورد نیاز برای آشنایی با انواع تابع در ریاضی هستند. هر یک از این مفاهیم به صورت زیر تعریف میشوند:
- «دامنه» (Domain): مجموعه تمام مقادیر ورودی تابع است.
- «همدامنه» (Codomain): مجموعه تمام مقادیر خروجی احتمالی تابع است.
- «برد» (Range): مجموعه تمام مقادیر خروجی به دست آمده از ورودیهای تابع است.
انواع تابع در ریاضی چه هستند ؟
تقسیمبندیهای مختلفی برای توابع ریاضی وجود دارد. از مهمترین انواع تابع بر اساس معیارهای مختلف میتوان به موارد زیر اشاره کرد:
- انواع تابع بر اساس رابطه بین دامنه و برد: تابع یک به یک، تابع چند به یک، تابع پوشا، تابع یک به یک و پوشا، تابع غیرپوشا و تابع ثابت
- انواع تابع بر اساس فرم معادله: تابع همانی، تابع خطی، تابع درجه دو یا مربعی، تابع درجه سه یا مکعبی و تابع چندجملهای
- انواع تابع بر اساس برد: تابع قدر مطلق، تابع گویا، تابع علامت، تابع فرد، تابع زوج، تابع متناوب یا دورهای، تابع جز صحیح، تابع وارون و تابع مرکب
- انواع تابع بر اساس دامنه: تابع جبری، تابع مثلثاتی و تابع لگاریتمی
در بخشهای بعدی این مقاله، تمام موارد ذکر شده را به طور کامل معرفی و بررسی میکنیم.
انواع تابع بر اساس رابطه بین دامنه و برد
یکی از معیارهای مهم برای تقسیمبندی انواع تابع در ریاضی، تعداد روابط بین اعضای موجود در دامنه و برد است. بر این اساس، توابع ریاضی به انواع تابع یک به یک، تابع چند به یک، تابع پوشا، تابع یک به یک و پوشا، تابع غیرپوشا و تابع ثابت تقسیم میشوند.
تابع یک به یک چیست ؟
«تابع یک به یک» (One-to-One Function یا Injective Function)، یکی از انواع خاص تابع در ریاضی است که در آن، هر مولفه برد، تنها با یک مولفه دامنه رابطه دارد. به زبان سادهتر، در تابع یک به یک، خروجیها تکرار نمیشوند. اگر تابعی مانند f(x)، یک به یک باشد، شرط زیر در آن برقرار است:
و
دو مجموعه A و B را در نظر بگیرید که در آن، B تابعی از A است.
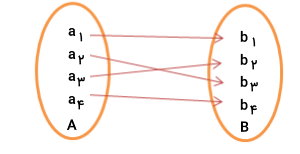
میگوییم ، یک تابع یک به یک است؛ اگر برای هر عضو A، یک عضو مخصوص در B وجود داشته باشد. دو تابع زیر را در بگیرید:
f(x)، یک تابع یک به یک است؛ چراکه برای ورودیهای متفاوت، خروجیهای متفاوت را تولید میکند. در طرف مقابل، g(x)، یک تابع یک به یک نیست؛ زیرا برای برخی از ورودیها، خروجیهای یکسان تولید میکند. به عنوان مثال، با محاسبه مقدار g(x) در و ، داریم:
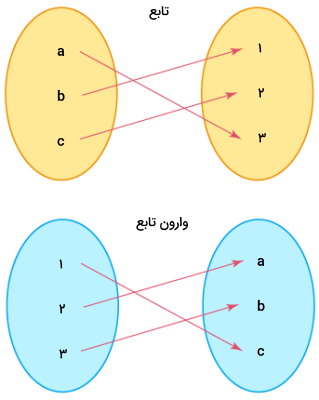
بنابراین، g(x) نمیتواند یک به یک باشد. تصویر زیر، یک به یک بودن یا نبودن توابع f(x) و g(x) را با نمایش رابطه بین مولفههای برد و دامنه نمایش میدهد.
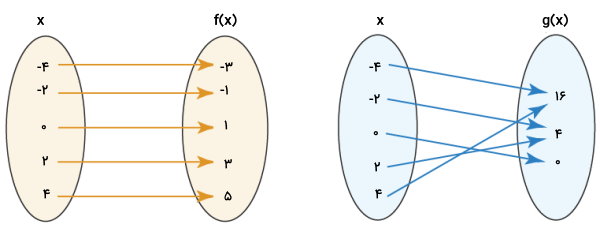
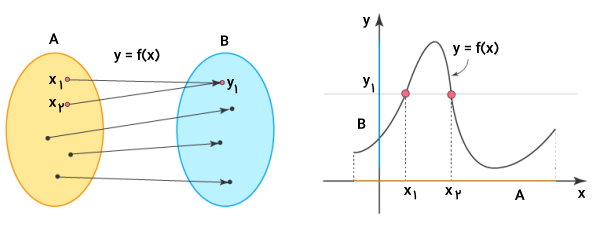
همانطور که مشاهده میکنید، به هیچ یک از مولفههای f(x)، بیشتر از یک فلش وصل نمیشود. در طرف مقابل، مولفههایی در g(x) وجود دارند که دو فلش به آنها وصل میشود. بنابراین، f(x)، یک به یک بوده و g(x)، یک به یک نیست. یکی از روشهای بررسی یک به یک بودن انواع تابع در ریاضی، اجرای آزمون خط افقی بر روی نمودار است. به عنوان مثال، نمودارهای توابع f(x) و g(x) را در نظر بگیرید.
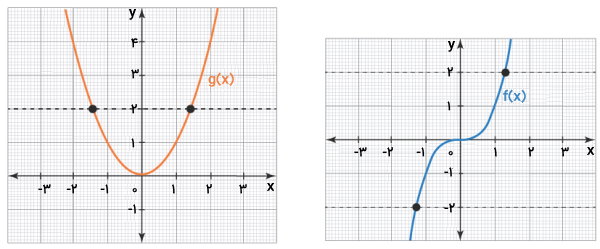
با رسم خط افقی دلخواه بر روی نمودار f(x)، این خط، تنها در یک نقطه نمودار را قطع میکند. از اینرو، f(x) به عنوان یک تابع یک به یک در نظر گرفته میشود. در طرف دیگر، در نمودار تابع g(x)، میتوانیم یک خط افقی را رسم کنیم که نمودار را در بیش از یک نقطه قطع میکند. در نتیجه، g(x)، یک به یک نیست.
روشهای مختلفی برای تشخیص یک به یک بودن توابع وجود دارد. در صورت تمایل به یادگیری این روشها، مطالعه مطلب «تابع یک به یک و پوشا — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» را به شما پیشنهاد میکنیم.
خواص تابع یک به یک چه هستند ؟
برخی از مهمترین خواص توابع یک به یک عبارت هستند از:
- اگر دو تابع f(x) و g(x) یک به یک باشند، ترکیب آنها () نیز یک به یک خواهد بود.
- اگر تابع f(x) یک به یک باشد، دامنه f(x) با برد f'(x) و دامنه f'(x) با برد f(x) برابر خواهد بود.
- اگر یک تابع یک به یک باشد، نمودار آن صعودی یا نزولی (یکنوا) خواهد بود.
- اگر تابع f(x) یک به یک باشد، برای هر x موجود در دامنه، روابط و برقرار خواهند بود.
- اگر یک به یک باشد، تابع g(x) قطعا یک به یک خواهد بود.
- اگر تابع f(x) یک به یک باشد، نمودار f(x) و f'(x) نسبت به خط دارای تقارن محوری خواهند بود.
مثال ۱: اثبات یک به یک بودن تابع
با استفاده رویکرد جبری، ثابت کنید که تابع ، یک به یک است.
تابع f(x)، یک به یک است؛ اگر و تنها اگر بتوانیم از به برسیم. به این منظور ، ابتدا و را مینویسیم:
اکنون و را برابر با یکدیگر قرار میدهیم:
عبارتهای مساوی را از دو طرف رابطه حذف میکنیم:
ضرایب دو طرف را با هم ساده میکنیم:
از دو طرف رابطه ریشه سوم میگیریم:
در نتیجه، f(x)، یک تابع یک به یک است.
تابع چند به یک چیست ؟
به تابعی که یک به یک نباشد، «تابع چند به یک» (Many-to-One Function) میگویند. در این نوع از توابع ریاضی، دو یا چند مولفه موجود در مجموعه دامنه با یکی از المانهای موجود در برد ارتباط دارند. به زبان سادهتر، توابع چند به یک میتوانند خروجیهای تکراری داشته باشند.
تصویر زیر، مفهوم تابع چند به یک را توسط نمودار ون نمایش میدهد.
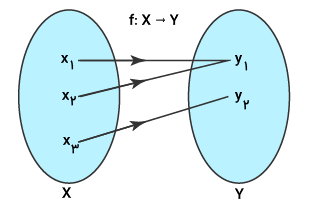
اگر y تابعی از x بوده () و دو یا چند مولفه دامنه f (متلق به مجموعه x) به یکی از مولفههای برد f (متعلق به مجموعه y) ارتباط داشته باشد، f(x) به عنوان یک تابع چند به یک در نظر گرفته میشود. به عنوان مثال، مجموعههای A و B را به ترتیب به عنوان دامنه و برد تابع f در نظر بگیرید:
همانطور که مشاهده میکنید، در سه جفت اول تابع f، با وجود تغییر دامنه یا ورودی (۱، ۲ و ۳)، برد یا خروجی (x) تکرار میشود. بنابراین، f، یک تابع چند به یک است. تابع چند به یک، انواع مختلفی دارد. از معروفترین انواع تابع چند به یک در ریاضی میتوان به تابع ثابت و تابع پوشا اشاره کرد.
خواص تابع چند به یک چه هستند ؟
برخی از مهمترین ویژگیهای توابع چند به یک عبارت هستند از:
- دامنه تابع چند به یک، حداقل دو مولفه با برد یکسان دارد.
- تعداد مولفههای موجود در دامنه تابع چند به یک، بیشتر از مولفههای برد آن است.
- در صورت وجود یک مولفه در برد تابع چند به یک، به آن تابع ثابت میگویند.
مثال ۲: تعیین تابع چند به یک
زوج مرتبهای زیر را در نظر بگیرید:
کدامیک از زوجمرتبهای بالا، تابع چند به یک است؟
حل مثال را از f شروع میکنیم. در این مجموعه، سه ورودی مختلف، یک جواب مشترک دارند (). به علاوه، هیچ دو خروجی متفاوتی را نمیتوان یافت که ورودی مشترک داشته باشند. بنابراین، f، یک تابع چند به یک است.

در مجموعه g، تمام خروجیها، یک ورودی مشترک دارند. از اینرو، این مجموعه زوجمرتب، بیانگر یک تابع نیست. در مجموعه h، تمام ورودیها، با یک خروجی ثابت جفت میشوند. علاوه بر این، هیچیک از خروجیها، دارای ورودی مشترک نیستند. به همین دلیل، h نیز در گروه توابع چند به یک قرار میگیرد. البته h، یک تابع ثابت نیز محسوب میشود. در بخشهای بعدی به معرفی این نوع تابع خواهیم پرداخت.
در نهایت، به سراغ زوجمرتبهای مجموعه i میرویم. در این مجموعه، تمام ورودیها، با یک خروجی متمایز جفت میشوند. در نتیجه، این مجموعه، یک تابع یک به یک بوده و چند به یک نیست.
تابع پوشا چیست ؟
«تابع پوشا» (Onto Function یا Surjective Function)، یکی از انواع تابع چند به یک است که در آن، تمام مولفههای موجود در برد، با مولفهها موجود در دامنه رابطه دارند. مجموعه دامنه A و مجموعه برد B را در نظر بگیرید. این دو مجموعه، از طریق تابع f به یکدیگر ارتباط دارند.
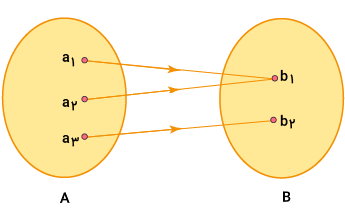
به ، یک تابع پوشا میگویند؛ اگر به ازای هر عضو از مجموعه B (به ازای هر )، حداقل یک عضو در مجموعه A (یک ) وجود داشته و باشد. به عنوان مثال، برای مجموعهها و تابع نمایش داده شده در تصویر بالا، داریم:
همانطور که مشاهده میکنید، تمام مولفههای موجود در برد، در حداقل یک جفت از تابع حضور دارند. بنابراین، f، یک تابع پوشا است.
خواص تابع پوشا چه هستند ؟
مهمترین مشخصات توابع پوشا عبارت هستند از:
- در تابع پوشا، هر یک از مولفههای موجود در برد به حداقل یک مولفه در دامنه وصل میشود.
- تمام توابع پوشا، یک وارون راست دارند.
- هر تابع دارای وارون راست را میتوان به عنوان یک تابع پوشا در نظر گرفت.
تابع یک به یک و پوشا چیست ؟
به تابعی که مشخصات تابع یک به یک و تابع پوشا را داشته باشد، «تابع یک به یک و پوشا» (Onto and One-to-One Function) یا «تابع دوسویی» (Bijective Function) میگویند. تصویر زیر، مفهوم تابع دوسویی را نمایش میدهد.

بر اساس تصویر بالا، هر یک از مولفههای مجموعه سمت راست، تنها به یک مولفه از مجموعه سمت چپ وصل میشوند. بنابراین، رابطه بین این مجموعهها را میتوان به عنوان یک تابع یک به یک در نظر گرفت. علاوه بر این، تمام مولفههای مجموعه سمت راست، حداقل با یک مولفه از مجموعه سمت چپ رابطه دارند. از اینرو، تابع معرف رابطه آنها، پوشا نیز هست.
تابع غیر پوشا چیست ؟
«تابع غیرپوشا» (Into Function)، تابعی است که در آن، هر یک از مولفههای مجموعه دامنه، تنها به یکی از مولفههای مجموعه برد وصل میشوند و حداقل یک مولفه از مجموعه برد، به هیچ مولفهای از مجموعه دامنه وصل نمیشود. به عنوان مثال، مجموعههای زیر را در نظر بگیرد.
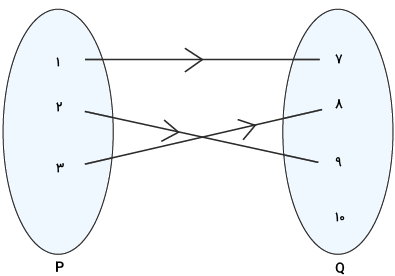
مولفههای مجموعه سمت راست، تابعی از مولفههای مجموعه سمت چپ هستند. بنابراین میتوانیم مجموعه راست (Q) را به عنوان دامنه و مجموعه سمت چپ (P) را به عنوان همدامنه در نظر میگیریم. این مجموعهها و تابع آنها به صورت زیر نوشته میشوند:
همانطور که مشاهده میکنید، تمام اعضای مجموعه P با تنها یکی از اعضای مجموعه Q رابطه دارند. به علاوه، حداقل یکی از اعضای Q (عدد ۱۰)، به هیچ یک از اعضای P وصل نمیشود. در نتیجه، f، یک تابع غیرپوشا است.
مثال ۳: تعیین پوشا یا غیرپوشا بودن تابع
تصویر زیر، رابطه بین دو مجموعه X و Y را نمایش میدهد.
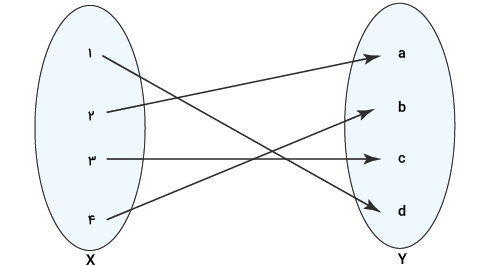
آیا ، یک تابع غیرپوشا است؟
در تابع بالا، مولفههای دامنه و برد عبارت هستند از:
تابع یا همان رابطه بین دامنه و برد، به صورت زیر نوشته میشود:
همانطور که مشاهده میکنید، تمام مولفههای دامنه با یکی از مولفههای برد رابطه دارند. به علاوه، هیچ مولفهای از برد، بدون رابطه نیست. بنابراین، تابع ، یک تابع پوشا بوده و غیرپوشا نیست.
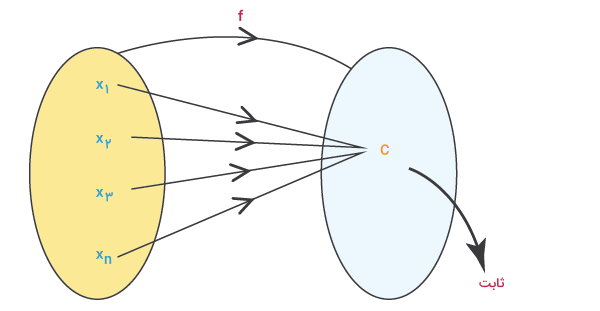
تابع ثابت چیست ؟
«تابع ثابت» (Constant Function)، یکی از انواع خاص تابع در ریاضی است که در آن، برد تابع دارای یک مولفه ثابت است. به زبانسادهتر، در تابع ثابت، ورودی بر روی خروجی تاثیر نمیگذارد.
از نظر ظاهری، نمودار تابع ثابت به شکل یک خط راست افقی و موازی با محور x در محورهای مختصات است. دامنه این نوع از انواع تابع در ریاضی، مقادیر محور x را دربرمیگیرد و برد آن، تنها با یکی از مقادیر محور y برابری میکند. تصویر زیر، نمودار یک تابع ثابت () را نمایش میدهد.
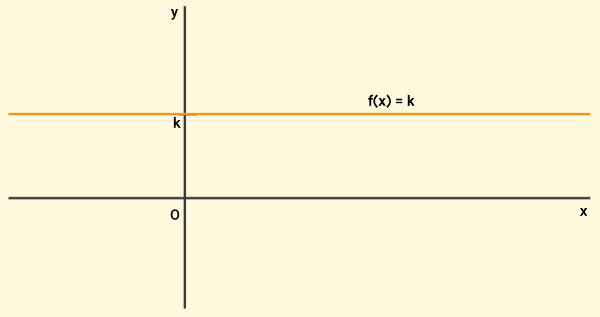
هر تابعی که فرم آن به صورت یا باشد، به عنوان یک تابع ثابت در نظر گرفته میشود. k، یک عدد حقیقی و ثابت است. علاوه بر این، f(x) یا y، هیچ وابستگی به x ندارد. در ادامه، چند مثال از تابع ثابت را آوردهایم:
تابع ثابت، یکی از انواع تابع خطی در ریاضی به شمار میرود. فرم کلی توابع خطی به صورت زیر نوشته میشود:
m و k، ثابتهای عددی هستند. فرم بالا را با فرم تابع ثابت مقایسه کنید:
با مقایسه این فرمها، میتوان نتیجه گرفت که در تابع ثابت، m برابر با صفر است:
m، شیب منحنی تابع خطی را نمایش میدهد. با توجه به این موضوع، شیب منحنی تابع ثابت برابر با صفر خواهد بود.
توابع ثابت، ویژگیهای منحصر به فرد متعددی دارند. در صورت تمایل به آشنایی با این ویژگیها، مطالعه مطلب «تابع ثابت و خصوصیات آن | به زبان ساده» را به شما پیشنهاد میکنیم.
مثال ۴: تعیین برد تابع ثابت
تابع یک تابع ثابت است. خروجی این تابع برای برابر با ۲ میشود. برد تابع را به دست بیاورید.
با توجه به اطلاعات مسئله، داریم:
در توابع ثابت، خروجی (k)، به ورودی (x) بستگی ندارد. بنابراین:
به این ترتیب:
فارغ از مقدار ورودی، خروجی f(x) همواره برابر با ۲ میشود. برد تابع ثابت ، برابر با k است. در نتیجه، برد تابع f(x)، مجموعه تک عضوی {۲} است.
تابع صعودی و تابع نزولی چیست ؟
«تابع صعودی» (Increasing Function) و «نزولی» (Decreasing Function)، توابعی هستند که با افزایش مقدار ورودی، مقدار خروجی آنها افزایش یا کاهش مییابد. اگر با افزایش ورودی x، خروجی f(x) افزایش پیدا کند، f(x) به عنوان یک تابع صعودی در نظر گرفته میشود. اگر با افزایش ورودی x، خروجی f(x) کاهش پیدا کند، f(x) به عنوان یک تابع نزولی در نظر گرفته میشود. تصویر زیر، چند نمونه از توابع صعودی و نزولی را نمایش میدهد.
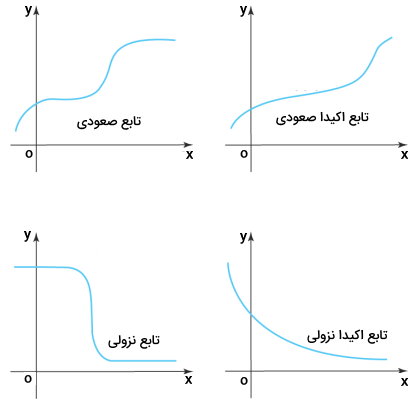
یکی از روشهای تشخیص صعودی یا نزولی بودن توابع، تعیین علامت مشتق آنها است. اگر مشتق یک تابع بزرگتر یا مساوی ۰ باشد، به آن تابع، صعودی میگویند. اگر مشتق تابع کوچکتر یا مساوی ۰ باشد، به آن تابع، نزولی گفته میشود. به عنوان مثال، تابع را در نظر بگیرید. مشتق این تابع برابر است با:
مقدار x هر چه که باشد، حاصل عبارت بالا دارای علامت مثبت خواهد بود. بنابراین، ، یک تابع صعودی است. توابع صعودی و نزولی، با عنوان «تابع یکنوا» (Monotone Function) نیز شناخته میشوند.
انواع تابع بر اساس فرم معادله
یکی دیگر از معیارهای مهم برای تقسیمبندی انواع تابع در ریاضی، فرم معادله معرف تابع است. بر این اساس میتوان توابع ریاضی را به انواع تابع همانی، تابع خطی، تابع درجه دو یا مربعی، تابع درجه سه یا مکعبی و تابع چندجملهای تقسیم کرد.
تابع همانی چیست ؟
«تابع همانی» (Identity Function)، یکی انواع جالب تابع در ریاضی است که مقدار ورودی را به عنوان خروجی بازمیگرداند. به عبارت دیگر، در تابع همانی، ورودی و خروجی با هم برابر هستند.
دو مجموعه A و B را در نظر بگیرید. اگر B تابعی از A باشد () و با قرار دادن هر یک از مولفههای B (مانند ) در f، به همان مولفه برسیم ()، میگوییم f، یک تابع همانی است. توابع همانی، معمولا با حرف I (ابتدای عبارت Identity) نشان داده میشوند. تصویر زیر، نمونهای از رابطه بین دامنه و برد در یک تابع همانی را نمایش میدهد.
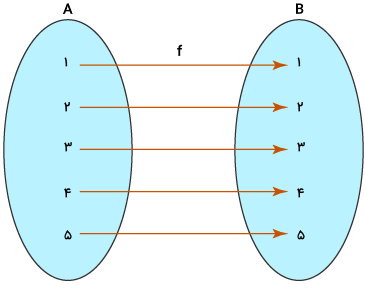
مجموعههای تابع بالا عبارت هستند از:
به عبارت دیگر، B با A برابر است. بنابراین، تابع f به صورت زیر نمایش داده میشود:
نمودار تابع همانی در تصویر زیر آورده شد است.
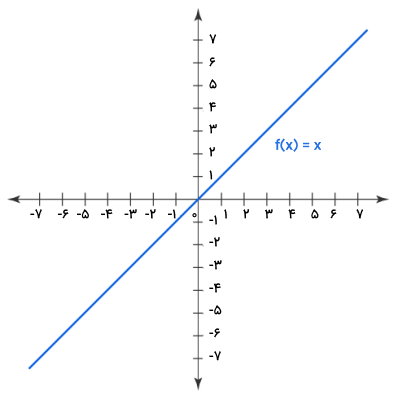
خواص تابع همانی چه هستند ؟
مهمترین خواص تابع همانی عبارت هستند از:
- تابع همانی، یک تابع خطی با مقادیر حقیقی است.
- شیب نمودار تابع همانی نسبت به محورهای x و y برابر با ۴۵ درجه است.
- تابع همانی یکی از انواع توابع دوسویی (یک به یک و پوشا) محسوب میشود.
- تابع همانی و وارون آن، با یکدیگر برابر بوده و دارای نمودار یکسان هستند.
- تابع همانی است؛ اگر باشد.
مثال ۵: بررسی همانی بودن تابع
تابع را در نظر بگیرید. ثابت کنید f(f(x))، یک تابع همانی است.
رابطه f(f(x))، با قرار دادن تابع f(x) در خودش به دست میآید:
بر اساس خواص تابع همانی، f(f(x)) یک تابع همانی در نظر گرفته میشود.
تابع چند جمله ای چیست ؟
«تابع چندجملهای» (Polynomial Function)، از شناخته شدهترین، مهمترین و پرکاربردترین انواع تابع در ریاضی است که مطابق با فرم زیر نوشته میشود:
همانطور که مشاهده میکنید، توابع چندجملهای، از کنار هم قرار گرفتن عبارتهای جبری به وجود میآیند.
تصویر زیر، اجزای مختلف فرم استاندارد تابع چندجملهای را نمایش میدهد.
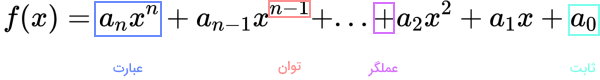
در توابع چندجملهای، توجه به نکات زیر ضروری است:
- ، ثابتهای عددی و حقیقی هستند.
- ، با عنوان ضریب پیشرو شناخته میشود.
- در یک تابع چندجملهای، نمیتواند برابر با صفر باشد.
- ، یک عدد صحیح غیرمنفی است.
- تمام توانها در تابع چندجملهای باید یک عدد صحیح باشند.
توابع زیر، چند نمونه از انواع تابع چندجملهای در ریاضی هستند:
به خاطر داشته باشید که ضرایب ثابت در توابع جملهای میتوانند کسری، منفی، مثبت یا حتی صفر باشند. با این وجود، در صورت غیرصحیح بودن تابع، نمیتوان آن را در گروه چندجملهایها قرار داد. به عنوان مثال، توابع زیر در گروه توابع چندجملهای قرار نمیگیرند:
توان یکی از xها در تابع اول، برابر با و توان y در تابع دوم برابر با ۳- است. بنابراین، این دو تابع به عنوان توابع چندجملهای در نظر گرفته نمیشوند.

انواع تابع چند جمله ای
روشهای مختلفی برای تقسیمبندی انواع تابع چندجملهای وجود دارد. بر اساس تعداد عبارتهای جبری، این توابع به انواع زیر تقسیم میشوند:
- «یکجملهایها» (Monominals): تابع چندجملهای متشکل از یک عبارت جبری مانند
- «دوجملهایها» (Binominals): تابع چندجملهای متشکل از دو عبارت جبری مانند
- «سهجملهایها» (Trinomials): تابع چندجملهای متشکل از سه عبارت جبری مانند
- و غیره
درجه یک تابع چندجملهای، بزرگترین توان متغیرهای ورودی آن (معمولا x) را نمایش میدهد. انواع توابع چندجملهای بر اساس درجه عبارت هستند از:
- تابع صفر
- تابع خطی یا درجه یک
- تابع مربعی یا درجه دو
- تابع مکعبی یا درجه سه
- و غیره
به دلیل اهمیت توابع بالا، در بخشهای مجزا به معرفی هر یک از آنها میپردازیم.
مثال ۶: تعیین صفرهای تابع چندجمله ای
صفرهای تابع ، در کجا رخ میدهند؟
برای به دست آوردن موقعیت صفرهای یک تابع (محل تقاطع نمودار تابع با محور y دستگاه مختصات)، فرمول آن را برابر با صفر قرار میدهیم:
بنابراین، در ، مقدار تابع برابر با صفر میشود.
تابع صفر چیست ؟
«تابع ثابت» (Zero Function)، یکی از انواع توابع ثابت است که در گروه توابع چندجملهای نیز قرار میگیرد. فرم کلی تابع صفر به صورت زیر نوشته میشود:
دقیقا مانند تمام توابع ثابت، مقدار خروجی تابع صفر نیز به مقدار ورودی (x) بستگی ندارد. طبق تعریف ریاضی، ورودی تابع صفر باید عضو مجموعه اعداد حقیقی باشد. بنابراین، برد این تابع عبارت است از:
به علاوه، دامنه تابع صفر، یک مجموعه تکعضوی () است. تصویر زیر، نمودار تابع صفر را نمایش میدهد.
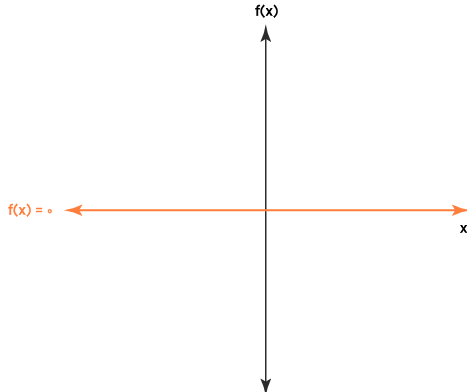
مشابه دیگر توابع ثابت، نمودار تابع ، یک خط راست افقی (دارای شیب صفر) و موازی با محور x است. به طور دقیقتر، این تابع، معادله محور x در دستگاه مختصات دوبعدی را نشان میدهد. اغلب خواص تابع صفر به خواص تابع ثابت شباهت دارند. با این وجود، تابع صفر، تنها تابعی است که هم در گروه توابع فرد و هم در گروه توابع زوج قرار میگیرد. در بخشهای بعدی، به معرفی توابع زوج و فرد خواهیم پرداخت.
تابع خطی چیست ؟
«تابع خطی» (Linear Function)، یکی از سادهترین و پرکاربردترین انواع تابع در ریاضی است. این تابع، در گروه توابع چندجملهای با درجه ۱ قرار دارد. فرم کلی توابع خطی به صورت زیر نوشته میشود.
x، متغیر تابع و a و b، ثابتهای عددی هستند. تصویر، نمودار سه تابع خطی را نمایش میدهد.
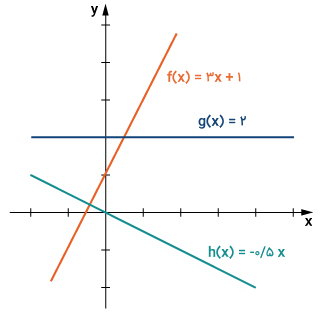
توابع خطی بالا عبارت هستند از:
ثابتهای عددی a و b میتوانند دارای مقادیر مثبت، منفی و حتی صفر باشند. نمودار توابع خطی، از قواعد زیر پیروی میکند:
- اگر باشد، با افزایش x (حرکت از تا )، نمودار تابع خطی به سمت بالا میل میکند (تابع خطی، صعودی خواهد بود).
- اگر باشد، با افزایش x (حرکت از تا )، نمودار تابع خطی به سمت پایین میل میکند (تابع خطی، نزولی خواهد بود).
- اگر باشد، با افزایش یا کاهش x (حرکت از تا یا برعکس)، نمودار تابع خطی تغییر نمیکند (تابع خطی، افقی خواهد بود).
در تصویر بالا، یک نمونه از قواعد بالا نمایش داده شده است.
مفهوم شیب در توابع خطی و فرم های مختلف این توابع
نمودار تمام توابع خطی به صورت یک خط راست نمایش داده میشود. از اینرو، به فرم کلی این نوع تابع در ریاضی، معادله خط نیز میگویند. یکی از مشخصههای اصلی هر خط، شیب آن است. در یک تابع خطی، شیب، به صورت تغییر مقدار خروجی y، به ازای تغییر یک واحدی ورودی x تعریف میشود. این مفهوم، تندی و جهتگیری خط را به طور همزمان نمایش میدهد. اگر شیب تابع خطی، مثبت باشد، با افزایش x، مقدار y نیز افزایش مییابد. در طرف مقابل، اگر شیب تابع خطی، منفی باشد، با افزایش x، مقدار y کاهش مییابد. در صورت ۰ بودن شیب، تغییر x، تاثیری بر روی مقدار y نخواهد داشت (y، یک خط افقی با ارتفاع ثابت خواهد بود).
اکنون، معادله یک تابع خطی را در نظر بگیرید:
ضریب متغیر x در معادله بالا (ضریب ثابت a)، شیب تابع خطی را نمایش میدهد. از دیگر اطلاعات قابل استخراج از این معادله میتوان به محل برخورد نمودار تابع خطی با محور y اشاره کرد. یک تابع خطی، محور y را در مختصات قطع میکند. در منابع ریاضی، شیب با حرف انگلیسی «m» نشان داده میشود. بر این اساس، فرم متداول معادله تابع خطی برای نمایش شیب آن، به صورت زیر است:
به این فرم از معادله، «فرم شیب-تقاطع» (Slope-Intercept Form) میگویند. در برخی از موارد، نحوه نمایش معادله تابع خطی با فرمهای معرفی شده تفاوت دارد. به عنوان مثال، در صورت عبور یک تابع خطی از نقطه با شیب m، معادله تابع در رابطه زیر صدق میکند:
یا
در این شرایط، معادله تابع خطی مطابق با فرم زیر نوشته میشود:
یا
به این معادله، «معادله شیب خط بین دو نقطه» یا «معادله نقطه-شیب» (Point-Slope Equation) میگویند. تمام خطوط غیرعمودی، با استفاده از تابع خطی قابل تعریف هستند. از اینرو، میتوان مختصات نقاط روی خطوط غیرعمودی را با استفاده از معادله شیب-تقاطع یا نقطه-شیب به دست آورد. با این وجود، امکان تعریف خطوط عمودی با استفاده معادلات مذکور وجود ندارد. معادله خطوط عمودی، توسط معادله نمایش داده میشوند. با توجه به توضیحات قبل، یک فرم استاندارد به منظور تعریف معادله خط مورد استفاده قرار میگیرد. این فرم عبارت است از:
a و b در معادله بالا، نمیتوانند صفر باشند.
خواص تابع خطی چه هستند ؟
ویژگیهای توابع خطی عبارت هستند از:
- فرم توابع خطی با معادله خط یکسان () است.
- اگر شیب برابر با ۰ باشد، تابع خطی به تابع ثابت (خط افقی) تبدیل میشود.
- برد و دامنه تابع خطی، در مجموعه اعداد حقیقی قرار دارند.
- تابع خطی، یک به یک است.
- اگر شیب دو تابع خطی برابر باشد، این دو تابع، موازی یکدیگر هستند.
- اگر حاصلضرب شیبهای دو تابع خطی برابر با ۱- باشد، این دو تابع، بر هم عمود هستند.
- خط عمودی، یک تابع خطی نیست.
- توابع خطی، در نمایش تابع هدف در مسائل برنامهریزی خطی کاربرد دارند.
مثال ۷: به دست آوردن رابطه تابع خطی با استفاده از مختصات دو نقطه
خطی را در نظر بگیرید که از نقاط و عبور میکند. معادله تابع معرف این خط را به دست بیاورید.
فرم استاندارد تابع خطی به صورت زیر نوشته میشود:
m، شیب تابع را نمایش میدهد. اگر مختصات دو نقطه از خط را داشته باشیم، میتوانیم شیب آن خط را با استفاده از رابطه زیر به دست بیاوریم:
نقاط داده شده در صورت مسئله را به صورت زیر مینویسیم:
به این ترتیب، داریم:
با قرار دادن مختصات یکی از نقاط خط در رابطه زیر، معادله خط را به دست میآوریم:
به عبارت دیگر:
این معادله، معادله تابع خطی گذرنده از دو نقطه و است.

تابع مربعی یا تابع درجه دو چیست ؟
«تابع مربعی» (Quadratic Function)، یک تابع چندجملهای و جبری با یک یا چند متغیر درجه ۲ است. مطابق با تعریف، تابع مربعی، حداقل یک عبارت با توان ۲ دارد. به همین دلیل، این تابع معمولا با عنوان «تابع درجه دو» (Second Degree Function) نیز شناخته میشود.
فرم استاندارد تابع درجه دو، عبارت است از:
برای اینکه یک تابع، به عنوان تابع چندجملهای درجه دو در نظر گرفته شود، مقدار a نباید برابر با صفر باشد (شرط برقرار باشد). توابع زیر، مثالهایی از تابع درجه دو هستند:
در تمام توابع بالا، بیشترین توان متغیر تابع برابر با ۲ بوده و شرط برقرار است. بنابراین، این توابع در گروه چندجملهای درجه دو یا مربعی قرار میگیرند. نمودار توابع مربعی، معمولا شبیه به ∪ یا ∩ است. تصویر زیر، شکل کلی توابع مربعی را نمایش میدهد.
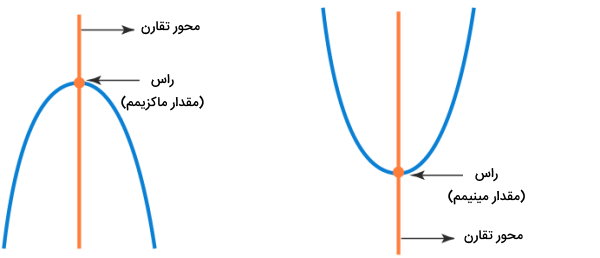
اگر ضریب a، دارای مقدار مثبت باشد، شکل نمودار تابع درجه به صورت ∩ بوده و اگر این ضریب منفی باشد، شکل نمودار به صورت ∪ خواهد بود. اجزای اصلی نمودار تابع مربعی، عبارت هستند از:
- محور تقارن
- راس (مقدار حداقلی یا حداکثری تابع)
دامنه توابع درجه دو در مجموعه اعداد حقیقی قرار میگیرد. برد این توابع، به ضریب متغیر درجه دو (a) بستگی دارد. بر این اساس، داریم:
- اگر باشد، بازه برد برابر با خواهد بود.
- اگر باشد، بازه برد برابر با خواهد بود.
محاسبه موقعیت راس تابع درجه دو
برای محاسبه موقعیت راس تابع درجه دو، از مفهوم مشتق استفاده میکنیم. مشتق یک تابع، شیب خط مماس بر نمودار آن را در یک نقطه دلخواه نمایش میدهد. خط مماس بر نمودار توابع درجه دو در محل قرارگیری راس، یک خط افقی با شیب صفر است. بنابراین، اگر مشتق تابع درجه دو را برابر با صفر قرار دهیم، میتوانیم مقدار x راس را به دست بیاوریم. مختصات راس نمودار تابع را در نظر بگیرید:
پس از تعیین مشتق تابع، برابر قرار دادن آن با صفر () و حل تابع بر اساس x، مقدار به دست میآید. این مقدار را درون تابع اصلی قرار میدهیم تا به برسیم. به این ترتیب، مختصات k را به دست میآوریم. اگر ضریب a، دارای مقدار مثبت باشد، مینیمم تابع در قرار دارد. در صورت منفی بودن ضریب a، ماکزیمم تابع در قرار خواهد داشت.
حل معادلات تابع درجه دو و پیدا کردن صفرهای این تابع، از اهمیت بسیار زیادی در مسائل ریاضی برخوردار است. فرمول حل معادله درجه دو به صورت زیر نوشته میشود:
با استفاده از این فرمول، دو مقدار برای x به دست میآید. این مقادیر، طول نقاط برخورد نمودار تابع درجه دو با محور y (موقعیتهای ) را نمایش میدهند.
مثال ۸: یافتن مختصات نقاط تقاطع نمودار با محور y
محل تقاطع نمودار تابع با محور y را تعیین کنید.
تابع f(x)، یک تابع چندجملهای درجه دو است. محل تقاطع نمودار این نوع تابع با محور y، از رابطه زیر به دست میآید:
با توجه فرمول f(x)، داریم:
این مقادیر را در فرمول بالا قرار میدهیم:
به این ترتیب، در ، مقدار تابع برابر با صفر میشود. در این نقاط، نمودار تابع با محور y دستگاه مختصات برخورد میکند.

تابع مکعبی یا تابع درجه سه چیست ؟
آخر تابعی که در این بخش به آن میپردازیم، تابع درجه سه یا «تابع مکعبی» (Cubic Function) است. توابع مکعبی، نوعی از توابع چندجملهای و جبری با حداکثر توان ۳ هستند.
فرم استاندارد معادله یک تابع مکعبی یا درجه سه به صورت زیر نوشته میشود:
تمام ضرایب ثابت در تابع بالا، میتوانند عضوی از مجموعه اعداد حقیقی باشند. به علاوه، ضریب a، نمیتواند برابر با صفر باشد. به دلیل فرد بودن بزرگترین توان متغیر x در تابع درجه سه، این تابع، حداقل یک ریشه حقیقی دارد. توابع زیر، دو مثال از تابع مکعبی هستند:
تصویر زیر، نمودار این دو تابع را نمایش میدهد.
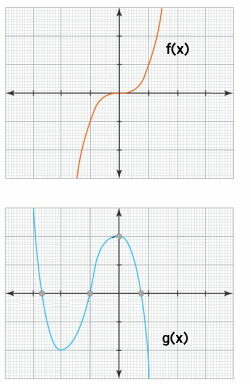
دامنه و برد توابع معکبی، در مجموعه اعداد حقیقی قرار میگیرند. نمودار این توابع، چند نقطه مهم دارند. به نقاطی که بعد از آنها، شیب نمودار تغییر میکند، «نقاط بحرانی» (Critical Point) و به نقطهای که بعد از آن، تقعر/تحدب نمودار به تحدب/تقعر تغییر میکند، «نقطه عطف» (Inflection Point) میگویند. طول نقاط بحرانی، با استفاده از روابط زیر به دست میآید:
یا
اگر عبارت زیر رادیکال، مثبت باشد، تابع مکعبی دارای دو نقطه بحرانی خواهد بود. در صورت ۰ شدن عبارت زیر رادیکال، تابع فقط دارای یک نقطه بحرانی است. اگر عبارت زیر رادیکال منفی باشد، هیچ نقطه بحرانی وجود ندارد. برای به دست آوردن مختصات نقطه عطف تابع درجه سه، کافی است مشتق مرتبه دوم آن را برابر با صفر قرار دهیم (). به این ترتیب، مختصات نقطه عطف برابر با میشود.
انواع تابع بر اساس برد
برد یک تابع، مجموعهای از تمام خروجیهای به دست آمده برای ورودیهای مختلف آن تابع است. انواع تابع در ریاضی بر اساس برد به تابع قدر مطلق، تابع گویا، تابع علامت، تابع فرد، تابع زوج، تابع متناوب یا دورهای، تابع جز صحیح، تابع وارون و تابع مرکب تقسیم میشوند. در ادامه، به معرفی اجمالی هر یک از این توابع میپردازیم.
تابع قدر مطلق چیست ؟
«تابع قدر مطلق» (Modulus Function یا Absolute Value Function)، تابعی است که علامت خروجی آن، به مثبت یا منفی بودن ورودی بستگی ندارد. خروجی تابع قدر مطلق، همیشه غیرمنفی (۰ یا مثبت) است.
فرم کلی توابع قدر مطلق به صورت زیر نوشته میشود:
یا
دامنه و برد توابع قدر مطلق، به ترتیب عبارت هستند از:
به عبارت دیگر، دامنه یک تابع قدر مطلق، در مجموعه اعداد حقیقی قرار دارد. در طرف دیگر، برد یک تابع قدر مطلق، فقط مقادیر غیرمنفی مجموعه اعداد حقیقی (صفر تا بینهایت) را در برمیگیرد.

فرمول و نمودار تابع قدر
در توابع قدر مطلق، مقدار خروجی، به مقدار ورودی بستگی دارد. با این وجود، علامت خروجی، همواره غیر منفی است. به عنوان مثال، تابع زیر را در نظر بگیرید:
اگر علامت ورودی x مثبت یا مقدار x برابر با ۰ باشد، f(x) برابر با x خواهد بود. در صورت منفی بودن x، مقدار f(x) برابر با x- میشود. این شروط به صورت زیر نوشته میشوند:
به طور کلی، داریم:
تصویر زیر، نمودار تابع قدر مطلق بالا را نمایش میدهد. همانطور که مشاهده میکنید، این نمودار، در ربع اول و دوم (نیمه بالایی و مثبت محور y) قرار دارد.
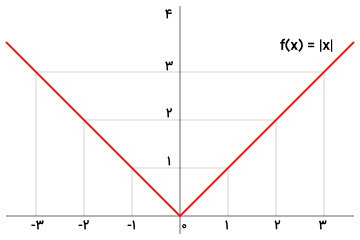
خواص تابع قدر مطلق چه هستند ؟
تابع قدر مطلق، یکی از انواع تابع در ریاضی با خواص منحصر به فرد است. برخی از این خواص عبارت هستند از:
- تابع قدر مطلق، همواره غیرمنفی است. بنابراین، هیچ ورودی نمیتواند خروجی این تابع را منفی کند.
- نامساوی تابع قدر مطلق
- برای ، جوابی وجود ندارد.
- برای تمام مقادیر حقیقی f(x)، شرط برقرار است.
- عملیاتهای جبری تابع قدر مطلق
- (به شرطی که y برابر با ۰ نباشد.)
تابع گویا چیست ؟
«تابع گویا» (Rational Function)، یکی از انواع تابع در ریاضی است که به صورت تقسیم چندجملهایها نوشته میشود. به عبارت دیگر، صورت و مخرج یک تابع گویا، چندجملهای هستند. البته به شرطی که مخرج برابر با صفر نباشد.
فرم کلی توابع گویا به صورت زیر نوشته میشود:
به عنوان مثال، تمام توابع زیر، در گروه توابع گویا قرار میگیرند:
به خاطر داشته باشید که فقط صورت توابع گویا میتواند برابر با یک عدد ثابت باشد. اگر مخرج یک کسر با صورت چندجملهای برابر با عدد ثابت باشد، نمیتوان آن را به عنوان تابع گویا در نظر گرفت. به عنوان مثال، کسر زیر، یک تابع گویا نیست:
مخرج هیچ کسری نمیتواند برابر با صفر باشد. این نکته، از اهمیت بالایی در تعیین دامنه و برد توابع گویا برخوردار است. دامنه یک تابع گویا، مجموعهای از تمام مقادیر قابل استفاده به عنوان x را در برمیگیرد. به عنوان مثال، برای به دست آوردن دامنه ، ابتدا مخرج کسر را برابر ۰ قرار میدهیم و آن را بر حسب x حل میکنیم. دامنه تابع، مجموعه تمام اعداد حقیقی، به غیر از عددی است که در آن، مخرج کسر برابر با ۰ شده است.
برای تعیین برد تابع گویا، y را جایگزین f(x) کرده و معادله را بر حسب x بازنویسی میکنیم. اکنون، مخرج کسر را برابر با ۰ قرار میدهیم. برد تابع گویا، تمام مقدار حقیقی، به غیر از عددی است که در آن، مخرج کسر برابر با ۰ شده است. در ادامه، نحوه به دست آوردن دامنه و برد تابع گویا را با حل یک مثال توضیح میدهیم.

مثال ۹: تعیین برد و دامنه تابع گویا
برد و دامنه را به دست بیاورید.
برای به دست آوردن دامنه تابع مورد سوال، مخرج آن () را برابر با ۰ قرار میدهیم:
سپس، رابطه بالا را برای تعیین x حل میکنیم:
بنابراین، دامنه f(x) برابر است با:
برای تعیین برد f(x)، تغییر متغیر زیر را انجام میدهیم:
اکنون، معادله بالا را بر حسب x بازنویسی میکنیم:
در مرحله بعد، مخرج کسر بالا را برابر با ۰ در نظر میگیریم:
به این ترتیب، برد f(x) برابر است با:
تابع علامت چیست ؟
«تابع علامت» (Signum Function)، تابعی است که به منظور نمایش علامت تابع برای مقادیر مختلف ورودی مورد استفاده قرار میگیرد. بنابراین، خروجی تابع علامت میتواند مثبت، منفی یا صفر باشد.
فرم کلی تابع علامت به صورت زیر نوشته میشود:
تصویر زیر، نمودار تابع علامت را نمایش میدهد.
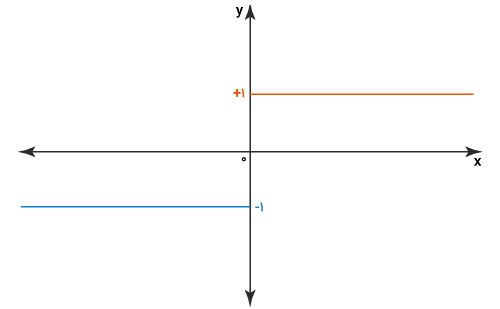
دامنه و برد تابع علامت، عبارت هستند از:
به عبارت دیگر، دامنه تابع علامت (مقادیر ورودی x) در مجموعه اعداد حقیقی قرار دارد. در طرف دیگر، برد این نوع تابع، در بازه بسته ۱+ تا ۱- است. تابع علامت یکی از انواع تابع فرد و پلهای در ریاضی است. در بخشهای بعدی، به معرفی توابع فرد و پلهای نیز خواهیم پرداخت.
مثال ۱۰: تعیین خروجی تابع علامت
خروجی تابع زیر را برای مقادیر را به دست بیاورید.
تابع بالا، یک تابع علامت را نمایش میدهد. مقدار خروجی این تابع برای ورودیهای مثبت، ۱+ بوده و برای ورودیهای منفی، ۱- است. در صورت صفر بودن مقدار ورودی نیز خروجی این تابع برابر با ۰ میشود. به این ترتیب، داریم:
توابع زوج و فرد چه هستند ؟
«توابع زوج و فرد» (Even and Odd Functions)، یکی دیگر از تقسیمبندیهای کلی انواع تابع در ریاضی است که به علامت ورودی و خروجی بستگی دارد. اگر با قرار دادن مقادیر منفی x در تابع، علامت تابع تغییر نکند، میگوییم تابع ما زوج است. اگر با قرار دادن مقادیر منفی x در تابع، علامت تابع تغییر کند، میگوییم تابع ما فرد است.
فرم کلی توابع زوج به صورت زیر نوشته میشود:
به عنوان مثال، تابع را در نظر بگیرید. اگر به جای x در تابع، x- را قرار دهیم، خواهیم داشت:
به همین ترتیب میتوانیم نتیجه بگیریم که توابع x۶ ،x۴ و x۸ نیز زوج هستند. البته روج بودن توان عبارتهای یک تابع، به معنای زوج بودن آن تابع نیست. به عنوان مثال، در تابع ، با قرار دادن x- به جای x، شرط برقرار نمیشود. تصویر زیر، شکل کلی نمودار توابع زوج را نمایش میدهد.
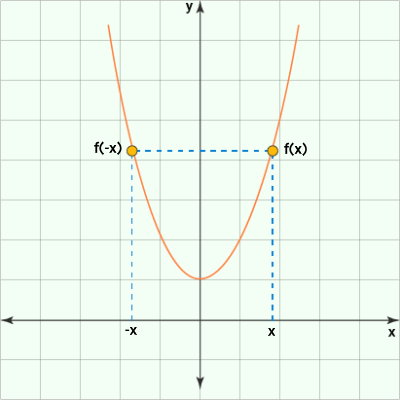
فرم کلی توابع فرد نیز به صورت زیر نوشته میشود:
به عنوان مثال، تابع را در نظر بگیرید. اگر به جای x در تابع، x- را قرار دهیم، خواهیم داشت:
به این ترتیب، تابع و توابعی مانند x۵ ،x۳ و x۷، توابع فرد در نظر گرفته میشوند. تصویر زیر، شکل کلی نمودار توابع زوج را نمایش میدهد.
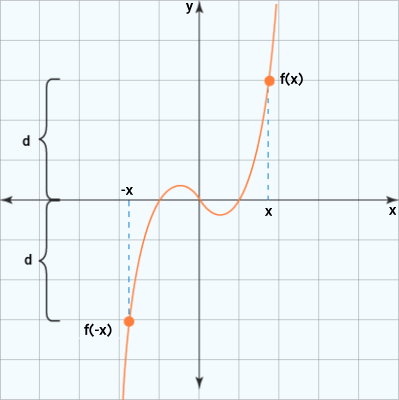
تابع صفر ()، یک تابع زوج و فرد محسوب میشود. علاوه بر توابع زوج و فرد، گروه دیگری از توابع وجود دارند که در هیچکدام از این دو تقسیمبندی قرار نمیگیرند. به عنوان مثال، تابع زیر را در نظر بگیرید:
با قرار دادن x- به جای x، خواهیم داشت:
برای این تابع، داریم:
به عبارت دیگر، هیچکدام از شرطهای زوج یا فرد بودن تابع در f(x) برقرار نیست. بنابراین، f(x)، یک «تابع نه زوج نه فرد» است.
خواص تابع زوج و فرد چه هستند ؟
از مهمترین ویژگیهای توابع زوج و فرد میتوان به موارد زیر اشاره کرد:
- جمع دو تابع زوج، یک تابع زوج بوده و جمع دو تابع فرد، یک تابع فرد است.
- تفاضل دو تابع زوج، یک تابع زوج بوده و تفاضل دو تابع فرد، یک تابع فرد است.
- جمع یک تابع زوج با یک تابع فرد، نه زوج نه فرد است؛ مگر اینکه یکی از توابع، صفر باشد.
- ضرب دو تابع زوج، یک تابع زوج بوده و ضرب دو تابع فرد نیز یک تابع زوج است.
- تقسیم دو تابع فرد بر یکدیگر، یک تابع زوج بوده و تقسیم دو تابع زوج بر یکدیگر نیز یک تابع زوج است.
- تقسیم یک تابع زوج بر یک تابع فرد، یک تابع فرد است.
- ترکیب دو تابع زوج، یک تابع زوج بوده و ترکیب دو تابع فرد، یک تابع فرد است.
- ترکی یک تابع زوج با یک تابع فرد، یک تابع زوج است.
تابع متناوب چیست ؟
«تابع متناوب» (Periodic Function)، تابعی است که در بازههای منظم، خودش را تکرار میکند. فرم کلی این نوع از انواع تابع در ریاضی به صورت زیر نوشته میشود:
در رابطه بالا، P، دوره تناوب تابع متناوب است. تصویر زیر، نمودار چند تابع متناوب را نمایش میدهد. دامنه توابع متناوب، تمام عضوهای مجموعه اعداد حقیقی را دربرمیگیرد. برد این توابع نیز در یک بازه ثابت و مشخص قرار دارد.
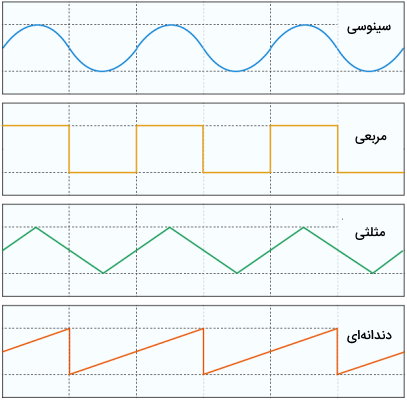
تابع سینوس، یکی از معروفترین توابع متناوب است. این تابع در گروه توابع مثلثاتی نیز قرار میگیرد. دوره تناوب تابع سینوس برابر با است. به عبارت دیگر، اگر به جای x در فرمول این تابع، عبارت را قرار دهیم، هیچ تغییری در خروجی رخ نمیدهد.
فرمول با دوره تناوب ، فرمول ژاکوبی و سری فوریه، از مهمترین توابع متناوب هستند.
خواص تابع متناوب چیست ؟
در ادامه، برخی از مهمترین خواص توابع متناوب را فهرست میکنیم:
- نمودار توابع متناوب، متقارن است. این نمودار، خود را در راستای محور افقی دستگاه مختصات تکرار میکند.
- دور تناوب تابع متناوب، برابر با اندازه بازهای است که تابع خود را در آن تکرار میکند.
- اگر ، تابع متناوب با دوره تناوب P باشد، نیز تابعی متناوب با همان دوره تناوب (P) خواهد بود.
- اگر ، تابع متناوب با دوره تناوب P باشد، نیز تابعی متناوب با همان دوره تناوب (P) خواهد بود.
- اگر ، تابع متناوب با دوره تناوب P باشد، نیز تابعی متناوب با همان دوره تناوب (P) خواهد بود.
تابع وارون چیست ؟
«تابع وارون» (Inverse Function)، یکی از مهمترین انواع تابع در ریاضی است که عملکرد تابع معمولی را معکوس میکند. در یک تابع، با قرار دادن یک ورودی (مانند x)، به یک خروجی مشخص (مانند y) میرسیم. در وارون تابع، با قرار دادن خروجی تابع معمولی (y)، ورودی آن (x) را به دست میآوریم.
تابع وارون با نمایش داده میشود. تنها زمانی میتوان وارون یک تابع را به دست آورد که آن تابع، یک به یک و پوشا باشد. علامت را با نسبت عکس f (کسر ) اشتباه نگیرید. تصویر زیر، نمودار یک تابع وارونپذیر و تابع وارون آن را نمایش میدهد.
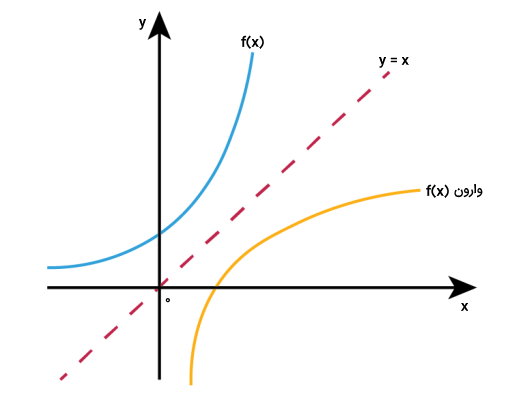
مراحل تعیین وارون یا معکوس تابع
به منظور تعیین معکوس یا وارون یک تابع، مراحل زیر را دنبال کنید:
- تغییر متغیر
- عوض کردن جای x و y در فرمول تابع
- حل فرمول جدید برای به دست آوردن y
- تغییر متغیر
به عنوان مثال، فرم کلی تابع خطی را در نظر بگیرید:
مطابق با دو مرحله اول معکوسسازی تابع، داریم:
بر اساس دو مرحله بعدی، خواهیم داشت:
تابع جز صحیح یا تابع پله ای چیست ؟
«تابع پلهای» (Step Function) یا «تابع بزرگترین جز صحیح» (Greatest Integer Function)، تابعی است که ورودی را گرفته و به کوچکترین عدد صحیح نزدیک به آن تبدیل میکند. این تابع با عناوین دیگری نظیر تابع جز صحیح و تابع براکت نیز شناخته میشود.
فرم کلی توابع جز صحیح عبارت است از:
اگر x، بین اعداد صحیح n و n+۱ قرار داشته باشد، برابر با n خواهد بود.
به عنوان مثال، اگر x برابر با ۵/۱ باشد، براکت آن برابر میشود با:
زیرا
در صورتی که x برابر با ۵/۱- باشد، براکت آن برابر خواهد بود با:
همانطور که مشاهده میکنید، دامنه یک تابع جز صحیح میتواند هر عدد از مجموعه اعداد حقیقی باشد. با این وجود، برد این نوع از انواع تابع در ریاضی، فقط به مجموعه اعداد صحیح محدود میشود. تصویر زیر، نمودار یک تابع جز صحیح را نمایش میدهد.
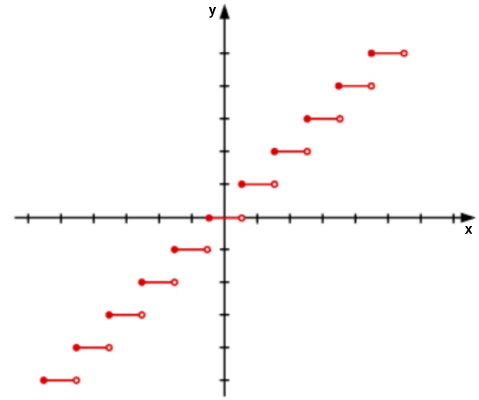
تابع مرکب چیست ؟
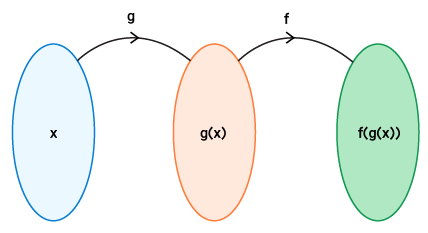
«تابع مرکب» (Composite Function)، تابعی است که از ترکیب دو یا چند تابع به وجود میآید. در این نوع تابع از انواع تابع در ریاضی، خروجی یک تابع به عنوان ورودی تابع دیگر در نظر گرفته میشود. به عنوان مثال، f(x) و g(x) را در نظر بگیرید. تابع مرکب این دو را با یا نمایش میدهیم. در اینجا، g(x) به عنوان ورودی f(x) در نظر گرفته شده است. به همین ترتیب، در تابع مرکب یا ، تابع f(x) به عنوان ورودی g(x) در نظر گرفته میشود. تصویر زیر، مفهوم تابع مرکب را به خوبی نمایش میدهد.
دامنه یک تابع مرکب، به دامنه توابع اولیه آن بستگی دارد. به عنوان مثال، تابع مرکب را در نظر بگیرید. اگر دامنه هر یک از این توابع به صورت زیر باشد:
دامنه ترکیب آنها به صورت زیر خواهد بود:
به عبارت دیگر، دامنه تابع مرکب، همان دامنه تابع داخلی است. در صورت مشخص بودن رابطه جبری توابع، تعیین دامنهها ترکیب آنها طی مراحل زیر صورت میگیرد:
- تعیین دامنه تابع داخلی g(x)
- تعیین دامنه تابع مرکب f(g(x))
- اشتراک دامنههای تابع داخلی و مرکب
نحوه تعیین برد تابع مرکب، تفاوتی با دیگر توابع ندارد. برای آشنایی با این موضوع، به مثال تعیین برد و دامنه تابع گویا مراجعه کرده یا مثال بعدی را مطالعه کنید.
مثال ۱۱: تعیین برد و دامنه تابع مرکب
دو تابع زیر را در نظر بگیرید:
دامنه و برد را به دست بیاورید.
در تابع مرکب مورد سوال، g(x)، تابع داخلی است. با در نظر داشتن این موضوع، دامنه را بر اساس مراحل زیر به دست میآوریم:
- تعیین دامنه تابع داخلی g(x)
- تعیین دامنه تابع مرکب f(g(x))
- اشتراک دامنههای تابع داخلی و مرکب
تابع g(x)، یک تابع گویا با مخرج چندجملهای است. برای تعیین دامنه این تابع، مخرج آن را برابر با صفر قرار میدهیم:
مخرج تابع گویا نمیتواند صفر باشد. بنابراین، دامنه تابع g(x) میتواند تمام عضوهای مجموعه اعداد حقیقی به غیر از عدد ۲- را به عنوان ورودی بگیرد. در مرحله بعدی، g(x) را درون f(x) قرار میدهیم:
مطابق با مرحله دوم، دامنه تابع بالا را به دست میآوریم. این دامنه، تمام عضوهای مجموعه اعداد حقیقی، به غیر از عددی است که مخرج کسر را صفر میکند. به این ترتیب، داریم:
بنابراین، x نمیتواند مقادیر ۳- و را بگیرید. بر اساس مرحله سوم، اگر دامنه g(x) را برابر با A و دامنه f(x) با ورودی g(x) را برابر با B در نظر بگیریم، دامنه f(g(x)) برابر خواهد بود با:
اکنون، نوبت به تعیین برد f(g(x)) میرسد. به این منظور، تابع مرکب f(g(x)) را برابر با y قرار میدهیم و آن را برای به دست آوردن x بازنویسی میکنیم:
مخرج کسر بالا نمیتواند برابر با صفر باشد. اگر این مخرج را برابر با صفر قرار دهیم، خواهیم داشت:

بنابراین، y نمیتواند برابر با باشد. در نتیجه، برد تابع مرکب f(g(x)) عبارت است از:
تابع نمایی چیست ؟
«تابع نمایی» (Exponential Function)، تابعی یکجملهای با توان متغیر است. فرمهای مختلف تابع نمایی به صورت زیر نوشته میشوند:
b، یک عدد ثابت بزرگتر از صفر، به غیر از یک ( و ) است. در ادامه، چند مثال از توابع نمایی میآوریم:
تصویر زیر، نمودار دو تابع نمایی ( و ) را نمایش میدهد.
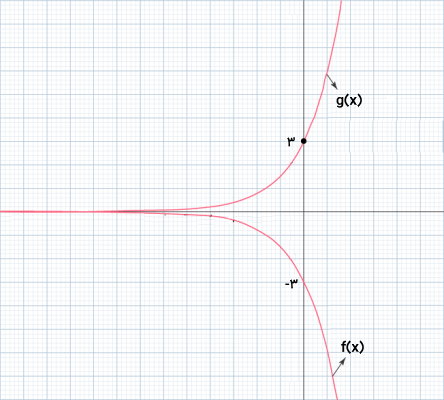
دامنه توابع نمایی، در مجموعه اعداد حقیقی (بازه تا ) قرار میگیرد. همانطور که مشاهده میکنید، بخشی از نمودار تابع نمایی به یک خط افقی میل میکند. مختصات y برای این خط را برابر با d در نظر میگیریم. اگر ضریب تابع (a) مثبت باشد، برد تابع از d تا خواهد بود. اگر ضریب تابع (a) منفی باشد، برد تابع از d تا خواهد بود.
انواع تابع بر اساس دامنه
دامنه، مجموعهای از تمام ورودیهای قابل قبول برای قرار دادن در یک تابع و به دست آوردن خروجیهای آن تابع است. دامنه تابع، یکی از معیارهای مهم تقسیمبندی انواع تابع در ریاضی به شمار میرود. بر اساس این معیار، توابع ریاضی را میتوان به انواع مختلفی نظیر تابع جبری، تابع مثلثاتی، تابع لگاریتمی، تابع نمایی و غیره تقسیم کرد. در این بخش، به معرفی مهمترین انواع تابع در ریاضی بر اساس دامنه میپردازیم.
تابع جبری چیست ؟
«تابع جبری» (Algebraic Function)، تابعی متشکل از عبارتها و علائم جبری نظیر جمع، تفریق، ضرب، تقسیم، توان و جذر است. توابع جبری به سه گروه تابع چندجملهای، تابع گویا و تابع توانی تقسیم میشوند. توابع زیر را در نظر بگیرید:
تمامی توابع بالا، جبری هستند. توابع مثلثاتی، لگاریتمی و نمایی نیز در گروه توابع غیرجبری قرار میگیرند. در بخشهای قبلی، اغلب توابع جبری و برخی از توابع غیر جبری را معرفی کردیم. در ادامه، ضمن معرفی تابع توانی (به عنوان یکی از زیرمجموعههای اصلی توابع جبری)، تعاریف توابع غیرجبری را نیز ارائه میکنیم.
تابع توانی چیست ؟
«تابع توانی» (Power Function)، یکی از انواع توابع یکجملهای است. فرم کلی تابع توانی به صورت زیر نوشته میشود:
p، عضوی از مجموعه اعداد حقیقی بوده و k، هر عددی به غیر از ۰ است. توابع زیر را در نظر بگیرید:
توابع بالا در گروه توابع توانی قرار میگیرند؛ چراکه از یک عبارت با ضریب غیرصفر تشکیل میشوند. تصویر زیر، نمودار توابع توانی زوج و فرد را بر اساس علامت ضریب k نمایش میدهد.
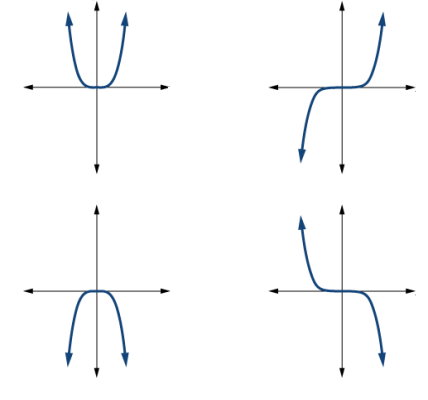
تابع مثلثاتی چیست ؟
«توابع مثلثاتی» (Trigonometric Functions)، توابعی هستند که رابطه بین زاویه و ضلعهای یک مثلث قائمالزاویه را نمایش میدهند. توابع سینوس، کسینوس، تانژانت، کتانژانت، سکانت و کسکانت، شش تابع مثلثاتی هستند.
برای آشنایی با توابع مثلثاتی، مثلث قائمالزاویه زیر را در نظر بگیرید.
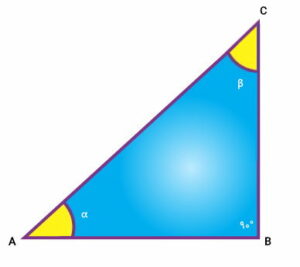
با توجه به ابعاد مثلث ABC، فرمول توابع مثلثاتی به صورت زیر نوشته میشود:
عبارتهای مورد استفاده در روابط بالا عبارت هستند از:
- A: زاویه راس A (یکی از زاویههای حاده مثلث قائمالزاویه)
- : سینوس زاویه راس A
- : کسینوس زاویه راس A
- : تانژانت زاویه راس A
- : کتانژانت زاویه راس A
- : سکانت زاویه راس A
- : کسکانت زاویه راس A
- BC: ضلع مقابل به زاویه راس A
- AB: ضلع مجاور به زاویه راس A
- AC: وتر مثلث قائمالزاویه
همانطور که مشاهده میکنید، ورودی توابع مثلثاتی، یک زاویه است. به عبارت دیگر، دامنه این نوع توابع، بر حسب زاویه نوشته میشود و در مجموعه اعداد حقیقی قرار دارد. این زاویه میتواند با یکای درجه یا رادیان باشد. جدول زیر، برد و دامنه شش تابع مثلثاتی را نمایش میدهد.
| تابع مثلثاتی | دامنه | برد |
توابع مثلثاتی، از مهمترین و کاربردیترین انواع تابع در ریاضی محسوب میشوند. مطالب مفید زیادی راجع به توابع مثلثاتی در مجله فرادرس تهیه شدهاند. در صورت علاقه به یادگیری راجع به این نوع از انواع تابع در ریاضی، مطالعه مطالب زیر را به شما پیشنهاد میکنیم:
- قوانین مثلثات به زبان ساده + مثال و تمرین
- نسبتهای مثلثاتی به زبان ساده + مثال و تمرین
- اثبات روابط مثلثاتی – به زبان ساده
- اتحادهای مثلثاتی + اثبات اتحادها و نمونه سوال با جواب
- روابط مثلثاتی و فرمولهای مثلثاتی مهم + دانلود PDF خلاصه رایگان
- مشتق توابع مثلثاتی | به زبان ساده
- انتگرال مثلثاتی – به زبان ساده + مثال و تمرین
- نمونه سوال مثلثات — همراه با جواب (+ دانلود فیلم آموزش رایگان)
- تقلب نامه (Cheat Sheet) مقادیر و فرمول های مثلثاتی
- تابع معکوس مثلثاتی — به زبان ساده
- مشتق توابع معکوس مثلثاتی — به زبان ساده
- معادلات مثلثاتی — به زبان ساده
- آموزش مثلثات — مجموعه مقالات جامع وبلاگ فرادرس
تابع لگاریتمی چیست ؟
یکی دیگر از انواع خاص تابع در ریاضی، «تابع لگاریتمی» (Logarithmic Function) است. فرم کلی تابع لگاریتمی به صورت زیر نوشته میشود:
یا
a، یک ثابت عددی بزرگتر از صفر، به غیر از یک است که به آن، پایه یا مبنای لگاریتم میگویند. اگر مبنای لگاریتم مشخص نشده باشد، آن را به صورت پیشفرض برابر با ۱۰ در نظر میگیرند. تابع لگاریتمی، وارون یک تابع با توان متغیر را نمایش میدهد. بر این اساس، رابطه بین پارامترهای موجود در معادله بالا را میتوان به صورت زیر نوشت:
توابع زیر، همگی از نوع لگاریتمی هستند:
تابع ، یکی از انواع توابع لگاریتمی است که با عنوان تابع لگاریتم طبیعی شناخته میشود. مبنای این تابع، عدد اویلر () است. دامنه توابع لگاریتمی، در مجموعه مثبت و غیرصفر اعداد حقیقی قرار دارد. از طرف دیگر، برد توابع لگاریتمی، میتواند هر عضوی از مجموعه اعداد حقیقی باشد. تصویر زیر، نمودار سه تابع لگاریتمی در پایههای مختلف نمایش میدهد.
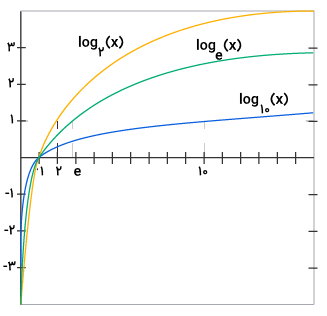
خواص تابع لگاریتمی چه هستند ؟
مهمترین مشخصات توابع لگاریتمی عبارت هستند از:
- و است.
- نمودار تابع لگاریتمی برای ، به صورت صعودی و برای ، به صورت نزولی است.
- دامنه تابع لگاریتمی، اعداد حقیقی بزرگتر از ۰ است.
- برد تابع تابع لگاریتمی، اعداد حقیقی است.
از خواص جبر توابع لگاریتمی میتوان به موارد زیر اشاره کرد:
سوالات متداول در رابطه با انواع تابع در ریاضی
در این بخش، به برخی از پرتکرارترین پرسشهای مرتبط با مبحث تابع و انواع تابع به صورت مختصر پاسخ میدهیم.
تعریف تابع چیست؟
تابع، رابطه بین دو مجموعه ورودی و خروجی است که هر یک از عضوهای مجموعه ورودی را تنها به یک عضو از مجموعه خروجی وصل میکند.
مهمترین انواع تابع در ریاضی کدام هستند ؟
از مهمترین انواع تابع در ریاضی میتوان به تابع چندجملهای، تابع گویا، تابع قدر مطلق، تابع مثلثاتی، تابع لگاریتمی، تابع جز صحیح و تابع همانی اشاره کرد.
انواع تابع بر اساس رابطه بین دامنه و برد کدام هستند؟
از انواع تابع در ریاضی بر اساس رابطه بین مجموعههای ورودی و خروجی میتوان به تابع یک به یک، تابع چند به یک، تابع پوشا، تابع یک به یک و پوشا، تابع غیرپوشا و تابع ثابت اشاره کرد.
انواع تابع بر اساس معادله کدام هستند؟
از انواع تابع در ریاضی بر اساس معادله میتوان تابع همانی، تابع خطی، تابع درجه دو یا مربعی، تابع درجه سه یا مکعبی و تابع چندجملهای را نام برد.
انواع تابع بر اساس بازه برد کدام هستند؟
انواع تابع در ریاضی بر اساس محدوده برد قابل قبول میتوان به تابع قدر مطلق، تابع گویا، تابع علامت، تابع فرد، تابع زوج، تابع متناوب یا دورهای، تابع جز صحیح، تابع وارون و تابع مرکب اشاره کرد.
انواع تابع بر اساس بازه دامنه کدام هستند؟
انواع تابع در ریاضی بر اساس محدوده دامنه قابل قبول میتوان تابع جبری، تابع مثلثاتی و تابع لگاریتمی را نام برد.
توابع چند جمله ای به چند نوع تقسیم می شوند ؟
توابع چندجملهای بر اساس تعداد عبارت به انواع یکجملهای، دوجملهای، سهجملهای و غیره تقسیم میشوند. از انواع این تابع بر اساس بزرگترین توان میتوان به تابع خطی، تابع درجه دو، تابع درجه سه و غیره اشاره کرد.
برد کدام یک از انواع تابع در ریاضی یک عضو دارد ؟
برد توابع ثابت و تابع صفر، تنها یک عضو دارد.
کدام یک از انواع تابع در ریاضی وارون یکدیگر هستند ؟
تابع لگاریتمی و نمایی، از نظر مفهومی، وارون یکدیگر هستند.
آزمون انواع تابع در ریاضی
۱. تابع ریاضی چه شرط اساسی میان ورودی و خروجی برقرار میکند؟
خروجیها الزاما بزرگتر از ورودیها هستند.
هر ورودی میتواند به چند خروجی مرتبط شود.
هر خروجی به بیش از یک ورودی تعلق دارد.
هر ورودی فقط به یک خروجی مرتبط میشود.
تعریف تابع بیان میکند که هر مقدار ورودی (x) دقیقا به یک خروجی (f(x)) اختصاص داده میشود، یعنی برای هر مقدار مجاز از دامنه، فقط یک نتیجه در برد وجود دارد. شرط اصلی تابع این است که هر ورودی دقیقا به یک خروجی اختصاص داشته باشد.
۲. فرمت معمول نمایش یک تابع و شرط تابع بودن یک رابطه ریاضی چیست؟
تابع به شکل جدول مقادیر x و y بیان میشود و هر خروجی میتواند چند ورودی داشته باشد.
تابع با رابطه x = f(y) تعریف شده و خروجیها اختیاری هستند.
تابع معمولا به صورت f(x) نوشته میشود و هر مقدار x فقط یک خروجی دارد.
تابع فقط زمانی تعریف میشود که x اعداد صحیح باشد و خروجی محدود باشد.
در نوشتار ریاضی، تابع معمولا به صورت f(x) نمایش داده میشود و قانون تابع تضمین میکند که هر مقدار از ورودی (x) به طور دقیق یک خروجی متناظر دارد.
۳. کدام عبارت درباره تفاوت دامنه، همدامنه و برد صحیح است و اهمیت آنها در تابع را بیان میکند؟
همدامنه همه خروجیهای ممکن است که تابع میتواند بدهد، ولی برد فقط مقادیر تولیدشده است.
دامنه مجموعهای از خروجیهای تابع است که واقعا تولید میشود.
برد مجموعهای از ورودیهای تابع است که میتوان در آن قرار داد.
دامنه و همدامنه همیشه با برد برابرند و تفاوتی ندارند.
دامنه شامل ورودیهای مجاز، همدامنه فضای کلی خروجیهای بالقوه و برد تنها مقادیر خروجی واقعی حاصل از تابع است. شناخت این تفاوتها برای تحلیل رفتار و ویژگیهای هر تابع اهمیت دارد.
۴. کدام گزینه معیار درست برای دستهبندی توابع ریاضی و اهمیت روابط دامنه و برد را بیان میکند؟
توابع بر اساس تعداد ریشهها و نمودارشان دستهبندی میشوند.
دستهبندی توابع میتواند بر اساس رابطه دامنه و برد، فرم معادله، ویژگی برد و نوع دامنه انجام شود.
برای دستهبندی توابع فقط باید برد آنها را در نظر گرفت.
تنها معیار دستهبندی توابع، شکل ظاهری نمودار آنها است.
دستهبندی توابع بر پایه رابطه دامنه و برد، فرم معادله، ویژگیهای برد و نوع دامنه امکانپذیر است. دستهبندی بر اساس رابطه دامنه و برد اهمیت دارد زیرا مشخص میکند که رفتار ورودی و خروجی تابع چگونه است و در حل مسائل خاص، نقش تعیینکنندهای ایفا میکند.
۵. برای تعیین دامنه، همدامنه و برد یک تابع ریاضی به چه روشی باید عمل کرد؟
تعیین دامنه تابع نیاز به دانستن معادله ندارد و با مشاهده خروجی کافی است.
همدامنه همواره برابر با دامنه است و تحلیل جداگانه لازم نیست.
فقط با مشاهده نمودار تابع میتوان دامنه و برد را به دست آورد.
با بررسی تعریف تابع و رابطه ریاضی آن میتوان دامنه، همدامنه و برد را تعیین کرد.
برای شناسایی دامنه، همدامنه و برد لازم است تعریف تابع و رابطه ریاضی آن بهطور تحلیلی بررسی شود. تعیین دامنه به مجموعه ورودیهایی بستگی دارد که تابع برای آنها مقدار دارد. همدامنه بر اساس تعریف تابع مشخص میشود و برد مجموعه خروجیهایی است که واقعا از تابع تولید میشود.
۶. کدام تفاوت کلیدی میان تابع یک به یک و تابع پوشا وجود دارد؟
در تابع یک به یک هر خروجی دقیقا با یک ورودی متناظر است، اما در تابع پوشا همه خروجیهای همدامنه حداقل یک پیشتصویر دارند.
در تابع پوشا هر ورودی فقط به خودش نگاشت میشود، اما در تابع یک به یک چند ورودی میتوانند یک خروجی داشته باشند.
تابع پوشا فقط برای توابع درجه دو تعریف میشود، اما تابع یک به یک برای هر نوع تابع ممکن است.
تابع یک به یک فقط برای اعداد مثبت تعریف میشود، اما تابع پوشا در همه اعداد حقیقی برقرار است.
ویژگی تابع یک به یک این است که نتیجه هر مقدار ورودی یکتا بوده و خروجی تکراری وجود ندارد. یعنی هر خروجی دقیقا مربوط به یک ورودی است. در مقابل، تابع پوشا ویژگی دارد که هر عضو همدامنه باید حداقل یک خروجی تابع شود و هیچ عضو بدون پیشتصویر نباشد.
۷. کدام ویژگی به شناسایی تابع ثابت و نمودار آن کمک میکند؟
هر ورودی مقدار خروجی متفاوت دارد و نمودار افزایشی است.
نمودار همیشه یک خط افقی است و مقدار خروجی تغییر نمیکند.
نمودار دارای شیب مثبت بوده و مقدار خروجی با x رشد میکند.
نقاط نمودار فقط روی محور y قرار دارند و x تاثیری ندارد.
ویژگی مشخص تابع ثابت آن است که صرفنظر از مقدار x، خروجی همواره برابر با یک مقدار ثابت میشود. مطابق این خاصیت، نمودار تابع ثابت یک خط افقی روی محور y است و مقدار خروجی تغییر نمیکند.
۸. کدام عبارت نقش علامت مشتق را در تعیین صعودی یا نزولی بودن یک تابع به درستی بیان میکند؟
وقتی مشتق تابع منفی یا صفر باشد، تابع همواره صعودی است.
اگر مشتق تابع مثبت یا صفر باشد، تابع صعودی است.
تابع صعودی همیشه مشتق منفی دارد.
مشتق تابع فقط برای توابع ثابت اهمیت دارد.
علامت مشتق تابع نشان میدهد که تابع در آن بازه چگونه رفتار میکند. اگر مشتق مثبت یا صفر باشد، تابع در آن بازه صعودی در نظر گرفته میشود. اگر مشتق منفی باشد، تابع نزولی است. این شرط فقط به علامت مشتق بستگی دارد و ربطی به توابع ثابت یا فقط رفتار صعودی ندارد.
۹. فرم کلی تابع چندجملهای چیست و چه تفاوت اصلی میان تابع خطی، درجه دو و درجه سه وجود دارد؟
تابع چندجملهای مجموع جملاتی با توانهای مختلف x است. تابع خطی بیشترین توانش یک، درجه دو بیشترین توانش دو و درجه سه بیشترین توانش سه است.
تابع چندجملهای فقط ضرب چند عدد ثابت است. نوع خطی، درجه دو و درجه سه هیچ تفاوتی در تعداد جملات ندارند.
تابع چندجملهای فقط شامل ضرب x با ضرایب ثابت است. نوع خطی دارای مقدار ثابت، درجه دو بدون مقدار ثابت و درجه سه فقط با یک جمله است.
تابع چندجملهای فقط توانهای زوج x دارد. نوع خطی دارای توان دو، درجه دو دارای توان چهار و درجه سه دارای توان شش است.
فرم کلی تابع چندجملهای عبارت است از مجموع جملاتی که در آنها x به توانهای مختلف (مانند صفر، یک، دو، سه) ضرب در ضرایب عددی آمده است. تفاوت اصلی در این است که در تابع خطی، بیشترین توان x یک است. در تابع درجه دو، بیشترین توان x دو است. و در تابع درجه سه، بیشترین توان x سه است. گزینههای دیگر نادرست هستند، زیرا یا به توانهای خاصی محدود میشوند یا تعریف کلی تابع چندجملهای را رعایت نمیکنند.
۱۰. برای پیدا کردن معادله خط عبوری از دو نقطه متفاوت با مختصات معلوم، چه باید کرد؟
شیب خط را معکوس کنید و سپس معادله یک خط عمود بر خط موردنظر را بنویسید.
فقط کافی است مقادیر x هر دو نقطه را جمع و تقسیم بر دو کنید و آن را جایگزین x در معادله خط کنید.
معادله خط را صرفا با قرار دادن نقطه وسط دو نقطه به دست آورید.
شیب خط را با استفاده از مختصات دو نقطه محاسبه و سپس معادله را با قرار دادن یکی از نقطهها بنویسید.
برای بدست آوردن معادله خطی که از دو نقطه با مختصات معلوم عبور میکند باید ابتدا شیب خط را بر اساس تفاوت مقدار y و x دو نقطه محاسبه کرد و سپس نقطهای از دو نقطه را همراه با شیب در فرم معادله خط قرار داد.
۱۱. کدام گزاره درباره اجزای کلیدی نمودار تابع درجه دو درست است و نقش آنها در تحلیل رفتار تابع را نشان میدهد؟
راس نقطهای است که کمینه یا بیشینه تابع را نشان میدهد و تحلیل جهت بازشدگی منحنی با آن ممکن است.
ریشهها همیشه نمایشگر نقاطی هستند که تابع مقدار بیشینه میگیرد.
محور تقارن خطی است که نمودار را به دو بخش مساوی تقسیم میکند اما موقعیت راس را مشخص نمیکند.
محور تقارن تنها جهت بازشدگی منحنی را تعیین میکند و ارتباطی با راس ندارد.
راس، نقطهای است که تابع درجه دو در آن به کمترین یا بیشترین مقدار خود میرسد و تعیین این نقطه برای تحلیل رفتار کلی منحنی بسیار مهم است. موقعیت راس همچنین به کمک محور تقارن قابل محاسبه است. محور تقارن خطی است که از راس عبور میکند و نمودار را به طور مساوی تقسیم میکند و نقش تعیینکنندهای در جایگاه راس دارد.
۱۲. برای بدست آوردن ریشههای یک تابع درجه دو چه روشی استفاده میشود؟
استفاده از جدول مقادیر برای یافتن خروجیهای مثبت
رسم نمودار خطی تابع و بررسی نقاط تقاطع
بدست آوردن مقدار تابع برای x=0
حل معادله با فرمول درجه دو که شامل دلتا است.
برای بدست آوردن ریشههای تابع درجه دو باید از فرمول خاصی که دلتا را شامل میشود استفاده کرد. این روش با قرار دادن ضرایب معادله و استفاده از دلتا، نقاطی که خروجی تابع برابر صفر است را پیدا میکند. بدست آوردن مقدار تابع فقط برای x=0 جایگزین مناسبی نیست، زیرا باید تمام ریشهها بررسی شوند. استفاده از جدول مقادیر ریشه را دقیق به دست نمیدهد و فقط مقادیر نمونه را نشان میدهد. رسم نمودار خطی روی تابع درجه دو کاربرد ندارد زیرا این توابع نمودار سهمی دارند.
۱۳. کدام ویژگی تابع قدرمطلق باعث تفاوت برد آن با توابع دیگر میشود؟
خروجی تابع میتواند مثبت و منفی باشد.
خروجی تابع فقط برای مقادیر صحیح تعریف میشود.
خروجی تابع همیشه کمتر از صفر است.
خروجی تابع همیشه بزرگتر یا مساوی صفر است.
تابع قدرمطلق همیشه خروجی غیرمنفی تولید میکند و هیچگاه مقدار منفی نمیگیرد، به همین دلیل برد آن فقط شامل اعداد بزرگتر یا مساوی صفر است. دلیل تفاوت این تابع با بسیاری از توابع دیگر این است که میتوانند خروجی منفی داشته باشند.
۱۴. برای تعیین دامنه و برد یک تابع گویا چه روشی براساس مخرج کسر باید به کار برد؟
تمام اعداد حقیقی به جز صفر، همواره دامنه توابع گویا هستند و برد برابر دامنه است.
ورودیهایی که مخرج را صفر میکنند از دامنه حذف میشوند و برد با توجه به مقدار خروجیهای ممکن محاسبه میشود.
دامنه و برد توابع گویا بدون توجه به مخرج، مجموع تمام عددهای حقیقی هستند.
در توابع گویا دامنه مجموعه اعدادی است که صورت برابر صفر نمیشود و برد همان مقادیر مثبت است.
هر عددی که جایگذاری آن در مخرج تابع گویا باعث صفر شدن مخرج شود از دامنه حذف میشود، زیرا تقسیم بر صفر تعریفنشده است. بنابراین دامنه برابر تمام اعداد حقیقی به جز نقاطی است که مخرج صفر میشود. برد نیز با توجه به خروجیهای واقعی تابع و تاثیر محدودیت دامنه مشخص میگردد.
۱۵. برای اینکه یک تابع در ریاضی زوج یا فرد باشد، چه ویژگیهایی باید داشته باشد و تفاوت اصلی آنها چیست؟
تابع زوج نسبت به محور y متقارن است و برای همه x داریم f(-x) = f(x)، اما تابع فرد نسبت به مبدا متقارن است و f(-x) = -f(x) برقرار است.
تابع زوج دارای شیب مثبت ثابت است و تابع فرد شیب متغیر دارد.
تابع زوج فقط برای مقادیر مثبت x و تابع فرد برای مقادیر منفی x تعریف میشود.
تابع زوج هیچ نقطه اشتراک با محور x ندارد، اما تابع فرد همیشه محور x را قطع میکند.
یک تابع زمانی زوج محسوب میشود که نسبت به محور y متقارن باشد و شرایط f(-x) = f(x) را برای همه x دارا باشد. تابع فرد نسبت به مبدا متقارن است و ویژگی مشخصه آن این است که f(-x) = -f(x) برای همه x برقرار است.
۱۶. کدام عبارت بیانگر مراحل صحیح وارونگیری تابع یک به یک است؟
یافتن دامنه تابع بدون توجه به برد
رسم نمودار تابع و یافتن نقاط اشتراک با محور x
جایگذاری مقدار دلخواه به جای x و محاسبه f(x)
تعویض جای x و f(x) و حل معادله جدید برای x
عبارت «تعویض جای x و f(x) و حل معادله جدید برای x» مراحل درست وارونگیری تابع یک به یک را بیان میکند. باید ابتدا x و f(x) را جابجا کرد و معادله را نسبت به x حل نمود تا تابع وارون به دست آید.
۱۷. کدام عبارت تفاوت اصلی میان تابع جبری و غیرجبری و زیرمجموعههای تابع جبری را به درستی بیان میکند؟
تابع غیرجبری فقط از جمع و ضرب تشکیل میشود و تابع جبری شامل نوع لگاریتمی است.
زیرمجموعههای تابع جبری فقط توابع مثلثاتی را دربر میگیرند و تابع جبری حاصل تقسیم دو تابع است.
تابع غیرجبری مقدار ثابت دارد و تابع جبری همواره مقدار متغیر تولید میکند.
تابع جبری از چهار عمل اصلی ساخته میشود و زیرمجموعههای آن چندجملهای، توانی و گویا هستند.
طبق توضیحات، تابع جبری با استفاده از جمع، تفریق، ضرب، تقسیم، توان و جذر ساخته میشود و شامل زیرمجموعههایی مانند چندجملهای، گویا و توانی است. در مقابل، توابع غیرجبری مانند توابع مثلثاتی یا لگاریتمی هستند که با اعمال غیرجبری تعریف میشوند.
۱۸. کدام جمله درباره تابع لگاریتمی صحیح است؟
دامنه تابع لگاریتمی تمام اعداد حقیقی است و تقسیم لگاریتمها برابر جمع آنهاست.
برد تابع لگاریتمی اعداد حقیقی مثبت است و توان لگاریتم جمع دو عدد است.
دامنه تابع لگاریتمی اعداد حقیقی مثبت است و جمع لگاریتمها برابر لگاریتم ضرب آنهاست.
برد تابع لگاریتمی فقط اعداد منفی است و ضرب لگاریتمها برابر لگاریتم اختلاف آنهاست.
در تابع لگاریتمی، مقدار x باید حقیقی و مثبت باشد تا لگاریتم تعریف شود، بنابراین دامنه تابع لگاریتمی اعداد حقیقی مثبت است. همچنین یکی از مهمترین خواص جبر لگاریتم این است که جمع دو لگاریتم با پایه یکسان برابر لگاریتم ضرب آنها است.













خیلی عالی بود معلومه کلی براش زحمت کشیدید واقعا خسته نباشید. کاش مجدد یکم وقت بذارید بعضی جاهاش هم تکمیل تر بشه و غلط هاش گرفته بشه. در کل عالی بود خدا خیرتون بده
باسلام
در اول درس که دو تابع را باهم مقیایسه میکنیم
f(x)=x-4 این منفی 4 نیست بلکه 1 هست چون در تصویر پایین به ازای مقادیرx اگر منفی 4 قراربدهیم جوابهای f(x) درست در نمیاید.
باتشکر
با سلام و وقت بخیر؛
ممنون از توجه شما. رابطه اصلاح شد.
از همراهی شما با مجله فرادرس سپاسگزاریم.
با عرض سلام و خسته نباشید،، خیلی عالی بود، تمام ابهاماتم درباره ی توابع رفع شد،، ممنون از زحماتتون🙏🏻🌹
توضیحات بسیار عالی بودند.
فقط یک اشتباهی در توضیحات ‘توابع گویا’ هست،
“ به عنوان مثال، تمام توابع زیر، در گروه توابع گویا قرار میگیرند” سومي كه h(x) هست جزو توابع گويا قرار ميگيرند! اما دقيقا همون مثال خط پايينش f(x) جزو توابع گویا نیستن چون “ مخرج هیچ کسری نمیتواند برابر با صفر باشد”!!!
درحالیکه صورت هر دو کسر يكي و همچنین مخرج هم در دومثال یکی هستند!
شايد اشتباه تايپي هست يا شايد هم من اشتباه ميكنم.
ممنون ميشم پاسخ بديد🙏🏻
با سلام و احترام؛
این مورد بازبینی و اصلاح شد.
از همراهی شما با مجله فرادرس سپاسگزاریم.