تابع یکنوا چیست؟ — از صفر تا صد

«توابع» (Functions) و «رابطه‌ها» (Relations) در ریاضیات نقش مهمی برای نمایش ارتباط بین دو (یا چند) متغیر دارند. در حقیقت تابع، بیان مدل‌بندی شده از یک ارتباط یا پیوند بین متغیرها است. در نوشتارهای مختلف از مجله فرادرس با توابع مختلف ریاضی آشنا شده‌ایم. در این نوشتار می‌خواهیم بدانیم تابع یکنوا چیست و چه خصوصیاتی دارد.

برای آشنایی بیشتر با مفهوم تابع و ویژگی‌های اصلی آن بهتر است نوشتارهای مفاهیم تابع – به زبان ساده و رابطه و تابع از نگاه مجموعه‌ ها — به زبان ساده را مطالعه کنید. همچنین مطالعه مجموعه ها در ریاضیات – مفاهیم پایه و ضرب دکارتی مجموعه ها و مختصات دکارتی — به زبان ساده نیز خالی از لطف نیست.

تابع یکنوا چیست؟

در ریاضیات، «تابع یکنوا» (Monotone Function)، تابعی است که در «مجموعه‌های ترتیب دار» (Ordered Sets) یا ترتیبی، تعریف شده و این ترتیب نیز برای مقادیر تابع یکنوا براساس مقادیر مجموعه‌های مربوط به دامنه تابع، حفظ می‌شود. به چنین توابعی «حافظ ترتیب» (Preserve Order) نیز گفته می‌شود.

فیلم آموزش حسابان ۲ – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

ما با توابع یکنوا در ریاضیات و هندسه تحلیلی یا حسابان (Calculus)، زمانی که در مورد توابع حقیقی صحبت می‌کنیم، به کررات مواجه شده‌ایم. لگاریتم، تابع نمایی و ... همگی مثال‌هایی از توابع یکنوا هستند. ولی در این متن، علاوه بر مشخص کردن خصوصیات چنین توابعی، حالت پیشرفته و تعمیم توابع یکنوا در مباحث مربوط به «نظریه ترتیب» (Order Theory) نیز مورد تحلیل و بررسی قرار می‌گیرد.

تابع یکنوا در حسابان

قبل از هر چیز برای درک ویژگی‌های تابع یکنوا، به بررسی «تابع صعودی» (Increasing Function) و «نزولی» (Decreasing Function) می‌پردازیم.

تابع صعودی: فرض کنید تابع $$f$$ یک تابع صعودی است. به این ترتیب تغییرات متغیر و تابع در آن به یک جهت یا یک راستا است. در نتیجه هر وقت که مقدار متغیر $$x$$، کاهش یابد، تابع $$f$$ نیز کاهش یافته یا تغییری نمی‌کند و هر وقت متغیر $$x$$، افزایش یابد، تابع $$f$$‌ نیز افزایش یافته یا تغییری نخواهد کرد.

نکته: اگر با افزایش متغیر، تابع نیز حتما در همان راستا تغییر یابد (هر چند به میزان کم) تابع را «اکیدا صعودی» (Strictly Increasing) می‌گوییم.

تابع نزولی: تابعی که جهت تغییرات متغیر و تابع عکس یکدیگر باشد، تابع نزولی نامیده می‌شود. به این معنی که با افزایش مقدار متغیر، تابع یا ثابت بوده یا کاهش خواهد یافت. از طرفی اگر متغیر کاهش داشته باشد، تابع ثابت بوده یا افزایش می‌یابد.

نکته: اگر با افزایش یا کاهش متغیر، تابع نیز حتما برعکس آن تغییر یابد (هر چند به میزان کم) تابع را «اکیدا نزولی» (Strictly Decreasing) می‌گوییم.

حال به معرفی تابع یکنوا براساس خاصیت صعودی یا نزولی بودن تابع، خواهیم پرداخت.

تابع یکنوا و ارتباط آن با تابع صعودی و نزولی

تابع $$f$$ روی زیر مجموعه‌ای از اعداد حقیقی را یک تابع یکنوا گویند اگر و فقط اگر روی همه دامنه‌اش، نزولی یا صعودی باشد. به این ترتیب مشخص می‌شود که توابعی که به عنوان تابع صعودی می‌شناسیم، یکنوا نیز هستند. همچنین توابع نزولی، یکنوا محسوب خواهند شد. البته توجه داشته باشید که در اینجا اگر تابع اکیدا نزولی یا اکیدا صعودی باشد، آن را تابعی اکیدا یکنوا می‌گویند.

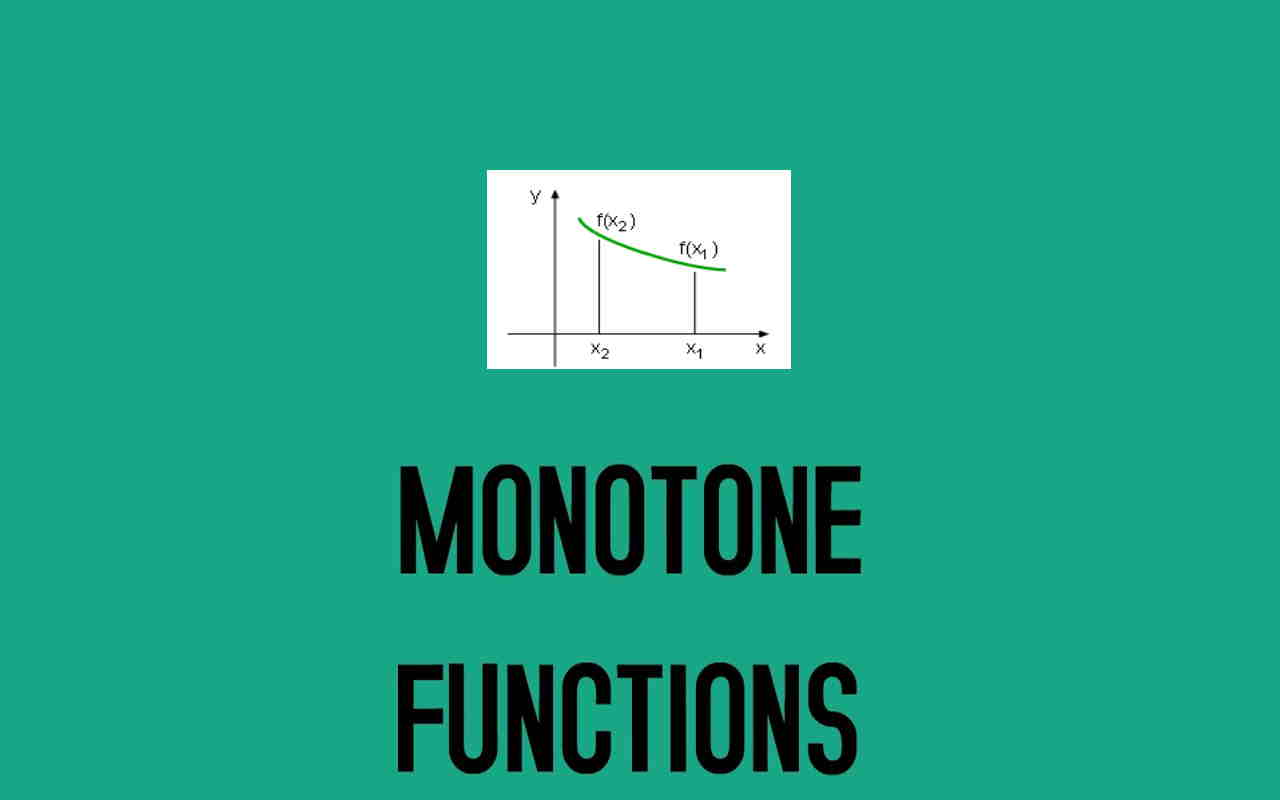
برای مثال تابعی که در تصویر ۱ دیده می‌شود را در نظر بگیرید. واضح است که این تابع در همه دامنه‌اش، تابعی صعودی (و نه اکیدا صعودی) است. در نتیجه چنین تابعی را یکنوا خواهیم خواند.

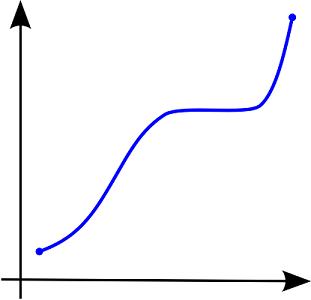
همچنین در تصویر ۲ نیز نمونه‌ای از تابع یکنوا را مشاهده می‌کنید که به صورت یک تابع نزولی (و نه اکیدا نزولی) در دامنه‌اش ترسیم شده است.

نکته: چیزی که برای یک تابع یکنوا مهم است، تغییر در جهت یا خلاف جهت تغییرات متغیر است. البته ممکن است در بعضی از بازه‌های دامنه، تابع تغییری نداشته باشد ولی همیشه تابع یکنوا از یک روند مشخص پیروی می‌کند.

به این ترتیب تابع یکنوا را براساس تعریف تابع صعودی یا نزولی می‌توان تعریف کرد.

$$ \large  x_1 , x_2 \in D_f ,\; \; \; {x_1}\;^>_{<} \; {x}_2 \rightarrow f(x_1) \; ^{\geqslant}_{\leqslant} \; f(x_2)\;\;\; $$:تعریف تابع یکنوا براساس تابع صعودی

$$ \large  x_1 , x_2 \in D_f ,\; \; \; {x_1}\;^>_{<} \; {x}_2 \rightarrow f(x_1) \; ^{\leqslant}_{\geqslant} \; f(x_2)\;\;\;\; $$:تعریف تابع یکنوا براساس تابع نزولی

نکته: تابعی که اکیدا صعودی یا اکیدا نزولی باشد، تابع «اکیدا یکنوا» (Strictly Monotone) نامیده می‌شود. در این صورت رابطه‌های بالا به صورت زیر نوشته خواهند شد. به علامت‌های بزرگتر یا کوچکتر اکید توجه داشته باشید.

$$ \large  x_1 , x_2 \in D_f ,\; \; \; {x_1}\;^>_{<} \; {x}_2 \rightarrow f(x_1) \; ^{>}_{<} \; f(x_2)\;\;\; $$:تعریف تابع اکیدا یکنوا براساس تابع اکیدا صعودی

$$ \large  x_1 , x_2 \in D_f ,\; \; \; {x_1}\;^>_{<} \; {x}_2 \rightarrow f(x_1) \; ^{<}_{>} \; f(x_2)\;\;\;\; $$:تعریف تابع اکیدا یکنوا براساس تابع اکیدا نزولی

تابع غیر یکنوا

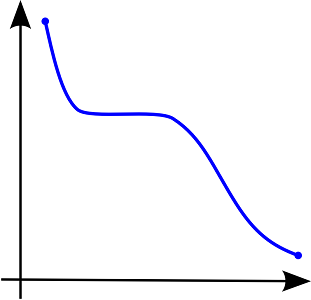
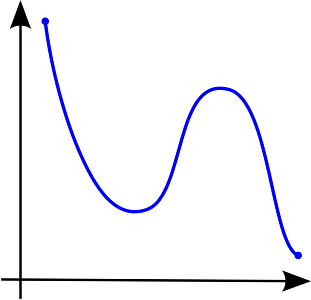
بعضی از توابع در ریاضیات، یکنوا نیستند. به چنین توابعی، غیریکنوا گفته می‌شد. واضح است که تابعی نمایش داده شده در تصویر ۳، یک تابع یکنوا نیست، زیرا در بعضی از قسمت‌های دامنه، صعودی در قسمتی دیگر، صعودی است.

فیلم آموزش ریاضی ۳ – پایه دوازدهم علوم تجربی در فرادرس

کلیک کنید

در نتیجه نمی‌توان آن را در همه دامنه‌اش با تغییرات یکسان یا مخالف با تغییرات متغیر در نظر گرفت. واضح است که گاهی این تغییرات همسو و در زمانی دیگر، عکس تغییرات متغیر است. در بعضی از کتاب‌ها، چنین توابعی را «نایکنوا»(Non-monotonic) نیز می‌نامند.

معکوس تابع یکنوا

به یاد دارید که منظور از معکوس تابع، تغییر ضابطه تابع است به طوری که بتوان متغیر را برحسب یک تابع جدید بدست آورد. به بیان ریاضی این وضعیت را به شکل زیر نمایش می‌دهیم.

$$ \large f^{-1}(y) = x , \;\;\; f^{-1}(f(x)) = x $$

رابطه ۱

این امر به معنی جابجایی متغیر و تابع در زوج مرتب، است. اگر معکوس تابع، دارای خصوصیات تابع نیز باشد، آن را تابع معکوس $$f$$ می‌نامند در غیر اینصورت اغلب از عبارت «معکوس تابع» (Function Inverse) استفاده می‌شود. در ضمن اگر خط نیم‌ساز ربع اول را ترسیم کنیم، تابع و معکوس آن نسبت به این خط تقارن خواهند داشت. به این ترتیب کافی است هر نقطه از منحنی تابع را به این نیم‌ساز عمود کرده و به اندازه خودش، امتداد دهیم تا منحنی معکوس تابع شکل گیرد. به تصویر ۴ توجه کنید.

نکته: براساس نمودار، منحنی را یک تابع می‌گویند که خطوط موازی محور عمودی، منحنی را در حداکثر یک نقطه قطع کند. در غیر اینصورت، چنین رابطه‌ای، یک تابع نخواهد بود.

برای مثال تابعی را مانند $$f(x)$$ با ضابطه زیر در نظر بگیرد. نمودار مربوط به منحنی این تابع که در تصویر ۴ ترسیم شده، صعودی و در نتیجه یکنوا است. ولی با توجه به خط عمودی رسم شده روی محور افقی، معکوس آن نمی‌تواند تابع باشد. در نتیجه تابع چند ضابطه‌ای $$f(x)$$، معکوس‌پذیر نیست و معکوس آن تابع نخواهد بود.

$$ \large f(x) = \begin{cases} x^3 &, 0.0 \leq x < 0.5 \\ 0.125&,  0.5 \leq x < 0.7 \\ (x - 0.2)^3&, \;\;\;\;\;\;\;\;\;\;\; x \geq 0.7 \end{cases} $$

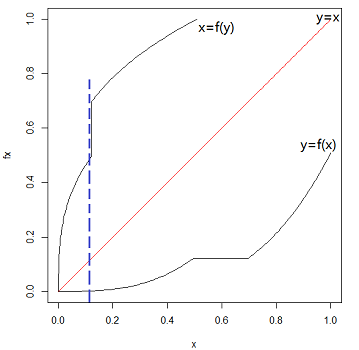
به این ترتیب می‌توان گفت که شرط معکوس‌پذیری یک تابع، اکیدا یکنوا بودن است. این حالت از تابع را گاهی «یک به یک» (Injective Function) نیز می‌نامند.

تبدیلات یکنوا

عبارت تبدیل یکنوا (Monotonic Transformation)  اغلب معرف تبدیل یا تابعی است که به صورت اکیدا صعودی عمل می‌کند. چنین تبدیلی باعث می‌شود که رابطه ترتیبی حفظ شده و با افزایش مولفه یا ارگومان تبدیل، نتیجه حاصل از تبدیل نیز افزایش یابد. به همین مناسبت در چنین مواردی، تبدیل یکنوا (صعودی) را «تبدیل یکنوای مثبت» (Positive Monotonic Transformation) می‌نامند. در مقابل اگر تبدیل، براساس یک رابطه نزولی تعریف شده باشد، تبدیل یکنوا را به نام «تبدیل یکنوای منفی» (Negative Monotonic Transformation) به کار می‌برند.

چنین تبدیلاتی (مانند تبدیل لگاریتمی یا تبدیل نمایی) بخصوص در حوزه اقتصاد و فیزیک به کار رفته و حتی در تغییر متغیر در «مدل‌سازی رگرسیونی» (Regression Modeling) و محاسبات مربوط به «برآوردگر درستنمایی» (Likelihood Estimator) در آمار نیز کاربرد دارند. به یاد داشته باشید که چنین تبدیل‌هایی، حافظ ترتیب هستند.

ویژگی‌ها و کاربردهایی از توابع یکنوا

در ادامه به بعضی از خصوصیات توابع یکنوا و کاربرد آن‌ها در حوزه‌های خاص علمی اشاره خواهیم کرد. البته در اینجا به توابع حقیقی یکنوا اشاره داریم که دامنه و برد آن‌ها «مجموعه اعداد حقیقی» هستند.

• تابع یکنوا، دارای حد راست و چپ در هر نقطه از دامنه‌ است.
• حد تابع یکنوا در مثبت بی‌نهایت یا منفی بی‌نهایت یا یک عدد حقیقی است یا نامتناهی (بی‌نهایت) است.
• تابع یکنوا، ممکن است شمارا نقطه ناپیوستگی یا پرش داشته باشد.

به دلیل ویژگی‌هایی که برای تابع یکنوا گفته شد، تابع یکنوا بخصوص در «آنالیز ریاضی» (Mathematical Analysis) نقش مهمی ایفا می‌کند. این خواص در حوزه آنالیز ریاضی به صورت فهرست زیر معرفی می‌شوند.

• اگر تابع $$f$$، یکنوا روی بازه‌ای مثل $$I$$ باشد، آنگاه این تابع روی چنین فاصله‌ای تقریبا همه جا، مشتق‌پذیر است. به این ترتیب اگر مجموعه نقطه‌های مشتق‌ناپذیری چنین تابعی را $$S$$ در نظر بگیریم، اندازه لبگ مجموعه $$S$$، برابر با صفر خواهد بود.
• اگر مجموعه نقاط مشتق‌ناپذیر تابع یکنوای $$f$$، شمارا باشد، آنگاه تابع $$f$$، «مطلقا پیوسته» (Absolute Continuous) است.
• اگر تابع $$f$$ روی بازه $$[a,b]$$ یکنوا باشد، آنگاه $$f$$ را «انتگرال‌پذیر ریمان» (Reimann Integrable) می‌گویند.

همچنین کاربردهای مختلفی از توابع یکنوا در ریاضیات می‌توان برشمرد. حتی در مباحث خارج از حوزه ریاضیات نیز، تابع یکنوا اهمیت زیاد و کاربردهای مهمی دارد.

• ویژگی تابع توزیع احتمال تجمعی: از کاربردهای مهم برای توابع یکنوا می‌توان به «نظریه احتمال» (Probability Theory) و مباحث مربوط به متغیر تصادفی و توزیع و چگالی آن، اشاره کرد. اگر $$X$$، یک متغیر تصادفی (Random Variable) باشد، «تابع احتمال تجمعی» (Cumulative Distribution Function) آن که به صورت $$ F_X(x) = \Pr ( X \leq x) $$ تعریف و محاسبه می‌شود، تابعی یکنوا و صعودی است.
• تابع تک‌نمایی: در ریاضیات، تابع $$f$$ را «تک نمایی» (Unimodal) می‌گوییم اگر تا یک نقطه (که معمولا نما- mode نامیده می‌شود) یکنوا و صعودی بوده و از آن نقطه به بعد یکنوا ولی نزولی شود.
• تابع یک به یک: اگر تابعی مانند $$f$$، «اکیدا یکنوا» (Strictly Monotonic) باشد، می‌توان آن را یک «تابع یک به یک» (Injective) روی دامنه‌اش در نظر گرفت. در این صورت اگر $$T$$ برد تابع $$f$$ ‌باشد، می‌توان تابعی پیدا کرد که معکوس تابع $$f$$‌ بوده و ترکیب آن با تابع $$f$$، یک تابع همانی باشد. به رابطه ۱ توجه کنید. از طرفی هر «تابع ثابت» (Constant Function)، یکنوا بوده ولی یک به یک نیست و در نتیجه معکوس‌پذیر نیز نخواهد بود.

یکنوایی در نظریه ترتیب

در «نظریه ترتیب» (Order Theory) به مفهوم ترتیب و «ترتیب جزئی» (Partial Ordered) روی مجموعه‌ها برخورد می‌کنیم. همچنین موضوع «پیش‌ترتیب» (Preorderd) در مجموعه اعداد حقیقی نیز در نظریه ترتیب مطرح می‌شود.

فیلم آموزش ریاضیات گسسته – پایه دوازدهم در فرادرس

کلیک کنید

تعریفی که برای توابع یکنوا در حسابان مطرح شد در این موضوعات و حوزه نظریه ترتیب نیز به کار می‌رود. البته در نظریه ترتیب، از عبارت‌های صعودی یا نزولی استفاده نمی‌شود در عوض، رابطه کوچکتری یا بزرگتری (به صورت عادی یا اکید) به کار خواهد رفت.

فرض کنید نماد $$\leq$$ یک رابطه ترتیب جزئی را روی مجموعه‌های مرتب جزئی نشان دهد. در این حالت تابع یکنوا، تابعی است که «حافظ ترتیب» (Order-Preserve) یا اصطلاحاً «هم‌نوا» (Isotone) باشد. در این صورت چنین تابعی باید در شرط زیر صدق کند.

$$ \large x \leq y \rightarrow f(x) \leq f(y) $$

واضح است که $$x, y $$ باید در دامنه تابع $$f$$ قرار داشته باشند.

نکته: توجه داشته باشید که ترکیب دو تابع یا نگاشت یکنوا، باز هم یکنوا است.

در مقابل نماد دوگان (Dual Notation) یا برعکس، برای نمایش توابع «ضد-یکنوا» یا «عکس ترتیب» (Order-reversing) است، اگر در شرط زیر صادق باشد.

$$ \large x \leq y \rightarrow f(y) \leq f(x) $$

بر این اساس، «تابع ثابت» (Constant Function)، هم یک تابع یکنوا و هم تابع ضد-یکنوا است. اگر تابع $$f$$، هم یکنوا و هم ضد-یکنوا بوده و دامنه‌اش نیز یک «مشبکه» (Lattice) باشد، آنگاه حتما یک تابع ثابت خواهد بود.

توابع یکنوا مرکز مباحث مربوط به نظریه ترتیب هستند. از چنین توابعی در بیشتر مقاله‌ها با موضوع نظریه ترتیب استفاده می‌شود. همچنین مثال‌های به کار رفته در این نظریه، اغلب براساس توابع یکنوا صورت می‌گیرد. توابع یکنوا مورد استفاده در این حوزه اغلب توابعی هستند که دارای خاصیت «هم‌ریختی ترتیبی» (Order Isomorphisms) یا «ترتیب درونی» (Order embedding) هستند.

تابع یکنوا در زمینه الگوریتم‌های جستجوی اکتشافی

در حوزه مطالعاتی الگوریتم‌های جستجو، یکنوایی یا «ثبات» (Consistency) یک شرط برای «توابع الگوریتم‌های جستجوی اکتشافی» (Heuristic Function) محسوب می‌شود.

یک تابع اکتشافی مانند $$h(n)$$، یک تابع یکنوا است اگر برای هر گره مثل $$n$$ و هر گره بعدی از آن، برآورد هزینه رسیدن به هدف از گره $$n$$ بزرگتر از گام هزینه رسیدن به $$n'$$ بعلاوه هزینه رسیدن به هدف از گره $$n'$$ نباشد. به این ترتیب داریم:

$$ \large h(n) \leq c(n, a, n') + h(n') $$

واضح است که رابطه بالا براساس «نامساوی مثلثی» (Triangle Inequity)، برحسب $$n , n' $$ و تابع هدف $$G_n$$ نزدیکتر به $$n$$، نوشته شده است. از آنجایی که هر یک از توابع یکنوا در الگوریتم اکتشافی، مجاز (Admissible) یا پذیرفتنی هم هستند، یکنوا بودن شرط اولیه و اصلی برای توابع به کار رفته در الگوریتم‌های جستجوی اکتشافی محسوب می‌شود. از الگوریتم‌های معروف جستجوی اکتشافی می‌توان به روش *A اشاره کرد که بهینه بودن آن توسط یکنوا بودن تابع اکتشاف، قابل اثبات است.

یکنوایی در توابع بولی

در جبر بولی و حساب باینری یا دو دویی، تابع یکنوا، تابعی مثل $$f$$ است که برای هر $$a_i$$ و $$b_i$$ در مجموعه $$\{ 0 , \}$$ با شرط «ضرب دکارتی مرتب شده مختصاتی» (Cartesian Product $$\{0,1\}^n$$) روی این مجموعه (که به صورت ترتیبی است)، دارای مقادیری با همان ترتیب باشند. این ویژگی را به بیان ریاضی به صورت زیر نشان می‌دهیم.

$$ \large a_1 \leq b_1 , a_2 \leq b_2 , \ldots , a_n \leq b_n \rightarrow f(a_1, a_2 , \ldots, a_n) \leq f(b_1 , b_2 , \ldots ,b_n) $$

به بیان دیگر یک تابع بولی به شرطی یکنوا است که هر ترکیبی از ورود‌های آن (که شامل مقادیر صحیح  -True- یا نادرست -False- است)، زمانی که «نادرست» (False) به «صحیح» (True) تبدیل شود، خروجی فقط از نادرست (False) به صحیح (True) تبدیل شود. در حقیقت در این حالت خروجی نباید از True به False تغییر یابد.

این چنین تابعی در نمودار درختی مطابق با تصویر ۵ خواهد بود. همانطور که دیده می‌شود در این درخت (نمودار هسه یا Hasse Diagram)، هیچ ترکیبی از مقدارهای ۰ و ۱ تبدیل به ۰ نمی‌شود، در نتیجه هیچگاه مقدار صحیح (با برچسب ۱) در زیر مقدار نادرست (با برچسب صفر) قرار نمی‌گیرد. در حقیقت گره‌های سبز رنگ (برای مقادیر صحیح) همیشه در بالای گره‌های قرمز رنگ (برای مقادیر نادرست) قرار خواهند داشت.

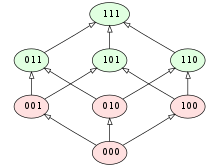
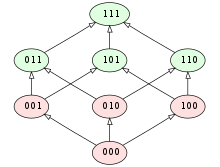
در مقابل نموداری که در تصویر ۶ دیده می‌شود، بیانگر یک نمودار غیریکنوا است. همانطور که مشخص است بعضی از گره‌ها با مقدار ۱ ( به رنگ سبز) در زیر گره‌های با مقدار نادرست (به رنگ قرمز) قرار گرفته‌اند.

فیلم آموزش ساختمان گسسته – مرور و حل تست های کنکور کارشناسی ارشد در فرادرس

کلیک کنید

نکته: «نمودار هسه» (Hasse Diagram) همان نقش نمودارهای ون را در فضای سه مقداری ایفا می‌کند. در اینجا هر یک از مجموعه‌ها نیز شامل سه مقدار یا سه مولفه هستند.

توابع یکنوای بولی را می‌توان دقیقا به صورت عملگرهای دو دویی مانند عملگر «و» (AND)، «یا» (OR) در نظر گرفت. برای مثال محاسبه گزاره منطقی «حداقل دو تا از گزاره‌های a,b,c صحیح باشند»، یک تابع یکنوا روی a,b,c است. زیرا می‌توان کل عبارت را به صورت گره‌هایی به شکل زیر از ترکیب گزاره‌هایی برحسب AND و OR نوشت:

$$ \large [(a \text{  AND  } b) \text{  OR  } (a \text{  AND  } c) \text{  OR  } (b \text{  AND  } c) ]$$

نکته: تعداد چنین توابعی با $$n$$ متغیر را «عدد ددکیند» (Dedekind Number) برای $$n$$ تعریف کرده و در نظریه ترتیب به کار می‌برند.

خلاصه و جمع‌بندی

در این نوشتار به معرفی و بررسی خصوصیات «تابع یکنوا» (Monotone Function) پرداختیم. «صعودی» (Ascending) یا «نزولی» (Descending) بودن یکی از خصوصیات اصلی برای تابع یکنوا است. تعریف تابع یکنوا نیز اغلب بر تابع نزولی یا تابع صعودی، استوار است. همچنین در نظریه احتمال، خصوصیت مهم برای تابع احتمال تجمعی، یکنوا بودن آن است. همچنین توابع و تبدیلات یکنوا در آنالیز ریاضی و نظریه اندازه نقش مهمی ایفا می‌کنند.