کنترل فرآیندهای شیمیایی – به زبان ساده

در سالهای اخیر، نیازهایی که برای بهبود عملکرد نیروگاهها و تاسیسات شیمیایی مورد استفاده قرار میگیرند، با دشواریهای بسیاری همراه بودهاند. مباحث رقابتی، زیستمحیطی و ایمنی از عوامل مهم به شمار میآیند. در نتیجه این شرایط جدید، مشخصههای سختتری برای تاسیسات و کیفیت محصولات در نظر گرفته شدهاند. این پیچیدگیها سبب شده تا تاسیسات جدید با دشواری بیشتری برای عملیاتی شدن همراه باشند چراکه فرآیندهای مورد نیاز برای اجرا، با پیچیدگیهای جدیدتری روبرو هستند. با توجه به دشواریهایی که مطرح شد و حساسیت بیشتر برای بازده این تاسیسات، طبیعی است که مباحثی همچون کنترل فرآیندهای شیمیایی مورد توجه قرار گیرند.
در این آموزش قصد داریم تا به زبانی ساده، مباحث پایه و نظری در کنترل فرآیندهای شیمیایی را مورد بررسی قرار دهیم. البته لازم به ذکر است که بدون سیستمهای کنترلی کامپیوتری، کنترل تاسیسات امکانپذیر نیست و به همین جهت، مهندسین شیمی باید از لحاظ نظری و عملی با مفهوم کنترل فرآیندهای شیمیایی آشنا باشند.
اهداف اصلی کنترل فرآیندهای شیمیایی انجام فرآیند در شرایط عملیاتی مورد نظر برای حصول نتیجه مناسب با در نظر گرفتن شرایط اقتصادی، ایمنی، زیستمحیطی و ... است. در مقیاس بزرگتر، تاسیسات فرآیندی همچون پالایشگاههای نفتی یا تاسیسات اتیلن، دارای متغیرهای کنترلی بسیاری همچون درصد ترکیب، دما و فشار هستند که باید کنترل شوند. از متغیرهای فرآیندی به خصوص دبی جریان برای کنترل فرآیندهای شیمیایی بهره میگیرند. «سیستمهای کنترل پسخور» (Feedback Control Systems)، مقادیر بدست آمده را با مقادیر مطلوب مقایسه میکنند و متغیرها را به شکل مناسب تنظیم میکنند.
مقدمهای بر مسائل کنترل فرآیندهای شیمیایی
اساس کنترل فرآیندهای شیمیایی در حقیقت، فهم واژه «فرآیند» (Process) است. به همین منظور باید به این سوال پاسخ بدهیم که فرآیند چیست؟ تعریفی کوتاه از فرآیند را میتوان به صورت زیر ارائه داد:
تعریف فرآیند در کنترل فرآیندهای شیمیایی عبارتست از تبدیل خوراک به فرآورده از طریق عملیات شیمیایی و فیزیکی. در عمل، عبارت فرآیند در هر دو مورد عملیات و تجهیزات فرآیندی مورد استفاده قرار میگیرد. سه دسته اصلی در فرآیندها وجود دارند که عبارتند از «پیوسته» (Continuous)، «دستهای» (Batch) یا ناپیوسته و «نیمهدستهای» (Semibatch). در ادامه قصد داریم به توضیح مختصری در رابطه با فرآیندهای پیوسته در کنترل فرآیندهای شیمیایی بپردازیم.
فرآیندهای پیوسته
در تصویر زیر، چهار فرآیند پیوسته به صورت شماتیک نشان داده شده که این چهار فرآیند به صورت زیر است:
- مبدل حرارتی لولهای: در این مبدل، مایع درون لوله توسط آب در بخش پوسته مبدل، خنک میشود. به طور معمول، دمای خروجی در این فرآیند به وسیله تغییر دبی جریان آب خنککننده، کنترل میشود.
- راکتور همزندار پیوسته: اگر واکنش به شدت گرماده باشد، باید دمای راکتور را به کمک دبی جریان خنککننده در یک محفظه کنترل کنیم.
- کوره کراکینگ حرارتی: در این فرآیند، نفت خام به برشهای سبکتر شکسته میشود. دمای کوره و مقدار هوای اضافی را به کمک دبی جریان سوخت و نسبت سوخت به هوا کنترل میشود.
- واحد دیالیز کلیه: از دستگاه دیالیز برای تصفیه خون بهره میگیرند. دبی جریان خون توسط یک پمپ و شرایط محیط همچون دما کنترل میشود.
برای هرکدام از چهار مثال بالا، مسائل کنترل فرآیندهای شیمیایی به کمک چهار نوع متغیر فرآیندی، مشخصهسازی میشوند:
- متغیرهای کنترل شده: متغیرهای فرآیند که کنترل شدهاند را با نام «متغیرهای کنترل شده» (Controlled Variables) یا متغیرهای کنترلی میشناسند. مقدار مطلوب یک متغیر کنترل شده، «نقطه تنظیم» (Set Point) یا نقطه میزان نام دارد.
- متغیر کنترل کننده یا تنظیمی: متغیرهای فرآیند که میتوان آنها را برای نگهداشتن متغیرهای کنترلی در نزدیکی نقطه میزان، تنظیم کرد با نام «متغیر تنظیمی» (Manipulated Variable) شناخته میشوند.
- متغیر آشوبی: متغیرهایی که بر متغیرهای کنترلشده تاثیر میگذارند اما قابلیت تنظیم ندارند، موسوم به «متغیر آشوبی» (Disturbance Variable) هستند. آشوب (اغتشاش) به طور کلی با تغییرات محیط عملیاتی فرآیند همچون شرایط دمایی و خوراک رابطه دارد. برخی از این متغیرها را به طور پیوسته میتوان اندازهگیری کرد اما برخی دیگر همچون ترکیب نفت خام این قابلیت را ندارند.
تعیین این سه متغیر، گامی مهم در توسعه یک سیستم در کنترل فرآیندهای شیمیایی به شمار میآید. انتخاب این متغیرها باید بر اساس دانش فرآیند، تجربه و اهداف کنترل فرآیندهای شیمیایی باشد.
فرآیند همزن
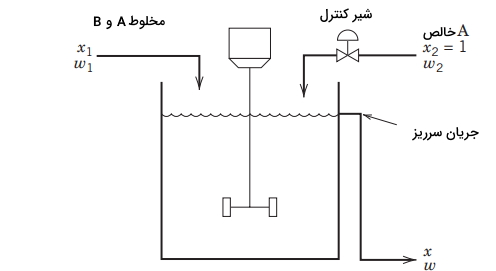
یک فرآیند ساده موسوم به «فرآیند همزن» (Blending Process) را جهت معرفی ابتدایی طراحی سیستمهای کنترل در کنترل فرآیندهای شیمیایی بکار میبرند. فرآیند مخلوط کردن یا همزدن در بسیاری از صنایع بمنظور دستیابی به محصول مورد نظر مشتری مورد استفاده قرار میگیرد. در تصویر زیر، یک مخلوطکننده همزندار پیوسته را مشاهده میکنید. هدف کنترل فرآیندهای شیمیایی در این مساله آن است که دو جریان ورودی با یکدیگر مخلوط شوند تا جریان خروجی با ترکیب مطلوب بدست آید. جریان اول شامل دو ماده شیمیایی A و B است. فرض میکنیم که دبی جرمی این جریان ثابت و کسر جرمی A یعنی با زمان متغیر باشد. جریان دوم، شامل ماده خالص A و بنابراین در این جریان، خواهد بود.
دبی جرمی جریان دوم را میتوان به کمک یک شیر کنترل، تنظیم کرد. کسر جرمی A در جریان خروجی را با و مقدار مطلوب (نقطه تنظیم) را نشان میدهیم. بنابراین، برای این مساله، متغیر کنترلی ، متغیر تنظیمی و متغیر آشوبی خواهد بود. در ادامه، دو سوال مطرح میشود:
سوال اول: اگر متغیر اسمی ، باشد، چه مقدار جریان اسمی نیاز داریم تا به غلظت مطلوب برسیم.
برای پاسخ به این سوال، یک حالت موازنه جرم «پایا» (Steady-state) را در نظر میگیریم.
موازنه جرم کلی:
رابطه (1):
موازنه جرم برای جزء A:
رابطه (2):
خطی که بالای نمادها نوشته شده بیانگر مقادیر در حالت پایا است. بر اساس گفتههای مساله، و خواهد بود. با حل رابطه ۱ برای و جایگذاری مقادیر آن در رابطه ۲ و بازآرایی مجدد، به رابطه زیر میرسیم:
رابطه (3):
رابطه بالا، رابطه مربوط به طراحی یک سیستم همزن است. اگر فرضهای ما صحیح باشند و همچنین اگر ، در نتیجه، مقدار ، ما را به نتیجه مطلوب میرساند. اما اگر شرایط تغییر کنند، چه اتفاقی خواهد افتااد؟ در اینجا سوال دوم مطرح میشود.
سوال دوم: فرض کنید غلظت ورودی با زمان تغییر کند. چطور اطمینان حاصل کنیم که ترکیب خروجی به مقدار مطلوب نزدیک خواهد شد؟
در این مثال، فرض کنید که تا یک مقدار ثابت بزرگتر از مقدار اسمی خود یعنی ، افزایش پیدا کند. واضح است که ترکیب خروجی نیز به دلیل این افزایش، افزایش مییابد. در نتیجه، در این شرایط پایدار (پایا) جدید، خواهد بود. در ادامه، استراتژیهای مختلف را برای کاهش تاثیر آشوب روی در نظر خواهیم گرفت.
روش اول
را اندازهگیری و را تنظیم کنید. به طور مثال، اگر بسیار زیاد باشد، بنابراین، باید کاهش بیابد. اگر بسیار کم باشد، باید افزایش پیدا کند. این روش کنترلی میتواند توسط یک اپراتور (کنترل دستی) به انجام برسد اما به لحاظ اقتصادی بهتر است که چنین روشی به طور خودکار (کنترل اتوماتیک) اجرا شود. روش اول را میتوان به صورت یک الگوریتم ساده کنترل یا قانون کنترل اجرا کرد.
رابطه (4):
در رابطه بالا، یک ثابت موسوم به «بهره کنترلکننده» (Controller Gain) است. در این رابطه، نشان داده شده است که عبارات و با زمان تغییر میکنند. رابطه ۴، مثالی از یک «کنترل نسبی» (Proportional Control) است چراکه تغییر در دبی جریان ، متناسب با انحراف از نقطه تنظیم است. در نتیجه، انحراف زیاد از نقطه تنظیم، «عمل اصلاحی» (Corrective Action) زیادی را تولید میکند در صورتیکه انحراف کم، عمل اصلاحی کمی را به همراه خواهد داشت. توجه داشته باشید که در این رابطه، باید مقداری مثبت داشته باشد زیرا باید به هنگام کاهش ، افزایش پیدا کند و برعکس. البته در برخی مسائل کنترل فرآیندهای شیمیایی این مقدار، عددی منفی را نیز اختیار میکند.
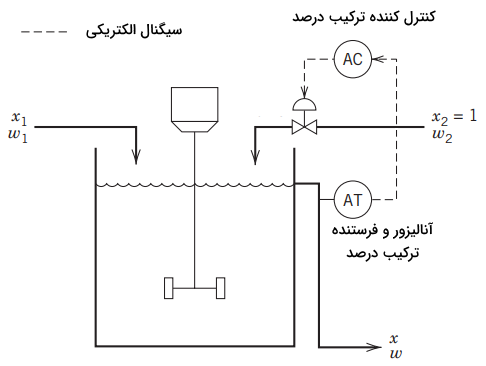
دیاگرامی از روش اول را در تصویر زیر مشاهده میکنید. غلظت خروجی اندازهگیری و به صورت یک سیگنال الکتریکی به کنترلکننده منتقل میشود. کنترلکننده پس انجام قانون کنترل مطرح شده در بالا، سیگنال الکتریکی مناسب را به شیر کنترل ارسال خواهد کرد که بر اساس آن، شیر کنترل باز یا بسته خواهد شد.
روش دوم
در روش دوم، مقدار اندازهگیری و بر مبنای آن تنظیم میشود. بنابراین، اگر ، مقدار را کاهش خواهیم داد. قانون کنترلی بر مبنای رابطه ۳ نیز بدست میآید که در آن، به جای از و بجای از استفاده شده است:
رابطه (5):
روش سوم
روش سوم، ترکیبی از روش اول و دوم است به گونهای که مقادیر و اندازهگیری و بر مبنای آن، تنظیم خواهد شد.
روش چهارم
در روش چهارم، از یک مخزن بزرگتر بهره میگیریم. با استفاده از مخزن بزرگتر، نوسانات به دلیل حجم بیشتر مایع، کاهش پیدا میکنند. البته توجه داشته باشید که این روش، هزینههای بیشتری را به همراه خواهد داشت.

دستهبندی استراتژیها در کنترل فرآیندهای شیمیایی
در ادامه قصد داریم تا در خصوص روشهای مطرح شده در بخش قبل صحبت و نقاط قوت و ضعف آنها را بررسی کنیم. روش اول، مثالی از «استراتژی کنترل پسخور» (Feedback Control Strategy) بود. ویژگی اصلی در کنترل پسخور (فیدبک)، آن است که متغیر کنترلی، اندازهگیری میشود و از مقدار آن برای تغییر متغیر تنظیمی بهره میگیرند. در این روش، متغیر آشوبی اندازهگیری نخواهد شد.
این نکته بسیار مهم است که بین فیدبک مثبت و منفی، تفاوت قائل شویم. در متون مهندسی، فیدبک منفی به شرایطی اطلاق میشود که عمل اصلاحی کنترلکننده، متغیر کنترلی را به سمت نقطه تنظیم هدایت کند. در مقابل، زمانی که فیدبک مثبت داشته باشیم، کنترل کننده، متغییر کنترلی را از نقطه تنظیم دور میکند. به طور مثال در خصوص همزن، زمانی فیدبک مثبت خواهیم داشت که زیرا در این حالت، با افزایش ، افزایش خواهد یافت. بنابراین، به طور واضح مشخص است که در کنترل فرآیندهای شیمیایی باید شرایط به گونهای باشد که سیستم با فیدبک منفی داشته باشیم.
از نقاط قوت کنترل فیدبک آن است که عمل اصلاحی، مستقل از منبع آشوب عمل میکند. توانایی این مدل در کنترل آشوبها با منشا ناشناخته از جمله دلایلی است که از این استراتژی به عنوان یک روش اصلی استفاده میشود. نقطه قوت دیگر این روش، آن است که کنترل فیدبک، حساسیت متغیر کنترلی را نسبت به آشوبهای اندازهگیری نشده و تغییرات فرآیند کاهش میدهد. با این وجود، این روش یک محدودیت اساسی دارد: هیچ عمل اصلاحی صورت نمیگیرد مگر آنکه آشوبی در سیستم و به دنبال آن در فرآیند رخ دهد و این مورد زمانی انجام میگیرد که متغیر کنترلی از نقطه تنظیم انحراف پیدا کند.
روش دوم، نمونهای از استراتژی «کنترل پیشخور» (Feedforward Control) بود. ویژگی این روش در آن است که متغیر آشوبی اندازهگیری میشود اما این کار برای متغیر کنترلی انجام نخواهد شد. نقطه قوت این روش، انجام عمل اصلاحی، قبل از انحراف متغیر کنترلی از نقطه تنظیم است. در یک شرایط ایدهآل، عمل اصلاحی، اثر آشوب را خنثی میکند و در نتیجه، متغیر کنترلی، از آشوب تاثیر نمیگیرد. با وجود اینکه رسیدن به این حالت امکانپذیر نیست اما کنترل پیشخور به طور مشخصی، اثر آشوب اندازهگیری شده را کاهش میدهد. روش کنترل پیشخور، دو نقطه ضعف اساسی دارد:
- متغیر آشوبی باید اندازهگیری (سنجش) یا به طور دقیق تخمین زده شود.
- هیچ عمل اصلاحی برای متغیر آشوبی در صورت عدم سنجش صورت نمیگیرد.

در این روش، به یک مدل فرآیندی نیاز داریم. به طور مثال در خصوص مثال همزن و استراتژی دوم، هیچ عمل اصلاحی برای صورت نمیگیرد. به طور کلی، این مشکل را با سنجش هر دو مقدار و و تنظیم حل میکنیم. با این وجود، در صنعت، اینکه بخواهیم تمامی متغیرهای آشوبی را بسنجیم، به لحاظ اقتصادی صرفه چندانی ندارد. روش عملی در مواجهه با این مسائل، ترکیب سیستم کنترل پیشخور-پسخور است که در آن، کنترل پسخور، عمل اصلاحی را برای متغیر آشوبی انجام میدهد و کنترل پیشخور، قبل از تغییرات متغیر کنترلی، نسبت به متغیر آشوبی وارد عمل میشود.
بنابراین، در صنایع، کنترل پیشخور را در ترکیب با کنترل پسخور بکار میگیرند. این روش، در استراتژی سوم مطرح شد زیرا در آن، و اندازهگیری شدند. در نهایت، روش چهارم به طور کلی، طراحی سیستم کنترل را تغییر میدهد و به طور حقیقی، یک استراتژی کنترلی به شمار نمیآید.
ستون تقطیر، نمونهای پیچیدهتر در کنترل فرآیندهای شیمیایی
سیستم همزن در بخش قبل، مثالی ساده بود چراکه تنها یک متغیر کنترلی و یک متغیر تنظیمی داشتیم. در بسیاری از کاربردهای عملی، چندین متغیر کنترلی و تنظیمی داریم. به عنوان نمونه، یک ستون تقطیر را در تصویر زیر در نظر میگیریم. در این ستون، ۵ متغیر کنترلی و ۵ متغیر تنظیمی وجود دارد. متغیرهای کنترلی در زیر آورده شدهاند:
- درصد ترکیب فرآوردهها: و
- فشار ستون:
- سطح مایع در محفظه بازگشتی و پایین ستون که به ترتیب با و نشان داده شدهاند.
پنج متغیر تنظیمی نیز به صورت زیر تعریف میشوند:
- دبی جریانی فرآورده: و
- جریان بازگشتی:
- گرمای پیشگرمکن (ریبویلر) و کندانسور که به ترتیب با و نشان داده میشوند.
مقادیر گرما به کمک شیرهای کنترلی تنظیم میشوند. فرض بر این است که جریان خوراک از یک واحد «بالادستی» (Upstream) تامین شود. در نتیجه، دبی جریانی خوراک قابل تنظیم نخواهد بود اما میتوان مقدار آنرا اندازهگیری کرد و در سیستم کنترل پیشخور مورد استفاده قرار داد.
این ستون تقطیر به طور معمول، از شش حلقه کنترل پسخور تشکیل شده است. هر حلقه کنترل از یک متغیر تنظیمی برای کنترل یک متغیر کنترلی بهره میگیرد. برای سیستمهای کنترلی که این نوع حلقههای کنترلی معمول، کاربرد نداشته باشند، از «کنترل چندمتغیره» (Multivariable Control) استفاده میشود. در این روش، هر متغیر تنظیمی بر اساس حداقل دو متغیر کنترلی تنظیم خواهد شد. این تنظیمات بر اساس مدل دینامیکی فرآیند و تاثیر متغیرهای تنظیمی به انجام میرسند. به همین دلیل، عملکرد سیستمهای کنترل چندمتغیره، به شدت به دقت مدل فرآیند بستگی دارد.
نگاهی به مدل دینامیکی در فرآیند همزن
در ابتدای این آموزش، یک مدل پایدار برای مخزن همزندار بر اساس موازنه جرم ارائه دادیم. در ادامه قصد داریم یک مدل «غیرپایا» (Unsteady-State) را بررسی کنیم که به ما در آنالیز موقیعتهای معمول، کمک بیشتری میکند. در چنین شرایطی، متغیرهای فرآیند با زمان متغیر هستند و عبارات تجمعی را باید در مدل لحاظ کنیم. به عنوان نمونه، یک سیستم همزندار همدما را مطابق تصویر زیر در نظر میگیریم. این تصویر، شکل کلیتری از تصویر قبل را برای سیستم همزندار نشان میدهد زیرا جریان سرریز در این سیستم حذف شده است و جریان ۲ نیز، خالص نیست یا به عبارت دیگر خواهد بود.
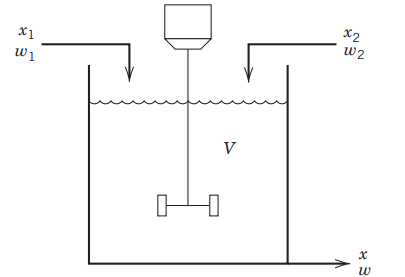
در این حالت، حجم مخزن (V) با زمان تغییر خواهد کرد و دبی جریان خروجی لزوما با مجموع دبیهای ورودی برابر نیست. در نتیجه، موازنه جرم برای حالت ناپایدار در یک سیستم مانند تصویر بالا به شکل زیر خواهد بود:
رابطه (۶): نرخ جرم خروجی - نرخ جرم ورودی = نرخ تجمع جرم در مخزن
جرم مایع موجود در مخزن را میتوان به صورت حاصلضرب حجم در چگالی بیان کرد. در نتیجه، نرخ تجمع جرم و رابطه ۶ را میتوان به شکل ساده زیر نوشت:
رابطه (7):
موازنه جرم حالت ناپایدار برای جزء A نیز با روشی مشابه بدست میآید. فرض میکنیم که اختلاط در مخزن به خوبی انجام شود. این فرض، مستلزم وجود دو شرط است: هیچ گرادیانی از غلظت در محتوای مخزن وجود نداشته و ترکیب اجزا در خروجی با ترکیب اجزا در مخزن، یکی باشد. فرض اختلاط کامل در مایعات با ویسکوزیته پایین قابل دسترس است چراکه تلاطم مناسبی در این مایعات خواهیم داشت. در مقابل، مایعات با ویسکوزیته بالا همچون پلیمرها یا مواد مذاب، چنین شرایطی را بدست نمیدهند. بنابراین، رابطه موازنه جرم برای جزء A با فرض اختلاط کامل، به صورت زیر خواهد بود که در آن، نشاندهنده کسر جرمی A است.
رابطه (۸):
روابط ۷ و ۸ را میتوان سادهتر کرد تا به کمک آنها، بتوان شبیهسازی کامپیوتری را انجام داد. در این روش، فرض دیگری مطرح میشود و آن، ثابت بودن چگالی مایع است. این فرض، فرض صحیحی به شمار میآید چراکه در بیشتر موارد، چگالی، وابستگی کمی به ترکیب دارد. اگر چگالی ثابت باشد، روابط ۷ و ۸ به شکل زیر تبدیل خواهند شد:
رابطه (۹):
رابطه (10):
به کمک قاعده زنجیرهای مشتق، عبارت تجمع را به شکل زیر خواهیم نوشت:
رابطه (۱۱):
با جایگذاری رابطه ۱۱ در 10، به رابطه زیر میرسیم:
رابطه (12):
با جایگذاری رابطه ۹ در رابطه ۱۲ خواهیم داشت:
رابطه (۱۳):
بعد از سادهسازی روابط و بازآرایی آنها به دو رابطه زیر موسوم به مدل «فضای حالت» (State-Space) خواهیم رسید.
رابطه (۱۴):
رابطه (۱۵):
مدل دینامیک در روابط 14 و 15، شکلی کلی دارند و بر پایه دو فرض بنا شدهاند: «اختلاط کامل» (Perfect Mixing) و چگالی ثابت. در برخی شرایط ویژه، حجم مایع نیز ثابت و بنابراین رابطه برقرار خواهد بود و دبی جریان خروجی با مجموع دبیهای جریان ورودی، یعنی تعریف میشود. چنین شرایطی، زمانی اتفاق میافتند که:
- یک بخش سرریز داشته باشیم.
- مخزن به صورت بسته و به طور کامل پر شده باشد.
- کنترل کننده سطح مایع، با تنظیم دبی جریان، را ثابت نگه دارد.
دو مدل دینامیکی که در روابط ۱۴ و ۱۵ بیان شد را میتوانیم با روشهای تحلیلی و عددی بررسی کنیم. بمنظور بدست آوردن جواب معادله دیفرانسیل معمولی (ODE)، باید ترکیب ورودی ( و ) و دبیهای جریان (، و ) را به صورت تابعی از زمان تعیین کنیم. بعد از مشخص شدن شرایط اولیه برای متغیرهای مستقل و ، پاسخ گذرای و تعیین میشوند. بدست آوردن یک رابطه تحلیلی برای زمانی که V ثابت باشد را در مثال زیر، بررسی خواهیم کرد.
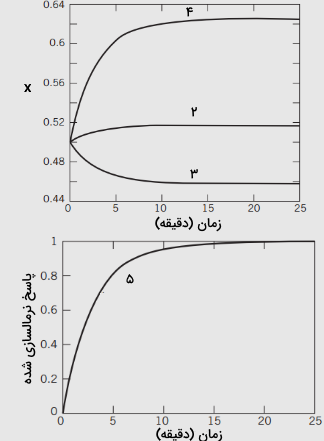
مثال برای بدست آوردن رابطه تحلیلی با حجم ثابت
یک همزن با «هلدآپ» (Holdup) مایع ۲ متر مکعب بمنظور مخلوط کردن دو جریان با چگالی بکار گرفته میشود. به هنگام اختلاط، تغییر چگالی نخواهیم داشت.
- فرض کنید این فرآیند برای مدت زمانی طولانی با دبی جریانی و ، ادامه پیدا میکند. کسر جرمی خوراک به صورت و تعریف میشود. مقدار را در حالت پایدار محاسبه کنید.
- فرض کنید که به طور ناگهانی از به تغییر پیدا کند و در این مقدار، ثابت بماند. رابطهای برای پیدا و آنرا رسم کنید.
- فرآیند ۲ را اینبار برای تغییر از به انجام دهید.
- محاسبات ۳ را برای حالتی که به طور ناگهانی از 0/4 به 0/6 تغییر کند را علاوه بر تغییرات انجام دهید.
- برای هریک از بخشهای ۱ تا ۴، پاسخ نرمالسازی شده را رسم کنید:
در رابطه بالا، مقدار اولیه حالت پایدار برای است و ، مقدار نهایی را مشخص میکند که برای هر بخش، با دیگری متفاوت است.

حل
1. شرایط اولیه حالت پایدار را به صورت و نشان میدهیم. بنابراین خواهیم داشت:
2. معادله موازنه اجزا را برای حجم و چگالی ثابت، به صورت زیر بازنویسی میکنیم:
رابطه (16):
در رابطه بالا داریم:
برای بخشهای ۲ تا ۴، مقدار برابر با ۳ خواهد بود و سمت راست رابطه (16) برای این مثال، عددی ثابت است، بنابراین، رابطه (16) را میتوانیم به شکل زیر بنویسیم:
رابطه (17):
که در این رابطه:
رابطه (18):
برای حل رابطه 17 میتوانیم از معادله زیر کمک بگیریم:
رابطه (۱۹):
برای حل سوال ۲ خواهیم داشت:
با جایگذاری مقدار در رابطه 19، به راه حل مناسب برای تغییر پلهای در میرسیم:
رابطه (20):
3. برای تغییر پلهای در خواهیم داشت:
در نتیجه، برای حل به معادله زیر خواهیم رسید:
رابطه (21):
4. به طور مشابه، برای تغییرات همزمان و ، مقدار برابر با 0/625 خواهد بود و معادله جواب متناظر با این عدد به شکل زیر است:
رابطه (22):
جواب معادلات 19-22، به صورت پاسخ نرمالسازی شده زیر نیز بدست میآید:
رابطه (23):
نمودار پاسخ برای سولات ۲-۵ در تصویر زیر نشان داده شده است:
تبدیلات لاپلاس و توابع تبدیل
تا اینجا بیشتر در خصوص مدلهای دینامیکی و معادله دیفرانسیل معمولی (ODE)، صحبت کردیم. البته بحث کنترل فرآیندهای شیمیایی و به طور کلی کنترل فرآیند، با تبدیلات لاپلاس و «توابع تبدیل» (Transfer Functions) معنا پیدا میکنند. در ادامه قصد داریم با زبانی ساده، مدلی جایگزین بر اساس تبدیلات لاپلاس یعنی همان مدل تابع تبدیل را ارائه کنیم. از هر دو مدل میتون برای تعیین رفتار دینامیکی در فرآيند به هنگام تغییر متغیرهای ورودی بهره گرفت. علاوه بر این، توابع تبدیل، نقش مهمی را در طراحی و آنالیز سیستمها در کنترل فرآیندهای شیمیایی ایفا میکنند.
تابع تبدیل
تصویر زیر، یک مدل دینامیکی ساده را با یک متغیر ورودی u و یک متغیر خروجی y نشان میدهد. این مدل زمانی که u را به y مرتبط میکند، از نوع ODE به شمار میآید. برای یک ODE خطی، مدلی معادل ، موسوم به مدل تابع تبدیل بر اساس تبدیلات لاپلاس وجود دارد.
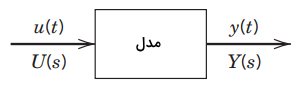
طبق تعریف، تابع تبدیل بین u و y به صورت زیر است:
رابطه (24):
در رابطه بالا، و خواهد بود. تابع تبدیل در رابطه ۲۴ بر اساس متغیرهای فیزیکی y و u تعریف شده است. با این وجود، به طور معمول برای راحتی کار، توابع تبدیل را بر اساس متغیرهای انحرافی تعریف میکنند. به طور مثال، متغیرهای انحرافی برای y و u به صورت زیر تعریف میشوند.
رابطه (25):
در این رابطه، و ، متغیرهای انحرافی و و ، مقادیر اسمی حالت پایدار هستند. مثال زیر، نحوه بدست آمدن تابع تبدیل بر اساس مدل ODE را نشان میدهد.
مثال بدست آوردن تابع تبدیل بر اساس ODE
مدل زیر را برای مخزن در نظر بگیرید:

معادله دیفرانسیل خطی مرتبه اول مدل بالا به شکل زیر خواهد بود:
رابطه (26):
در رابطه بالا، h سطح مایع، دبی جریان ورودی و A و نیز اعداد ثابت هستند.
- یک مدل تابع تبدیل بین h و بر اساس متغیرهای انحرافی بدست آورید.
- از مدل تابع تبدیل برای تعیین پاسخ بر اساس تغییر پلهای با مقدار در استفاده کنید.
پاسخ 1: در این مثال، دو متغیر انحرافی به صورت زیر تعریف میشوند:
رابطه (27):
متغیرهای انحرافی را میتوان با کم کردن مدل حالت پایدار دینامیکی از خود مدل بدست آورد. مدل حالت پایدار رابطه 26، به شکل زیر است:
رابطه (28):
با کمک کردن رابطه ۲۸ از ۲۶، به رابطه زیر میرسیم:
رابطه (29):
با توجه به ثابت بودن ، به کمک رابطه ۲۷، رابطه زیر بدست میآید:
رابطه (30):
با جایگذاری رابطه 30 در سمت چپ رابطه 29 و سپس جایگذاری رابطه 27، مدل دینامیکی زیر بر اساس متغیرهای انحرافی، بدست میآید:
رابطه (31):
در ادامه، فرض میکنیم که مخزن مایع در ابتدا در حالت پایدار اسمی خود قرار دارد. بنابراین، و با توجه به رابطه 27 خواهیم داشت:
اگر از دو طرف رابطه 31، تبدیل لاپلاس بگیریم خواهیم داشت:
رابطه (32):
با بازآرایی این رابطه، به تابع تبدیل مطلوب خواهیم رسید:
رابطه (33):
پاسخ 2: برای بدست آوردن پاسخ پلهای، در ابتدا رابطه 33 را به شکل زیر بازآرایی میکنیم:
رابطه (34):
برای تغییر پلهای با بزرگی در ، و . با جایگذاری این عبارات در رابطه ۳۴ خواهیم داشت:
رابطه (35):
به کمک فرمولهای تبدیل لاپلاس، اگر از رابطه ۳۵، لاپلاس معکوس بگیریم، پاسخ سطح مایع بدست خواهد آمد:
رابطه (36):
در نهایت، با جایگذاری رابطه ۲۷ و بازآرایی آن، به نتیجه مطلوب خواهیم رسید:
رابطه (37):

فیلم آموزش کنترل فرآیندها (مرور و حل تست کنکور ارشد)
همانطور که در طول این آموزش مشاهده کردید، کنترل فرآیندهای شیمیایی از جمله مباحثی است که فهم آن به صورت نظری، برای درک هرچه بیشتر کاربرد عملی و پیادهسازی مدلها بسیار اهمیت دارد. از اینرو، مسائل کنترل فرآیندهای شیمیایی در آزمونهای مهم همچون امتحانات پایان ترم و کنکور کارشناسی ارشد، اهمیت بسیار زیادی دارند و دانشجویان برای درک مباحث مختلف کنترل فرآیندهای شیمیایی با دشواریهایی روبرو هستند. به همین جهت، فرادرس اقدام به انتشار آموزش ویدیویی تحت عنوان «آموزش کنترل فرآیندها (مرور و حل تست کنکور ارشد)» در قالب یک آموزش ۹ ساعته کرده که از این لینک قابل دسترس است.
البته این آموزش تنها محدود به حل سوالات نیست بلکه در پنج درس، به بررسی مفاهیم مرتبط با کنترل فرآیندهای شیمیایی پرداخته میشود. درس اول، به طور کامل، تبدیلات لاپلاس و تمامی فرمولهای مورد نیاز، تدریس خواهند شد و در انتهای مبحث نیز، حل معادلات دیفرانسیل به کمک تبدیلات لاپلاس را فرا میگیرید. درس دوم به تحلیل فرآیندهای کنترلی میپردازد. در این درس، تابع انتقال سیستمهای درجه اول و دوم و همچنین پاسخ این سیستمها به ورودیهای مختلف بررسی میشود.
در درس سوم، انواع کنترلر و نحوه یافتن تابع انتقال در سیستمهای مدار بسته و پیچیده تدریس خواهد شد و افت کنترل و چگونگی انتخاب کنترلر مناسب در کنترل فرآیندهای شیمیایی مورد بررسی قرار میگیرد. آنچه در تمامی مسائل کنترل فرآیندهای شیمیایی دنبال میشود، مبحث پایداری است که در درس چهارم به آن پرداخته خواهد شد. آزمون روت و همچنین مباحث مربوط به مکان هندسی ریشهها را در این درس میآموزید. در درس پنجم، پاسخ فرکانسی، «دیاگرام بود» (Bode Diagram) و پایداری آنها به کمک روش زیگلر-نیکولز بررسی میشود. در انتهای آموزش کنترل فرآیندهای شیمیایی نیز سوالات منحنیهای نایکوئیست، حاشیه بهره و حاشیه فاز بررسی خواهند شد.
اگر این مطلب برای شما مفید بوده است، آموزشها و مطالب زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای مهندسی کنترل
- مجموعه آموزشهای مهندسی شیمی
- آموزش شبیهسازی با سیمیولینک Simulink
- نمایش سیستم های کنترل — مجموعه مقالات جامع مجله فرادرس
- بلوک دیاگرام در مهندسی کنترل — به زبان ساده
^^