مشتقگیری از انتگرال عملیاتی در حسابان است که برای محاسبه برخی انتگرالها استفاده میشود. مشتق انتگرال این امکان را میدهد تا مرتبه انتگرالگیری و مشتقگیری را تغییر دهیم.
در سادهترین شکل این کار، به نام «قانون انتگرال لایبنیتس» (Leibniz Integral Rule)، مشتق از انتگرال منجر به معادله زیر میشود:
d d x ∫ a b f ( x , t ) d t = ∫ a b ∂ ∂ x f ( x , t ) d t . \large \frac { d } { d x } \int _ { a } ^ { b } f ( x , t ) \, d t = \int _ { a } ^ { b } \frac { \partial } { \partial x } f ( x , t ) \, d t . d x d ∫ a b f ( x , t ) d t = ∫ a b ∂ x ∂ f ( x , t ) d t .
بسیاری از انتگرالها که حل آنها دشوار است یا به روشهای پیچیدهای برای حل نیاز دارند، با این روش قابل حل هستند.
فرم کلی مشتق انتگرال
عمومیترین فرم مشتق انتگرال اینگونه است: اگر f ( x , t ) f ( x , t ) f ( x , t ) تابع پیوسته و مشتقپذیر پیوسته باشد (یعنی مشتقات جزئی آن وجود دارند و خود پیوستهاند) و حدود انتگرالگیری a ( x ) a ( x ) a ( x ) b ( x ) b ( x ) b ( x ) x x x
d d x ∫ a ( x ) b ( x ) f ( x , t ) d t = f ( x , b ( x ) ) ⋅ b ′ ( x ) − f ( x , a ( x ) ) ⋅ a ′ ( x ) + ∫ a ( x ) b ( x ) ∂ ∂ x f ( x , t ) d t . \large \frac { \mathrm { d } } { \mathrm { d } x } \int _ { a ( x ) } ^ { b ( x ) } f ( x , t ) \, \mathrm { d } t = f ( x , b ( x ) ) \cdot b' ( x ) - f ( x , a ( x ) ) \cdot a' ( x ) + \int _ { a ( x ) } ^ { b ( x ) } \frac { \partial } { \partial x } f ( x , t ) \, \mathrm { d } t . d x d ∫ a ( x ) b ( x ) f ( x , t ) d t = f ( x , b ( x )) ⋅ b ′ ( x ) − f ( x , a ( x )) ⋅ a ′ ( x ) + ∫ a ( x ) b ( x ) ∂ x ∂ f ( x , t ) d t .
برای مواردی که a ( x ) a ( x ) a ( x ) b ( x ) b ( x ) b ( x ) توابع ثابتی باشند، فرمول ساده زیر را خواهیم داشت:
d d x ∫ a b f ( x , t ) d t = ∫ a b ∂ ∂ x f ( x , t ) d t . \large \frac { \mathrm { d } } { \mathrm { d } x } \int _ { a } ^ { b } f ( x , t ) \,\mathrm { d } t = \int _ { a } ^ { b } \frac { \partial } { \partial x } f ( x , t ) \, \mathrm { d } t . d x d ∫ a b f ( x , t ) d t = ∫ a b ∂ x ∂ f ( x , t ) d t .
اثبات فرمول مشتق انتگرال
اثبات فرمول مشتق انتگرال را برای حالتی بیان میکنیم که حدود ثابت و برابر با a a a b b b x x x h > 0 h > 0 h > 0 x x x x + h x + h x + h [ x 0 , x 1 ] [x_0,x_1] [ x 0 , x 1 ]
∫ x x + h ∫ a b f x ( x , t ) d t d x = ∫ a b ∫ x x + h f x ( x , t ) d x d t = ∫ a b ( f ( x + h , t ) − f ( x , t ) ) d t = ∫ a b f ( x + h , t ) d t − ∫ a b f ( x , t ) d t \large \begin {align*} \int _ x ^ { x + h } \int _ a ^ b f _ x ( x , t ) \, d t \, d x & = \int_a^b \int_x^{x+h} f_x(x,t) \,dx \,dt \\& = \int_a^b \left(f(x+h,t)-f(x,t)\right) \,dt \\ &= \int_a^b f(x+h,t) \,dt - \int_a^b f(x,t) \,dt \end {align*} ∫ x x + h ∫ a b f x ( x , t ) d t d x = ∫ a b ∫ x x + h f x ( x , t ) d x d t = ∫ a b ( f ( x + h , t ) − f ( x , t ) ) d t = ∫ a b f ( x + h , t ) d t − ∫ a b f ( x , t ) d t
توجه کنید از آنجا که f x ( x , t ) f _x (x,t) f x ( x , t ) [ x 0 , x 1 ] ∗ [ a , b ] [x_0,x_1]*[a,b] [ x 0 , x 1 ] ∗ [ a , b ] d t d t d t d x dx d x
∫ a b f ( x + h , t ) d t − ∫ a b f ( x , t ) d t h = 1 h ∫ x x + h ∫ a b f x ( x , t ) d t d x = F ( x + h ) − F ( x ) h \large \begin{align*} \frac{\int_a^b f(x+h,t) \,dt - \int_a^b f(x,t) \,dt }{h} & = \frac{1}{h}\int_x^{x+h} \int_a^b f_x(x,t) \,dt \,dx \\ & = \frac{F(x+h)-F(x)}{h} \end {align*} h ∫ a b f ( x + h , t ) d t − ∫ a b f ( x , t ) d t = h 1 ∫ x x + h ∫ a b f x ( x , t ) d t d x = h F ( x + h ) − F ( x )
که در آن:
F ( u ) ≡ ∫ x 0 u ∫ a b f x ( x , t ) d t d x \large F(u) \equiv \int_{x_0}^{u} \int_a^b f_x(x,t) \,dt \,dx F ( u ) ≡ ∫ x 0 u ∫ a b f x ( x , t ) d t d x
F F F ∫ a b f x ( x , t ) d t \int_a^b f_x(x,t) \,dt ∫ a b f x ( x , t ) d t h h h
d d x ∫ a b f ( x , t ) \large \frac{d}{dx}\int_a^b f(x,t) d x d ∫ a b f ( x , t )
و برای سمت راست داریم:
F ′ ( u ) = ∫ a b f x ( x , t ) d t \large F'(u) = \int_a^b f_x(x,t) \,dt F ′ ( u ) = ∫ a b f x ( x , t ) d t
بنابراین، اثبات مورد نظر حاصل میشود:
d d x ∫ a b f ( x , t ) = ∫ a b f x ( x , t ) \large \frac{d}{dx}\int_a^b f(x,t) = \int_a^b f_x(x,t) d x d ∫ a b f ( x , t ) = ∫ a b f x ( x , t )
در صورت علاقه به یادگیری روشهای تعیین مشتق توابع مختلف، مطالعه مطلب «فرمولهای مشتق مهم + سوال با جواب و دانلود PDF » را به شما پیشنهاد میکنیم.
مثالهایی از مشتق انتگرال
به طور کلی، از مشتق انتگرال برای محاسبه انتگرالهایی استفاده میکنیم که متعلق به برخی از خانوادههای انتگرالهای پارامتری شده با یک متغیر حقیقی هستند. برای درک بهتر این موضوع، مثال زیر را در نظر بگیرید.
مثال اول مشتق انتگرال
انتگرال معین زیر را محاسبه کنید.
∫ 0 1 t 3 − 1 ln t d t . \large \int _ { 0 } ^ { 1 } \frac { t ^ { 3 } - 1 } { \ln t } \, d t . ∫ 0 1 ln t t 3 − 1 d t .
حل: به نظر میرسد که این انتگرال را نمیتوان با تکنیکهای استاندارد انتگرالگیری، مانند جزء به جزء ، تغییر متغیر و... حل کرد. بنابراین، آن را با مشتقگیری از انتگرال حل میکنیم.
اما برای استفاده از روش مشتق انتگرال باید چه تابعی را انتخاب کنیم؟ حضور ln t \ln t ln t
d d x t x = t x ln t , \large \frac { d } { d x } t ^ x = t ^ x \ln t , d x d t x = t x ln t ,
بنابراین، مشتق صورت نسبت به نما آن چیزی است که میخواهیم انجام دهیم.
بدین منظور، تابع زیر را تعریف میکنیم:
g ( x ) = ∫ 0 1 t x − 1 ln t d t . \large g ( x ) = \int _ { 0 } ^ { 1 } \frac { t ^ x - 1 } { \ln t } \, d t . g ( x ) = ∫ 0 1 ln t t x − 1 d t .
در این نمادگذاری، انتگرالی که باید محاسبه کنیم، g ( 3 ) g ( 3 ) g ( 3 ) g ( x ) g ( x ) g ( x ) x x x
طبق فرمول انتگرال لایبنیتس، عبارت زیر را محاسبه میکنیم:
g ′ ( x ) = ∫ 0 1 ∂ ∂ x t x − 1 ln t d t = ∫ 0 1 t x ln t ln t d t = t x + 1 x + 1 ∣ 0 1 = 1 x + 1 . \large g' ( x ) = \int _ { 0 } ^ { 1 } \frac { \partial } { \partial x } \frac { t ^ x - 1 } { \ln t } \, d t = \int _ { 0 } ^ { 1 } \frac { t ^ x \ln t } { \ln t } \, d t = \frac { t ^ { x + 1 } } { x + 1 } \Bigg \vert _ { 0 } ^ { 1 } = \frac { 1 } { x + 1 } . g ′ ( x ) = ∫ 0 1 ∂ x ∂ ln t t x − 1 d t = ∫ 0 1 ln t t x ln t d t = x + 1 t x + 1 0 1 = x + 1 1 .
در نتیجه، g ( x ) = ln ∣ x + 1 ∣ + C g ( x ) = \ln |x + 1 | + C g ( x ) = ln ∣ x + 1∣ + C C C C
برای مشخص کردن C C C g ( 0 ) = 0 g (0) = 0 g ( 0 ) = 0 0 = g ( 0 ) = ln 1 + C = C 0 = g ( 0 ) = \ln 1 + C = C 0 = g ( 0 ) = ln 1 + C = C g ( x ) = ln ∣ x + 1 ∣ g ( x ) = \ln |x + 1 | g ( x ) = ln ∣ x + 1∣ x x x g ( 3 ) = ln 4 = 2 ln 2 g ( 3 ) = \ln 4 = 2 \ln 2 g ( 3 ) = ln 4 = 2 ln 2
در مثال بالا، بخشی از انتگرالده با یک متغیر جایگزین شد و تابع حاصل با استفاده از مشتق انتگرال مورد مطالعه قرار گرفت. این مثال یک تصویر خوب از اصل حل مسئله است: اگر در یک مسئله خاص گیر کردهاید و به مشکل برخوردهاید، یک مسئله کلیتر را حل کنید.
مثال زیر کارایی فرم عمومی این روش را برای انتگرال گاوسی نشان میدهد.
مثال دوم مشتق انتگرال
انتگرال معین زیر را حل کنید.
∫ 0 ∞ e − x 2 / 2 d x . \large \int _ { 0 } ^ { \infty } e ^ { - x ^ 2 / 2 } \, d x . ∫ 0 ∞ e − x 2 /2 d x .
حل: تابع زیر را تعریف میکنیم:
g ( t ) = ( ∫ 0 t e − x 2 / 2 d x ) 2 . \large g ( t ) = \left ( \int _ { 0 } ^ { t } e ^ { - x ^ 2 / 2 } \, d x \right ) ^ 2 . g ( t ) = ( ∫ 0 t e − x 2 /2 d x ) 2 .
هدف محاسبه g ( ∞ ) g ( \infty ) g ( ∞ )
با مشتقگیری نسبت به t t t
g ′ ( t ) = 2 ⋅ ( ∫ 0 t e − x 2 / 2 d x ) ⋅ ( d d t ∫ 0 t e − x 2 / 2 d x ) = 2 e − t 2 / 2 ∫ 0 t e − x 2 / 2 d x = 2 ∫ 0 t e − ( t 2 + x 2 ) / 2 d x . \large \begin {align*} g' ( t ) & = 2 \cdot \left ( \int _ { 0 } ^ { t } e ^ { - x ^ 2 / 2 } \, d x \right ) \cdot \left ( \frac { d } { d t } \int _ { 0 } ^ { t } e ^ { - x ^ 2 / 2 } \, d x \right ) \\ & = 2 e ^ { - t ^ 2 / 2 } \int _ { 0 } ^ { t } e ^ { - x ^ 2 / 2 } \, d x = 2 \int _ { 0 } ^ { t } e ^ { - ( t ^ 2 + x ^ 2 ) / 2 } \, d x . \end {align*} g ′ ( t ) = 2 ⋅ ( ∫ 0 t e − x 2 /2 d x ) ⋅ ( d t d ∫ 0 t e − x 2 /2 d x ) = 2 e − t 2 /2 ∫ 0 t e − x 2 /2 d x = 2 ∫ 0 t e − ( t 2 + x 2 ) /2 d x .
از تغییر متغیر u = x / t u = x / t u = x / t
g ′ ( t ) = 2 ∫ 0 1 t e − ( 1 + u 2 ) t 2 / 2 d u . \large g' ( t ) = 2 \int _ { 0 } ^ { 1 } t e ^ { - ( 1 + u ^ 2 ) t ^ 2 / 2 } \, d u . g ′ ( t ) = 2 ∫ 0 1 t e − ( 1 + u 2 ) t 2 /2 d u .
اکنون انتگرالده یک پادمشتق به فرم بسته نسبت به t t t
g ′ ( t ) = − 2 ∫ 0 1 ∂ ∂ t e − ( 1 + u 2 ) t 2 / 2 1 + u 2 d u = − 2 d d t ∫ 0 1 e − ( 1 + u 2 ) t 2 / 2 1 + u 2 d u . \large g' ( t ) = - 2 \int _ { 0 } ^ { 1 } \frac { \partial }{ \partial t } \frac { e ^ { - ( 1 + u ^ 2 ) t ^ 2 / 2 } } { 1 + u ^ 2 } \, d u = - 2 \frac { d } { d t } \int _ { 0 } ^ { 1 } \frac { e ^ { - ( 1 + u ^ 2 ) t ^ 2 / 2 } } { 1 + u ^ 2 } \, d u . g ′ ( t ) = − 2 ∫ 0 1 ∂ t ∂ 1 + u 2 e − ( 1 + u 2 ) t 2 /2 d u = − 2 d t d ∫ 0 1 1 + u 2 e − ( 1 + u 2 ) t 2 /2 d u .
عبارت زیر را تعریف میکنیم:
h ( t ) = ∫ 0 1 e − ( 1 + x 2 ) t 2 / 2 1 + x 2 d x . \large h ( t ) = \int _ { 0 } ^ { 1 } \frac { e ^ { - ( 1 + x ^ 2 ) t ^ 2 / 2 } } { 1 + x ^ 2 } \, d x . h ( t ) = ∫ 0 1 1 + x 2 e − ( 1 + x 2 ) t 2 /2 d x .
با محاسبات بالا، g ′ ( t ) = − 2 h ′ ( t ) g' ( t ) = - 2 h' ( t) g ′ ( t ) = − 2 h ′ ( t ) g ( t ) = − 2 h ( t ) + C g ( t ) = - 2 h ( t) + C g ( t ) = − 2 h ( t ) + C C C C t t t g ( 0 ) = 0 g ( 0 ) = 0 g ( 0 ) = 0
h ( 0 ) = ∫ 0 1 1 1 + x 2 d x = tan − 1 x ∣ 0 1 = π 4 , \large h ( 0 ) = \int _ { 0 } ^ { 1 } \frac { 1 } { 1 + x ^ 2 } \, d x = \tan ^ { - 1 } x \Bigg \vert _ { 0 } ^ { 1 } = \frac { \pi } { 4 } , h ( 0 ) = ∫ 0 1 1 + x 2 1 d x = tan − 1 x 0 1 = 4 π ,
خواهیم داشت:
0 = − π / 2 + C ⟹ C = π / 2 \large 0 = -\pi/2 + C \implies C = \pi/2 0 = − π /2 + C ⟹ C = π /2
در نهایت، با t → ∞ t \to \infty t → ∞ g ( ∞ ) = − 2 h ( ∞ ) + π / 2 = π / 2 g(\infty) = -2h(\infty) + \pi/2 = \pi/2 g ( ∞ ) = − 2 h ( ∞ ) + π /2 = π /2
∫ 0 ∞ e − x 2 / 2 d x = π / 2 . \large \int _ { 0 } ^ { \infty } e ^ { - x ^ 2 / 2 } \, d x = \sqrt { \small\pi / 2 } . ∫ 0 ∞ e − x 2 /2 d x = π /2 .
مثال سوم مشتق انتگرال
فرض کنید a a a b b b c > 0 c > 0 c > 0
∫ − ∞ ∞ e − c x 2 erf ( a x + b ) d x = π c erf ( b c a 2 + c ) \large \int _ { - \infty } ^ { \infty } e ^ { - c x ^ { 2 } } \operatorname {erf} ( a x + b ) \, \mathrm { d } x = \sqrt { \frac { \pi } { c } } \operatorname {erf} \left ( \frac { b \sqrt { c } } { \sqrt { a ^ { 2 } + c } } \right ) ∫ − ∞ ∞ e − c x 2 erf ( a x + b ) d x = c π erf ( a 2 + c b c )
در عبارت بالا، e r f \mathrm{erf} erf تابع خطا را نشان میدهد.
حل: تساوی زیر را تعریف میکنیم:
I ( a , b , c ) = ∫ − ∞ ∞ e − c x 2 erf ( a x + b ) d x \large I ( a , b , c ) = \int _ { - \infty } ^ { \infty } e ^ { - c x ^ { 2 } } \operatorname {erf} ( a x + b ) \mathrm { d } x I ( a , b , c ) = ∫ − ∞ ∞ e − c x 2 erf ( a x + b ) d x
اگر از تغییر متغیر u = c x u = \sqrt {c} x u = c x
I ( a , b , c ) = ∫ − ∞ ∞ e − u 2 erf ( a c u + b ) d u c = 1 c I ( a c , b , 1 ) \large I ( a , b , c ) = \int _ { - \infty } ^ { \infty } e ^ { -u ^ { 2 } } \operatorname {erf} \left ( \frac { a } { \sqrt { c } } u + b \right ) \frac { \mathrm { d } u } { \sqrt { c } } = \frac { 1 } { \sqrt { c } } I \left ( \frac { a } { \sqrt { c } } , b , 1 \right ) I ( a , b , c ) = ∫ − ∞ ∞ e − u 2 erf ( c a u + b ) c d u = c 1 I ( c a , b , 1 )
بنابراین، بر یافتن J ( a , b ) , I ( a , b , 1 ) J ( a , b ) , I ( a , b , 1 ) J ( a , b ) , I ( a , b , 1 )
erf x = 2 π ∫ 0 x e − t 2 d t ⟹ erf ′ ( x ) = 2 π e − x 2 \large \operatorname {erf} x = \frac { 2 } { \sqrt { \pi } } \int _ { 0 } ^ { x } e ^ { - t ^ { 2 } } \mathrm { d } t \quad \Longrightarrow \quad \operatorname {erf} ^ { \prime }( x ) = \frac { 2 } { \sqrt { \pi } } e ^ { - x ^ { 2 } } erf x = π 2 ∫ 0 x e − t 2 d t ⟹ erf ′ ( x ) = π 2 e − x 2
با مشتقگیری از انتگرال نسبت به a a a
∂ J ∂ a = ∫ − ∞ ∞ e − x 2 ∂ ∂ a erf ( a x + b ) d x = 2 π ∫ − ∞ ∞ x e − x 2 e − ( a x + b ) 2 d x \large \frac { \partial J } { \partial a } = \int _ { - \infty } ^ { \infty } e ^ { - x ^ { 2 } } \frac { \partial } { \partial a } \operatorname {erf} ( a x + b ) \mathrm { d } x = \frac { 2 } { \sqrt { \pi } } \int _ { - \infty } ^ { \infty } x e ^ { - x ^ { 2 } } e ^ { - ( a x + b ) ^ { 2} } \mathrm { d } x ∂ a ∂ J = ∫ − ∞ ∞ e − x 2 ∂ a ∂ erf ( a x + b ) d x = π 2 ∫ − ∞ ∞ x e − x 2 e − ( a x + b ) 2 d x
نمای e e e
x 2 + ( a x + b ) 2 = ( a 2 + 1 ) x 2 + 2 a b x + b 2 = ( a 2 + 1 ) ( x + a b a 2 + 1 ) 2 + b 2 a 2 + 1 \large x ^ { 2 } + ( a x + b ) ^ { 2 } = \left ( a ^ { 2 } + 1 \right ) x ^ { 2 } + 2 a b x + b ^ { 2 } = \left ( a ^ { 2 } + 1 \right ) \left ( x + \frac { a b }{ a ^ { 2 } + 1 } \right ) ^ { 2 } + \frac { b ^ { 2 } } { a ^ { 2 } + 1 } x 2 + ( a x + b ) 2 = ( a 2 + 1 ) x 2 + 2 ab x + b 2 = ( a 2 + 1 ) ( x + a 2 + 1 ab ) 2 + a 2 + 1 b 2
در نتیجه، مشتق برابر است با:
∂ J ∂ a = 2 π exp ( − b 2 a 2 + 1 ) ∫ − ∞ ∞ x exp [ − ( a 2 + 1 ) ( x + a b a 2 + 1 ) 2 ] d x = 2 π exp ( − b 2 a 2 + 1 ) ∫ − ∞ ∞ ( v − a b a 2 + 1 ) exp [ − ( a 2 + 1 ) v 2 ] d v [ v = x + a b / ( a 2 + 1 ) ] = 2 π ( − a b a 2 + 1 ) exp ( − b 2 a 2 + 1 ) ∫ − ∞ ∞ exp [ − ( a 2 + 1 ) v 2 ] d v [ using oddness of v e − ( a 2 + 1 ) v 2 ] = 2 π ( − a b a 2 + 1 ) exp ( − b 2 a 2 + 1 ) π a 2 + 1 [ ( i ) ] = − 2 a b ( a 2 + 1 ) 3 / 2 exp ( − b 2 a 2 + 1 ) \large \begin {aligned} \frac { \partial J } { \partial a } & = \frac { 2 } { \sqrt { \pi } } \exp \left ( \frac { - b ^ { 2 } } { a ^ { 2 } + 1 } \right ) \int _ { - \infty } ^ { \infty } x \exp \left [ - \left ( a ^ { 2 } + 1 \right ) \left ( x + \frac { a b }{ a ^ { 2 } + 1 } \right ) ^ { 2 } \right ] \mathrm { d } x \\ & = \frac { 2 } { \sqrt { \pi } } \exp \left ( \frac { - b ^ { 2 } }{ a ^ { 2 } + 1 } \right ) \int _ { - \infty } ^ { \infty } \left ( v - \frac { a b } { a ^ { 2 } + 1 } \right ) \exp \left [ - \left ( a ^ { 2 } + 1 \right ) v ^ { 2 } \right ] \mathrm { d } v \quad \left [ v = x + a b / \left ( a ^ { 2 } + 1 \right ) \right ] \\ & = \frac { 2 }{ \sqrt { \pi } } \left ( - \frac { a b } { a ^ { 2 } + 1 } \right ) \exp \left ( \frac { - b ^ { 2 } } { a ^ { 2 } + 1 } \right ) \int _ { - \infty } ^ { \infty } \exp \left [ - \left ( a ^ { 2 } + 1 \right ) v ^ { 2 } \right ] \mathrm { d } v \quad \left [ \text { using oddness of } v e ^ { - \left ( a ^ { 2 } + 1 \right ) v ^ { 2 } } \right ] \\ & = \frac { 2 } { \sqrt { \pi } } \left ( - \frac { a b } { a ^ { 2 } + 1 } \right ) \exp \left ( \frac { - b ^ { 2 } } { a ^ { 2 } + 1 } \right ) \frac { \sqrt { \pi } } { \sqrt { a ^ { 2 } + 1 } } \quad [ ( i ) ] \\ & = \frac { - 2 a b } { \left ( a ^ { 2 } + 1 \right ) ^ { 3 / 2 } } \exp \left ( \frac { -b ^ { 2 } } { a ^ { 2 } + 1 } \right ) \end {aligned} ∂ a ∂ J = π 2 exp ( a 2 + 1 − b 2 ) ∫ − ∞ ∞ x exp − ( a 2 + 1 ) ( x + a 2 + 1 ab ) 2 d x = π 2 exp ( a 2 + 1 − b 2 ) ∫ − ∞ ∞ ( v − a 2 + 1 ab ) exp [ − ( a 2 + 1 ) v 2 ] d v [ v = x + ab / ( a 2 + 1 ) ] = π 2 ( − a 2 + 1 ab ) exp ( a 2 + 1 − b 2 ) ∫ − ∞ ∞ exp [ − ( a 2 + 1 ) v 2 ] d v [ using oddness of v e − ( a 2 + 1 ) v 2 ] = π 2 ( − a 2 + 1 ab ) exp ( a 2 + 1 − b 2 ) a 2 + 1 π [( i )] = ( a 2 + 1 ) 3/2 − 2 ab exp ( a 2 + 1 − b 2 )
برای (i i i
∫ − ∞ ∞ e − x 2 d x = π , Γ ( 1 2 ) = π \large \int _ { - \infty } ^ { \infty } e ^ { - x ^ { 2 } } \mathrm { d } x = \sqrt { \pi } \quad \text { , } \quad \Gamma \left ( \frac { 1 } { 2 } \right ) = \sqrt { \pi } ∫ − ∞ ∞ e − x 2 d x = π , Γ ( 2 1 ) = π
بنابراین، وقتی a → − ∞ a \to - \infty a → − ∞ J ( a , b ) → 0 J ( a , b ) \to 0 J ( a , b ) → 0
J ( a , b ) = − 2 b ∫ − ∞ a x ( x 2 + 1 ) 3 / 2 exp ( − b 2 x 2 + 1 ) d x \large J ( a , b ) = - 2 b \int _ { - \infty } ^ { a } \frac { x } { \left ( x ^ { 2 } + 1 \right ) ^ { 3 / 2 } } \exp \left ( \frac { - b ^ { 2 } } { x ^{ 2 } + 1 } \right ) \mathrm { d } x J ( a , b ) = − 2 b ∫ − ∞ a ( x 2 + 1 ) 3/2 x exp ( x 2 + 1 − b 2 ) d x
از تغییر متغیر u 2 = b 2 / ( 1 + x 2 ) u ^ 2 = b ^ 2 / ( 1 + x ^ 2 ) u 2 = b 2 / ( 1 + x 2 )
2 u d u = − 2 b 2 x ( 1 + x 2 ) 2 d x = 1 1 + x 2 − 2 b 2 x ( 1 + x 2 ) 3 / 2 d x = u b ( − 2 b 2 x ( 1 + x 2 ) 3 / 2 d x ) \large 2 u \mathrm { d } u = \frac { - 2 b ^ { 2 } x } { \left ( 1 + x ^ { 2 } \right ) ^ { 2 } } \mathrm { d } x = \frac { 1 } { \sqrt { 1 + x ^ { 2 } } } \frac { - 2 b ^ { 2 } x }{ \left ( 1 + x ^ { 2 } \right ) ^ { 3 / 2 } } \mathrm { d } x = \frac { u } { b } \left ( \frac { - 2 b ^ { 2 } x } { \left ( 1 + x ^ { 2 } \right ) ^ { 3 / 2 } } \mathrm { d } x \right ) 2 u d u = ( 1 + x 2 ) 2 − 2 b 2 x d x = 1 + x 2 1 ( 1 + x 2 ) 3/2 − 2 b 2 x d x = b u ( 1 + x 2 ) 3/2 − 2 b 2 x d x
و
d u = − b x d x ( 1 + x 2 ) 3 / 2 \large \mathrm { d } u = \frac { - b x \mathrm { d } x }{ \left ( 1 + x ^ { 2 } \right ) ^ { 3 / 2 } } d u = ( 1 + x 2 ) 3/2 − b x d x
بنابراین، J ( a , b ) J(a,b) J ( a , b )
J ( a , b ) = 2 ∫ 0 b / 1 + a 2 exp ( − u 2 ) d u = π erf ( b 1 + a 2 ) \large J ( a , b ) = 2 \int _ { 0 } ^ { b / \sqrt { 1 + a ^ { 2 } } } \exp \left ( - u ^ { 2 } \right ) \mathrm { d } u = \sqrt { \pi } \operatorname {erf} \left ( \frac { b } { \sqrt { 1 + a ^ { 2 } } } \right ) J ( a , b ) = 2 ∫ 0 b / 1 + a 2 exp ( − u 2 ) d u = π erf ( 1 + a 2 b )
و تساوی به شکل زیر اثبات میشود:
I ( a , b , c ) = 1 c J ( a c , b ) = π c erf ( b 1 + a 2 / c ) = π c erf ( b c c + a 2 ) \large \begin {align*} I ( a , b , c ) & = \frac { 1 } { \sqrt { c } } J \left ( \frac { a } { \sqrt { c } } , b \right ) = \sqrt { \frac { \pi } {c } } \operatorname {erf} \left ( \frac { b } { \sqrt { 1 + a ^ { 2 } / c } } \right ) \\ & = \sqrt { \frac { \pi } { c } } \operatorname {erf} \left ( \frac { b \sqrt { c } }{ \sqrt { c + a ^ { 2 } } } \right ) \end {align*} I ( a , b , c ) = c 1 J ( c a , b ) = c π erf ( 1 + a 2 / c b ) = c π erf ( c + a 2 b c )
مثال چهارم مشتق انتگرال
البته مثالهایی نیز وجود دارند که روش مشتق انتگرال در آنها کاربرد ندارد. برای مثال، فرض کنید میخواهیم انتگرال زیر را محاسبه کنیم:
∫ 0 ∞ sin x x d x \large \int _ { 0 } ^ { \infty } \frac { \sin x } { x } \, d x ∫ 0 ∞ x sin x d x
با استفاده از تغییر متغیر u = x / t u = x / t u = x / t t ≠ 0 t \neq 0 t = 0
∫ 0 ∞ sin x x d x = ∫ 0 ∞ sin t u u d u = g ( t ) . \large \int _ { 0 } ^ { \infty } \frac { \sin x } { x } \, d x = \int _ { 0 } ^ { \infty } \frac { \sin t u } { u } \, d u = g ( t ) . ∫ 0 ∞ x sin x d x = ∫ 0 ∞ u sin t u d u = g ( t ) .
مشتق انتگرال عبارت زیر را نتیجه میدهد:
0 = g ′ ( t ) = ∫ 0 ∞ cos t u d u \large 0 = g' ( t ) = \int _ { 0 } ^ { \infty } \cos t u \, d u 0 = g ′ ( t ) = ∫ 0 ∞ cos t u d u
که بیمعنی است. مشکل این است که تابع f ( x , t ) = sin t x / x f ( x , t ) = \sin t x / x f ( x , t ) = sin t x / x ∂ f / ∂ t \partial f / \partial t ∂ f / ∂ t x = 0 x = 0 x = 0
مثال پنجم مشتق انتگرال
انتگرال معین زیر را محاسبه کنید:
∫ 0 2 π e cos θ cos ( sin θ ) d θ . \large \int _ { 0 } ^ { 2 \pi } e ^ { \cos \theta } \cos ( \sin \theta ) \, d \theta . ∫ 0 2 π e c o s θ cos ( sin θ ) d θ .
از تابع زیر کمک بگیرید:
f ( t ) = ∫ 0 2 π e t cos θ cos ( t sin θ ) d θ \large f ( t ) = \int _ { 0 } ^ { 2 \pi } e ^ { t \cos \theta } \cos ( t \sin \theta ) \, d \theta f ( t ) = ∫ 0 2 π e t c o s θ cos ( t sin θ ) d θ
حل: با توجه به تابع f f f
t f ′ ( t ) = t ∫ 0 2 π e t cos θ [ cos θ cos ( t sin θ ) − sin θ sin ( t sin θ ) ] d θ = ∫ 0 2 π ∂ ∂ θ [ e t cos θ sin ( t sin θ ) ] d θ = [ e t cos θ sin ( t sin θ ) ] 0 2 π = 0 \large \begin {array} {rcl} t f' ( t ) & = & \displaystyle t \int _ 0 ^ { 2 \pi } e ^ { t \cos \theta } \big [ \cos \theta \cos ( t \sin \theta ) - \sin \theta \sin ( t \sin \theta ) \big ] \, d \theta \\ & = & \displaystyle \int _ 0 ^ { 2 \pi } \frac { \partial } { \partial \theta } \big [ e ^ { t \cos \theta } \sin ( t \sin \theta ) \big ] \, d \theta \\ & = & \Big [ e ^ { t \cos \theta } \sin ( t \sin \theta ) \Big ] _ 0 ^ { 2 \pi } \; = \; 0 \end {array} t f ′ ( t ) = = = t ∫ 0 2 π e t c o s θ [ cos θ cos ( t sin θ ) − sin θ sin ( t sin θ ) ] d θ ∫ 0 2 π ∂ θ ∂ [ e t c o s θ sin ( t sin θ ) ] d θ [ e t c o s θ sin ( t sin θ ) ] 0 2 π = 0
از آنجا که f ( 0 ) = 2 π f ( 0 ) = 2 \pi f ( 0 ) = 2 π f ( 1 ) = 2 π f ( 1 ) = 2 \pi f ( 1 ) = 2 π
مثال ششم مشتق انتگرال
انتگرال زیر را محاسبه کنید:
∫ 0 1 ( x ln x ) 50 d x . \large \int _ { 0 } ^ { 1 } ( x \ln x ) ^ { 5 0 } \, d x . ∫ 0 1 ( x ln x ) 50 d x .
حل: از روش مشتق انتگرال استفاده میکنیم. عبارت زیر را در نظر بگیرید:
F ( a ) = ∫ 0 1 x a dx = 1 a + 1 \large F ( a ) = \int _ 0 ^ 1 x ^ a \text {dx} = \dfrac { 1 }{ a + 1 } F ( a ) = ∫ 0 1 x a dx = a + 1 1
با ۵۰ بار مشتقگیری از F F F a a a
F ( 50 ) ( a ) = ∫ 0 1 ln 50 ( x ) x a dx = 50 ! ( a + 1 ) 51 \large F ^ { ( 5 0 ) } ( a ) = \int _ 0 ^ 1 \ln ^ { 5 0 }( x ) x ^ a \text {dx} = \dfrac { 5 0 ! } { ( a + 1 ) ^ { 5 1 } } F ( 50 ) ( a ) = ∫ 0 1 ln 50 ( x ) x a dx = ( a + 1 ) 51 50 !
جواب مسئله با قرار دادن a = 50 a = 50 a = 50
F ( 50 ) ( 50 ) = ∫ 0 1 ln 50 ( x ) x 50 dx = 50 ! 5 1 51 \large F ^ { ( 50 ) } ( 5 0 ) = \int _ 0 ^ 1 \ln ^ { 5 0 }( x ) x ^ { 5 0 } \text {dx} = \boxed { \dfrac { 5 0 ! } { 5 1 ^ { 5 1 } } } F ( 50 ) ( 50 ) = ∫ 0 1 ln 50 ( x ) x 50 dx = 5 1 51 50 !
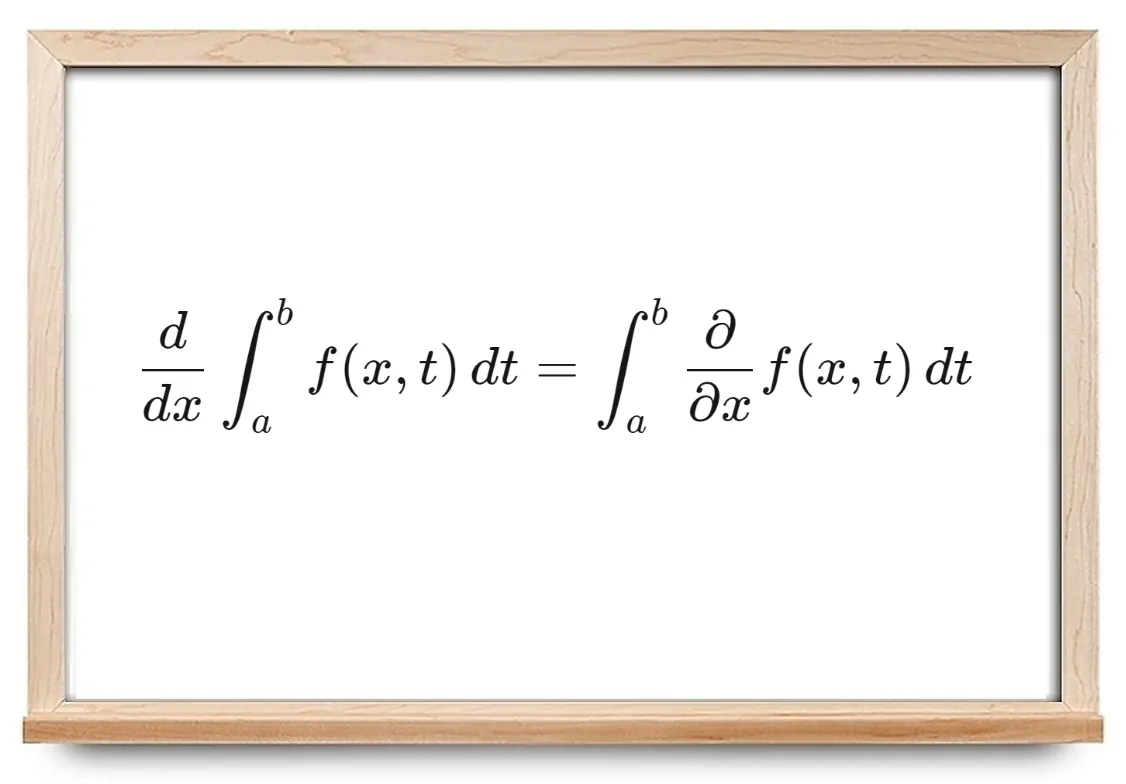













سلام من فقط اثبات فرمول مشتق انتگرال را میخواستم ولی خیلی پیچیده توضیح داده بودین ، اگه یه قسمت چکیده آخرش داشتین که کمی ساده تر کل مطالب این صفحه را مرور میکرد خیلی خوب میشد
سلام. اثبات مورد نظر به متن اضافه شد.
از همراهیتان با مجله فرادرس سپاسگزاریم.