تابع خطا — از صفر تا صد

در آموزش‌های پیشین مجله فرادس با انتگرال گاوسی آشنا شدیم. در این آموزش با تابع خطا آشنا می‌شویم که کاربرد فراوانی در علم مواد، آمار و احتمال، معادلات دیفرانسیل با مشتقات جزئی و... دارد.

تعریف تابع خطا

در ریاضیات، تابع خطا (Error Function) که تابع خطای گاوس (Gauss Error Function) نیز نامیده می‌شود، به صورت زیر تعریف می‌شود:

$$ \large \text{erf} ( x ) = \frac { 1 } { \sqrt { \pi}} \int _{- x } ^ { x } { e ^ { - t ^ 2 } } d t = \frac { 2 } { \sqrt { \pi}} \int _{0 } ^ { x } { e ^ { - t ^ 2 } } d t. $$

این انتگرال یک تابع ویژه (غیرمقدماتی) و سیگموئید است که اغلب در احتمال، آمار و معادلات دیفرانسیل با مشتقات جزئی برای بیان پراکندگی به کار می‌رود. در آمار، برای مقادیر نامنفی $$ X $$، تابع خطا این‌گونه بیان می‌شود: برای یک متغیر تصادفی $$Y$$ که به صورت نرمال با میانگین $$0$$ و واریانس $$1/2$$ توزیع شده است، تابع خطای $$\text{erf}(X)$$ برابر با احتمال $$Y$$ در بازه $$ [- X , X] $$ است.

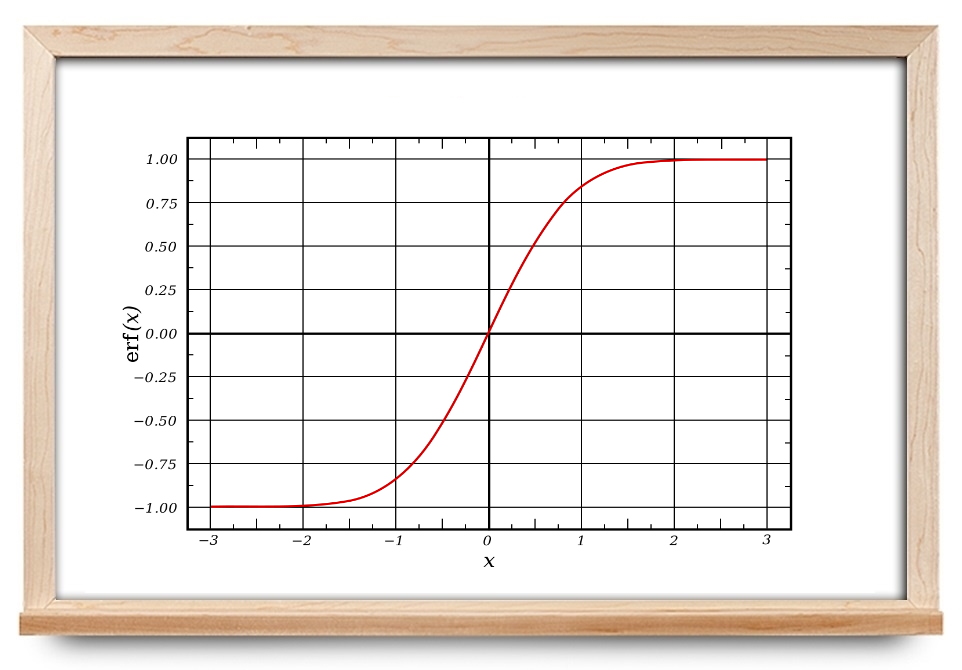
شکل زیر، نمودار تابع خطا را نشان می‌دهد.

تابع خطای مکمل (Complementary Error Function) به صورت $$\text{erfc}$$ نوشته شده و به صورت $$ \text{erfc}(x) = 1 - \text{erf}(x)$$ تعریف می‌شود.

تابع خطای موهومی (Imaginary Error Function) نیز به صورت $$\text{erfi}( x) = - \text{i erf}(\text{i}x)$$ بیان می‌شود که در آن، $$\text{i}$$ واحد موهومی است.

نام تابع خطا و مخفف آن، $$\text{erf}$$ توسط جیمز وایتبرد لی گلیشر (James Whitbread Lee Glaisher) در سال ۱۸۷۱ در رابطه با نظریه احتمال و نظریه خطاها بیان شد. همچنین، تابع خطای مکمل توسط گلیشر به صورت مجزا در یک مقاله در همان سال مورد بحث قرار گرفت. برای تسهیل بیان خطا با تابع چگالیِ $$  f ( x ) = \left ( \frac { c } { \pi } \right ) ^ { \tfrac { 1 } { 2 } } e ^ { - c x ^ 2 } $$ با توزیع نرمال، گلیشر شانس خطای بین $$ p $$ و $$ q $$ را به صورت زیر محاسبه کرد:

$$ \large \left ( \frac { c } { \pi } \right ) ^ { \tfrac { 1 } { 2 } } \int _ p ^ q e ^ { - c x ^ 2 } d x= \tfrac { 1 } { 2 } \left ( \operatorname { e r f } ( q \sqrt { c } ) -\operatorname { e r f } ( p \sqrt { c } ) \right ) . $$

کاربردهای تابع خطا

وقتی نتایج دنباله‌ای از اندازه‌گیری‌ها با یک توزیع نرمال با انحراف معیار $$ \sigma$$ و امید ریاضی $$0$$ توصیف شود، آنگاه $$\textstyle\operatorname{erf}\left(\frac{a}{\sigma \sqrt{2}}\right) $$ احتمال خطای یک اندازه‌گیری تکی بین $$-a$$ و $$ a $$ است ($$a$$ مثبت است). این فرمول، برای مثال، در نرخ خطای بیت یک سیستم مخابرات دیجیتال کاربرد دارد.

توابع خطا و مکمل خطا، در حل معادله گرما، هنگامی که شرایط مرزی با تابع پله هویساید داده شده باشد، کاربرد دارند.

تابع خطا و تقریب‌های آن را می‌توان برای تخمین نتایجِ با احتمال بالا یا احتمال کم نیز مورد استفاده قرار داد. برای متغیر تصادفی $$ X \sim \operatorname{Norm}[\mu,\sigma] $$ و ثابت $$ L<\mu $$، داریم:

$$ \large \Pr [ X \leq L ] = \frac { 1 } {2 } + \frac { 1 } { 2 } \operatorname {erf} \left ( \frac { L - \mu } { \sqrt { 2 } \sigma } \right ) \approx A \exp \left ( - B \left ( \frac { L - \mu }{ \sigma } \right ) ^ 2 \right ) $$

که در آن، $$ A $$ و $$ B$$ اعداد ثابت معینی هستند. اگر $$L$$ به اندازه کافی دور از میانگین باشد، یعنی $$ \mu-L \geq \sigma\sqrt{\ln{k}} $$، آنگاه داریم:

$$ \large \Pr [ X \leq L ] \leq A \exp ( - B \ln { k } ) = \frac { A } { k ^ B } $$

بنابراین، وقتی $$k \to \infty $$، احتمال به صفر میل می‌کند.

ویژگی‌های تابع خطا

ویژگی $$ \operatorname{erf} (-z) = -\operatorname{erf} (z) $$ تابع خطا بدین معنی است که این تابع، یک تابع فرد است. این ویژگی از این واقعیت ناشی می‌شود که انتگرالده $$ e^{-t^2} $$ یک تابع زوج است.

برای هر عدد مختلط $$ z $$، رابطه $$ \operatorname{erf} (\overline{z}) = \overline{\operatorname{erf}(z)}$$ برقرار است که در آن، $$ \overline{z}$$ مزدوج مختلط $$ z $$ را نشان می‌دهد.

انتگرالده $$ f = \text{exp}(-z ^ 2 ) $$ و $$ f = \text{erf} ( z ) $$ در صفحه $$z$$ در شکل ۲ (الف) و (ب) نشان داده شده است. سطح $$\text{Im}(f)=0$$ با یک خط ضخیم سبز نشان داده شده است. مقادیر صحیح منفی $$\text{Im}(f)$$ با خطوط ضخیم قرمز و مقادیر صحیح مثبت $$\text{Im}(f)$$ با خطوط آبی ضخیم نشان داده شده‌اند. همچنین، سطوح متوسط $$\text{Im}(f)$$ ثابت با خطوط نازک سبز و سطوح متوسط $$ \text{Re} ( f) $$ ثابت با خطوط نازک قرمز برای مقادیر منفی و با خطوط آبی نازک برای مقادیر مثبت نمایش داده شده‌اند.

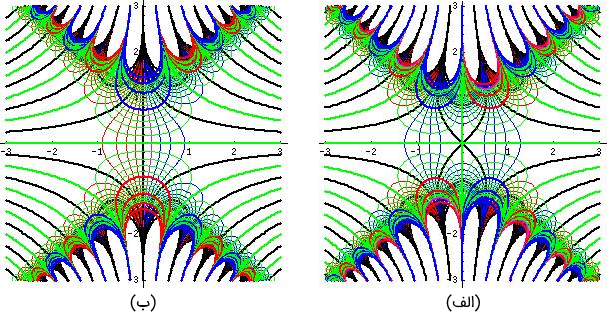
تابع خطا در $$ + \infty $$ دقیقاً برابر با ۱ است (انتگرال گاوسی را ببینید). همچنین، تابع خطا روی محور حقیقی، در $$ z \to + \infty $$ به $$1$$ و در $$ z \to - \infty $$ به $$-1$$ میل می‌کند. در محور موهومی نیز، به $$ \pm i \infty $$ میل خواهد کرد.

تابع خطا و سری تیلور

تابع خطا یک تابع تام (Entire function) است؛ بدین معنی که هیچ تکینگی ندارد (به جز در بینهایت) و بسط تیلور آن همیشه همگرا می‌شود.

نمی‌توان انتگرال را به فرم بسته و برحسب توابع مقدماتی نوشت، اما با گسترش انتگرالده $$ e ^ {-z^2}$$ به بسط مک‌لورن و انتگرال‌گیری جمله به جمله، می‌توان سری مک‌لورن تابع خطا را به دست آورد:

$$ \large \operatorname {erf} ( z ) = \frac { 2 } { \sqrt { \pi } } \sum _ { n = 0 } ^ \infty \frac { ( - 1 )^ n z^ { 2 n +1 } }{ n! ( 2 n + 1 ) } = \frac { 2 } { \sqrt { \pi } } \left ( z - \frac { z ^ 3 } { 3 } + \frac { z ^ 5 } {1 0} - \frac { z ^ 7 } { 4 2 } + \frac { z ^ 9 } { 2 1 6 } - \cdots \right ) $$

که برای هر عدد مختلط $$ z $$ برقرار است. برای محاسبه سری بالا، فرمول جایگزین زیر مفید است:

$$ \large \operatorname {erf} ( z ) = \frac { 2 } { \sqrt { \pi } } \sum _ { n = 0 } ^ \infty \left ( z \prod _ { k = 1 } ^ n { \frac { - ( 2 k - 1 ) z ^ 2 } { k ( 2 k + 1 ) } } \right ) = \frac { 2 } { \sqrt { \pi } } \sum _ { n = 0 } ^ \infty \frac { z } { 2 n + 1 } \prod _ { k = 1 } ^ n \frac { - z ^ 2 } { k } $$

زیرا $$ \frac{-(2k-1) z^2}{k (2k+1)} $$ ضرب $$k$$اُمین جمله در $$ (k+1)$$اُمین جمله را توصیف می‌کند (با توجه به اینکه $$ z $$ اولین جمله است).

بسط مک‌لورن تابع خطای موهومی نیز به صورت زیر است:‌

$$ \large \begin {align*} \operatorname {erfi} ( z ) & = \frac { 2 } { \sqrt { \pi } } \sum _ { n = 0 } ^ \infty \frac { z ^ { 2 n + 1 } } { n ! ( 2 n + 1 ) } \\ &= \frac { 2 } { \sqrt { \pi } } \left ( z + \frac { z ^3 } { 3 } + \frac { z ^ 5 } { 1 0 } + \frac { z ^ 7 } { 4 2 } + \frac { z ^ 9 } { 2 1 6 } + \cdots \right ) \end {align*}$$

که برای هر عدد مختلط $$ z $$ برقرار خواهد بود.

مشتق و انتگرال تابع خطا

مشتق تابع خطا به سادگی و با استفاده از تعریف، به صورت زیر به دست می‌آید:

$$ \large \frac { d } { d z } \operatorname {erf} ( z ) = \frac { 2 } { \sqrt { \pi } } e ^ { - z ^ 2 } . $$

بر همین اساس، مشتق تابع خطای موهومی نیز به صورت زیر خواهد بود:

$$ \large \frac { d } { d z } \operatorname {erfi} ( z ) = \frac { 2 } { \sqrt { \pi } } e ^ { z ^ 2 } . $$

پادمشتق تابع خطا نیز با کمک انتگرال‌گیری جزء به جزء به صورت زیر است:

$$ \large z \operatorname {erf} ( z ) + \frac { e ^ { - z ^ 2 } } { \sqrt { \pi } } . $$

همچنین، پادمشتق تابع خطای موهومی با انتگرال‌گیری جزء به جزء به صورت زیر به دست می‌آید:

$$ \large z \operatorname {erfi} ( z ) - \frac { e ^ { z ^ 2 } }{ \sqrt { \pi } } . $$

مشتق مراتب بالاتر تابع خطا نیز به صورت زیر بیان می‌شود:

$$ \large \operatorname {erf} ^ { ( k ) } ( z ) = \frac { 2 ( - 1 ) ^ { k - 1 } } { \sqrt { \pi } } \mathit { H } _ { k - 1 } ( z ) e ^ { - z ^ 2 } = \frac { 2 } { \sqrt { \pi } } \frac { d ^ { k - 1 } } { dz ^ { k - 1 } } \left ( e ^ { - z ^ 2 } \right ) , \qquad k = 1 , 2 , \dots $$

که در آن، $$\mathit{H}$$ چندجمله‌ای هرمیت است.

تابع خطا و سری بورمن

با استفاده از بسط بورمن (Bürmann Series) که نسبت به یک بسط تیلور، برای همه مقادیر $$ x $$ سریع‌تر همگرا می‌شود، می‌توان تابع خطا را نوشت:

$$ \large \begin {align*}
\operatorname {erf} ( x ) & = \frac 2 { \sqrt { \pi } } \text{sgn} ( x ) \sqrt { 1 - e ^ { - x ^ 2 } } \left ( 1 - \frac { 1 } { 1 2 } \left ( 1 - e ^ { - x ^ 2 } \right ) - \frac { 7 } { 4 8 0 } \left ( 1 - e ^ { - x ^ 2 } \right ) ^ 2 \\ - \frac { 5 } { 8 9 6 } \left ( 1 - e ^ { - x ^ 2 } \right ) ^ 3 - \frac { 7 8 7 } { 2 7 6 4 8 0 } \left ( 1 - e ^ { - x ^ 2 } \right ) ^ 4 - \cdots \right ) \\[10pt]
& = \frac { 2 } { \sqrt { \pi } } \text{sgn} ( x ) \sqrt { 1 - e ^ { -x ^ 2 } } \left ( \frac { \sqrt { \pi } } { 2 } + \sum _ { k =1 } ^ \infty c _ k e ^ { - k x ^ 2 } \right ) .
\end{align*} $$

با نگه داشتن تنها دو ضریب اول و انتخاب $$ c _ 1 = \frac {31}{200}$$ و $$ c _ 2 = - \frac {341}{8000}$$، تقریب حاصله بزرگ‌ترین خطای نسبی آن را در $$ x = \pm 1.3796$$ نشان می‌دهد که کمتر از $$3.6127 \times 10^ {-3}$$ است:

$$ \large \operatorname {erf} ( x ) \approx \frac { 2 } { \sqrt { \pi } } \text{sgn} ( x ) \sqrt { 1 - e ^ { - x ^ 2 } } \left ( \frac { \sqrt { \pi } } { 2 } + \frac { 3 1 } { 2 00 } e ^ { - x ^ 2 } - \frac { 3 4 1 } { 8 0 0 0 } e ^ { - 2 x ^ 2 } \right ) . $$

تابع معکوس خطا

برای عدد مختلط $$ z $$، عدد مختلط یکتای $$ w$$ وجود ندارد که در $$ \text{erf}(w) = z $$ صدق کند، بنابراین، تابع معکوس چندمقداره خواهد بود. با این حال، برای $$ -1<x < 1$$، یک عدد حقیقی یکتا وجود دارد که با $$ \text{erf}^{-1} (x)$$ مشخص شده و در معادله $$ \operatorname{erf}\left(\operatorname{erf}^{-1}(x)\right) = x $$ صدق می‌کند.

تابع خطای معکوس معمولاً با دامنه $$(-1,1)$$ تعریف می‌شود، و در بسیاری از سیستم‌های جبری کامپیوتری به همین دامنه محدود است. البته، این دامنه را می‌توان به قرص $$ |z|< 1$$ در صفحه مختلط نیز با استفاده از سری مک‌لورن بسط داد:

$$ \large \operatorname {erf} ^ { - 1 } ( z ) = \sum _ { k = 0 } ^ \infty \frac { c _ k } { 2 k + 1 } \left ( \frac { \sqrt { \pi } } { 2 } z \right ) ^ { 2 k + 1 } $$

که در آن، $$ c _ 0 = 1 $$ و داریم:

$$ \large c _ k = \sum _ { m = 0 } ^ { k - 1 } \frac { c _ m c _ { k - 1 - m } } { ( m + 1 ) ( 2 m + 1 ) } = \left\{ 1 , 1 , \frac { 7 } { 6 } , \frac { 1 2 7 } { 9 0 } , \frac { 4 3 6 9 } { 2 5 2 0 } , \frac { 3 4 8 0 7 } { 1 6 2 0 0 } , \ldots \right\} . $$

بنابراین، بسط سری زیر را خواهیم داشت (عوامل مشترک صورت‌ها و مخرج‌ها حذف شده‌اند):

$$ \large \operatorname {erf} ^ { – 1 } ( z ) = \tfrac { 1 }{ 2 } \sqrt { \pi } \left ( z + \frac { \pi } { 1 2 }z ^ 3 + \frac { 7 \pi ^ 2 } { 4 8 0 } z ^ 5 + \frac { 1 2 7 \pi ^ 3 } { 4 0 3 20 } z ^ 7 \\ + \frac { 4 3 6 9 \pi ^ 4 } { 5 8 0 6 0 8 0} z ^ 9 + \frac {3 4 8 0 7 \pi ^ 5 } {1 8 2 4 76 8 0 0 } z ^ { 1 1 } + \cdots \right ) . $$

برای $$ |z|<1$$، داریم: $$\operatorname{erf}\left(\operatorname{erf}^{-1}(z)\right)=z $$.

تابع خطای مکمل معکوس نیز به صورت زیر تعریف می‌شود:

$$ \large \operatorname {erfc} ^ { - 1 } ( 1 - z ) = \operatorname {erf} ^ { - 1 } (z ) . $$

برای $$ x $$ حقیقی، یک عدد حقیقی یکتای $$ \text{erfi}^{-1}(x ) $$ وجود دارد که در $$ \operatorname{erfi}\left(\operatorname{erfi}^{-1}(x)\right)=x $$ صدق می‌کند. تابع خطای موهومی معکوس به صورت $$\text{erfi}^{-1} ( x) $$ تعریف می‌شود.

برای هر عدد حقیقی $$ x $$، می‌توان از روش نیوتن برای $$\text{erfi}^{-1} ( x) $$ استفاده کرد. برای $$ -1 \leq x \leq 1$$، سری مک‌لورن زیر همگرا می‌شود:

$$ \large \operatorname {erfi} ^ { - 1 } ( z )= \sum _ { k = 0 } ^ \infty \frac { (- 1 ) ^ k c _ k } { 2 k + 1 } \left ( \frac { \sqrt { \pi } } { 2 } z \right ) ^ { 2 k + 1 } $$

که در آن، $$ c _ k $$ در بالا تعریف شد.

بسط مجانبی تابع خطا

یک بسط مجانبی مفید از تابع خطای مکمل (و در نتیجه، تابع خطا)، برای عدد حقیقی بزرگ $$ x $$ به صورت زیر است:

$$ \large \operatorname {erfc} ( x ) = \frac { e ^ { - x ^ 2 } } { x \sqrt { \pi } } \left [ 1 + \sum _ { n = 1 } ^ \infty ( - 1 ) ^ n \frac { 1 \cdot 3 \cdot 5 \cdots ( 2 n - 1 ) } { ( 2 x ^ 2) ^ n } \right ] \\ \large = \frac { e ^ { -x ^ 2 } } { x \sqrt { \pi } } \sum _ { n = 0 } ^ \infty ( - 1 ) ^ n \frac { ( 2 n - 1 ) ! ! } { ( 2 x ^ 2 ) ^ n } $$

که در آن، $$(2n-1)!!$$ فاکتوریل دوگانه $$ (2n-1)$$ را نشان می‌دهد. این سری برای هر $$x $$ محدود، واگرا می‌شود، و معنی آن، مانند بسط مجانبی، این است که برای هر $$N\in \mathcal{N}$$ داریم:

$$ \large \operatorname {erfc} ( x ) = \frac { e ^ { - x ^ 2 } } { x \sqrt { \pi } } \sum _ { n = 0 } ^ { N - 1 } ( - 1 ) ^ n \frac { ( 2 n - 1 ) ! ! } { ( 2 x ^ 2) ^ n } + R _ N ( x ) $$

وقتی $$ x \to \infty $$ باشد، باقیمانده با نماد O به صورت زیر است:

$$ \large R _ N ( x ) = O \left ( x ^ { 1 - 2 N } e ^ { -x ^ 2 } \right ) $$

در واقع، مقدار دقیق باقیمانده برابر است با:

$$ \large R _ N ( x ) : = \frac { ( - 1 ) ^ N } { \sqrt { \pi } } 2 ^ { 1 - 2 N } \frac { ( 2 N ) ! } { N ! } \int _ x ^ \infty t ^ { - 2 N } e ^ { - t^ 2 } \, d t $$

با استفاده از استقرا، به سادگی می‌توان نوشت:

$$ \large e ^ { - t ^ 2 } = - ( 2 t ) ^ { - 1 } \left ( e ^ { -t ^ 2 } \right )' $$

و از انتگرال‌گیری جزء به جزء استفاده کرد.

برای مقادیر $$ x $$ به اندازه کافی بزرگ، فقط چند جمله اول این بسط مجانبی برای به دست آوردن یک تقریب مناسب از $$ \text{erfc}(x)$$ لازم هستند. این در حالی است که برای مقادیر نه چندان بزرگ $$ x $$، بسط تیلور بالا در صفر همگرایی بسیار سریعی خواهد داشت.

بسط کسر مسلسل تابع خطای مکمل

بسط کسر مسلسل یک تابع خطای مکمل به صورت زیر است:

$$ \large \operatorname {erfc} ( z ) = \frac { z } { \sqrt { \pi } } e ^ { - z ^ 2 } \cfrac { 1 } { z ^ 2 + \cfrac { a _ 1 }{ 1 + \cfrac { a _ 2 } { z ^ 2 + \cfrac { a _ 3 } { 1 + \dotsb } } } } \qquad a _ m = \frac { m } { 2 } . $$

انتگرال تابع خطا با تابع چگالی گاوسی

انتگرال تابع خطا با تابع چگالی گاوسی به صورت زیر بیان می‌شود:

$$ \large \int _ { - \infty } ^ { \infty } \operatorname {erf} \left ( a x + b \right ) \frac { 1 } { \sqrt { 2 \pi \sigma ^ 2 } } e ^ { - \frac { ( x - \mu ) ^ 2 } { 2 \sigma ^ 2 } } \, d x = \operatorname {erf} \left [ \frac { a \mu + b } { \sqrt { 1 + 2 a ^ 2 \sigma ^ 2 } } \right ] , \qquad a , b , \mu , \sigma \in \mathbb{R} $$

بسط فاکتوریل تابع خطا

سری فاکتوریل معکوس زیر، برای $$\text{Re}(z^2)>0 $$ همگرا می‌شود:

$$ \large \begin {align}
\operatorname {erfc} z & = \frac { e ^ { - z ^ 2 } } { \sqrt { \pi } \, z } \sum _ { n = 0 } ^ \infty \frac { ( - 1) ^ n Q _ n } { { ( z ^ 2 + 1 ) } ^ { \bar { n } } } \\
& = \frac { e ^ { - z ^ 2 } } { \sqrt { \pi } \, z } \left ( 1 -\frac { 1 } { 2 } \frac { 1 } { ( z ^2 + 1 ) } + \frac { 1 } { 4 } \frac { 1 } { ( z ^ 2 + 1 ) ( z ^ 2 + 2 ) } - \cdots \right )
\end {align} $$

که در آن:

$$ \large Q _ n \stackrel { \text {def} } { = } \frac { 1 } { \Gamma ( 1 / 2 ) } \int _ 0 ^ \infty \tau ( \tau - 1 ) \cdots ( \tau - n + 1 ) \tau ^ { - 1 / 2 } e ^ { - \tau } d \tau = \sum _ { k = 0 } ^ n \left ( \frac { 1 } { 2 } \right ) ^ { \bar { k } } s (n , k ) $$

$$z ^{\bar n}$$ فاکتوریل افزایشی را نشان می‌دهد و $$ s ( n , k )$$ یک عدد استرلینگ نوع اول علامت‌دار است.

تقریب‌های عددی تابع خطا

در این بخش، تقریب‌های عددی تابع خطا را معرفی می‌کنیم.

تقریب با توابع مقدماتی

آبرامویز (Abramowitz) و استگان (Stegun) چند تقریب با دقت‌های متغیر برای تابع خطا ارائه کرده‌اند. این تقریب‌ها امکان انتخاب سریع‌ترین تقریب مناسب برای یک کاربرد مشخص را ارائه می‌دهند. یکی از این تقریب‌ها به صورت زیر است (حداکثر خطای این تقریب $$5 \times 10 ^{-4}$$ است):

$$ \large \operatorname {erf} ( x ) \approx 1 - \frac { 1 } { ( 1 + a _ 1 x + a _ 2 x ^ 2 + a _ 3 x ^ 3 + a _ 4 x ^ 4 ) ^ 4 } , \qquad x \geq 0 $$

که در آن، $$ a _ 1 = 0.278393$$، $$ a _ 2 = 0.230389$$، $$ a _ 3 = 0.000972$$ و $$a _ 4 = 0.078108 $$.

همچنین، تقریب‌های زیر را داریم:

$$ \large \operatorname {erf} ( x ) \approx 1 - ( a _ 1 t + a _ 2 t ^ 2 + a _ 3 t ^ 3 ) e ^ { - x ^2 } , \quad t = \frac { 1 } { 1 + p x } , \qquad x \geq 0 $$

(حداکثر خطا: $$2.5 \times 10 ^ { - 5 } $$)

که در آن، $$ p = 0.47047$$، $$ a _ 1 = 0.3480242$$، $$a _ 2 = -0.0958798$$ و $$ a _ 4 = 0.7478556$$.

$$ \large \operatorname {erf} ( x ) \approx 1 - \frac { 1 } { ( 1 + a _ 1 x + a _ 2 x ^ 2 + \cdots + a _ 6 x ^ 6 ) ^ { 1 6 }} , \qquad x \geq 0 $$

(حداکثر خطا: $$3 \times 10 ^ {-7}$$)

که در آن، $$ a _ 1 = 0.0705230784$$، $$ a _ 2 = 0.0422820123$$، $$ a _ 3 = 0.0092705272$$، $$ a _ 4 = 0.0001520143$$، $$ a _ 5 = 0.0002765672$$ و $$ a _ 6 = 0.0000430638$$.

$$ \large \operatorname {erf} ( x ) \approx 1 - ( a _ 1 t + a _ 2 t ^ 2 + \cdots + a _ 5 t ^ 5 ) e ^ { - x ^ 2 } , \quad t = \frac { 1 } { 1 + p x } $$

(حداکثر خطا: $$ 1.5 \times 10 ^ {-7}$$)

که در آن، $$p = 0.3275911$$، $$ a _ 1 = 0.254829592$$، $$a _ 2 = -0.284496736$$، $$ a _ 3 =1.421413741$$، $$ a _ 4 = -1.453152027$$ و $$ a _ 5 = 1.061405429$$.

همه این تقریب‌ها برای $$ x \ge 0$$ معتبر هستند. برای استفاده از این تقریب‌ها برای $$x$$های منفی، از ویژگی فرد بودن تابع خطا استفاده می‌کنیم.

حدود نمایی و یک تقریب نمایی خالص برای تابع خطای مکمل به صورت زیر هستند:

$$ \large \begin {align}
\operatorname {erfc} ( x ) & \leq \frac { 1 } { 2 } e ^ { - 2 x ^ 2 } + \frac { 1 } { 2 } e ^ { - x ^ 2 } \leq e ^ { -x ^ 2 } , \qquad x > 0 \\
\operatorname {erfc} ( x ) & \approx \frac {1 } { 6 } e^ { - x^ 2 } + \frac { 1 } { 2 } e ^ { - \frac { 4 }{ 3 } x ^ 2 } , \qquad x > 0 .
\end {align} $$

یک تخمین خوب از تابع خطای مکمل برای $$ x \in [0, \infty)$$ در سال ۲۰۰۷ توسط کاراگیانیدیس (Karagiannidis) و لیومپاس (Lioumpas) ارائه شد. این تخمین برای انتخاب مناسب پارامترهای $$\{A,B\}$$ به صورت زیر است:

$$ \large \operatorname {erfc} \left ( x \right ) \approx \frac { \left ( 1 - e ^ { - A x } \right ) e ^ { - x ^ 2 } } { B \sqrt { \pi } x } . $$

آن‌ها $$\{ A , B \} = \{ 1.98, 1.135\} $$ را تعیین کردند که یک تقریب خوب برای هر $$ x \ge 0 $$ است.

یک کران پایین تک‌جمله‌ای به صورت زیر است:

$$ \large \operatorname {erfc} ( x ) \geq \sqrt { \frac { 2 e }{ \pi } } \frac { \sqrt { \beta - 1}}{\beta} e^{- \beta x^2}, \qquad x \ge 0, \beta > 1 $$

که در آن، پارامتر $$\beta$$ را می‌توان برای کمینه کردن خطا در بازه مطلوب تقریب انتخاب کرد.

یک تقریب دیگر، توسط سرگئی وینیتسکی (Sergei Winitzki) با استفاده از تقریب پد سراسری (Global Padé Approximations) ارائه شده است:‌

$$ \large \operatorname {erf} ( x ) \approx \text{sgn} ( x ) \sqrt { 1 - \exp \left ( - x ^ 2 \frac { \frac { 4 } { \pi } + a x ^ 2 } {1 + a x ^ 2 } \right ) } $$

که در آن،

$$ \large a = \frac { 8 ( \pi - 3 ) } { 3 \pi ( 4 - \pi ) } \approx 0 . 1 4 0 0 1 2 . $$

این تقریب در همسایگی $$0$$ و همسایگی بینهایت بسیار دقیق بوده و خطای نسبی آن برای همه $$x$$های حقیقی کمتر از $$ 0.00035 $$ است. با استفاده از مقدار جایگزین $$ a \approx 0.147$$ مقدار خطای نسبی حداکثر این تقریب به حدود $$ 0.00013$$ کاهش پیدا می‌کند.

این تقریب را می‌توان برای به دست آوردن یک تقریب برای تابع خطای معکوس، معکوس کرد:

$$ \large \operatorname {erf} ^ { - 1 } ( x ) \approx \text{sgn} ( x ) \sqrt { \sqrt { \left ( \frac { 2 } { \pi a } + \frac { \ln ( 1 - x ^ 2) } { 2 } \right ) ^ 2 - \frac { \ln ( 1 - x ^ 2) } {a } } -\left ( \frac { 2 } { \pi a } + \frac { \ln ( 1 - x ^ 2 ) } { 2 } \right ) } . $$

تقریب چندجمله‌ای

یک تقریب چندجمله‌ای تابع خطا با خطای حداکثر $$ 1.2 \times 10 ^ { - 7 } $$ برای هر آرگومان حقیقی به صورت زیر است:

$$ \large \operatorname {erf} ( x ) = \begin {cases}
1 - \tau & x \ge 0 \\
\tau - 1 & x < 0
\end {cases} $$

که در آن:

$$ \large \begin {align}
\tau & = t \cdot \exp \left ( – x ^ 2 – 1 . 2 6 5 5 1 2 2 3+ 1 . 0 0 0 0 2 3 6 8 t +0 . 3 7 40 9 1 9 6 t ^ 2 \\ +0 . 0 9 6 7 8 4 1 8 t ^ 3 – 0 . 1 8 6 2 8 80 6 t ^ 4 \right . \\
& \left . \qquad \qquad \qquad + 0 . 2 7 8 8 6 8 0 7 t ^ 5 – 1 . 1 3 5 2 0 3 9 8 t ^ 6 + 1 . 4 8 8 5 1 5 8 7 t ^ 7 \\ – 0 . 8 2 2 1 5 2 2 3 t ^ 8 + 0 . 1 70 8 7 2 7 7 t ^ 9 \right )
\end {align} $$

و

$$ \large t = \frac { 1 } { 1 + 0 . 5 | x | } . $$

توابع مرتبط با تابع خطا

در این بخش، چند تابع را معرفی می‌کنیم که با تابع خطا ارتباط دارند. البته به چند مورد از این توابع در بخش‌های قبل اشاره‌ کردیم.

تابع خطای مکمل

تابع خطای مکمل با $$ \text{erfc}$$ نشان داده شده و به صورت زیر تعریف می‌شود:

$$ \large \begin {align}
\operatorname {erfc} ( x ) & = 1 - \operatorname {erf}( x ) \\[5pt]
& = \frac { 2 } { \sqrt \pi } \int _ x ^ \infty e ^ { - t ^ 2 } \, d t \\[5pt]
& = e ^ { - x ^ 2 } \operatorname {erfcx} ( x ) ,
\end {align} $$

همچنین، $$\text{erfcx}$$ تابع خطای مکمل مقیاس‌بندی شده را توصیف می‌کند. یک فرم دیگر از $$\text{erfc}(x)$$ برای $$ x $$ غیرمنفی به عنوان فرمول کریگ (Craig) شناخته می‌شود:

$$ \large \operatorname {erfc} ( x \mid x \ge 0 ) = \frac 2 \pi \int _ 0 ^ { \pi / 2 } \exp \left ( - \frac { x ^ 2 } { \sin ^ 2 \theta } \right ) \, d \theta . $$

این توصیف فقط برای مقادیر مثبت $$ x $$ معتبر است، اما می‌توان از $$ \text{erfc}(x)=2-\text{erfc}(-x)$$ در به دست آوردن $$\text{erfc}(x)$$ برای مقادیر منفی استفاده کرد. این فرم از آن جهت سودمند است که محدوده انتگرال‌گیری آن ثابت و محدود است.

تابع خطای موهومی

تابع خطای موهومی $$ \text{erfi}$$ به صورت زیر تعریف می‌شود:

$$ \large \begin {align}
\operatorname {erfi} ( x ) & = - i \operatorname {erf}( i x ) \\[5pt]
& = \frac { 2 } { \sqrt \pi } \int _ 0 ^ x e ^ { t ^ 2 } \, d t \\[5pt]
& = \frac { 2 } { \sqrt { \pi } } e ^ { x ^ 2 } D ( x ) ,
\end {align} $$

که در آن، $$ D( x ) $$ تابع داوسون (Dawson Function) است. برخلاف نام «تابع خطای موهومی»، وقتی $$ x $$ حقیقی باشد، این تابع حقیقی است.

وقتی تابع خطا برای آرگومان‌های مختلط دلخواه $$ z $$ ارزیابی شود، تابع خطای مختلط منتجه معمولاً به فرم مقیاس‌بندی شده به عنوان تابع فادیوا (Faddeeva Function) مورد بحث قرار می‌گیرد:

$$ \large w ( z ) = e ^ { - z ^ 2 } \operatorname {erfc} ( - i z ) = \operatorname {erfcx} ( - i z ) . $$

تابع توزیع تجمعی

تابع خطا اساساً مشابه تابع توزیع تجمعی نرمال است که با $$ \Phi$$ یا $$\text{norm} (x)$$ در زبان‌های نرم‌افزاری بیان می‌شود و تنها در مقیاس‌بندی و تفسیر با آن تفاوت دارد. در واقع:

$$ \large \Phi ( x ) = \frac { 1 } { \sqrt { 2 \pi } } \int _ { - \infty } ^ x e ^ \tfrac { - t ^ 2 } { 2 } \, d t = \frac { 1 } { 2} \left [ 1 + \operatorname {erf} \left ( \frac { x } { \sqrt { 2 } } \right ) \right ] = \frac { 1 } { 2 } \operatorname {erfc} \left ( -\frac { x } { \sqrt { 2 } } \right ) $$

یا برحسب توابع erf و erfc به صورت زیر است:

$$ \large \begin {align}
\operatorname {erf} ( x ) & = 2 \Phi \left ( x \sqrt { 2 } \right ) - 1 \\
\operatorname {erfc} ( x ) & = 2 \Phi \left ( - x \sqrt { 2 } \right ) = 2 \left ( 1 - \Phi \left ( x \sqrt { 2 } \right ) \right ) .
\end {align} $$

در نتیجه، تابع خطا با تابع Q ارتباط دارد که دنباله احتمال توزیع نرمال استاندارد است. تابع Q را می‌توان برحسب توابع خطا به صورت زیر نوشت:

$$ \large Q ( x ) = \frac { 1 } { 2 } - \frac { 1 } { 2 } \operatorname {erf} \left ( \frac { x } { \sqrt { 2 } } \right ) = \frac { 1 } { 2 } \operatorname {erfc} \left ( \frac { x } { \sqrt { 2 } } \right ) . $$

معکوس $$\Phi$$ به عنوان تابع چندک (Quantile) یا تابع پروبیت (Probit) شناخته می‌شود و می‌توان آن را برحسب تابع خطای معکوس به صورت زیر توصیف کرد:

$$ \large \operatorname {probit} ( p ) = \Phi ^ { - 1 } ( p ) = \sqrt { 2 } \operatorname {erf} ^ { - 1 } ( 2 p - 1 ) = -\sqrt { 2 } \operatorname {erfc} ^ { - 1 } ( 2 p ) . $$

تابع توزیع نرمال استاندارد اغلب در آمار و احتمال مورد استفاده قرار می‌گیرد. این در حالی است که تابع خطا، در سایر شاخه‌های ریاضیات استفاده می‌شود.

تابع خطا حالت خاصی از تابع میتاگ-لفر (Mittag-Leffler Function) است. همچنین می‌توان آن را با یک تابع کومر (Kummer's Function) بیان کرد:‌

$$ \large \operatorname {erf} ( x ) = \frac { 2 x } { \sqrt { \pi } } M \left ( \frac 1 2 , \frac 3 2 , - x ^ 2 \right ) . $$

این تابع، بیان ساده‌ای برحسب انتگرال فرینل (Fresnel Integral) دارد.

اگر از تابع گامای ناکامل P استفاده کنیم، داریم:

$$ \large \operatorname {erf} ( x ) = \text{sgn} ( x ) P \left ( \frac 1 2 , x ^ 2 \right ) = \frac { \text{sgn} ( x ) }{ \sqrt { \pi } } \gamma \left ( \frac 1 2 , x ^ 2 \right ) . $$

توابع خطای تعمیم‌یافته

توابع عمومی‌تر خطا را به صورت زیر تعریف شده‌اند:

$$ \large E _ n ( x ) = \frac { n ! } { \sqrt { \pi } } \int _ 0 ^ x e ^ { - t ^ n } \, d t = \frac { n ! }{ \sqrt { \pi } } \sum _ { p = 0 } ^ \infty ( - 1 ) ^ p \frac { x ^ { n p + 1 } } { ( n p + 1 ) p ! } . $$

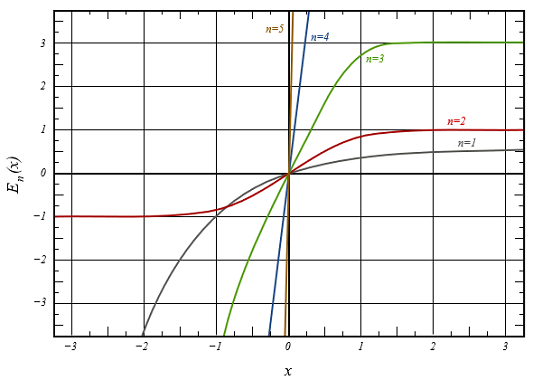
که برخی حالت‌های خاص آن به صورت زیر هستند:

• $$ E_ 0 ( x) $$ خط راستی است که از مبدأ می‌گذرد: $$E_0 ( x) = \frac { x } { e \sqrt{\pi}}$$.
• $$E_ 2 ( x) $$ تابع خطا است: $$\text{erf}(x)$$.

بعد از تقسیم بر $$n ! $$، همه $$ E_ n $$ها برای $$n$$ فرد، مشابه به نظر می‌رسند. همه توابع خطای تعمیم‌یافته برای $$ n > 0 $$ در $$ x>0$$ مشابه هستند.

شکل زیر، این موضوع را به خوبی نشان می‌دهد.

این توابع تعمیم‌یافته را می‌توان با تابع گاما و گامای ناکامل بیان کرد:

$$ \large E _ n ( x ) = \frac { 1 } { \sqrt \pi } \Gamma ( n ) \left ( \Gamma \left ( \frac { 1 } { n } \right ) - \Gamma \left ( \frac { 1 } { n } , x ^ n \right ) \right ) , \quad \quad x > 0 . $$

بنابراین، می‌توان تابع خطا را برحسب تابع گامای ناکامل به صورت زیر نوشت:

$$ \large \operatorname {erf} ( x ) = 1 - \frac { 1 }{ \sqrt \pi } \Gamma \left ( \frac { 1 } { 2 } , x ^ 2 \right ) . $$

انتگرال مکرر تابع خطای مکمل

انتگرال مکرر تابع خطای مکمل به صورت زیر تعریف می‌شود:

$$ \large \begin {align}
\operatorname { i ^ { n } erfc } ( z ) & = \int _ z ^ \infty \operatorname { i ^ { n - 1 } erfc } ( \zeta ) \, d \zeta \\
\operatorname { i ^ { 0 } erfc} ( z ) & = \operatorname {erfc} ( z ) \\
\operatorname { i ^ { 1 } erfc } ( z ) & = \operatorname {ierfc} ( z ) = \frac { 1 } { \sqrt \pi } e ^ { - z ^ 2 } - z \operatorname {erfc} ( z ) \\
\operatorname { i ^ { 2 } erfc } ( z ) & = \frac { 1 } { 4 } \left [ \operatorname {erfc} ( z ) - 2 z \operatorname {ierfc} ( z ) \right ] \\
\end {align} $$

فرمول بازگشتی عمومی به صورت زیر است:

$$ \large 2 n \operatorname { i ^ { n } erfc} ( z ) = \operatorname { i ^ { n - 2 } erfc } ( z ) - 2 z \operatorname { i ^ { n - 1 } erfc } ( z ) $$

سری توانی مربوط به این فرمول برابر است با:

$$ \large i ^ n \operatorname {erfc} ( z ) = \sum _ { j = 0 } ^ \infty \frac { ( - z ) ^ j } { 2 ^ { n - j } j ! \Gamma \left ( 1 + \frac { n - j } { 2 } \right ) } $$

ویژگی‌های تقارن این سری به صورت زیر هستند:

$$ \large i ^ { 2 m } \operatorname {erfc} ( - z ) = - i ^ { 2 m } \operatorname {erfc} ( z ) +\sum _ { q = 0 } ^ m \frac { z ^ { 2 q } } { 2 ^ { 2 ( m - q ) - 1 } ( 2 q ) ! ( m - q ) ! } $$

و

$$ \large i ^ { 2 m + 1 } \operatorname {erfc} ( - z ) = i ^ { 2 m + 1 } \operatorname {erfc} ( z ) +\sum _ { q = 0 } ^ m \frac { z ^ { 2 q + 1 } } { 2 ^ { 2 ( m - q ) - 1 } ( 2 q + 1 ) ! ( m - q ) ! } . $$

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار و احتمالات
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های دروس ریاضیات
• آموزش ریاضی عمومی ۲
• فیلتر کالمن — به زبان ساده
• رسم تابع چگالی احتمال دو بعدی با پایتون — راهنمای کاربردی
• انتگرال توابع گنگ — از صفر تا صد

^^