انتگرال گاوسی — از صفر تا صد
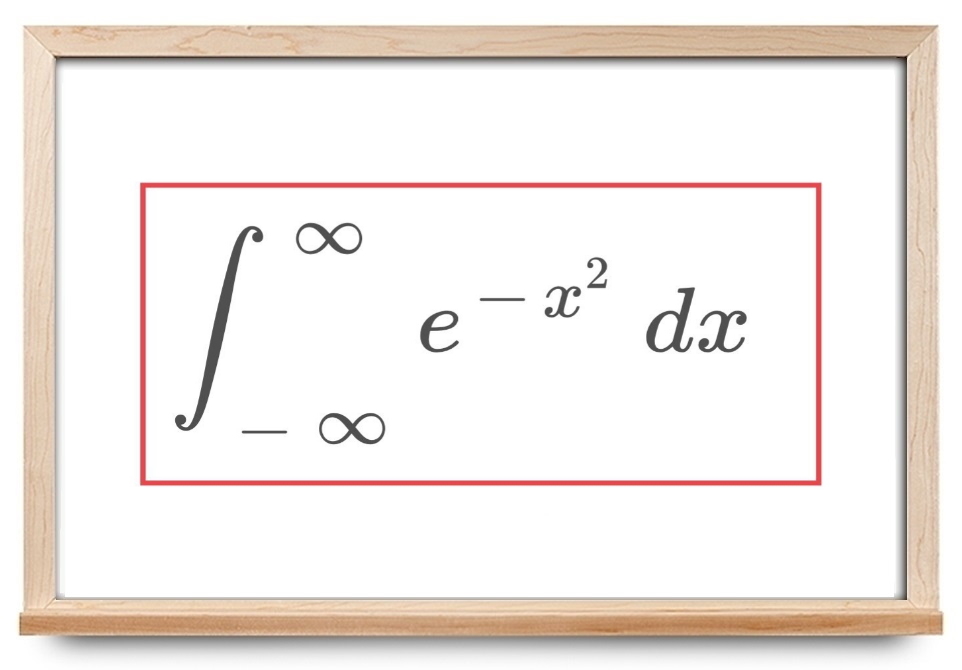
تابع گاوسی $$ f ( x ) = e ^ {-x ^ 2 } $$ یکی از مهمترین توابع در ریاضیات و علوم دیگر است. نمودار زنگولهای شکل این تابع، از توزیع نرمال در آمار تا موقعیت بستههای موج ذره در مکانیک کوانتومی وجود دارد. در این آموزش، با انتگرال گاوسی آشنا میشویم.
انتگرالگیری از توابع گاوسی، یک کار بسیار معمول و رایج است، اما انجام آن با روشهای حسابان مقدماتی کار دشواری است. به عبارت بهتر، با هیچیک از روشهای تغییر متغیر، انتگرالگیری جزء به جزء، جانشینی مثلثاتی و... نمیتوان این انتگرالها را به سادگی محاسبه کرد. در واقع، پادمشتق گاوسی، یعنی تابع خطا (Error Function) را نمیتوان برحسب توابع مقدماتی نوشت. با وجود این، یک جواب دقیق برای انتگرال معین این تابع وجود دارد. در ادامه، روش محاسبه انتگرال گاوسی را بیان میکنیم.
انتگرال گاوسی
در این بخش، طی چند مرحله، انتگرال تابع گاوسی را محاسبه میکنیم:
$$ \large \int _ { - \infty } ^ { \infty } e ^ { - x ^ 2 } \, d x $$
انتگرال را به صفحه $$ x y $$ گسترش میدهیم. دلیل این امر آن است که میخواهیم مسئله را به حل یک انتگرال دوگانه تبدیل کنیم که به آسانی قابل حل است. بنابراین، انتگرال را به صورت زیر نوشته و در پایان، از آن جذر میگیریم:
$$ \large \left ( \int _ { - \infty } ^ { \infty } e ^ { -x ^ 2 } \, d x \right ) ^ 2 = \int _ { - \infty } ^ { \infty } e ^ { - x ^ 2 } \, d x \int _ { - \infty } ^ { \infty } e ^ { - y ^ 2 } \, d y $$
در انتگرال بالا، برای سادهسازی میتوانیم از رابطه $$ r ^ 2 = x ^ 2 + y ^ 2 $$ استفاده کنیم. همانطور که میدانیم، انتگرال سطحی یک مستطیل قطبی به فرم $$ r d r d \theta $$ است که در آن، $$ r$$ برای تطابق مقیاس زاویه با طولها است. این $$r$$ انتگرال را بسیار ساده میکند. بنابراین، انتگرال را به صورت زیر مینویسیم (برای مطالعه بیشتر، میتوانید به آموزش انتگرال در مختصات قطبی مراجعه کنید):
$$ \large \begin {align*} \int _ { - \infty } ^ { \infty } e ^ { - x ^ 2 } \, d x \int _ { - \infty } ^ { \infty } e ^ { - y ^ 2 } \, d y & = \int _ { - \infty } ^ {\infty} d x \int _ { - \infty } ^ { \infty } \, \, d y e ^ { -( x ^ 2 + y^ 2 ) } \\ &=
\int _ { 0 } ^ { \infty } r \, d r \int _ { 0 } ^ { 2 \pi } \; d \theta e ^ { - r ^ 2 } \end {align*} $$
اکنون از تغییر متغیر $$ u = r ^ 2 $$ استفاده میکنیم. در نتیجه، دیفرانسیل $$ d u = 2 r dr $$ را خواهیم داشت. از آنجایی که انتگرالده به $$ \theta $$ وابسته نیست، میتوانیم مقدار انتگرال $$ \theta $$ را سریعاً محاسبه کنیم:
$$ \large \begin {align*} \int _ { 0 } ^ { \infty } r \, d r \int _ { 0 } ^ { 2 \pi } d \theta e ^ { - r ^ 2 } & = 2 \pi \int _ { 0 } ^ {\infty } r e ^ {- r ^ 2 } d r , \; \; \; u = r ^ 2 \\ &=
\pi \int _ { 0 } ^ { \infty } e ^ {-u} d u \\
& = \pi (-e ^ {- \infty } + e ^ 0 ) \\ & = \pi \end {align*} $$
از آنجایی که مقدارِ به دست آمده برای مجذور انتگرال گاوسی است، باید از آن جذر بگیریم. بنابراین، داریم:
$$ \large \int _ { -\infty } ^ { \infty } e ^ {-x ^ 2} dx = \sqrt {\pi} $$
یکی از ویژگیهای مهم تابع گوسی، زوج بودن آن است. در نتیجه، میتوان نوشت:
$$ \large \int _ { -\infty } ^ { \infty } e ^ {-x ^ 2} dx = 2 \int _ { 0 } ^ { \infty } e ^ {-x ^ 2} dx = 2 \cdot \frac { \sqrt {\pi}}{2} $$
انتگرال تابع گاوسی عمومی
تابع گاوسی عمومی با پارامترهای $$a$$ و $$ \sigma$$ تعیین میشود که $$ a $$ یک ثابت (بهنجارش) است و ارتفاع منحنی زنگولهای را مشخص میکند. همچنین، $$ \sigma $$ انحراف معیار است که پهنای منحنی را نشان میدهد:
$$ \large f ( x ) = a e ^ {- \frac { x ^ 2 } { 2 \sigma ^ 2 } } $$
با طی فرایندی مشابه مراحل بالا، میتوان نشان داد که انتگرال تابع گاوسی عمومی به صورت زیر است:
$$ \large \int _ { -\infty } ^ { \infty } a e ^ {- \frac {-x ^ 2}{ 2 \sigma ^ 2} } dx = a \sigma \sqrt {2 \pi} $$
یک راه دیگر برای فرمولبندی مسئله، این است که اگر یک گاوسی به فرم $$ e ^ {- \alpha x ^ 2 } $$ داشته باشیم، انتگرال آن به صورت زیر خواهد بود:
$$ \large \int _ { -\infty } ^ { \infty } e ^ {{- \alpha x ^ 2} } dx = \sqrt \frac {\pi} { \alpha } $$
در بسیاری از کاربردها، لازم است که مساحت گاوسی را برابر با ۱ قرار دهیم. در این حالت، $$ a \sigma \sqrt { 2 \pi} = 1$$ و آن را برای $$ a $$ حل میکنیم:
$$ \large a = \frac { 1 } { \sigma \sqrt {2 \pi}} $$
عبارت بالا، گاوسیِ نرمال شده است و در بسیاری از کاربردها مانند نظریه احتمال و مکانیکی کوانتومی کاربرد دارد:
$$ \large f ( x ) = \frac { 1 } { \sigma \sqrt {2 \pi} } e ^ {{- \frac {x ^ 2 } { 2 \sigma ^ 2 }}} $$
فرمولهای انتگرال توابع گاوسی
در این بخش، فهرستی از انتگرالهایی را بیان میکنیم که کاربردهای فراوانی در مسائل مختلف دارند.
در این انتگرالها که در ادامه میآیند، تابع توزیع نرمال چگالی احتمال به صورت زیر است:
$$ \large \phi = \frac { 1 } { \sqrt { 2 \pi} } e ^ {- \frac {1} { 2} x ^ 2 } $$
همچنین، تابع زیر، تابع توزیع تجمعی مربوط به آن است:
$$ \large \Phi ( x ) = \int _ { – \infty} ^ x \phi ( t ) d t = \frac 1 2 \big ( 1 + \operatorname {erf} \big ( \frac { x }{ \sqrt { 2 } } \big ) \big ) $$
که در آن $$\text{erf}$$، تابع خطا و $$ T ( h , a ) = \phi ( h ) \int _ 0 ^ a \frac { \phi ( h x ) } { 1 +x ^ 2 } \, d x $$ است.
انتگرالهای نامعین
در فرمولهای زیر، $$!!$$ فاکتوریل دوگانه را نشان میدهد.
$$ \large \int \phi ( x ) \, d x = \Phi ( x ) + C $$
$$ \large \int x \phi ( x ) \, d x = - \phi ( x ) + C $$
$$ \large \int x ^ 2 \phi ( x ) \, d x = \Phi ( x ) - x \phi ( x ) + C $$
$$ \large \int x ^ { 2 k + 1 } \phi ( x ) \, d x = -\phi ( x ) \sum _ { j = 0 } ^ k \frac { ( 2 k ) ! ! } { ( 2 j ) ! ! } x ^ { 2 j } + C $$
$$ \large \int x ^ { 2 k + 2 } \phi ( x ) \, d x = -\phi ( x ) \sum _ { j = 0 } ^ k \frac { ( 2 k + 1 ) ! ! } { ( 2 j + 1 ) ! ! } x ^ { 2 j + 1 } + ( 2 k + 1 ) ! ! \, \Phi ( x ) + C $$
$$ \large \int \phi ( x ) ^ 2 \, d x = \frac { 1 } { 2 \sqrt { \pi } } \Phi \left ( x \sqrt { 2 } \right ) + C $$
$$ \large \int \phi ( x ) \phi ( a + b x ) \, d x = \frac { 1 } { t } \phi \left ( \frac { a } { t } \right ) \Phi \left ( t x + \frac { a b }{ t } \right ) + C , \qquad t = \sqrt { 1 + b ^ 2 } $$
$$ \large \int x \phi ( a + b x ) \, d x = - \frac { 1 }{ b ^ 2 } \left ( \phi ( a + b x ) + a \Phi ( a + b x ) \right ) + C $$
$$ \large \int x ^ 2 \phi ( a + b x ) \, d x = \frac { 1 } { b ^ 3 } \left ( ( a ^ 2 + 1 ) \Phi ( a + b x ) + ( a - b x ) \phi ( a + b x ) \right ) + C $$
$$ \large \int \phi ( a + b x ) ^ n \, d x = \frac { 1 } { b \sqrt { n ( 2 \pi ) ^ { n - 1 } } } \Phi \left ( \sqrt { n } ( a +b x ) \right ) + C $$
$$ \large \int \Phi ( a + b x ) \, d x = \frac { 1 } { b } \left ( ( a + b x ) \Phi ( a + b x ) + \phi ( a + b x ) \right ) + C $$
$$ \large \int x \Phi ( a + b x ) \, d x = \frac { 1 }{ 2 b ^ 2 } \left ( ( b ^ 2 x ^ 2 - a ^ 2 - 1 ) \Phi ( a + b x ) + ( b x -a ) \phi ( a + b x ) \right ) + C $$
$$ \large \int x ^ 2 \Phi ( a + b x ) \, d x = \frac { 1 } { 3 b ^ 3 } \left ( ( b ^ 3 x ^ 3 + a ^ 3 + 3 a ) \Phi ( a + b x ) + ( b ^ 2 x ^ 2 - a b x + a ^ 2 + 2 ) \phi ( a + b x ) \right ) + C $$
$$ \large \int x ^ n \Phi ( x ) \, d x = \frac { 1 } { n + 1 } \left ( \left ( x ^ { n + 1 } - n x ^ { n - 1 } \right ) \Phi ( x ) + x ^ n \phi ( x ) + n ( n - 1 ) \int x ^ { n - 2 } \Phi ( x ) \, d x \right ) + C $$
$$ \large \int x \phi ( x ) \Phi ( a + b x ) \, d x = \frac { b } { t } \phi \left ( \frac { a } { t } \right ) \Phi \left ( x t + \frac { a b } { t } \right ) - \phi ( x ) \Phi ( a + b x ) + C , \qquad t = \sqrt { 1 + b ^ 2 } $$
$$ \large \int \Phi ( x ) ^ 2 \, d x = x \Phi ( x ) ^ 2 + 2 \Phi ( x ) \phi ( x ) - \frac { 1 }{ \sqrt { \pi } } \Phi \left ( x \sqrt { 2 } \right ) + C $$
$$ \large \int e ^ { c x } \phi ( b x ) ^ n \, d x = \frac { e ^ { \frac { c ^ 2 } { 2 n b ^ 2 } } } { b \sqrt { n ( 2 \pi ) ^ { n - 1 } } } \Phi \left ( \frac { b ^ 2 x n -c } { b \sqrt { n } } \right ) + C , \qquad b \ne 0 , n > 0 $$
انتگرالهای معین
$$ \large \int _ { - \infty } ^ \infty x ^ 2 \phi ( x ) ^ n \, d x = \frac { 1 } { \sqrt { n ^ 3 ( 2 \pi ) ^ { n - 1 } } } $$
$$ \large \int _ { - \infty } ^ 0 \phi ( a x ) \Phi ( b x ) d x = \frac { 1 } { 2 \pi | a | } \left ( \frac { \pi } { 2 } -\arctan \left ( \frac { b } { | a | } \right ) \right ) $$
$$ \large \int _ 0 ^ { \infty } \phi ( a x ) \Phi ( b x ) \, d x = \frac { 1 } { 2 \pi | a | } \left ( \frac { \pi } { 2 } + \arctan \left ( \frac { b } { | a | } \right ) \right ) $$
$$ \large \int _ 0 ^ \infty x \phi ( x ) \Phi ( b x ) \, d x = \frac { 1 } { 2 \sqrt { 2 \pi } } \left ( 1 + \frac { b } { \sqrt { 1 + b ^ 2 } } \right ) $$
$$ \large \int _ 0 ^ \infty x ^ 2 \phi ( x ) \Phi ( b x ) \, d x = \frac { 1 } { 4 } + \frac { 1 } { 2 \pi } \left ( \frac { b } { 1 + b ^ 2 } + \arctan ( b ) \right ) $$
$$ \large \int _ 0 ^ \infty x \phi ( x ) ^ 2 \Phi ( x ) \, d x = \frac { 1 } { 4 \pi \sqrt { 3 } } $$
$$ \large \int _ 0 ^ \infty \Phi ( b x ) ^ 2 \phi ( x ) \, d x = \frac { 1 } { 2 \pi } \left ( \arctan ( b ) + \arctan \sqrt { 1 + 2 b ^ 2 } \right ) $$
$$ \large \int _ { - \infty } ^ \infty \Phi ( a + b x ) ^ 2 \phi ( x ) \, d x = \Phi \left ( \frac { a } { \sqrt { 1 + b ^ 2 } } \right ) - 2 T \left ( \frac { a } { \sqrt { 1 + b ^ 2 } } , \frac { 1 }{ \sqrt { 1 + 2 b ^ 2 } } \right ) $$
$$ \large \int _ { - \infty } ^ { \infty } x \Phi ( a + b x ) ^ 2 \phi ( x ) \, d x = \frac { 2 b } { \sqrt { 1 + b ^ 2 } } \phi \left ( \frac { a } { t } \right ) \Phi \left ( \frac { a }{ \sqrt { 1 + b ^ 2 } \sqrt { 1 + 2 b ^ 2 } } \right ) $$
$$ \large \int _ { - \infty } ^ \infty \Phi ( b x ) ^ 2 \phi ( x ) \, d x = \frac { 1 } { \pi } \arctan \sqrt { 1 + 2 b ^ 2 } $$
$$ \large \int _ { - \infty } ^ \infty x \phi ( x ) \Phi ( b x ) \, d x = \int _ { - \infty } ^ \infty x \phi ( x ) \Phi ( b x ) ^ 2 \, d x = \frac { b } { \sqrt { 2 \pi ( 1 + b ^ 2 ) } } $$
$$ \large \int _ { - \infty } ^ \infty \Phi ( a + b x ) \phi ( x ) \, d x = \Phi \left ( \frac { a } { \sqrt { 1 + b ^ 2 } } \right ) $$
$$ \large \int _ { - \infty } ^ \infty x \Phi ( a + b x ) \phi ( x ) \, d x = \frac { b } { t } \phi \left ( \frac { a } { t } \right ) , \qquad t = \sqrt { 1 + b ^ 2 } $$
$$ \large \int _ 0 ^ \infty x \Phi ( a + b x ) \phi ( x ) \, d x = \frac { b } { t } \phi \left ( \frac { a } { t } \right ) \Phi \left ( -\frac { a b } { t } \right ) + \frac { 1 } { \sqrt { 2 \pi } } \Phi ( a ) , \qquad t = \sqrt { 1 + b ^ 2 } $$
$$ \large \int _ { - \infty } ^ \infty \ln ( x ^ 2 ) \frac { 1 } { \sigma } \phi \left ( \frac { x } { \sigma } \right ) \, d x = \ln ( \sigma ^ 2 ) - \gamma - \ln 2 \approx \ln ( \sigma ^ 2 ) - 1.27036 $$
اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:
- آموزش ریاضی عمومی ۲
- فیلتر کالمن — به زبان ساده
- رسم تابع چگالی احتمال دو بعدی با پایتون — راهنمای کاربردی
- انتگرال توابع گنگ — از صفر تا صد
^^











عالی
سلام این تابع در این بخش به خوبی و خلاصه معرفی شده