معادلات تابعی — به زبان ساده

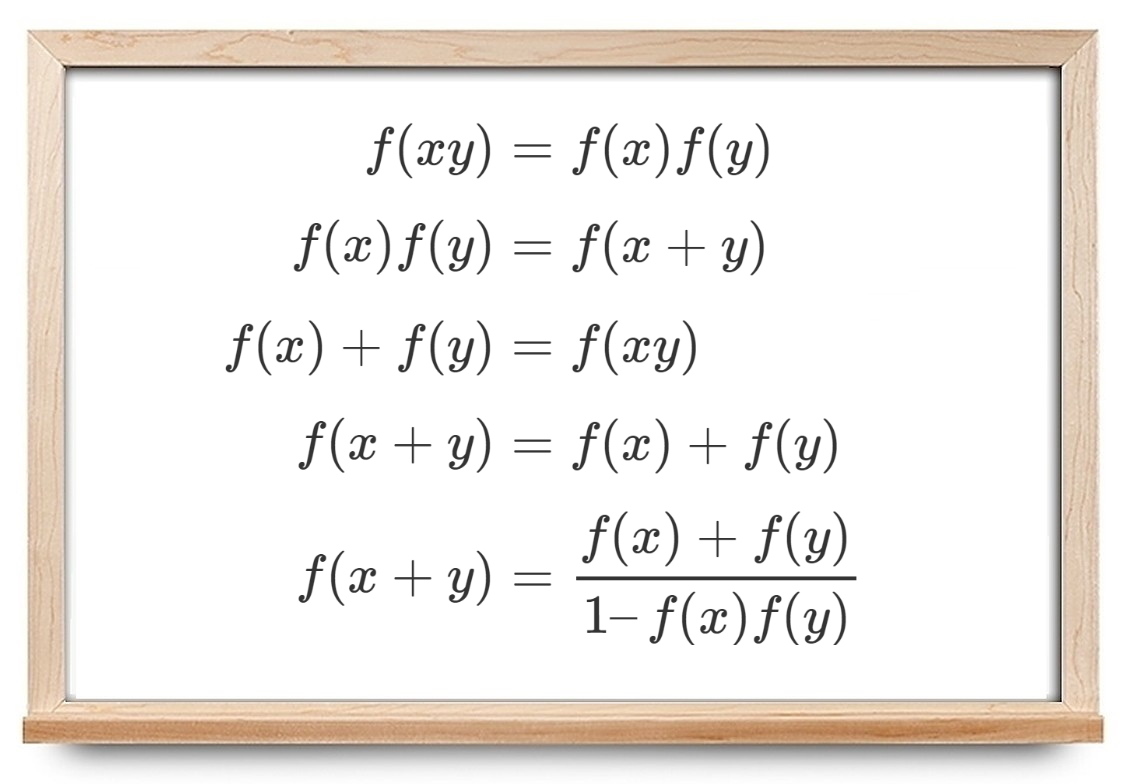
«معادلات تابعی« (Functional Equations) معادلاتی هستد که مجهول‌ آن‌ها به جای متغیرهای معمولی، تابع است. با این حال، روش‌های مورد استفاده برای حل معادلات تابعی ممکن است کاملاً متفاوت با روش‌های حل معادلات متغیری باشد. معادلات تابعی اطلاعاتی درباره یک تابع یا چند تابع ارائه می‌کنند. برای مثال، $$ f ( x ) - f ( y ) = x - y $$ یک معادله تابعی است. در اینجا، $$ f $$ یک تابع است و می‌بینیم که اختلاف بین هر دو خروجی برابر با اختلاف بین دو مقدار ورودی است. تابع $$ f ( x ) = x $$ و به طور عمومی‌تر، $$ f ( x ) = x + c $$ برای هر عدد ثابت $$ c $$ در معادله تابعی بالا صدق می‌کند.

آشنایی با معادلات تابعی

سعی کنید یک جواب (نه لزوماً همه جواب‌های) معادلات تابعی زیر را حدس بزنید.

• ۱) $$ f(xy)=f(x)f(y) $$
• ۲) $$f(x)f(y)=f(x+y) $$
• ۳) $$f(x)+f(y)=f(xy) $$
• ۴) $$f(x+y)=f(x)+f(y) $$
• ۵) $$ f ( x + y ) = \frac { f ( x ) + f ( y ) } { 1 - f ( x ) f ( y ) } $$

اولین معادله ما را به یاد تابع $$ f ( x ) = x ^ s $$ می‌اندازد. معادله تابعی دوم تابع نمایی، یعنی $$ f ( x ) = e ^ x $$ را تداعی می‌کند که در آن، $$ e $$ یک مقدار معلوم است. سومی تابع لگاریتمی را یادآوی می‌کند. چهارمی یک معادله تابعی مشهور به نام معادله تابعی کوشی است و تابع $$ f ( x ) = c x $$ را یادآوری می‌کند. در نهایت، آخرین مورد مشابه تابع تانژانت است.

توجه کنید که لزومی ندارد هیچ‌یک از توابع بالا توابعی باشند که با آن‌ها آشنایی داریم و مشخص هستند. همچنین، توجه به این نکته ضروری است که اگر بخواهیم توابع بالا جواب مسئله باشند، باید فرض کنیم پیوسته هستند. مثلاً‌ $$ f ( x y ) = f ( x ) f ( y ) $$ را درنظر بگیرید که دارای جواب $$ f ( 0 ) = 0 $$ و $$ f ( x ) = 1 $$ (برای $$x \neq 0 $$) است. با وجود این، بسیار مهم است که توابع متداول را تشخیص دهیم. اما این نکته هم وجود دارد که رایج‌ترین و ساده‌ترین جواب‌ها لزوماً جواب معادله نیستند.

دو مورد مهم که در مثال‌های فوق دامنه و دامنه مشترک توابع است. ما فرض کردیم که این توابع برای اعداد حقیقی تعریف شده‌اند و به خروجی‌های حقیقی می‌انجامند، اما این موضوع لزوماً اتفاق نمی‌افتد. دامنه و دامنه مشترک اساساً می‌تواند هر چیزی باشد که می‌خواهید، و به دلیل تغییر دامنه و دامنه مشترک ممکن است تابع تغییر کند.

در مثال‌های بالا، سه مورد رایج را می‌بینیم که در مسائل معادلات تابعی وجود دارند:

• دامنه و دامنه مشترک
• مقدار $$ f $$ در برخی مقادیر
• معادله (معادلات) تابعی اصلی

مثال‌هایی از معادلات تابعی

در این بخش، چند مثال از معادلات تابعی را بررسی می‌کنیم.

مثال اول معادلات تابعی

اگر $$ f ( x + 3 ) = x ^ 2 + 8 x + 1 6 $$ باشد، آنگاه مقدار $$ f ( x ) $$ چقدر است؟

پاسخ: با در نظر گرفتن $$ y = x + 3 $$، خواهیم داشت: $$ x = y - 3 $$. با جایگذاری این عبارت در $$ f ( x + 3 ) = x ^ 2 + 8 x + 16 $$، به $$ f ( y) = y ^ 2 + 2 y + 1 $$ خواهیم رسید. در نتیجه، $$ f ( x ) = x ^ 2 + 2 x + 1 = ( x + 1 ) ^ 2 $$ است.

مثال دوم معادلات تابعی

$$ f $$ تابعی است که در ۳ شرط زیر صدق می‌کند:

• $$ f:\mathbb{N}\rightarrow \mathbb{N} $$
• $$ \sqrt{f(x)}\ge \frac{f(1)+f(x)}{2} $$ برای مقادیر دامنه $$ x $$
• $$ \frac { f ( n ) } { f ( 1 ) } = 2 n - \big ( f ( 1 ) \big ) ^ 2 , \ n \ge 2 $$.

همه این توابع را بیابید.

پاسخ: شرایط را تک به تک بررسی می‌کنیم. اولین مورد اساساً می‌گوید که این تابع فقط مقادیر صحیح مثبت را می‌پذیرد و همیشه اعداد صحیح مثبت را نتیجه خواهد داد. مورد دوم باید نابرابری میانگین حسابی هندسی را یادآوری می‌کند. $$ x $$ را یک عدد صحیح مثبت در نظر بگیرید که به ازای آن، تساوی برقرار است. با استفاده از میانگین حساب هندسی، خواهیم داشت:

$$ \large \sqrt { f ( x ) } \ge \dfrac { f ( 1 ) + f ( x ) } { 2 } \ge \sqrt { f ( x ) f ( 1 ) } . $$

اما از آنجا که $$ f \ge 1 $$، است، داریم: $$ \sqrt { f ( x ) } \le \sqrt { f ( x ) f ( 1 ) } $$. بنابراین، نامساوی‌های بالا دقیقاً تساوی هستند. در نتیجه، برای آنکه تساوی برقرار باشد، باید $$ f ( 1 ) = 1 $$ را داشته باشیم. با جایگذاری این عبارت در شرط سوم، برای همه $$ n \ge 2 $$، خوهیم داشت: $$ f ( n ) = 2 n - 1 $$. در نهایت، $$ f ( 1 ) = 2 \cdot 1 - 1 $$ را داریم. بنابراین، تابع $$ f ( n ) = 2 n - 1 $$ است که برای همه $$n$$ها برقرار است.

مثال سوم معادلات تابعی

برای تابع $$ f ( x ) = 10 ^ { 2 x }  + 10 ^ x + 1 $$، مقدار $$ \displaystyle \sum _ { x = 1 } ^ { n } ( x - 1 ) f ( \log _ { 1 0 } x ) $$ را محاسبه کنید.

پاسخ: در واقع، آن چیزی که باید پیدا کنیم، $$ f ( \log _ {10} x) $$ است. بدین منظور، که به سادگی می‌توان نوشت:

$$ \large \begin {aligned} f ( x ) & = 1 0 ^ { 2 x } + 1 0 ^ x + 1 \\ f ( \log _ { 1 0 } x ) & = 1 0 ^ { 2 \log _ { 1 0 } x } + 1 0 ^ { \log _ { 1 0 } x } + 1 . \end {aligned} $$

با تعریف $$ a ^ { \log _ a x } = x $$، داریم:

$$ \large \begin {aligned} f ( \log _ { 1 0 } x ) & = x ^ 2 + x + 1 \\ ( x - 1 ) f ( \log _ { 1 0 } x ) & = ( x - 1 ) ( x ^ 2 + x + 1 ) \\ & = x ^ 3 - 1 . \end {aligned} $$

این مسئه اکنون به محاسبه عبارت زیر کاهش می‌یابد:

$$ \large \sum _ { x = 1 } ^ { n } ( x ^ 3 - 1 ) = \left ( \dfrac { n ( n + 1 ) } { 2 } \right ) ^ 2 - n $$

حل معادلات تابعی با تغییر متغیر

هنگام کار با معادلات تابعی، یکی از اولین کارهایی که باید انجام دهیم، تغییر متغیرها در تابع است. این کار معمولاً با دو هدف انجام می‌شود: یکی برای بررسی رفتار تابع و دیگری رسیدن به یک معادله مناسب است. اغلب موارد، تغییر مقادیر ساده‌ای مانند $$ 1$$، $$ 0 $$، $$ - 1 $$ و $$ - y $$ می‌تواند به حل مسئله کمک کند.

مثال اول حل معادلات تابعی با تغییر متغیر

اگر $$ f ( x + 3 ) = x ^ 2 + 8 x + 1 6 $$ باشد، مقدار $$ f ( x ) $$ را به دست آورید.

پاسخ: در اینجا، یک تغییر متغیر مناسب $$ x $$ را انجام می‌دهیم تا مقدار $$ f ( x ) $$ را به دست آوریم. توجه کنید که از قبل می‌دانیم مقدار $$ f ( x + 3 ) $$ چقدر است. اکنون باید از خودمان بپرسیم: «چه چیزی را می‌توانیم به جای $$ x $$ قرار دهیم تا $$ x $$ را از $$ x + 3 $$ به دست آوریم؟» البته که به سادگی می‌توانیم $$ x - 3 $$ را به جای $$ x $$ قرار دهیم. در این صورت، $$ x + 3 $$ به $$ ( x - 3 ) + 3 = x $$ تبدیل می‌شود که کارساز خواهد بود، زیرا در این صورت، داریم:

$$ \large f \big ( ( x - 3 ) + 3 \big ) = f ( x ) =(x-3)^2+8(x-3)+16=x^2+2x+1 $$

این همان چیزی است که به دنبال آن بودیم.

شاید تغییر متغیر در همه موارد به راحتی امکان پذیر نباشد. بنابراین یک راه بهتر، انجام مواردی است که در مثال‌های بعدی به آن‌ها اشاره می‌کنیم.

مثال دوم حل معادلات تابعی با تغییر متغیر

اگر $$ f ( x + 3 ) = x ^ 2 + 8 x + 16 $$ باشد، آنگاه مقدار $$ f( x ) $$ را به دست آورید.

پاسخ: $$ y= x + 3 $$ را در نظر بگیرید. در نتیجه، $$ x = y - 3 $$ خواهد بود. اکنون $$ x = y - 3 $$ را در $$ f ( x + 3 ) = x ^ 2 + 8 x + 16 $$ قرار می‌دهیم تا $$ f ( y) = y ^ 2 + 2 y + 1 $$ به دست آید و در نتیجه، $$ f ( x ) = x ^ 2 + 2 x + 1 = ( x + 1 ) ^ 2 $$ خواهد بود.

مثال بالا یک کاربرد ساده از تغییر متغیر است. این ساده‌ترین حالتی است که در آن از تغییر متغیر استفاده می‌شود.

مثال زیر کاربرد «توابع چرخه‌ای» (Cyclic Functions)‌ را در حل معادلات تابعی نشان می‌دهد که در ادامه به آن‌ها خواهیم پرداخت.

مثال سوم حل معادلات تابعی با تغییر متغیر

همه توابع $$ f : \mathbb { R } - \{ 0 \} \longrightarrow \mathbb { R }$$ را که در معادله زیر صدق می‌کنند، به دست آورید:

$$ \large f ( x ) + 3 f \left ( \frac { 1 } { x } \right ) = x ^ 2 . $$

پاسخ: $$ x $$ و $$ \frac { 1 } { x } $$ را در این مثال مشاهده می‌کنیم. اگر $$ \frac {1}{ x } $$ را به جای $$ x $$ قرار دهیم، خواهیم داشت:

$$ \large \begin {aligned} f \left ( \frac { 1 } { x } \right ) + 3 f \left ( \frac { 1 } { \frac 1 x } \right ) & = \frac { 1 } { x ^ 2 } \\ f \left ( \frac { 1 } { x } \right ) + 3 f ( x ) & = \frac { 1 }{ x ^ 2 } . \end {aligned} $$

اکنون یک معادله جدید داریم. با مقایسه معادله جدید با معادله قبلی، داریم:

$$ \large \begin {aligned} f ( x ) + 3 f \left ( \frac { 1 } { x } \right ) & = x ^ 2 \\ f \left ( \frac { 1 } { x } \right ) + 3 f ( x ) & = \frac { 1 } { x ^ 2 } \end {aligned} $$

مشاهده می‌کنید که یک دستگاه معادلات داریم و باید آن را برای $$ f ( X ) $$ حل کنیم. بنابراین، با در نظر گرفتن $$ f ( x ) $$ و $$ f ( \frac { 1 } { x } )$$ به عنوان متغیرها، عبارت $$ f ( x ) $$ را به دست می‌آوریم. جواب آخر برابر است با:

$$ \large - \frac { x ^ 2 } { 8 } + \frac { 3 } { 8 x ^ 2 } . $$

به خاطر داشته باشید که $$ \frac{1}{\frac {1}{x}} = x $$. بنابراین، وقتی این تغییر متغیر را انجام دادیم، معادله دیگری با همان متغیرها خواهیم داشت. در نتیجه، می‌توانیم دستگاه معادلات خطی را به راحتی حل کنیم. این مثال دو مورد را یادآوری می‌کند:

• استفاده از توابع چرخه‌ای (در ادامه، درباره این توابع بحث خواهیم کرد).
• تغییر متغیر می‌تواند به یک دستگاه معادلات خطی (یا درجه بالاتر) بینجامد که می‌توانیم از آن استفاده کنیم و تابع را به دست آوریم. این مورد ابزار بسیار مفیدی برای حل معادلات تابعی است.

قبل از اینکه مثال‌های بیشتری حل کنیم، کمی در مورد توابع چرخه‌ای بحث می‌کنیم.

حل معادلات تابعی با توابع چرخه‌ای

یک تابع، چرخه‌ای با مرتبه $$ n $$ است اگر برای هر $$ x $$، داشته باشیم: $$ f \Big ( f \big (... f ( x ) ...\big ) \Big ) = x $$. در اینجا، $$ f $$ به تعداد $$ n $$ بار رخ می‌دهد. اگر دقت کنید، $$ g ( x ) = \frac { 1 } { x } $$ یک تابع چرخه‌ای با مرتبه $$ 2 $$ است، زیرا $$ g (g (x)) = x $$.

تابع $$ f ( x ) = 1 - x $$ نیز یک تابع چرخه‌ای با مرتبه $$ 2 $$ است، زیرا $$ f ( f ( x )) = f ( 1 - x ) = 1 - (1 - x ) = x $$.

یک کاغذ را روی میز در نظر بگیرید. تابع $$ f $$ را تعریف می‌کنیم. آنچه این تابع هر بار انجام می‌دهد، این است که کاغذ را به اندازه $$ 60 ^ \circ $$ می‌چرخاند. بنابراین، بعد از شش بار اعمال این تابع، کاغذ به اندازه $$ 360 ^ \circ $$ خواهد چرخید و به موقعیت اولیه خود بر خواهد گشت. بنابراین، $$ f $$ چرخه‌ای با مرتبه $$ 6 $$ است، زیرا با شش بار اعمال تابع، به آنچه خواهیم رسید که در موقعیت اولیه داشتیم.

اکنون به مبحث معادلات تابعی و کاربرد توابع چرخه‌ای در آن‌ها می‌پردازیم. در مثال بالا عبارت $$ \frac { 1 } { x } $$ را در تابع داشتیم و می‌دانیم که یک تابع چرخه‌ای با مرتبه دو است. بنابراین، وقتی $$ x $$ را به جای $$ \frac { 1 } { x } $$ قرار می‌دهیم، موقعیت جملات $$ f ( x ) $$ و $$ f ( \frac { 1 } { x } ) $$ تغییر می‌کند و منجر به یک دستگاه معادلات خطی ساده می‌شود. در ادامه، چند مثال از کاربرد توابع چرخه‌ای در حل معادلات تابعی را بررسی می‌کنیم.

مثال اول حل معادلات تابعی با توابع چرخه‌ای

همه توابع تعریف شده در مجموعه اعداد حقیقی را بیابید که در معادله تابعی $$ f ( x ) + 2 f ( 1 - x ) = x ^ 3 $$ صدق می‌کنند.

پاسخ: همان‌طور که پیش‌تر گفتیم، $$ 1 - x $$ چرخه‌ای با مرتبه دو است. بنابراین، اگر $$ x $$ را به جای $$ 1 - x $$ قرار دهیم، جملات $$ f ( x ) $$ و $$ f ( 1 - x ) $$ جایگزین خواهند شد و دوباره یک دستگاه معادلات خطی داریم. سعی کنید خودتان تابع را از آن به دست آورید.

اما مشابه سایر موارد، گاهی کشف برخی توابع چرخه‌ای دشوار است. وقتی نمی‌توانیم راه‌حل مسائل را سریعاً تشخیص دهیم، باید مقادیر حقیقی را به عنوان ورودی وارد کرده و مقادیر $$ f $$ را محاسبه کنیم. این موضوع به ما دید بهتری خواهد داد. مثال زیر مرتبط با این موضوع است.

مثال دوم حل معادلات تابعی با توابع چرخه‌ای

همه توابع $$ f $$ بیابید که در معادله تابعی زیر هسنند:

$$ \large \begin {array} { c } & f : \mathbb { R } - \{ 0 , 1 \} \longrightarrow \mathbb { R } , & f ( x ) + f \left ( \dfrac { 1 } { 1 - x } \right ) = 1 + \dfrac { 1 } { x ( 1 - x ) } . \end {array} $$

پاسخ: از آنجا که احتمالاً نمی‌توانیم مستقیماً بررسی کنیم $$ \frac { 1 } { 1 - x } $$ دوره‌ای با مرتبه ۳ است، از یک روش کمی متفاوت‌تر استفاده می‌کنیم. مقادیر را جایگذاری می‌کنیم.

در اینجا $$ x = - 1 $$ بهترین انتخاب است و خواهیم داشت:

$$ \large f ( - 1 ) + f \left ( \frac 1 2 \right ) = \text {something} . $$

اکنون، از آنجا که $$ \frac 12 $$ را در $$ f $$ داریم، می‌توانیم $$ x = \frac 12 $$ را قرار دهیم و داشته باشیم:

$$ \large f \left ( \frac 1 2 \right ) + f ( 2 ) = \text {something} $$

و در نهایت، از آنجا که $$ 2 $$ درون $$ f $$ است، آن را جایگذاری می‌کنیم و داریم:

$$ \large f ( 2 ) + f ( - 1 ) = \text {something} . $$

اکنون به سادگی یک دستگاه معادلات خطی شامل سه معادله و سه مجهول داریم و می‌توانیم به سادگی مقادیر آن‌ها را بیابیم.

باید این موضوع را بررسی کنید که آیا $$ \frac { 1 } { 1 - x } $$ واقعاً دوره‌ای است یا خیر. پاسخ این پرسش به راحتی ما را به راه‌حل سوق می‌دهد.

معادلات تابعی دو متغیره

هنگام استفاده از تغییر متغیر در یک معادله تابعی با چند متغیر، یک نکته مهم وجود دارد که باید به دنبال آن باشیم. این موضوع در واقع در هر شاخه ریاضی مطرح می‌شود و تقارن نام دارد. گاهی می‌توان از ایده استاندارد زیر در مورد تقارن استفاده کرد.

در یک معادله تابعی دو متغیره، اگر عبارت یک طرف نسبت به متغیرها متقارن باشد، در حالی که در سمت دیگر تقارن وجود نداشته باشد، استفاده از تغییر متغیر $$ (m , n ) \to ( n , m ) $$ ایده خوبی خواهد بود.

گفته بالا اساساً‌ بیان می‌کند که مکان متغیرها را تغییر دهیم. این موضوع را با یک مثال بیان می‌کنیم.

مثال اول حل معادلات تابعی دو متغیره

همه توابع $$ f : \mathbb { N } \rightarrow \mathbb { N } $$ را به گونه‌ای بیابید که در معادله زیر صدق کنند:

$$ \large \begin {array} { c } & f \big ( f ( m ) + f ( n ) \big ) = f \big ( f ( m ) \big ) + f ( n ) , & f ( 1 ) = 2 , & f ( 2) = 4 . \end {array} $$

پاسخ: رابطه زیر را داریم:

$$ \large f \big ( f ( m ) + f ( n ) \big ) = f \big ( f ( m ) \big ) + f ( n ) . \qquad ( 1 ) $$

می‌بینیم که سمت چپ با توجه به متغیرها متقارن است، در حالی که در سمت راست چنین نیست. ار تغییر متغیر $$ ( m , n ) \to ( 1 , n ) $$ استفاده می‌کنیم و خواهیم داشت:

$$ \large f \big ( f ( 1 ) + f ( n ) \big ) = f \big ( f ( 1 ) \big ) + f( n ) . $$

اکنون جای $$ m $$ و $$ n $$ را تعویض می‌کنیم:

$$ \large f \big ( f ( n ) + f ( 1 ) \big ) = f \big ( f ( n ) \big ) + f ( 1 ) . $$

شاید این پرسش برایتان ایجاد شده باشد که چگونه بفهمیم $$ 1 $$ را در یکی از متغیرها قرار دهیم. ما نمی‌دانیم، اما در واقعیت، ابتدا تغییر متغیر $$ ( m , n ) = ( n , m ) $$ را انجام می‌دهیم و سپس قرار دادن $$ 1 $$ به ما کمک می‌کند. به هر صورت، با استفاده از دو معادله، داریم:

$$ \large \begin {aligned} f \big ( f( 1 ) \big ) + f ( n ) & = f \big ( f ( n ) \big ) +f (1 ) \\ f \big ( f ( n ) \big ) & = f ( n ) + 2 \end {aligned} $$

زیرا مقادیر $$ f ( 1 ) $$ و $$ f ( 2 ) $$ در مثال داده شده‌اند. اکنون، می‌بینیم که $$ f ( n ) = m $$ منجر به $$ f ( m ) = m + 2 $$ خواهد شد. با استفاده از استقرا، می‌توان $$ f ( m + 2 k ) = m + 2 k + 2 $$ را اثبات کرد، که در آن، $$ k \ge 0 $$ است. اکنون از تغییر متغیر $$m=2n$$ استفاده می‌کنیم و برای همه اعداد صحیح مثبت، $$ f ( 2 n ) = 2 n + 2 $$ را خواهیم داشت.

اکنون خاصیت یک به یک بودن $$ f $$ این امکان را می‌دهد که بتوانیم بگوییم $$ f $$ مقادیر فرد را به ازای ورودی‌های فرد نتیجه می‌دهد (به جز $$ 1 $$ که خروجی آن، $$ 2 $$ می‌شود). اگر $$ f ( t ) $$ برای برخی از $$ t $$ها برابر با $$ f ( t) = 1 $$ باشد، آنگاه از تغییر متغیر $$ m = t$$ و $$ n = t $$ در $$ ( 1 ) $$ استفاده می‌کنیم. این، به یک تناقض واضح می‌انجامد.

مجدداً فرض کنید برای برخی $$ t $$ها، مقدار $$ f ( t ) = 3 $$ را داشته باشیم. در نتیجه، $$ f ( 3 + 2 k ) = f \big ( f ( t ) + 2 k \big ) = f (t ) + 2 k + 2=5+2k $$ را داریم که یک تناقض است، زیرا برای $$ k \ge 0 $$ هیچ ورودی نمی‌تواند خروجی $$ 3 $$ را داشته باشد.

فرض کنید $$ p $$ کوچک‌ترین عدد صحیح مثبتی باشد که برای برخی $$k$$ها، تساوی $$ f ( k) = 2 p + 1 $$ را داشته باشیم. در نتیجه، برای $$ s \ge 0 $$، خواهیم داشت: $$ f ( 2 p + 2 s + 1 ) = 2 p + 2 s + 3 $$. این رابطه نتیجه می‌دهد که $$ 3 $$، $$ 5 $$، $$ 7 $$، ... و $$ 2 p - 1 $$ به $$ 5$$، $$ 7 $$، ... و $$ 2 p + 1 $$ تصویر می‌شوند. بنابراین، $$ f ( 3 + 2 k) = 5 + 2 k $$.

در نهایت، می‌توان نتیجه گرفت که تابع برابر است با:

$$ \large f ( 1 ) = 2 , \;\;\; f ( n ) = n + 2 , \; \; n \ge 2 . $$

مثال دوم حل معادلات تابعی دو متغیره

همه توابع $$ f : \mathbb { R } \rightarrow \mathbb { R } $$ را به گونه‌ای بیابید که داشته باشیم:

$$ \large f ( x + y ) - f ( x - y ) = f ( x ) f ( y ) . $$

پاسخ: می‌بینیم که سمت راست معادله تابعی نسبت به متغیرها متقارن است، اما سمت چپ آن این‌گونه نیست. بنابراین، از تغییر متغیر $$ x = y $$ و $$ y = x $$ استفاده می‌کنیم:

$$ \large f ( y + x ) - f ( y - x) = f ( y ) f ( x ) . $$

در نتیجه، می‌توان تساوی $$ f ( x - y ) = f ( y - x ) $$ را نتیجه گرفت که معادل با $$ f ( a ) = f ( - a ) $$ است. اکنون از تغییر متغیر $$ y \to - y $$ استفاده می‌کنیم و خواهیم داشت:

$$ \large f ( x - y ) - f ( x + y ) = f ( x ) f ( - y ) . $$

مشاهده می‌کنیم که سمت چپ معادله بالا همان سمت چپ معادله اصلی است که در $$ - 1 $$ ضرب شده است. سمت راست معادله بالا $$ f ( x ) f ( - y ) = f ( x) f ( y ) $$ است، زیرا $$ f (y ) = f ( - y ) $$. بنابراین، از آنجا که سمت راست و چپ برابرند، برای همه زوج مرتب‌های حقیقی، داریم:

$$ \large - f ( x ) f ( y ) = f ( x ) f ( y ) $$

در نتیجه، $$ f $$ باید $$ 0 $$ باشد.

در ادامه، مثال دیگری را بررسی می‌کنیم که در آن، دو متغیر وجود دارد، اما تابع کمی متفاوت است. هرگاه توابع $$ f : \mathbb { R } ^ 2 \rightarrow \mathbb { R } $$ را دیدیم، همان تغییر متغیرهایی را استفاده می‌کنیم که در مثال‌های بالا اعمال کردیم. بدین ترتیب، به سادگی جای $$ x $$ و $$ y $$ را تعویض می‌کنیم.

مثال سوم حل معادلات تابعی دو متغیره

تابع $$ f : \mathbb { R } ^ 2 - \{ ( 1 , 1 ) \} \longrightarrow \mathbb { R } $$ را بیابید که به صورت زیر تعریف شده است:

$$ \large f ( x , y ) = x + y f ( y , x ) . $$

پاسخ: تغییر متغیر $$ ( x , y ) \rightarrow ( y , x ) $$ مناسب به نظر می‌رسد و در نتیجه آن، خواهیم داشت:

$$ \large f ( y ,x ) = y + x f ( x , y ) . $$

اکنون با در نظر گرفتن $$ f ( x , y ) $$ و $$ f ( y , x ) $$ به عنوان متغیر، می‌توانیم آن‌ها را به دست آوریم. محاسبه آن‌ها کار ساده‌ای است که به عنوان تمرین خودتان می‌توانید آن را انجام دهید.

مثال چهارم حل معادلات تابعی دو متغیره

همه توابع $$ f $$ را در صورتی به دست آورید که داشته باشیم:

$$ \large f : \mathbb { Q } \longrightarrow \mathbb { Q } , \ f ( 1 ) = 2 , \ f ( x y ) = f ( x ) f ( y ) - f ( x + y ) + 1 . $$

پاسخ: $$ y = 1 $$ را در معادله قرار می‌دهیم و برای همه اعداد گویای $$ x $$، تساوی $$ f ( x ) = 2 f ( x ) - f ( x + 1 ) + 1 $$ یا $$ f ( x + 1 ) - f ( x ) = 1 $$ را خواهیم داشت. از آنجا که $$ f ( 1 ) = 2 $$ است، قطعاً به ازای همه اعداد صحیح $$ n $$ در $$ f ( n ) = n +  1 $$ صدق می‌کند. با قرار دادن $$ y = n $$ در معادله داده شده، که $$ n $$ یک عدد صحیح مثبت است، برای همه اعداد گویای $$ x $$ خواهیم داشت:

$$ \large f ( n x ) \; = \; f ( x ) f ( n ) - f ( x + n ) + 1 \; = \; ( n + 1 ) f ( x ) - \big ( f ( x ) + n \big ) + 1 \; = \; n f ( x ) - n + 1 $$

و در نتیجه، برای هر $$ m $$ و $$ n $$ با $$ n > 0$$، می‌توان نوشت:

$$ \large m + 1 \; = \; f ( m ) \; = \; f \big ( n \tfrac { m } { n } \big ) \; = \; n f \big ( \tfrac { m } { n } \big ) - n + 1 $$

که برای همه $$ x $$های گویا، $$ f \big ( \tfrac { m } { n } \big ) = \tfrac { m } { n } + 1 $$ و در نتیجه، $$ f ( x ) = x + 1 $$ از آن استنباط می‌شود. برای این معادله تابعی تنها یک جواب وجود دارد.