مدولاسیون فرکانس — از صفر تا صد
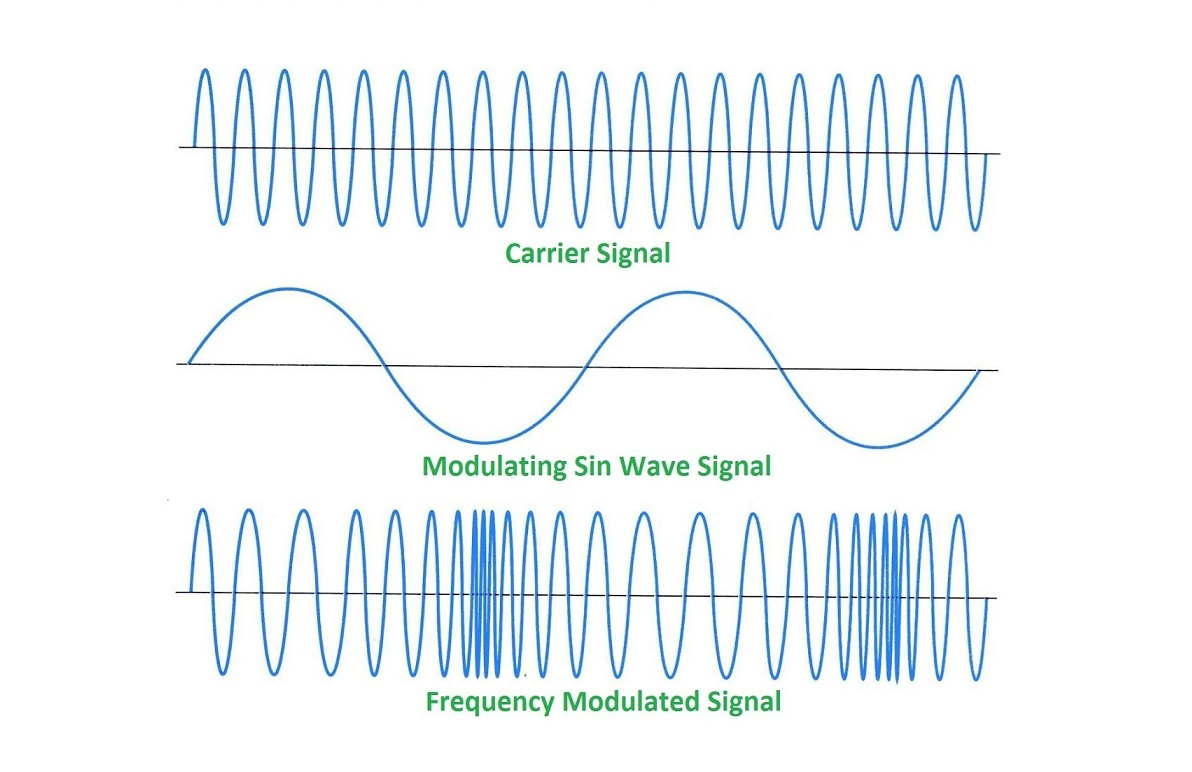
مدولاسیون فرکانس (Frequency Modulation) یا FM مبحثی بسیار مهم در علم مخابرات و پردازش سیگنال است که به فرآیند کدگذاری اطلاعات موجود در سیگنال پیام از طریق تغییر فرکانس لحظهای موج حامل اطلاق میشود. در این مقاله قصد داریم به بررسی مدولاسیون فرکانس بپردازیم و با تئوری و نحوه پیادهسازی و کاربردهای این نوع از مدولاسیون آشنا شویم.
در مقالات پیشین مجله فرادرس به توضیح اهمیت مدولاسیون و نیز معرفی این تکنیک پرداختیم. دادههای دیجیتال میتوانند از طریق مدولاسیون فرکانس نیز کدگذاری شده و سپس به مسافتهای طولانی ارسال شوند. در واقع این کار از طریق انتقال (Shift) فرکانس سیگنال حامل در میان مجموعهای از پیشتعیین شده از فرکانسها انجام میگیرد، به صورتی که هر فرکانس، نشاندهنده عدد خاصی در داده دیجیتالی است. به عنوان مثال، یک فرکانس میتواند نشاندهنده عدد یک باینری و فرکانس دیگری میتواند نشاندهنده عدد صفر باینری باشد. این تکنیک مدولاسیون، کلیدزنی انتقال فرکانسی (Frequency-Shift Keying) نام دارد و به اختصار FSK گفته میشود. FSK به صورت گسترده در مودمهایی مانند فکس مودمها (Fax Modem) مورد استفاده قرار میگیرد. همچنین برای ارسال کد مورس و در رادیو تله تایپ (Radioteletype) نیز میتوان از FSK استفاده کرد.
مدولاسیون فرکانس عمدتا برای انتشار رادیویی FM مورد استفاده قرار میگیرد. از این نوع مدولاسیون همچنین در کاربردهایی مانند اندازهگیری از راه دور (Telemetry)، رادار، کاوش زمین لرزه، پایش وضعیت سلامت نوزادان تازه به دنیا آمده برای جلوگیری از تشنج (با استفاده از سیگنالهای EEG)، سیستمهای رادیویی دو طرفه، آنالیز موسیقی، سیستم ضبط نوار مغناطیسی و برخی سیستمهای انتقال ویدیویی استفاده میشود.
در ارتباطات رادیویی، یکی از مزیتهای اصلی مدولاسیون فرکانسی این است که دارای نسبت سیگنال به نویز بسیار بزرگی است و بنابراین قادر خواهد بود تداخلات فرکانس رادیویی را بهتر از یک سیگنال مدولاسیون دامنه با توان برابر رد (Reject) کند. به همین دلیل است که امروزه اکثرا سیگنال موسیقی را با استفاده از مدولاسیون فرکانس منتشر میکنند.
مدولاسیون فرکانس و مدولاسیون فاز دو روش اصلی و مکمل در گروه مدولاسیون زاویه (Angle Modulation) هستند. مدولاسیون فاز معمولا به عنوان یک گام میانی برای رسیدن به مدولاسیون فرکانس محسوب میشود. این روش بر خلاف مدولاسیون دامنه عمل میکند. در تکنیک مدولاسیون دامنه، دامنه سیگنال حامل تغییر میکند اما فرکانس و فاز آن ثابت باقی میمانند. در انیمیشن زیر نمایی از خروجیهای مدولاسیون دامنه و فاز را میتوان مشاهده کرد.
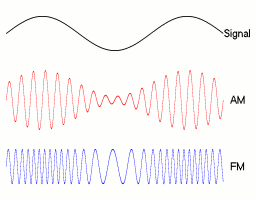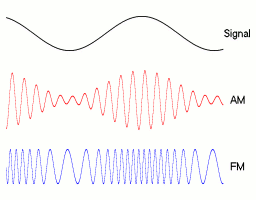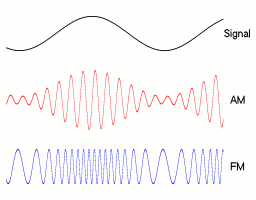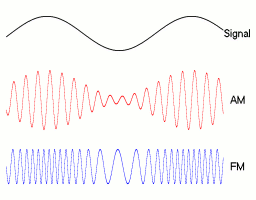
در مدولاسیون فرکانس آنالوگ، انحراف فرکانسی (Frequency Deviation) لحظهای عبارت است از اختلاف بین فرکانس سیگنال حامل و فرکانس مرکزی آن و این مقدار متناسب با سیگنال مدولاسیون است. انتشار رادیویی یک سیگنال صوتی (حاوی گفتار یا موزیک) با مدولاسیون فرکانس، نمونهای از مدولاسیون FM آنالوگ است.
ریاضیات مدولاسیون فرکانس
سیگنال پیامی که قرار است منتقل شوند را $$ x(m(t) $$ فرض کرده و سیگنال حامل سینوسی را با معادله زیر نشان میدهیم:
$$ x_c(t) = A_c \cos (2 \pi f_c t) $$
در فرمول بالا، $$ f_c $$ فرکانس پایه سیگنال حامل و $$ A_c $$ دامنه سیگنال حامل است. مدولاسیون فرکانس، سیگنال حامل را با سیگنال پیام باند پایه (Baseband Data Signal) ترکیب میکند و در نهایت سیگنال مدولاسیون به صورت زیر به دست میآید که قابل انتقال تا مسافتهای طولانی است.
$$ y(t) = A_c \cos (2 \pi \int_{0}^{t} f(\tau) d\tau) \\
= A_c \cos (2 \pi \int_{0}^{t} [f_c + f_\triangle x_m (\tau)] d\tau) \\
= A_c \cos ( 2 \pi f_c t + 2 \pi f_ \triangle \int_{0}^{t} x_m (\tau) d\tau) $$
در فرمول بالا، $$ f_\triangle = k_f A_m $$ است که در آن $$ k_f $$ حساسیت مدولاتور فرکانس و $$ A_m $$ دامنه سیگنال پیام یا سیگنال باند پایه را نشان میدهد. در این معادله $$ f_\tau $$، فرکانس لحظهای اسیلاتور و $$ f_\triangle $$ انحراف فرکانسی است. انحراف فرکانسی نشاندهنده بیشینه انتقال نسبت به $$ f_c $$ در یک جهت است، با این فرض که $$ x_m(t) $$ در بازه $$ \pm 1 $$ محدود باشد.
نمایی از سیگنال پیام، سیگنال حامل و سیگنال مدوله شده توسط مدولاسیون فرکانس در تصویر زیر نشان داده شدهاند.
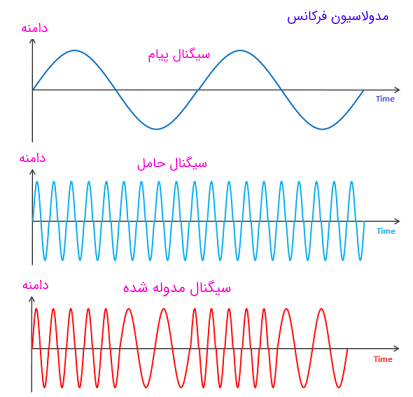
به دلیل اینکه قسمت عمده انرژی سیگنال در $$ f_c \pm f_\triangle $$ است، از طریق آنالیز فوریه میتوان نشان داد که گستره وسیعی از فرکانسها مورد نیاز است تا بتوان یک سیگنال FM را با دقت بالا نمایش داد. طیف فرکانسی متعلق به یک سیگنال FM واقعی، دارای المانهایی است که تا بینهایت بسط داده شدهاند، البته دامنه این المانها به تدریج کاهش مییابند و از المانهای مراتب بالا معمولا در مسائل طراحی عملی صرف نظر میشود. در تصویر زیر نمایی از طیف فرکانسی متعلق به یک سیگنال FM نشان داده شده است.
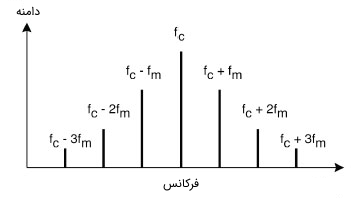
سیگنال باند پایه سینوسی
از لحاظ ریاضی، سیگنال پیام باند پایه را میتوان با موج پیوسته سینوسی تقریب زد که دارای فرکانس $$ f_m $$ باشد. این روش، مدولاسیون تک تن (Single-Tone Modulation) نیز نامیده میشود. انتگرال چنین سیستمی برابر است با:
$$ \int_{0}^{t} x_m (\tau) d\tau = A_m \frac { \sin ( 2 \pi f_m t)} {2 \pi f_m} $$
در این حالت، میتوان معادله $$ y(t) $$ به دست آمده در قسمت قبل را به صورت زیر بازنویسی کرد:
$$ y(t) = A_c \cos (2 \pi f_c t + \frac {A_m f_\triangle} {f_m } \sin (2 \pi f_m t)) $$
در این فرمول، دامنه $$ A_m $$ سیگنال سینوسی باند پایه، توسط انحراف $$ f_\triangle $$ نمایش داده میشود. توزیع هارمونیک سیگنال حامل سینوسی که توسط چنین سیگنال باند پایه سینوسی مدوله شده باشد را میتوان با استفاده از توابع بسل (Bessel Functions) نمایش داد. این امکان، پایهای برای درک ریاضیات مدولاسیون فرکانس در حوزه فرکانس (Frequency Domain) را فراهم میآورد.
شاخص مدولاسیون فرکانس
همانند سایر سیستمهای مدولاسیون، شاخص مدولاسیون (Modulation Index) در مدولاسیون فرکانس نشان میدهد که سیگنال مدوله شده تا چه مقدار حول سطح مدوله نشده خود تغییر کرده است. شاخص مدولاسیون به تغییر در فرکانس سیگنال حامل وابسته است. در نتیجه میتوان فرمول شاخص مدولاسیون فرکانس را به صورت زیر نوشت:
$$ h = \frac {\triangle f} {f_m} = \frac {f_\triangle |x_m (t)|} {f_m} $$
در این فرمول، $$ f_m $$ بزرگترین المان فرکانس حاضر در سیگنال پیام $$ x_m(t) $$ و $$ \triangle f $$ پیک انحراف فرکانسی یا به عبارت دیگر، بیشینه انحراف فرکانس لحظهای از فرکانس حامل در نظر گرفته میشوند. بنابراین برای یک مدولاسیون سینوسی، شاخص مدولاسیون را میتوان به صورت نسبت پیک انحراف فرکانسی موج حامل بر فرکانس سیگنال پیام سینوسی در نظر گرفت.
مدولاسیون باند باریک
اگر $$ h \ll 1 $$ باشد، آنگاه چنین مدولاسیونی را مدولاسیون باند باریک FM یا Narrowband FM میگویند. در این حالت پهنای باند مدولاسیون فرکانس تقریبا $$ 2f_m $$ خواهد بود. اکثرا شاخص مدولاسیون $$ h < 0.3 $$ را مدولاسیون باند باریک یا NFM محسوب کرده و سایر موارد را مدولاسیون فرکانس پهن باند (Wideband FM) یا WFM در نظر میگیرند.
در سیستمهای مدولاسیون دیجیتال مانند کلیدزنی شیفت فرکانسی باینری (Binary Frequency Shift Keying) یا BFSK، یک سیگنال باینری موج حامل را مدوله میکنیم. در این سیستمها شاخص مدولاسیون توسط فرمول زیر محاسبه میشود:
$$ h = \frac {\triangle f} {f_m} = \frac {\triangle f} {\frac {1} {2T_s}} = 2 \triangle f T_s $$
در این فرمول، $$ T_s $$ به صورت قراردادی نماد دوره تناوب و $$ f_m = \frac {1} {2T_s} $$ به عنوان بزرگترین فرکانس موج پیام باینری مورد استفاده قرار میگیرد، اگرچه شاید دقیقتر باشد که بگوییم $$ f_m = \frac {1} {2T_s} $$ بزرگترین پایه (Fundamental) شکل موج پیام باینری است. در مورد مدولاسیون دیجیتال، فرکانس حامل $$ f_c $$ هرگز منتقل نمیشود. در عوض یکی از دو فرکانس $$ f_c + \triangle f $$ یا $$ f_c - \triangle f $$ ارسال میشوند که به حالت باینری ۰ یا ۱ در سیگنال پیام بستگی دارد. نمایی از سیگنالها در مدولاسیون دیجیتال کلیدزنی شیفت فرکانسی باینری در تصویر زیر دیده میشود.
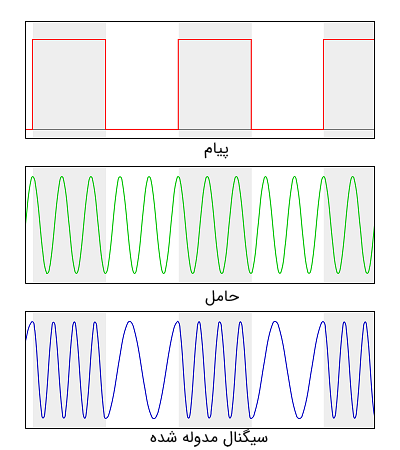
مدولاسیون پهن باند
اگر $$ h \gg 1 $$ باشد، مدولاسیون فرکانس را پهن باند یا WFM میگویند. در این صورت پهنای باند تقریبا برابر با $$ 2 f_\triangle $$ در نظر گرفته میشود. اگرچه مدولاسیون پهن باند، پهنای باند بیشتری را اشغال میکند، اما میتواند نسبت سیگنال به نویز را بهبود ببخشد. به عنوان مثال، با دو برابر کردن مقدار $$ \triangle f $$، در حالی که $$ f_m $$ ثابت باشد، نسبت سیگنال به نویز به اندازه هشت برابر بهبود مییابد.
در یک موج FM تک تن، اگر فرکانس مدولاسیون ثابت نگه داشته شود و شاخص مدولاسیون افزایش یابد، آنگاه پهنای باند سیگنال FM افزایش مییابد، اما فضای بین طیف همچنان ثابت باقی میماند. در این حالت، شدت برخی از عناصر طیفی کاهش و برخی افزایش مییابند. اگر انحراف فرکانسی ثابت نگه داشته شود و فرکانس مدولاسیون افزایش داده شود، آنگاه فضای بین طیف افزایش مییابد.
اگر تغییر در فرکانس حامل مشابه با فرکانس پیام باشد، آنگاه مدولاسیون فرکانس را میتوان جزو مدولاسیون باند باریک طبقهبندی کرد. همچنین اگر تغییر در فرکانس حامل بسیار بالاتر از فرکانس سیگنال پیام (شاخص مدولاسیون > ۱) باشد، مدولاسیون را میتوان به عنوان پهن باند طبقهبندی کرد. مدولاسیون باند باریک، به عنوان مثال در ارتباطات رادیویی دو طرفه کاربرد دارد که در این ارتباطات سیگنال حامل فقط اجازه دارد در حدود ۲٫۵ کیلو هرتز بالا و پایین فرکانس مرکزی منحرف شود. بنابراین سیگنالهای حرف زدن نمیتوانند پهنای باند بیشتر از ۳٫۵ کیلو هرتز داشته باشند. مدولاسیون فرکانس پهن باند برای انتشار FM مورد استفاده قرار میگیرد که در آن موسیقی و کلام با انحراف بالاتر از ۷۵ کیلو هرتز از فرکانس مرکزی منتقل میشوند و سیگنال صوت را پهنای باند بیشتر از ۲۰ کیلو هرتز و زیر حامل بالاتر از ۹۲ کیلو هرتز حمل میکند.
توابع بسل
برای مواردی که یک سیگنال حامل توسط یک موج تکی سینوسی مدوله شود، طیف فرکانسی حاصل را میتوان با استفاده از توابع بسل نوع اول به عنوان یک تابع از عدد باند جانبی و شاخص مدولاسیون محاسبه کرد. دامنه سیگنالهای حامل و باند جانبی برای چند مقدار شاخص مدولاسیون متفاوت در سیگنالهای FM به عنوان مثال در جدول زیر محاسبه شدهاند. برای مقادیر خاصی از شاخص مدولاسیون، دامنه موج حامل صفر میشود و تمام توان سیگنال در باندهای جانبی قرار میگیرد.
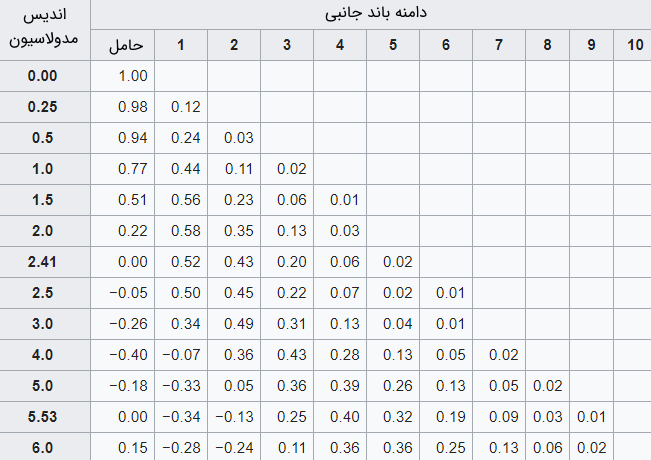
چون باندهای جانبی در هر دو طرف از سیگنال حامل هستند، دو بار حساب میشوند و سپس برای یافتن پهنای باند در فرکانس مدولاسیون ضرب میشوند. به عنوان مثال، انحراف ۳ کیلو هرتز که توسط موج صوتی ۲٫۲ کیلو هرتز مدوله شود، شاخص مدولاسیون در حدود ۱٫۳۶ را تولید میکند. فرض کنید که خود را به تولید باندهای جانبی محدود کنیم که دارای دامنه نسبی حداقل ۰٫۰۱ باشند. بنابراین، با استفاده از جدول بالا میتوان نشان داد که این شاخص مدولاسیون سه باند جانبی را تولید میکند. این سه باند جانبی، پس از دو برابر شدن به ما پهنای باند $$ 6 \times 2.2 KHZ = 13.2 KHZ $$ میدهند.
قاعده کارسون
در سیستمهای مخابراتی با استفاده از قاعده پهنای باند کارلسون (Carson Bandwidth Rule)، پهنای باند تقریبی مورد نیاز در یک سیستم مخابراتی را تعریف میکنند. این پهنای باند متعلق به سیگنال حاملی است که توسط طیف گسترده یا پیوسته فرکانسی، به جای تک فرکانس، مورد مدولاسیون فرکانس قرار گرفته باشد. این قاعده به خوبی بر روی سیگنالهای پیام حاوی ناپیوستگی مانند موج مربعی، قابل اعمال نیست.
بر اساس قاعده ساده کارسون (Carson's Rule)، حدودا تمام (۹۸ درصد) توان سیگنالی که مدولاسیون فرکانس شده باشد، در پهنای باند $$ B_T $$ قرار دارد. این پهنای باند را میتوان به صورت زیر به دست آورد:
$$ B_ T = 2(\triangle f + f_m) = 2 f_m (\beta+1) $$
که در این فرمول، $$ \triangle f $$، همانطور که در بالا اشاره شد، برابر با پیک انحراف فرکانس لحظهای $$ f(t) $$ از فرکانس مرکزی حامل $$ f_c $$ و $$ \beta $$ برابر با شاخص مدولاسیون (نسبت انحراف فرکانس به بالاترین فرکانس در سیگنال پیام) و $$ f_m $$ بالاترین فرکانس در سیگنال پیام است. البته به این نکته توجه کنید که فقط در مورد سیگنالهای سینوسی میتوان از قاعده کارلسون استفاده کرد.
$$ B_ T = 2(\triangle f + W) = 2W (D+1) $$
در فرمول بالا، $$ W $$ برابر با بزرگترین فرکانس در سیگنال پیامی است که دارای طبیعت غیر سینوسی باشد و $$ D $$ نسبت انحراف در نظر گرفته میشود که برابر با نسبت انحراف فرکانسی به بزرگترین فرکانس سیگنال پیام غیر سینوسی است.
کاهش نویز
در قسمتهای قبل هم به این موضوع اشاره شد که در مدولاسیون فرکانس یا FM در مقایسه با مدولاسیون دامنه یا AM، نسبت سیگنال به نویز بهبود یافته است. نسبت به یک مدولاسیون دامنه بهینه، میتوان گفت که مدولاسیون فرکانس به ازای مقادیر زیر یک سطح سیگنال خاص که سطح آستانه نام دارد، دارای نسبت سیگنال به نویز ضعیفتری است. اما به ازای مقادیر بالاتر از یک سطح خاص (که آستانه بهبود کامل (Full Improvement) یا آستانه آرامش کامل (Full Quieting Threshold) نام دارد)، نسبت سیگنال به نویز یا SNR سیگنال مدولاسیون فرکانس در مقایسه با مدولاسیون دامنه، بسیار بهتر است. در واقع بهبود نسبت سیگنال به نویز یا SNR، به انحراف و سطح مدولاسیون بستگی دارد. در تصویر آزمایش انجام شده در سال ۱۹۴۰ در آمریکا را مشاهده میکنید که در آن از یک منبع توان بالا به عنوان نویز در پشت یک رادیو استفاده شده است. رادیو مجهز به گیرنده FM و AM است. در گیرنده AM مقادیر تصادفی به عنوان سیگنال پیام دریافت شده بود در حالیکه در گیرنده FM سیگنال موسیقی با وضوح بالا دریافت شد. این آزمایش تاییدی بر رد نویز بالای مدولاسیون FM است.

برای کانالهای مخابرات صوتی معمولی، میزان بهبود در حدود 5 تا 15 دسی بل است. پخش برنامهها با مدولاسیون فرکانس (FM Broadcasting) و یک انحراف گستردهتر، میتوان SNR را حتی به مقدار بیشتری بهبود داد. تکنیکهای دیگر، مانند فرکانسهای صوتی بالاتر یا پیش متمرکز (Pre-Emphasis)، معمولا برای بهبود SNR کلی در مدارات مدولاسیون فرکانسی مورد استفاده قرار میگیرند. چون سیگنالهای مدولاسیون فرکانس دارای دامنه ثابتی هستند، گیرندههای مدولاسیون فرکانس معمولا قسمتهای محدودکننده (Limiter) دارند تا نویزهای AM را حذف کنند و در نتیجه نسبت سیگنال به نویز را بهبود دهند.
پیادهسازی
سیگنالهای مدولاسیون فرکانس میتوانند توسط مدولاسیون فرکانس مستقیم یا غیر مستقیم تولید شوند. مدولاسیون فرکانس مستقیم (Direct FM Modulation)، از طریق ارسال سیگنال پیام به صورت مستقیم، به ورودی اسیلاتور کنترل شده با ولتاژ (Voltage-Controlled Oscillator) تولید میشود. در تصویر زیر نمایی از یک مدار اسیلاتور کنترل شده با ولتاژ نشان داده شده است.
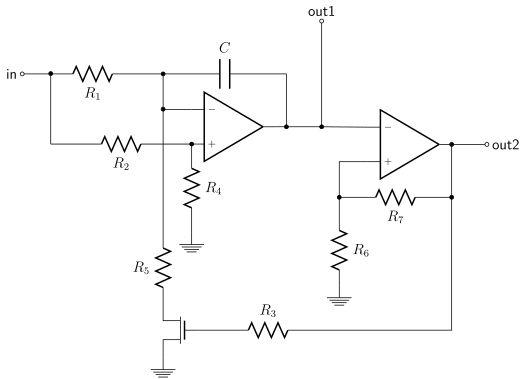
اما در ایجاد مدولاسیون فرکانس غیر مستقیم (Indirect FM Modulation)، از سیگنال پیام برای ایجاد سیگنال فاز مدوله شده، انتگرال (Integrate) گرفته میشود. این تکنیک برای مدولاسیون یک اسیلاتور کنترل شده کریستال (Crystal-Controlled Oscillator) مورد استفاده قرار میگیرد و سپس خروجی حاصل برای تولید سیگنال FM از یک ضرب کننده فرکانسی (Frequency Multiplier) عبور داده میشود. ضرب کننده فرکانسی، یک مداری الکترونیکی است و میتواند سیگنال خروجی را تولید کند که فرکانس آن هارمونیکی از فرکانس ورودی باشد. در این حالت، مدولاسیون فرکانس باند باریک تولید میشود و میتواند در نهایت به مدولاسیون فرکانس پهن باند منجر شود. به همین دلیل این نوع مدولاسیون را با نام مدولاسیون فرکانس غیر مستقیم میشناسند. در تصویر زیر شماتیک یک مدار ضرب کننده فرکانسی را مشاهده میکنید.
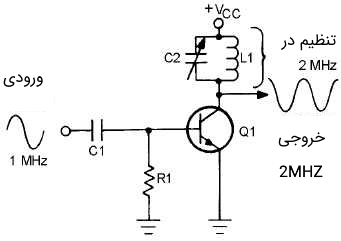
دمدولاسیون
انواع مختلفی از مدارات آشکارساز مدولاسیون فرکانس (FM Detector Circuits) وجود دارند. یک روش متداول برای بازیابی سیگنال اطلاعات از طریق تفکیک کننده فاستر-سیلی (Foster-Seeley Discriminator) یا آشکار ساز نسبت (Ratio Detector) است. یک حلقه قفل فاز (Phase-Locked Loop) نیز میتواند به عنوان یک دمدولاتور FM مورد استفاده قرار گیرد. آشکارسازی شیب (Slope Detection) نیز یک سیگنال FM را دمدوله میکند. این کار با استفاده از یک مدار تنظیم شده انجام میپذیرد که فرکانس رزونانس آن دارای اندکی انحراف از فرکانس حامل باشد. با صعود و نزول فرکانس، مدار تنظیم شده در پاسخ دامنهای متغیر را به وجود میآورد و FM را به AM تبدیل میکند. گیرندههای AM ممکن است برخی از انتقالهای FM را تشخیص دهند، اما ابزاری کارآمد برای آشکارسازی انتشار FM را فراهم نمیکنند. در تصویر زیر نمایی از حلقه قفل فاز نشان داده شده است.
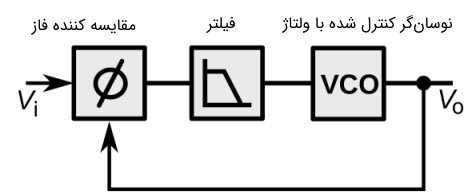
کاربردها
مدولاسیون فرکانس، در فرکانسهای میانی توسط سیستمهای ضبط کننده کاست ویدیویی یا VCR آنالوگ، برای ضبط قسمت سیاه و سفید سیگنالهای ویدیویی مورد استفاده قرار میگیرند. معمولا المان رنگ در این سیگنالها توسط سیگنال مدولاسیون دامنه استاندارد ضبط میشود که از سیگنال FM با فرکانس بالاتر به عنوان بایاس استفاده میکند. FM تنها روش قابل قبول برای ضبط قسمت سیاه و سفید در سیگنال ویدیویی بر روی نوار مغناطیسی بدون اعوجاج است. سیگنالهای ویدیویی گستره وسیعی از فرکانسها، از چند هرتز تا چندین مگا هرتز را شامل میشوند و به همین دلیل برای کار با اکولایزرها (Equalizers) بسیار مناسب هستند. مدولاسیون FM همچنین قادر است نوار را در سطح اشباع نگه دارد و مانند یک سیستم کاهش نویز عمل کند. به صورت خلاصه کاربردهای مدولاسیون فرکانس را میتوان به صورت زیر بیان کرد.
- انتشار FM
- رادار
- سیستمهای ضبط نوار مغناطیسی
- اندازهگیری از راه دور یا تله متری
- سیستمهای رادیویی دو طرفه
- ترکیب (Synthesis) موسیقی
مزایای مدولاسیون فرکانس
- تمام توان منتقل شده در مدولاسیون فرکانس مفید است، در حالیکه در مدولاسیون دامنه قسمت عمده توان در سیگنال حامل قرار دارد که غیر قبال استفاده است.
- در مدولاسیون فرکانس تداخل کانالهای مجاور اتفاق نمیافتد.
- نسبت سیگنال به نویز در مدولاسیون فرکانس بالاتر است. به عبارت دیگر میتوان گفت که نویز کمتری در سیگنال مدولهشده وجود دارد.
- عیب مدولاسیون فرکانس در این است که به پهنای باند بیشتری نسبت به مدولاسیون دامنه نیاز دارد.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای مهندسی مخابرات
- آموزش مخابرات ۱
- مجموعه آموزشهای مهندسی الکترونیک
- آموزش مبانی الکترونیک – مفاهیم تئوریک به همراه شبیه سازی عملی و کاربردی
- دمدولاسیون دامنه — از صفر تا صد
- انرژی و توان سیگنال — از صفر تا صد
- مدولاسیون فاز — راهنمای جامع
^^











سلام
درسته
سلام
من یک سوال داشتم
یک مدار فرستنده و گیرنده مدولاسیون طراحی کردم
می خواستم ببینم درسته یا نه
افرین…درسته مدارت