تابع شبکه و پاسخ فرکانسی – به زبان ساده (+ دانلود فیلم آموزش رایگان)

پاسخ فرکانسی حالت دائمی سینوسی مدار، در موارد مختلفی از جمله سیستم‌های مخابراتی و سیستم‌های کنترل کاربرد فراوانی دارد. به‌طور خاص، یکی از کاربردهای پاسخ فرکانسی در فیلترها است که فرکانس‌های مورد نظر طراحی را عبور داده و سایر فرکانس‌ها را حذف می‌کنند. در این آموزش، ابتدا تابع شبکه را معرفی کرده، سپس با استفاده از آن‌، رسم پاسخ فرکانسی را در قالب نمودارهای بُد بیان خواهیم کرد.

تابع شبکه

تابع تبدیل (Transfer Function) یا تابع شبکه (Network Function) $$\mathbf {H} ( \omega )$$، یک ابزار تحلیلی برای یافتن پاسخ فرکانسی مدار است. در حقیقت، پاسخ فرکانسی یک مدار، نمودار تابع شبکه $$\mathbf {H} ( \omega )$$ براساس $$\omega$$ است که از $$\omega =0$$ تا $$\omega = \infty$$ تغییر می‌کند.

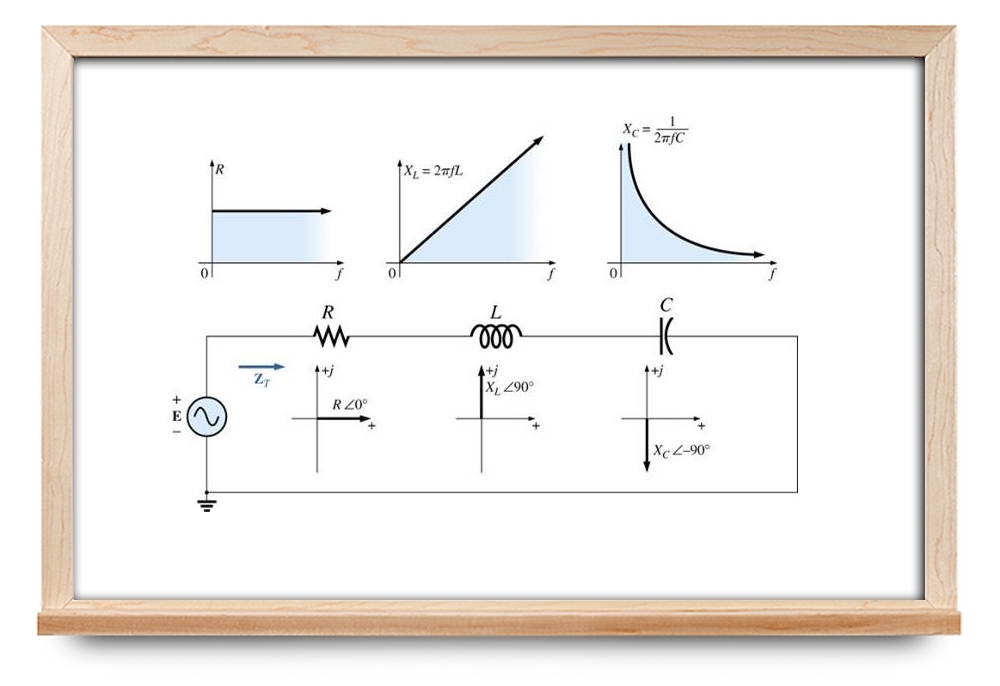
تابع شبکه، نسبت وابسته به فرکانسِ یک تابع خروجی به یک تابع ورودی است. در حالت کلی، یک شبکه خطی را می‌توان مطابق شکل ۱ نمایش داد.

تابع شبکه $$\mathbf {H} ( \omega )$$ مدار، نسبت وابسته به فرکانسِ فازور خروجی $$\mathbf {Y} ( \omega )$$ (ولتاژ یا جریان) به فازور ورودی $$\mathbf {X} ( \omega )$$ (منبع ولتاژ یا جریان) است.

بنابراین، با فرض شرایط اولیه صفر، داریم:

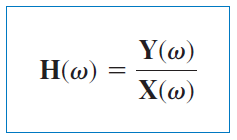
از آن‌جایی که ورودی و خروجی می‌توانند ولتاژ یا جریان هر نقطه‌ای از مدار باشند، چهار تابع شبکه ممکن وجود دارد:

که در آن‌ها، پایین‌نویس‌های $$i$$ و $$o$$ به‌ترتیب، مقادیر ورودی و خروجی را نشان می‌دهند. تابع $$\mathbf {H} ( \omega )$$، مختلط بوده و دارای اندازه $$H ( \omega )$$ و زاویه فاز $$\phi$$ است ($$\mathbf {H} ( \omega ) = H ( \omega ) \angle \phi$$).

برای نوشتن تابع شبکه، ابتدا معادل حوزه فرکانس مدار را با جایگزینی مقاومت‌ها، سلف‌ها و خازن‌ها با امپدانس‌های $$R$$، $$j \omega L$$ و $$1/j \omega C$$ به‌دست می‌آوریم. پس از آن، از یکی از تکنیک‌های تحلیل مدار برای به‌دست آوردن یکی از معادلات (2) استفاده می‌کنیم. پاسخ فرکانسی را می‌توان با رسم اندازه و فاز تابع شبکه برای فرکانس‌های مختلف رسم کرد.

تابع شبکه $$\mathbf {H} ( \omega )$$ با نسبت چندجمله‌ای صورت $$\mathbf {N} ( \omega )$$ و چندجمله‌ای مخرج $$\mathbf {D} ( \omega )$$ قابل بیان است:

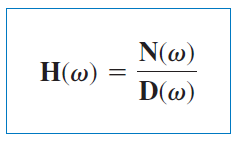
که در آن، $$\mathbf {N} ( \omega )$$ و $$\mathbf {D} ( \omega )$$ لزوماً توصیفات یکسانی برای توابع ورودی و خروجی ندارند.

در نمایش $$\mathbf {H} ( \omega )$$ رابطه (۳) فرض شده که عامل‌های مشترک صورت و مخرج حذف شده‌اند. ریشه‌های $$\mathbf {N} ( \omega ) =0$$، صفرهای $$\mathbf {H} ( \omega )$$ نامیده شده و معمولاً به‌صورت $$j \omega = z_1 , z_2 , \cdots$$ نشان داده می‌شوند. به‌طریق مشابه، ریشه‌های $$\mathbf {D} ( \omega ) =0$$ را قطب‌های $$\mathbf {H} ( \omega )$$ می‌نامند و به‌صورت $$j \omega = p_1 , p_2 , \cdots$$ نشان می‌دهند.

برای اجتناب از انجام عملیات جبری پیچیده، $$j \omega$$‌ را با $$s$$ جایگزین می‌کنیم.

پاسخ فرکانسی

در ادامه، نحوه رسم پاسخ فرکانسی مدار را بررسی می‌کنیم. ابتدا با مقیاس دسی‌بل آشنا می‌شویم.

مقیاس دسی‌بل

رسم سریع اندازه و فاز تابع شبکه، همیشه کار آسانی نیست. یک راه نظام‌مند برای به‌دست آوردن پاسخ فرکانسی، استفاده از «نمودار بُد» (Bode Plot)‌ یا بود یا بودی یا بودا است. قبل از پرداختن به نمودارهای بُد، لازم است با موضوع مهم استفاده از لگاریتم و دسی‌بل برای توصیف بهره آشنا باشیم.

از آن‌جایی که نمودارهای بُد براساس لگاریتم هستند، لازم است روابط زیر را در ذهن داشته باشیم:

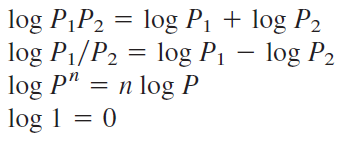
در سیستم‌های مخابراتی، بهره برحسب بِل (Bel) اندازه‌گیری می‌شود. از گذشته، بل برای اندازه‌گیری نسبت دو توان یا همان بهره توان $$G$$ استفاده می‌شود:

با کمک دسی‌بل (Decibel) می‌توانیم اندازه کوچکتر را نیز بیان کنیم. دسی‌بل $$1/10$$ بل است و به‌صورت زیر تعریف می‌شود:

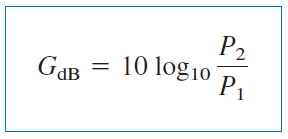
وقتی $$P_1 = P_2$$، تغییری در توان حاصل نشده و بهره برابر با $$0 \, \mathrm {dB}$$ است. اگر $$P_2 = 2 P_1$$، بهره به‌صورت زیر خواهد بود:

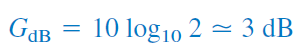
و وقتی $$P_2 = 0.5 P_1$$، بهره برابر است با:

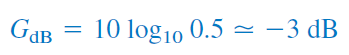
روابط (۶) و (۷) نشان می‌دهند که چرا از لگاریتم استفاده بسیاری می‌شود. لگاریتم معکوس یک کمیت، قرینه لگاریتم آن کمیت است.

بهره $$G$$ را می‌توان براساس نسبت ولتاژ یا جریان نیز بیان کرد. برای این کار، شبکه شکل ۲ را در نظر بگیرید.

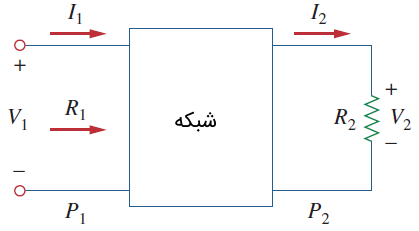
اگر $$P_1$$ توان ورودی و $$P_2$$ توان خروجی (بار)، $$R_1$$ مقاومت ورودی و $$R_2$$ مقاومت بار باشد، آن‌گاه $$P_1 = 0.5 V_1^2 / R_1$$ و $$P_2 = 0.5 V_2^2 / R_2$$ و رابطه (۵) را می‌توان به‌صورت زیر نوشت:

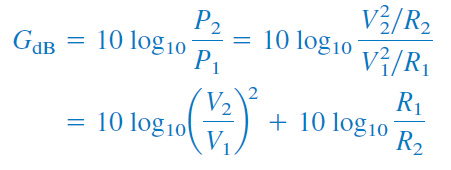
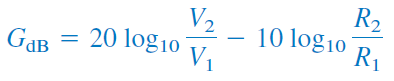
برای حالتی که $$R_2 = R_1$$، رابطه (۹) به‌صورت زیر درمی‌آید:

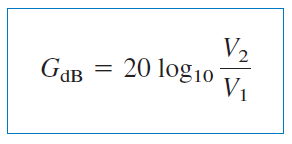
از سوی دیگر، اگر $$P_1 = I_1^2 R_1$$ و $$P_2 = I_2^2 R_2$$ و $$R_1=R_2$$ باشد، داریم:

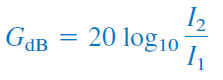
درباره روابط (5)، (10) و (۱۱) سه نکته مهم وجود دارد:

1. عبارت $$10\log _{10}$$ برای توان مورد استفاده قرار می‌گیرید، در حالی که $$20 \log _{10}$$ برای ولتاژ یا جریان به‌کار می‌رود، زیرا توان دوم آن‌ها در رابطه وجود دارد ($$P =V^2/R = I^2R$$).
2. مقدار $$\mathrm {dB}$$ یک مقیاس لگاریتمی از نسبت یک متغیر به متغیری دیگر از همان جنس است. بنابراین، می‌توان آن را بر تعریف تابع شبکه $$H$$ در معادلات (۲-الف) و (۲-ب) که بدون بُعد هستند اعمال کرد. اما برای توصیف $$H$$ در معادلات (۲-ج) و (۲-د) نمی‌توان این کار را انجام داد.
3. در معادلات (10) و (11) فقط از اندازه ولتاژ‌ و جریان استفاده می‌شود. علامت‌های منفی و زاویه‌ها به‌طور مستقل مورد بررسی قرار می‌گیرند.

نمودارهای بُد

محدوده فرکانسی لازم در پاسخ فرکانسی، اغلب گسترده است و استفاده از یک مقیاس خطی برای محور فرکانس، کار دشواری است. همچنین، یک راه نظام‌مندتر برای تعیین ویژگی‌های مهم نموادرهای اندازه و فاز تابع شبکه وجود دارد. به این دلایل، یک روش استاندارد برای رسم تابع شبکه روی دو نمودار نیمه‌لگاریتمی معرفی شده است که در آن، اندازه (برحسب دسی‌بل) براساس لگاریتم فرکانس رسم می‌شود. همچنین، در یک نمودار دیگر، فاز (برحسب درجه) براساس لگاریتم فرکانس رسم می‌شود. این نمودارهای نیمه‌لگاریتمی از تابع شبکه، «نمودارهای بُد» (Bode Plots)‌ نام دارند.

نمودارهای بُد، همان اطلاعات نمودارهای غیرلگاریتمی را به ما می‌دهند و رسم آن‌ها ساده‌تر است.

تابع شبکه را می‌توان به‌صورت زیر نوشت:

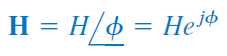
با لگاریتم طبیعی گرفتن از دو طرف رابطه اخیر، داریم:

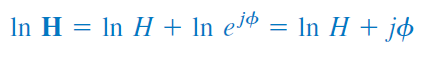
بخش حقیقی $$\mathrm {ln} \, \mathbf {H}$$، تابعی از اندازه است، در حالی که بخش موهومی، فاز را نشان می‌دهد. در یک نمودار اندازه بُد، بهره زیر برحسب دسی‌بل ($$\mathrm {dB}$$) در مقابل فرکانس بیان می‌شود:

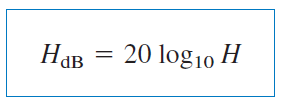
جدول ۱ تعدادی از مقادیر $$H$$ و معادل دسی‌بل آن‌ها را نشان می‌دهد.

در یک نمودار فاز بُد، $$\phi$$ (برحسب درجه) در مقابل فرکانس رسم می‌شود. هردو نمودار اندازه و فاز، در مقیاس نیمه‌لگاریتمی رسم می‌شوند.

تابع شبکه (۳) را می‌توان برحسب عامل‌هایی با بخش‌های حقیقی و موهومی نوشت. در این صورت، نمایش کلی تابع شبکه به‌صورت زیر است:

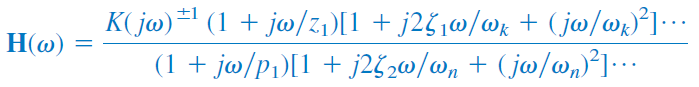
که صفرها و قطب‌های $$\mathbf {H} (\omega )$$ را به‌دست می‌دهد. نمایش $$\mathbf {H} (\omega )$$ در رابطه (15)، فرم استاندارد نامیده می‌شود. تابع $$\mathbf {H} (\omega )$$ ممکن است شامل ۷ نوع عامل مختلف باشد که به فرم‌های مختلف و در ترکیب‌های مختلف در تابع شبکه ظاهر می‌شوند. این عامل‌ها عبارتند از:

1. بهره $$K$$
2. قطب $$(j \omega ) ^ {-1}$$ یا صفر $$( j \omega )$$ در مبدأ
3. قطب ساده $$1/(1+ j \omega /p_1 )$$ یا صفر ساده $$(1+ j \omega /z_1 )$$
4. قطب درجه دوم $$1/[1+2 \zeta _2 \omega / \omega _n + (j \omega / \omega _n )^2]$$ یا صفر درجه دوم $$[1+2 \zeta _1 \omega / \omega _n + (j \omega / \omega _k )^2]$$

برای به‌دست آوردن نمودار بُد، عامل‌ها را به‌صورت جداگانه رسم، سپس آن‌ها را با هم ترکیب می‌کنیم. در ادامه، نحوه رسم هریک از عامل‌هایی را که نام بردیم بیان می‌کنیم. این نمودارها را می‌توان با تقریب بسیار خوبی رسم کرد.

جمله ثابت

اندازه و زاویه بهره $$K$$ به‌ترتیب $$20 \log _{10} K$$ و $$0 ^ \circ$$ است که هردو برای فرکانس‌های مختلف، ثابت هستند. نمودارهای اندازه و فاز بهره در شکل 3 نشان داده شده‌اند. اگر $$K$$ منفی باشد،‌ انداز ه $$20 \log _{10} |K|$$ باقی می‌ماند، اما فاز $$\pm 180^ \circ$$ خواهد شد.

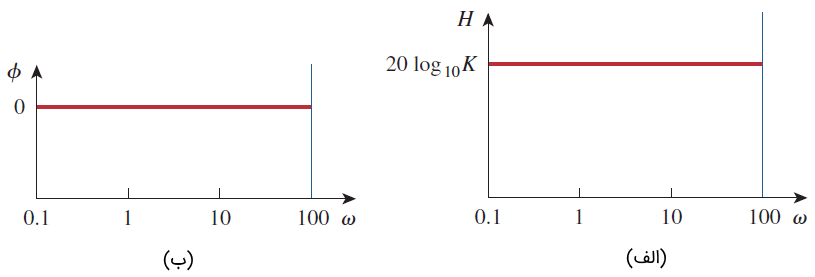
قطب/صفر در مبدأ

برای صفر $$(j \omega)$$ در مبدأ، اندازه $$20 \log _{10} \omega$$ و فاز $$90 ^ \circ$$ است. این نمودارها در شکل ۴ رسم شده‌اند. شیب نمودار اندازه، $$20 \,\, \mathrm {dB/ decade}$$ است، در حالی که مقدار فاز ثابت است.

نمودار بُد قطب $$(j \omega )^ {-1}$$ شبیه نمودار صفر است، با این تفاوت که شیب آن $$-20 \,\, \mathrm {dB/ decade}$$ و فاز $$-90 ^ \circ$$ است. در حالت کلی، برای $$(j \omega ) ^N$$ که $$N$$ یک عدد صحیح است، نمودار اندازه دارای شیب $$20N \,\, \mathrm{dB/decade}$$ است، در حالی که فاز $$90N$$ است.

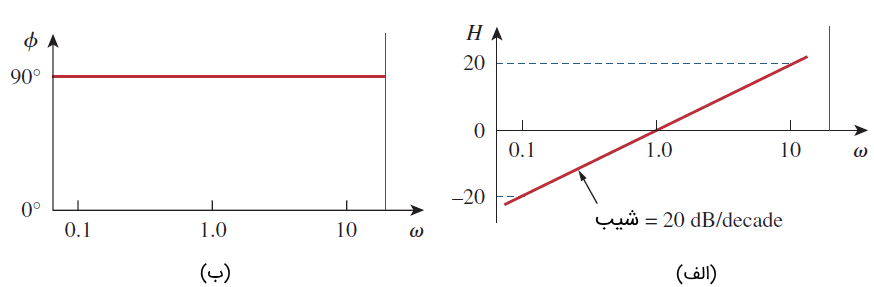
صفر/قطب ساده

برای صفر ساده $$(1+j \omega / z_1)$$، اندازه $$20 \,\, \log _{10} |1+j \omega / z_1 |$$ و فاز $$\tan ^ {-1} \omega / z_1$$ را داریم. در این حالت:

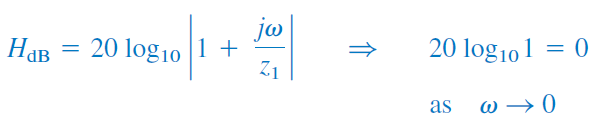
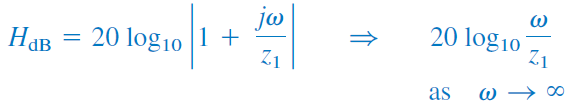
روابط اخیر نشان می‌دهند که می‌توان برای مقادیر کوچک $$\omega$$ اندازه را با صفر (یک خط راست با شیب صفر) و برای مقادیر $$\omega$$ بزرگ با یک خط راست با شیب $$20 \,\, \mathrm {dB/ decade}$$ تقریب زد. فرکانس $$\omega = z _1$$ که در آن، دو خط مجانب به یکدیگر می‌رسند، «فرکانس گوشه» (Corner Frequency) یا «فرکانس شکست» (Break Frequency) نامیده می‌شود. نمودار تقریبی اندازه و نمودار دقیق آن در شکل ۵ (الف) نشان داده شده‌اند.

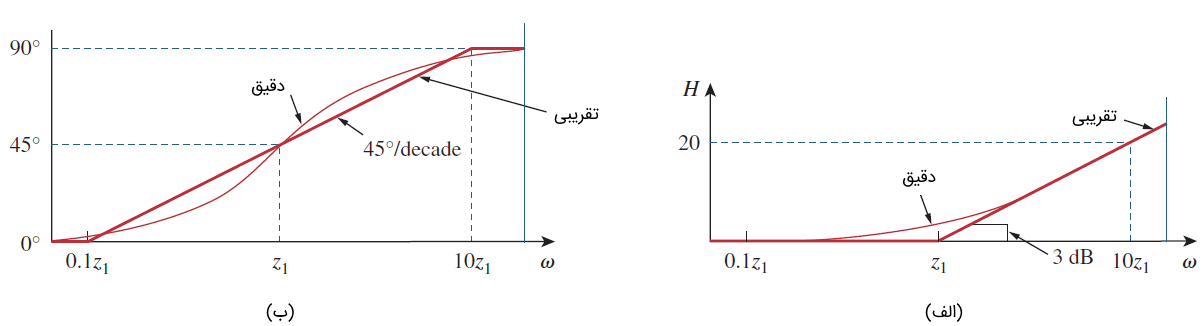
توجه کنید که نمودار تقریبی، به نمودار دقیق نزدیک است؛ جز در فرکانس شکست $$\omega = z_1$$ که مقدار اختلاف برابر است با $$20 \, \log _{10} |(1+j1)|=20\, \log _{10} \sqrt {2} \approx 3 \, \mathrm {dB}$$.

فاز $$\tan ^ {-1} ( \frac{\omega}{z_1})$$ را می‌توان به‌صورت زیر نوشت:

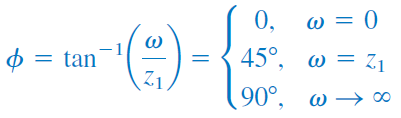
در تقریب خط راست، فاز $$\phi \approx 0$$ را برای $$\omega \le z_1/10$$ و $$\phi \approx 45^ \circ$$ را برای $$\omega = z_1$$ و $$\phi \approx 90^ \circ$$ را برای $$\omega \ge 10 z_1$$ در نظر می‌گیریم.

نمودارهای بُد برای قطب $$1/(1+ j\omega / p_1 )$$ مشابه شکل ۵ هستند، جز فرکانس گوشه $$\omega = p_1$$ که شیب اندازه $$-20 \, \mathrm{dB/decade}$$ و شیب فاز $$-45 ^ \circ$$ بر دهه (decade) است.

قطب/صفر درجه دوم

اندازه قطب درجه دوم $$1/ [1+ j2 \zeta _2 \omega / \omega _n + (j \omega / \omega _n)^2]$$ برابر با $$-20 \log _{10} | 1+ j 2 \zeta _2 \omega / \omega _n + j \omega / \omega _n + (j \omega / \omega _n)^2|$$ و فاز آن،‌ معادلِ $$\tan ^ {-1} ( 2 \zeta _2 \omega / \omega _n )/ (1- \omega ^2 / \omega _n^2)$$ است. برای فرکانس‌های کوچک داریم:

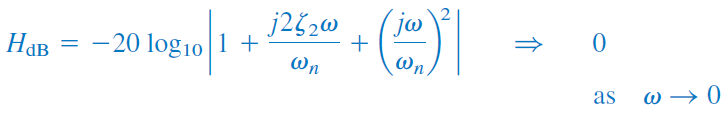
و در فرکانس‌های بزرگ:

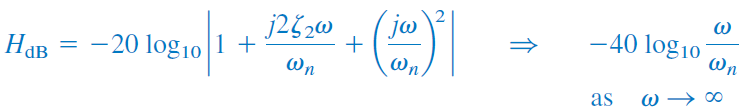
بنابراین، نمودار اندازه دو خط مجانب دارد: یکی با شیب صفر برای $$\omega < \omega _n$$ و دیگری با شیب $$-40 \, \mathrm {dB/decade}$$ برای $$\omega > \omega _n$$ که $$\omega _n$$ فرکانس گوشه است.

شکل ۶ (الف)، نمودارهای اندازه تقریبی و دقیق را نشان می‌دهد. نمودار دقیق، به ضریب میرایی $$\zeta _2$$ و فرکانس گوشه $$\omega _n$$ بستگی دارد. اگر دقت بالایی لازم باشد، پیک قابل‌توجه در مجاورت فرکانس گوشه را باید به تقریب خطی افزود.

فاز را می‌توان به‌صورت زیر بیان کرد:

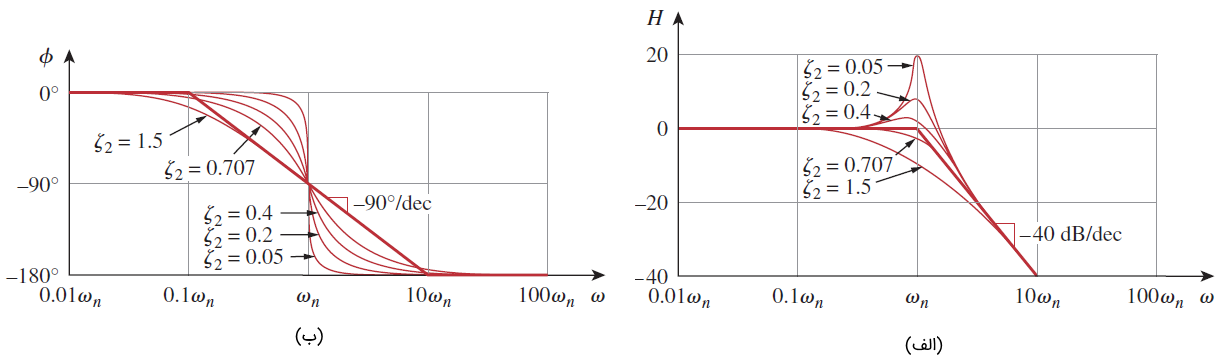
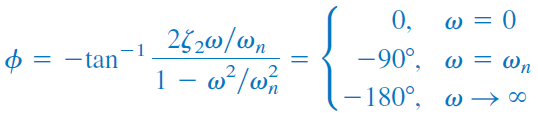
نمودار فاز، خط راستی با شیب $$-90 ^ \circ$$ بر دهه است که از $$\omega _n$$ شروع شده و در $$10 \omega _n$$ تمام می‌شود (شکل ۶ (ب)). مجدداً می‌بینیم که اختلاف نمودار دقیق و خط تقریبی به‌دلیل ضریب میرایی است.

تقریب خطی نمودارهای اندازه و فاز برای قطب‌های مرتبه دوم مشابه قطب‌های تکراری $$(1+j \omega / \omega _n ) ^{-2}$$ است. قطب‌های تکراری، معادل قطب درجه دوم با $$\zeta _2 = 1$$ هستند.

برای صفر درجه دوم، نمودارهای شکل ۶ معکوس می‌شوند، زیرا شیب نمودار اندازه $$40 \, \mathrm {dB/decade}$$ و شیب نمودار فاز $$90 ^ \circ$$ بر دهه است.

جدول ۲، خلاصه نمودارهای بُد را برای هفت عامل نشان می‌دهد. البته در عمل، هر تابع شبکه همه هفت عامل را ندارد. برای رسم نمودارهای بُد تابع شبکه $$\mathbf{H} ( \omega )$$ به‌فرم رابطه (۱۵)، ابتدا فرکانس‌های گوشه را در نمودار نیمه‌لگاریتمی مشخص می‌کنیم،‌ سپس نمودار عامل‌ها را با هم ترکیب می‌کنیم. نمودار ترکیبی، اغلب از چپ به راست و با تغییر مناسب شیب‌ها در هر فرکانس گوشه رسم می‌شود.

مثال

نمودارهای بُد تابع زیر را رسم کنید:

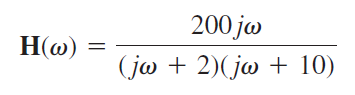
حل: ابتدا $$\mathbf {H} (\omega )$$ را با تقسیم قطب‌ها و صفرها به‌فرم استاندارد می‌نویسیم:

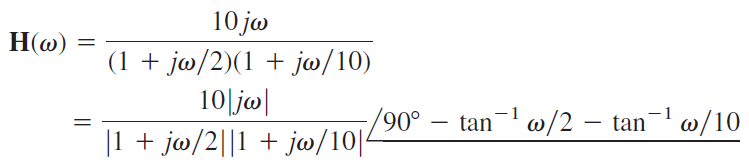
بنابراین، اندازه و فاز به‌صورت زیر هستند:

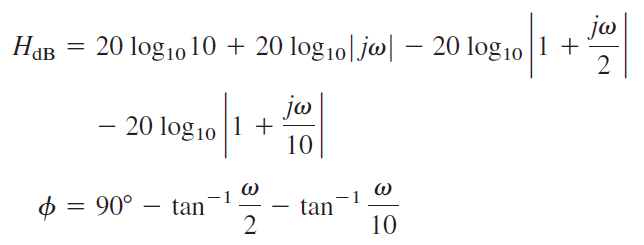
همان‌طور که می‌بینیم، دو فرکانس گوشه در $$\omega =2, 10$$ داریم. نمودار اندازه و فاز هر جمله با خط منقطع رسم، سپس با هم ترکیب شده و خط ممتد به دست آمده است (شکل 7).

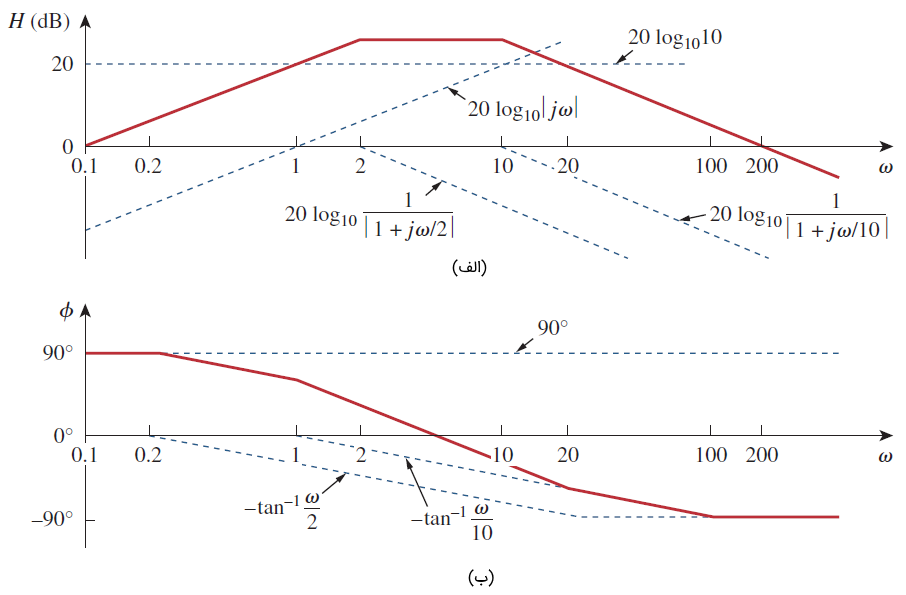
در صورتی که مباحث بیان شده برای شما مفید بوده و می‌خواهید درباره موضوعات مرتبط، مطالب بیشتری یاد بگیرید، پیشنهاد می‌کنیم به آموزش‌های زیر مراجعه کنید:

• دو قطبی در مدارهای الکتریکی — به زبان ساده
• تزویج در مدارهای الکتریکی — مفاهیم اصلی

^^