هارمونیک (Harmonic) در مدارهای AC — از صفر تا صد

رفتار مقاومت در مدارهای AC و مدارهای DC یکسان است. بدین گونه که جریان گذرنده از آن، متناسب با اختلاف ولتاژ دو سرش است. دلیل این امر این است که مقاومت قطعه‌ای خطی است و اگر ولتاژ سینوسی به آن اعمال کنیم، جریان نیز سینوسی خواهد بود و اختلاف فاز آن با ولتاژ صفر است.

وقتی با جریان‌ و ولتاژ متناوب در مدارهای الکتریکی سروکار داریم، فرض می‌کنیم سینوسی خالص هستند و فقط یک فرکانس پایه دارند. البته، این مورد همیشه صادق نیست. اگر مشخصه جریان-ولتاژ در یک دستگاه یا مدار الکتریکی یا الکترونیکی، خطی نباشد، جریان گذرنده از آن متناسب با ولتاژ اعمالی نخواهد بود. شکل موج متناوب این مدارها با شکل موج سینوسی ایده‌آل متفاوت است. این شکل موج‌ها، غیرسینوسی (non-sinusoidal) یا پیچیده (complex) هستند.

شکل‌ موج‌های پیچیده در قطعات الکتریکی مانند سلف‌های هسته آهنی، ترانسفورماتورهای سوئیچینگ، بالاست‌های الکترونیکی در لامپ‌های فلوئورسنت، بارهای بزرگ سلفی و ماشین‌های الکتریکی مانند ژنراتورها وجود دارند. در نتیجه حتی اگر ولتاژ سینوسی باشد، جریان سینوسی نیست.

فیلم آموزش مبانی مهندسی برق ۱ در فرادرس

کلیک کنید

اغلب مدارهای منبع تغذیه سوئیچینگ مانند یکسوکننده‌ها، ترانزیستورهای قدرت، مبدل‌های قدرت و غیره شکل موج سینوسی منابع تغذیه را برای کنترل دور موتور یا تبدیل به شکل موج DC می‌بُرند و پردازش می‌کنند. در این مدارهای سوئیچینگ، تنها مقادیر پیک منبع AC نگه داشته می‌شود و از آن‌جایی که جریان سوئیچینگ غیرسینوسی است، می‌گوییم بار شامل هارمونیک است.

شکل موج‌های پیچیده غیرسینوسی، از ترکیب دنباله‌ای از فرکانس‌های شکل موج سینوسی تشکیل می‌شوند که «هارمونیک» (Harmonics) نام دارند. هارمونیک یک اصطلاح عمومی است که برای توصیف اعوجاج یک شکل موج سینوسی شامل شکل موج‌هایی با فرکانس‌های مختلف استفاده می‌شود. یک شکل موج پیچیده را (با هر شکلی) می‌توان به‌صورت ریاضی به مولفه‌هایی تفکیک کرد که «فرکانس پایه» (fundamental frequency) نامیده می‌شوند.

فرکانس پایه

یک «شکل موج پایه» (Fundamental Waveform)، شکل موجی سینوسی است که فرکانس آن برابر با فرکانس منبع است. فرکانس پایه f، اساسی‌ترین فرکانسی است که یک شکل موج پیچیده بر اساس آن ساخته می‌شود.

فیلم آموزش مدارهای الکتریکی ۱ در فرادرس

کلیک کنید

شکل موج پایه یا هارمونیک اولِ شکل موج AC زیر را در نظر بگیرید.

که در آن، Vmax مقدار پیک ولتاژ برحسب ولت و f فرکانس شکل موج برحسب هرتز است. می‌بینیم که یک شکل موج سینوسی، ولتاژ (یا جریان) متناوبی است که با فرکانس زاویه‌ای $$2\pi f$$ تغییر می‌کند. فرکانس f برابر با تعداد سیکل‌ها در یک ثانیه است.

هارمونیک‌ها، ولتاژها یا جریان‌هایی هستند که در فرکانسی کار می‌کنند که یک ضریب (عدد طبیعی) از فرکانس پایه است. مثلاً برای یک شکل موج پایه 50Hz، می‌توان به فرکانس هارمونیک دوم 100Hz ($$2\times50Hz$$)، فرکانس هارمونیک سوم 150Hz ($$3\times 50Hz$$)، فرکانس هارمونیک پنجم 250Hz ($$5\times 50Hz$$) و... اشاره کرد. به عبارت دیگر، می‌توان گفت فرکانس هارمونیک‌ها ضرایبی از فرکانس پایه است و می‌توان آن‌ها را با ۴f، 3f، ۲f و... نشان داد.

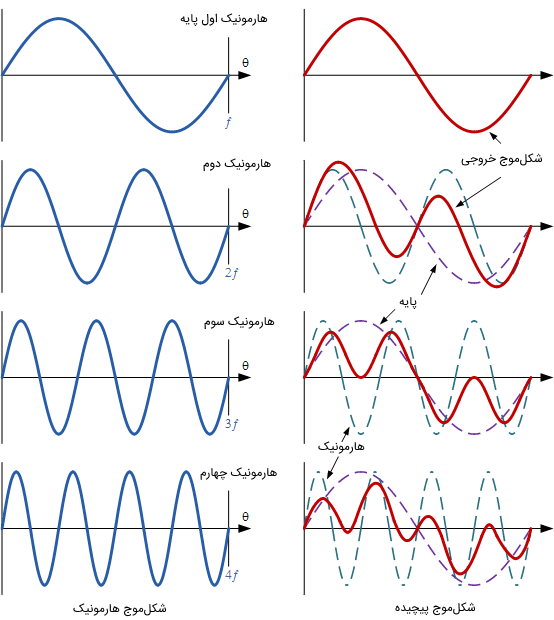
در شکل‌ بالا، موج‌های قرمز، شکل‌‌موج‌های واقعی روی بار هستند که با افزوده شدن هارمونیک به فرکانس پایه ساخته شده‌اند. شکل موج پایه را هارمونیک اول نیز می‌نامند. توجه کنید که شکل موج پیچیده، علاوه بر تعداد و دامنه هارمونیک‌ها، به رابطه فاز بین فرکانس پایه و هارمونیک‌ها بستگی دارد.

دیدیم که شکل موج پیوسته را می‌توان از شکل موج پایه به اضافه هارمونیک‌ها ساخت که هر کدام مقدار پیک و زاویه فاز مربوط به خود را دارند. برای مثال، اگر فرکانس پایه به‌صورت $$E=V_{max}\times (2\pi f t)$$ باشد، مقادیر هارمونیک‌ها به‌شکل زیر خواهد بود.

• برای هارمونیک دوم:

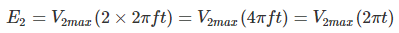
• برای هارمونیک سوم:

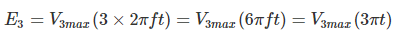
• برای هارمونیک چهارم:

• و... .

در نتیجه، معادله یک شکل موج پیچیده را می‌توان به‌صورت زیر نوشت:

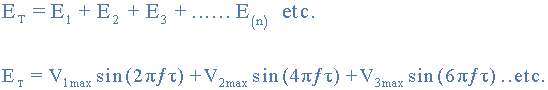
که مجموع هارمونیک‌های تشکیل دهنده آن است.

در آموزش‌های بعدی، درباره سایر موضوعات مرتبط با مدارهای AC بحث خواهیم کرد. اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، پیشنهاد می‌کنیم به آموزش های زیر مراجعه کنید:

• آموزش مدارهای الکتریکی ۱
• آموزش مبانی مهندسی برق ۱
• تقویت کننده های الکترونیکی — مجموعه مقالات جامع وبلاگ فرادرس
• مدارهای جریان مستقیم (DC) — مجموعه مقالات جامع وبلاگ فرادرس

^^