مدولاسیون فاز — راهنمای جامع

مدولاسیون فاز (Phase Modulation) یکی دیگر از تکنیک‌های مدولاسیون محسوب می‌شود که در آن فاز سیگنال حامل (Carrier Signal) متناسب با تغییرات دامنه سیگنال پیام تغییر می‌کند. به عبارت دیگر می‌توان گفت که مدولاسیون فاز، یکی از روش‌های مدولاسیون زاویه (Angle Modulation) است و در آن فاز کلی سیگنال حامل به صورت همگام با دامنه سیگنال پیام تغییر می‌کند. از این تکنیک نیز مانند سایر تکنیک‌های مدولاسیون، برای انتقال سیگنال تا مسافت‌های طولانی استفاده می‌شود و با استفاده از آن، می‌توان سیگنال را نسبت به دریافت نویز بسیار مقاوم‌تر کرد.

عباراتی مانند رادیو AM و رادیو FM برای اکثر ما بسیار آشنا هستند. در حالی که عبارت رادیو PM به نظر می‌رسد در طبقه جداگانه‌ای قرار داشته باشد؛ زیرا این عبارت به هیچ وجه متداول نیست. در حالی که می‌توان گفت مدولاسیون فاز بیشتر به فرکانس‌های رادیویی دیجیتال مرتبط است. بنابراین، رادیو PM نیز به اندازه رادیو FM متداول است؛ زیرا تفاوت بسیار کمی بین مدولاسیون فاز و مدولاسیون فرکانس وجود دارد. در حالت کلی، مدولاسیون فاز و مدولاسیون فرکانس، به عنوان دو تکنیک مختلف از مدولاسیون زاویه مورد استفاده قرار می‌گیرند که کلمه زاویه به تغییر مقدار داده شده (ورودی) به یک تابع سینوسی یا کسینوسی اشاره می‌کند.

دیاگرام مدولاسیون فاز

در مدولاسیون فاز، فاز سیگنال حامل تغییر می‌کند، در حالی که دامنه سیگنال حامل ثابت باقی می‌ماند.

فیلم آموزش مخابرات ۱ – مقدماتی در فرادرس

کلیک کنید

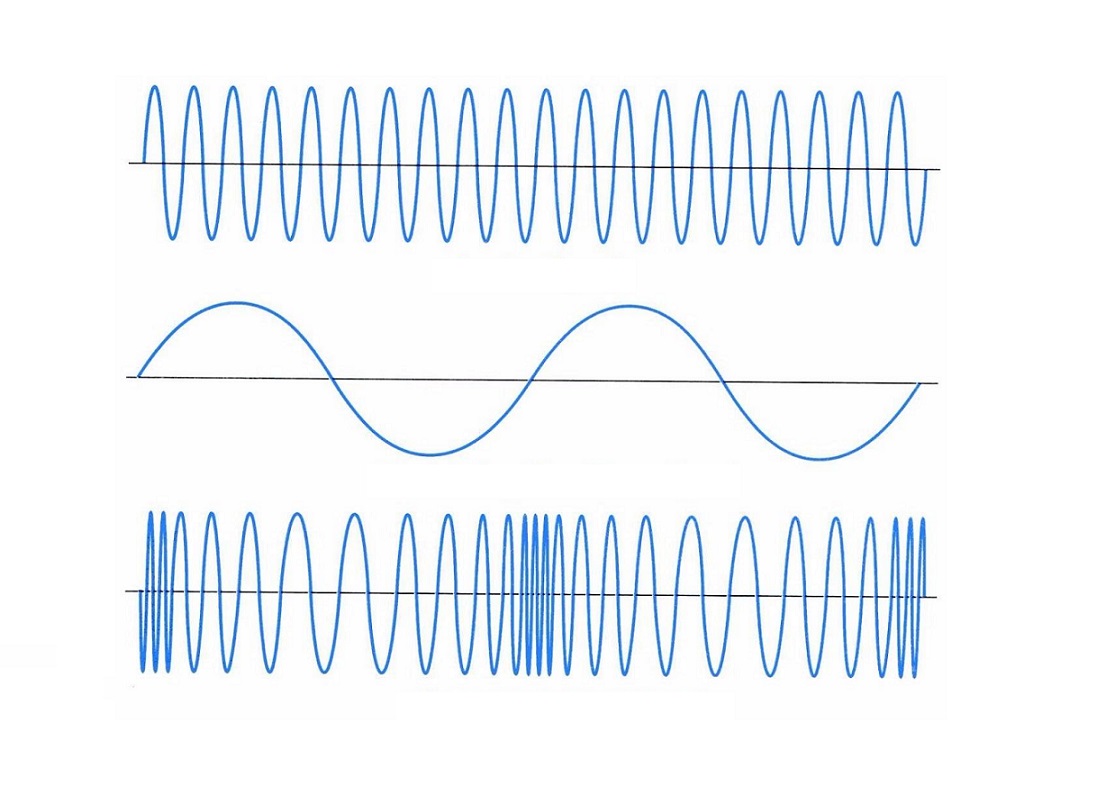
مدولاسیون فاز را به صورت خلاصه مدولاسیون PM نیز می‌گویند. در تصویر زیر نمایی از سه سیگنال پیام، حامل و مدوله شده PM نشان داده شده است.

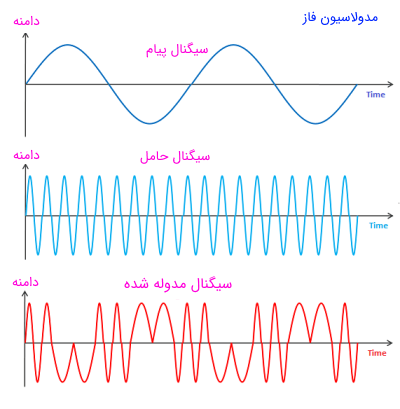
با توجه به شکل سوم، می‌توان به این نکته پی برد که فاز هر دو نیمه تناوب مثبت و منفی در سیگنال حامل، متناسب با تغییرات دامنه سیگنال پیام در حال تغییر هستند. در طول نیمه تناوب مثبت، فاز سیگنال حامل در یک جهت شیفت می‌یابد، در حالی که در نیمه منفی سیگنال، فاز سیگنال حامل در جهت مخالف با آن شیفت می‌یابد. در مدولاسیون فاز، انحراف فاز به صورت مستقیم با دامنه سیگنال پیام متناسب است.

امنیت سیگنال در برابر نویز (Noise Immunity)، در مدولاسیون فاز نسبت به مدولاسیون دامنه بهتر است، در حالی که مدولاسیون فاز در این ویژگی نسبت به مدولاسیون فرکانس (Frequency Modulation) عملکرد ضعیف‌تری دارد. همچنین نسبت سیگنال به نویز (Signal-to-Noise) یا SNR، در مدولاسیون فاز به خوبی SNR در مدولاسیون فرکانس نیست. شاخص مدولاسیون در مدولاسیون فرکانس به صورت مستقیم با سیگنال پیام متناسب است. از مدولاسیون فاز برای سرویس‌های رادیویی متحرک استفاده می‌شود.

البته مدولاسیون فاز و مدولاسیون فرکانس تا حد زیادی به یکدیگر مرتبط هستند. هم در مدولاسیون فاز و هم در مدولاسیون فرکانس، زاویه فاز سیگنال مدوله شده تغییر می‌کند. در عمل نیز مدولاسیون فاز و مدولاسیون فرکانس به یکدیگر متکی هستند. زمانی که فاز سیگنال حامل تغییر کند، فرکانس سیگنال حامل نیز تغییر می‌کند. به طریق مشابه، با تغییر کردن فرکانس سیگنال حامل، فاز آن نیز تغییر می‌کند. با این حال، مدولاسیون فاز و مدولاسیون فرکانس به صورت مستقیم با یکدیگر متناسب نیستند.

در مدولاسیون فرکانس، زاویه فاز کلی سیگنال حامل، برای بازه کوتاهی از زمان به دلیل تغییر در فرکانس سیگنال حامل تغییر می‌کند. اما در مدولاسیون فاز، فرکانس سیگنال حامل برای بازه کوتاهی از زمان به دلیلی تغییر در فاز سیگنال حامل تغییر می‌کند.

بیان ریاضی مدولاسیون فاز

در مطلب مدولاسیون فرکانس در مجله فرادرس، دیدیم که با افزودن انتگرال سیگنال باند پایه به آرگومان (Argument) یک تابع سینوسی یا کسینوسی، می‌توان یک سیگنال مدوله شده فرکانس را به دست آورد. در این حالت تابع سینوسی یا کسینوسی، همان سیگنال حامل محسوب می‌شوند. در نتیجه عبارت زیر برای یک سیگنال مدوله شده فرکانس به دست می‌آید:

$$x_{FM}(t)=\sin(\omega_Ct+\int_{-\infty}^{t} x_{BB}(t)dt)$$

فیلم آموزش ریاضی مهندسی – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

اگر در مدولاسیون فرکانس، به جای افزودن انتگرال سیگنال باند پایه، خود سیگنال باند پایه را به آرگومان تابع سینوسی یا کسینوسی اضافه کنیم، آن‌گاه این تکنیک را مدولاسیون فاز یا PM می‌گویند و چنین عملی باعث می‌شود که فاز سیگنال مدوله شده متناسب با دامنه سیگنال پیام یا باند پایه تغییر کند. بنابراین، می‌توان گفت که مدولاسیون فاز در واقع اندکی نسبت به مدولاسیون فرکانس ساده‌تر است. سیگنال مدوله شده توسط مدولاسیون فاز را می‌توان به صورت زیر به دست آورد:

$$x_{PM}(t)=\sin(\omega_Ct+x_{BB}(t))$$

در فرمول بالا، $$x_{BB}(t)$$ سیگنال باند پایه و $$\omega_C$$ برابر با فاز سیگنال حامل است. $$x_{PM}(t)$$ برابر با سیگنال مدوله شده تحت مدولاسیون فاز است.

درست همانند مدولاسیون فرکانس، در مدولاسیون فاز نیز می‌توانیم شاخص مدولاسیون (Modulation Index) را تعریف کنیم. از شاخص مدولاسیون می‌توان استفاده کرد و انحراف‌ فاز را نسبت به تغییرات مقادیر سیگنال باند پایه حساس‌تر (Sensitive) کرد. در فرمول زیر از شاخص مدولاسیون در محاسبه سیگنال مدوله شده استفاده شده است:

$$x_{PM}(t)=\sin(\omega_Ct+mx_{BB}(t))$$

شباهت بین مدولاسیون فرکانس و مدولاسیون فاز زمانی واضح‌تر می‌شود که یک سیگنال باند پایه با یک فرکانس (تک فرکانس) را در نظر بگیریم. فرض کنیم که $$x_{BB}(t) = \sin ( \omega_{BB}t )$$ باشد، آن‌گاه انتگرال سیگنال سینوسی، برابر با منفی سیگنال کسینوسی می‌شود. البته یک مقدار ثابت نیز وجود دارد که در اینجا می‌توان از آن صرف نظر کرد. به عبارت دیگر، حاصل انتگرال برابر با یک سیگنال شیفت یافته زمانی سیگنال اصلی می‌شود.

بنابراین، اگر روی این سیگنال باند پایه، همزمان هم مدولاسیون فاز و هم مدولاسیون فرکانس اعمال کنیم، تنها تفاوتی که ایجاد می‌شود در این است که سیگنال مدوله شده بین مقدار باند پایه و تغییرات در سیگنال حامل، تنظیم (Alignment) می‌شود و خود تغییرات یکسان هستند. این مفهوم در بخش بعدی که به نمودارهای حوزه زمان می‌پردازیم به صورت واضح‌تر مشخص خواهد شد.

به یاد داشتن این نکته مهم است که در مدولاسیون فاز با فاز لحظه‌ای سر و کار داریم، درست همان گونه که در مدولاسیون فرکانس با فرکانس لحظه‌ای رو‌به‌رو هستیم. واژه فاز در مدولاسیون فاز شاید اندکی مبهم باشد. معنی آشناتر این واژه به حالت اولیه (Initial State) یک سیگنال سینوسی اشاره می‌کند. به عنوان مثال، یک سیگنال سینوسی نرمال، با مقدار صفر شروع می شود و سپس به سمت مقدار بیشینه خود افزایش می‌یابد. یک سیگنال سینوسی که در یک نقطه متفاوت از دوره تناوب خود شروع شود، دارای افست فاز (Phase Offset) خواهد بود. البته می‌توان فاز را به عنوان یک سهم مشخص از تناوب شکل موج کامل نیز در نظر گرفت. به عنوان مثال، در فاز $$\frac {\pi} {2}$$، یک سیگنال سینوسی یک چهارم از دوره تناوب کلی خود را کامل کرده است.

اما این تفاسیر فاز، کمک زیادی به ما نمی‌کنند؛ زیرا در تکنیک مدولاسیون فاز، با فازی رو به رو هستیم که به صورت پیوسته در پاسخ به تغییرات سیگنال باند پایه تغییر می‌کند. به عبارت دیگر، فاز در یک لحظه مفروض، متناظر با مقدار تابع مثلثاتی در آن لحظه است. می‌توان تغییرات پیوسته در فاز لحظه‌ای را به عنوان حرکت سیگنال حامل برای دور شدن و یا نزدیک شدن به حالت قبلی شکل موج دانست.

نکته مهم دیگر که باید به یاد داشته باشیم این است که توابع مثلثاتی مانند سینوس و یا کسینوس، روی زاویه عمل می‌کنند. تغییر آرگومان یک تابع مثلثاتی متناظر با تغییر در زاویه است و این خود دلیلی است بر این موضوع که چرا مدولاسیون فاز و مدولاسیون فرکانس هر دو جزو مدولاسیون زاویه محسوب می‌شوند.

مدولاسیون فاز در حوزه زمان

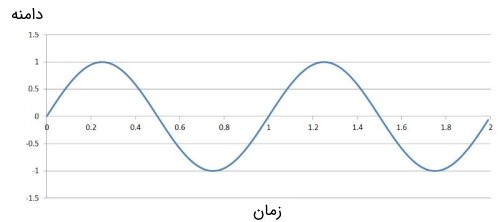
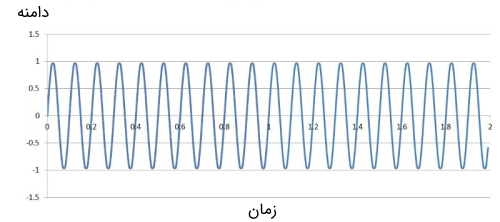
فرض کنید یک سیگنال حامل با فرکانس 10 مگا هرتز و یک سیگنال باند پایه سینوسی با فرکانس ۱ مگا هرتز وجود داشته باشند. در تصویر زیر نمایی از این دو سیگنال را می‌توان دید.

در تصویر زیر، سیگنال مدوله شده فرکانس (با m=4) نشان داده شده است.

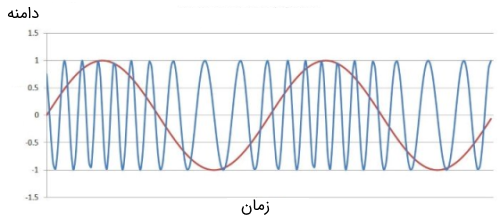
می‌توانیم سیگنال مدوله شده فاز را بر اساس معادله زیر به دست بیاوریم.

$$x_{PM}(t)=\sin((10\times10^6\times2\pi t)+\sin(1\times10^6\times2\pi t))$$

در این معادله، سیگنال پیام را به آرگومان سیگنال حامل اضافه می‌کنیم. در مدولاسیون فاز سیگنال اصلی مثبت است و با همین علامت عمل جمع را انجام می‌دهیم. در واقع در مدولاسیون فاز برخلاف مدولاسیون فرکانس از منفی کسینوس، که انتگرال سیگنال اصلی است، استفاده نمی‌کنیم. در تصویر زیر نمایی از سیگنال مدوله شده فاز را می‌توان مشاهده کرد.

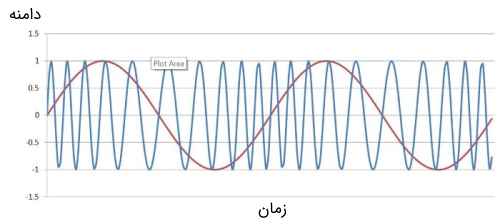
قبل از ادامه بحث، ایده بسیار خوبی است که نمودار سیگنال مدوله شده فاز و نمودار سیگنال مدوله شده فرکانس را در کنار یکدیگر ترسیم کنیم. تصویر زیر نمایی از این دو سیگنال را نشان می‌دهد.

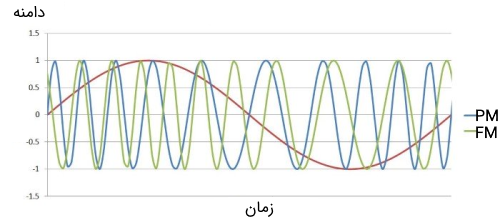
در این تصویر، اولین نکته‌ای که باید به آن توجه کرد، این است که از دیدگاه ظاهری عملکرد سیگنال مدوله شده فرکانس نسبت به سیگنال مدوله شده فاز قابل درک‌تر است. ارتباط واضحی بین قسمت فرکانس بالا و قسمت فرکانس پایین در سیگنال مدوله شده و مقادیر بزرگ و کوچک در سیگنال باند پایه وجود دارد. در حالی که در مدولاسیون فاز، رابطه بین سیگنال باند پایه و رفتار سیگنال حامل به صورت واضح و مستقیم دیده نمی‌شود.

البته بعد از اندکی تامل و دقت در نمودار، می‌توان دید فرکانس سیگنال مدوله شده در مدولاسیون فاز، متناظر با شیب سیگنال باند پایه است. قسمت فرکانس بالای سیگنال مدوله شده فاز، در طول قسمت‌های با شیب تند مثبت سیگنال پیام ($$X_{BB}$$) اتفاق می‌افتد و قسمت‌های فرکانس پایین سیگنال، در طول قسمت‌های با شیب تند منفی به وجود می‌آیند.

این تفسیر کاملا معنادار است؛ زیرا می‌دانیم که فرکانس به صورت تابعی از زمان و حاصل مشتق فاز است که خود فاز نیز تابعی از زمان محسوب می‌شود. در مدولاسیون فاز، شیب سیگنال باند پایه تعیین می‌کند که فاز با چه سرعتی تغییر خواهد کرد و سرعتی که در آن فاز تغییر می‌کند، معادل با فرکانس است. بنابراین در یک سیگنال مدوله شده فاز، شیب بزرگ در سیگنال باند پایه، متناظر با فرکانس بالا در سیگنال PM و شیب کم در سیگنال باند پایه، متناظر با فرکانس پایین در سیگنال مدوله شده فاز است.

همان طور که گفتیم در مدولاسیون فرکانس، از انتگرال سیگنال باند پایه استفاده می‌کنیم و تاثیری که در سیگنال دارد این است که قسمت فرکانس بالا سیگنال حامل را به قسمت مقادیر بزرگ سیگنال پیام منتقل می‌کند که پس از قسمت با شیب تند بزرگ قرار گرفته‌اند.

مدولاسیون فاز در حوزه فرکانس

بر اساس نمودارهای حوزه زمان که در قسمت قبلی به توضیح آن‌ها پرداختیم، مدولاسیون فاز و مدولاسیون فرکانس بسیار شبیه به یکدیگر هستند. به همین دلیل جای تعجب ندارد که نمودارهای این دو نوع مدولاسیون در حوزه فرکانس نیز بسیار شبیه به یکدیگر باشند. در تصویر زیر نمودارهای طیف (Spectra) مدولاسیون فاز با سیگنال‌های حامل و پیام ذکر شده در بالا ترسیم شده‌اند.

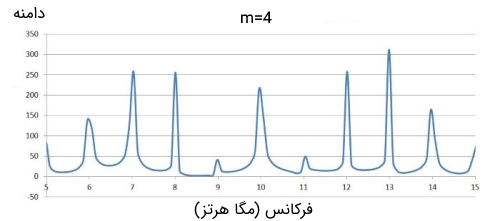
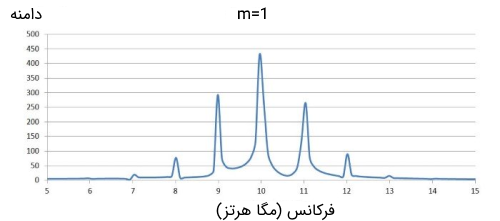
خلاصه مدولاسیون فاز

• مدولاسیون فاز از طریق اضافه کردن سیگنال باند پایه به آرگومان تابع سینوسی یا کسینوسی به دست می‌آید. در واقع توابع سینوسی و کسینوسی نشان دهنده سیگنال حامل هستند.
• شاخص مدولاسیون نشان‌دهنده حساسیت تغییرات فاز سیگنال مدولاسیون فاز نسبت به رفتار سیگنال باند پایه است.
• تاثیرات مدولاسیون فاز در حوزه فرکانس مشابه با تاثیرات مدولاسیون فرکانس در این حوزه است.
• می‌توان گفت مدولاسیون فاز آنالوگ نسبتا متداول نیست، اما مدولاسیون فاز دیجیتال با گستردگی بسیار زیادی مورد استفاده قرار می‌گیرد.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• آموزش مبانی ​الکترونیک – مفاهیم تئوریک به همراه شبیه سازی عملی و کاربردی
• مدولاسیون دامنه — از صفر تا صد
• دمدولاسیون دامنه — از صفر تا صد
• انرژی و توان سیگنال -- از صفر تا صد

^^