در آموزشهای قبلی مجله فرادرس ، درباره پارامترهای خط انتقال و پخش بار در سیستم قدرت بحث کردیم. در این آموزش با مدل خط انتقال آشنا میشویم. قبل از مطالعه این آموزش، میتوانید مطلب «دوقطبی در مدارهای الکتریکی » را نیز بررسی کنید.
پارامترهای ABCD مدل خط انتقال
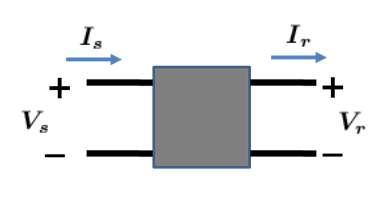
یک خط انتقال هوایی را به صورت یک دوقطبی در نظر میگیریم:
شکل ۱: نمایش دوقطبی که در آن، V s \boldsymbol { V _ { s } } V s V r \boldsymbol { V _ { r } } V r I s \boldsymbol { I _ { s } } I s I r \boldsymbol { I _ { r } } I r
فرض کنید بتوان سیستم را با معادلات کمیتهای ابتدای خط بر حسب کمیتهای انتهای خط به صورت زیر توصیف کرد:
V s = A V r + B I r I s = C V r + D I r \large \begin {align*} \boldsymbol { V _ { s } } & = A \boldsymbol { V _{ r } } + B \boldsymbol { I _ { r } } \\
\boldsymbol { I _ { s } } & = C \boldsymbol { V _ { r } } + D \boldsymbol { I _ { r } }
\end {align*} V s I s = A V r + B I r = C V r + D I r
که در آن، A A A B B B C C C D D D
پارامترهای ABCD را میتوان به فرم ماتریسی زیر نوشت:
[ V s I s ] = [ A C B D ] [ V r I r ] \large \left [ \begin {matrix} \boldsymbol { V _ { s } } \\ \boldsymbol { I _ { s } } \end {matrix} \right ] = \left [ \begin {matrix}
A & C \\
B & D \end {matrix} \right ]
\left [ \begin {matrix} \boldsymbol { V _ { r } } \\ \boldsymbol { I _ { r } } \end {matrix} \right] [ V s I s ] = [ A B C D ] [ V r I r ]
مدل بدون تلفات خط
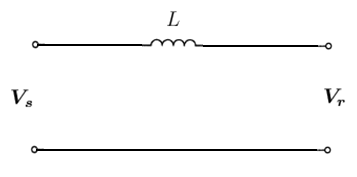
سادهترین مدل خط انتقال که در آن از مقاومت و خازن صرفنظر میشود، مدل بدون تلفات نام دارد.
شکل ۲: مدل بدون تلفات خط این مدل، به عنوان یک سلف خالص، یعنی با امپدانس زیر نشان داده میشود:
Z = j ω L = X L \large \boldsymbol { Z } = j \omega L = X _ { L } Z = jω L = X L
با استفاده از قوانین کیرشهف ، میتوانیم روابط زیر را بنویسیم:
V s = V r + X L I r I s = I r \large \begin {align*} \boldsymbol { V _ { s } } & = \boldsymbol { V _ { r } } + X _ { L } \boldsymbol { I _ { r } } \\
\boldsymbol { I _ { s } } & = \boldsymbol { I _ { r } } \end {align*} V s I s = V r + X L I r = I r
بنابراین، پارامترهای ABCD خط بدون تلفات (L) به صورت زیر خواهد بود:
[ V s I s ] = [ 1 X L 0 1 ] [ V r I r ] \large \left [ \begin {matrix} \boldsymbol { V _ { s } } \\ \boldsymbol { I _ { s } } \end {matrix} \right ] = \left [ \begin {matrix}
1 & X _ { L } \\
0 & 1 \end {matrix} \right ]
\left [ \begin {matrix} \boldsymbol { V _ { r } } \\ \boldsymbol { I _ { r } } \end {matrix} \right ] [ V s I s ] = [ 1 0 X L 1 ] [ V r I r ]
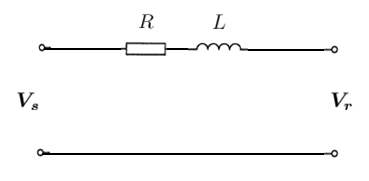
مدل RL خط
با افزودن یک مقاومت سری با سلف، مدل خط انتقال را واقعیتر کرد.
شکل ۳: مدل خط RL در این حالت، امپدانس خط به صورت زیر خواهد بود:
Z = R + j ω L \large \boldsymbol { Z } = R + j \omega L Z = R + jω L
مانند حالت قبل، مقادیر ابتدای خط را بر حسب مقادیر انتهای خط مینویسیم:
V s = V r + Z I r I s = I r \large \begin {align*} \boldsymbol { V _ { s } } & = \boldsymbol { V _ { r } } + \boldsymbol { Z } \boldsymbol { I _ { r } } \\
\boldsymbol { I _ { s } } & = \boldsymbol { I _ { r } } \end {align*} V s I s = V r + Z I r = I r
بنابراین، پارامترهای ABCD خط به صورت زیر خواهند بود:
[ V s I s ] = [ 1 Z 0 1 ] [ V r I r ] \large \left [ \begin {matrix} \boldsymbol { V _ { s } } \\ \boldsymbol { I _ { s } } \end {matrix} \right ] = \left [ \begin {matrix}
1 & \boldsymbol { Z } \\
0 & 1 \end {matrix} \right ]
\left [ \begin {matrix} \boldsymbol { V_ { r } } \\ \boldsymbol { I _ { r } } \end {matrix} \right ] [ V s I s ] = [ 1 0 Z 1 ] [ V r I r ]
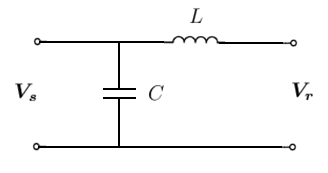
مدل بدون تلفات LC خط
در دو مدل قبلی، خازن را در نظر نگرفتیم. اما در ولتاژهای بالاتر و خطوط طولانیتر، اثر خازن شنت قابل توجه است. بنابراین، در این مدل، خط LC را در نظر میگیریم. شکل زیر، مدل مداری این خط را نشان میدهد.
شکل ۴: مدل خط انتقال بدون تلفات LC اندوکتانس و ظرفیت را میتوان با راکتانس و سوسپتانس زیر نشان داد:
X L = j ω L Y C = j ω C \large \begin {align*} X _ { L } & = j \omega L \\
Y _ { C } & = j \omega C \end {align*} X L Y C = jω L = jω C
با استفاده از قوانین مداری کیرشهف، روابط زیر را داریم:
V s = V r + X L I r I s = Y C V s + I r = Y C V r + ( 1 + X L Y C ) I r \large \begin {align*}
\boldsymbol { V _ { s } } & = \boldsymbol { V _ { r } } + X _ { L } \boldsymbol { I _ { r } } \\
\boldsymbol { I _ { s } } & = Y _ { C } \boldsymbol { V _ { s } } + \boldsymbol { I _ { r } } \\
& = Y _ { C} \boldsymbol { V _ { r } } + \left ( 1 + X _ { L } Y _ { C } \right ) \boldsymbol { I _ { r } }
\end {align*} V s I s = V r + X L I r = Y C V s + I r = Y C V r + ( 1 + X L Y C ) I r
بنابراین، پارامترهای ABCD خط انتقال LC به فرم ماتریسی زیر خواهند بود:
[ V s I s ] = [ 1 X L Y C 1 + X L Y C ] [ V r I r ] \large \left [ \begin {matrix} \boldsymbol { V _ { s } } \\ \boldsymbol { I _ { s } } \end {matrix} \right ] = \left [ \begin {matrix}
1 & X _ { L } \\
Y _ { C } & 1 + X _ { L } Y _ { C } \end {matrix} \right ]
\left [ \begin {matrix} \boldsymbol { V _ { r } } \\ \boldsymbol { I _ { r } } \end {matrix} \right ] [ V s I s ] = [ 1 Y C X L 1 + X L Y C ] [ V r I r ]
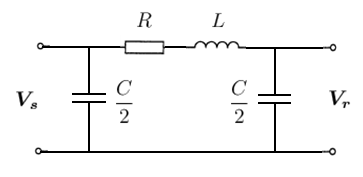
مدل π \Large \pi π
مدل موسوم به π \pi π
π \pi π شکل ۵: مدل π \pi π اجزای سری را میتوان با یک امپدانس و هر یک از خازنهای موازی را با سوسپتانس نشان داد:
Z = R + j ω L Y 2 = j ω ( C 2 ) \large \begin {align*} \boldsymbol { Z } = R + j \omega L \\
\frac { \boldsymbol { Y } } { 2 } = j \omega \left ( \frac { C } { 2 } \right) \end {align*} Z = R + jω L 2 Y = jω ( 2 C )
قبل از تحلیل مدار، جریان گذرنده از امپدانس سری Z \mathbf{Z} Z
I z = I r + Y 2 V r \large \boldsymbol { I _ { z } } = \boldsymbol { I _ { r } } + \frac { \boldsymbol { Y } } { 2 } \boldsymbol { V _ { r } } I z = I r + 2 Y V r
با استفاده از KVL، داریم:
V s = V r + Z I z \large \boldsymbol { V _ { s} } = \boldsymbol { V _ { r } } + \boldsymbol { Z } \boldsymbol { I _ { z } } V s = V r + Z I z
با جایگذاری I z \boldsymbol{I_{z}} I z
V s = V r + Z ( I r + Y 2 V r ) = ( 1 + Z Y 2 ) V r + Z I r I s = Y 2 V s + Y 2 V r + I r = Y 2 [ ( 1 + Z Y 2 ) V r + Z I r ] + Y 2 V r + I r = Y ( 1 + Z Y 4 ) V r + ( 1 + Z Y 2 ) I r \large \begin {align*} \boldsymbol { V _ { s } } & = \boldsymbol { V _ { r } } + \boldsymbol { Z } \left ( \boldsymbol { I _ { r } } + \frac { \boldsymbol { Y } } { 2 } \boldsymbol { V _ { r } } \right) \\
& = \left ( 1 + \frac { \boldsymbol { Z } \boldsymbol { Y } } { 2 } \right ) \boldsymbol { V _ { r } } + \boldsymbol { Z } \boldsymbol { I _ { r } } \\
\boldsymbol { I _ { s } } & = \frac { \boldsymbol { Y } } { 2 } \boldsymbol { V _ { s } } + \frac { \boldsymbol { Y } } { 2 } \boldsymbol { V _ { r } } + \boldsymbol { I _ { r } } \\
& = \frac { \boldsymbol { Y } } { 2 } \left [ \left ( 1 + \frac { \boldsymbol { Z } \boldsymbol { Y } } { 2 } \right ) \boldsymbol { V _ { r } } + \boldsymbol { Z } \boldsymbol { I _ { r } } \right ] + \frac { \boldsymbol { Y } } { 2 } \boldsymbol { V _ { r } } + \boldsymbol { I _ { r } } \\
& = \boldsymbol { Y } \left ( 1 + \frac { \boldsymbol { Z } \boldsymbol { Y } } { 4 } \right ) \boldsymbol { V _ { r } } + \left ( 1 + \frac { \boldsymbol { Z } \boldsymbol { Y } } { 2 } \right ) \boldsymbol { I _ { r } } \end {align*} V s I s = V r + Z ( I r + 2 Y V r ) = ( 1 + 2 Z Y ) V r + Z I r = 2 Y V s + 2 Y V r + I r = 2 Y [ ( 1 + 2 Z Y ) V r + Z I r ] + 2 Y V r + I r = Y ( 1 + 4 Z Y ) V r + ( 1 + 2 Z Y ) I r
بنابراین، پارامترهای ABCD مدل π \pi π
[ V s I s ] = [ ( 1 + Z Y 2 ) Z Y ( 1 + Z Y 4 ) ( 1 + Z Y 2 ) ] [ V r I r ] \large \left [ \begin {matrix} \boldsymbol { V _ { s } } \\ \\ \boldsymbol { I _ { s } } \end {matrix} \right ] = \left [ \begin {matrix}
\left ( 1 + \frac { \boldsymbol { Z } \boldsymbol { Y } } { 2 } \right ) & \boldsymbol { Z } \\ \\
\boldsymbol { Y } \left ( 1 + \frac { \boldsymbol { Z } \boldsymbol { Y } } { 4 } \right ) & \left ( 1 + \frac { \boldsymbol { Z } \boldsymbol { Y } } { 2 } \right ) \end {matrix} \right ]
\left [ \begin {matrix} \boldsymbol { V _ { r } } \\ \\ \boldsymbol { I _ { r } } \end {matrix} \right ] V s I s = ( 1 + 2 Z Y ) Y ( 1 + 4 Z Y ) Z ( 1 + 2 Z Y ) V r I r
مدار خط با پارامتر توزیع شده
مدلهایی که در بالا ارائه شد، متمرکز و فشرده شدهاند، به طوری که خط با پارامترهای R R R L L L C C C R R R L L L C C C
یک مدل با پارامتر توزیع شده را در نظر میگیریم که در آن، ولتاژ و جریان هر نقطه x x x
V ( x ) = cosh ( γ x ) V r + Z c sinh ( γ x ) I r \large \mathbf { V } ( x ) = \cosh ( \mathbf { \gamma } x ) \mathbf { V _ { r } } + \mathbf { Z } _ { c } \sinh ( \mathbf { \gamma } x ) \mathbf { I _ { r } } V ( x ) = cosh ( γ x ) V r + Z c sinh ( γ x ) I r
I ( x ) = 1 Z c sinh ( γ x ) V r + cosh ( γ x ) I r \large \mathbf { I } ( x ) = \frac { 1 } { \mathbf { Z } _ { c } } \sinh ( \mathbf { \gamma } x ) \mathbf { V _ { r } } + \cosh ( \mathbf { \gamma } x ) \mathbf { I _ { r } } I ( x ) = Z c 1 sinh ( γ x ) V r + cosh ( γ x ) I r
که در آن، γ = z y \boldsymbol { \gamma } = \sqrt { \boldsymbol { z y } } γ = zy m − 1 m^{-1} m − 1 Z c = z y \boldsymbol{Z}_{c} = \sqrt{{\boldsymbol{{\frac{z}{y}}}}} Z c = y z
با بررسی معادلات، پارامترهای ABCD را میتوان به فرم ماتریسی (برای خطی به طول l l l
[ V s I s ] = [ cosh ( γ l ) Z c sinh ( γ l ) 1 Z c s i n h ( γ l ) cosh ( γ l ) ] [ V r I r ] \large \left[ \begin {matrix} \boldsymbol { V _ { s } } \\ \\ \boldsymbol { I _ { s } } \end {matrix} \right] = \left[ \begin {matrix}
\cosh ( \boldsymbol { \gamma } l ) & \boldsymbol { Z } _ { c } \sinh ( \boldsymbol { \gamma } l ) \\ \\
\frac { 1 } { \boldsymbol { Z } _ { c } } sinh ( \boldsymbol { \gamma} l ) & \cosh ( \boldsymbol { \gamma } l ) \end {matrix} \right]
\left[ \begin {matrix} \boldsymbol { V _ { r } } \\ \\ \boldsymbol { I _ { r } } \end {matrix} \right] \, V s I s = cosh ( γ l ) Z c 1 s inh ( γ l ) Z c sinh ( γ l ) cosh ( γ l ) V r I r
مدل π \Large {\pi} π
مدل خط π \pi π π \pi π Z \boldsymbol{Z} Z Y C Y_{C} \, Y C
[ A C B D ] = [ ( 1 + Z ′ Y ′ 2 ) Z ′ Y ′ ( 1 + Z ′ Y ′ 4 ) ( 1 + Z ′ Y ′ 2 ) ] = [ cosh ( γ l ) Z c sinh ( γ l ) 1 Z c s i n h ( γ l ) cosh ( γ l ) ] \large \left [ \begin {matrix} A & C \\
B & D \end {matrix} \right ] = \left [ \begin {matrix} \left ( 1 + \frac { \boldsymbol { Z ^ \prime } \boldsymbol { Y ^ \prime } } { 2 } \right ) & \boldsymbol { Z ^ \prime } \\ \\
\boldsymbol { Y ^ \prime } \left ( 1 + \frac { \boldsymbol { Z ^ \prime } \boldsymbol { Y ^ \prime } } { 4 } \right ) & \left ( 1 + \frac { \boldsymbol { Z ^ \prime } \boldsymbol { Y ^ \prime } } { 2 } \right ) \end {matrix} \right ] = \left [ \begin {matrix} \cosh ( \boldsymbol { \gamma } l ) & \boldsymbol { Z } _ { c } \sinh ( \boldsymbol { \gamma } l ) \\ \\
\frac { 1 } { \boldsymbol { Z } _ { c } } sinh ( \boldsymbol { \gamma } l ) & \cosh ( \boldsymbol { \gamma } l ) \end {matrix} \right ] [ A B C D ] = ( 1 + 2 Z ′ Y ′ ) Y ′ ( 1 + 4 Z ′ Y ′ ) Z ′ ( 1 + 2 Z ′ Y ′ ) = cosh ( γ l ) Z c 1 s inh ( γ l ) Z c sinh ( γ l ) cosh ( γ l )
که در آن، Z ′ \boldsymbol{Z'} Z ′ Y ′ \boldsymbol{Y'} \, Y ′ γ = z y \boldsymbol{\gamma} = \sqrt{\boldsymbol{zy}} γ = zy m − 1 m^{-1} m − 1 Z c = z y \boldsymbol{Z}_{c} = \sqrt{\boldsymbol{\frac{z}{y}}} Z c = y z
پارامترهای اصلاح شده خط را میتوان از پارامترهای π \pi π
Z ′ = [ sinh ( γ l ) γ l ] Z \large \boldsymbol { Z' } = \left[ \frac { \sinh ( \boldsymbol { \gamma} l ) } { \boldsymbol { \gamma } l } \right] \boldsymbol { Z } Z ′ = [ γ l sinh ( γ l ) ] Z
Y ′ 2 = [ tanh ( γ l 2 ) γ l 2 ] Y 2 \large \frac { \boldsymbol { Y' } } { 2 } = \left[ \frac { \tanh \left ( \frac { \boldsymbol { \gamma } l } {2 } \right ) } { \frac { \boldsymbol { \gamma } l } { 2 } } \right ] \frac { \boldsymbol { Y } } { 2 } 2 Y ′ = 2 γ l tanh ( 2 γ l ) 2 Y
همچنین، این پارامترها به صورت زیر نیز نوشته میشوند:
Z ′ = Z c sinh ( γ l ) \large \boldsymbol { Z' } = \boldsymbol { Z } _ { c } \sinh ( \boldsymbol { \gamma } l ) Z ′ = Z c sinh ( γ l )
Y ′ 2 = 1 Z c tanh ( γ l 2 ) \large \frac { \boldsymbol { Y' } } { 2 } = \frac { 1 }{ \boldsymbol { Z } _ { c } } \tanh \left ( \frac { \boldsymbol { \gamma } l } { 2 } \right ) 2 Y ′ = Z c 1 tanh ( 2 γ l )
اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:
^^

 نامی خط" width="363" height="177">
نامی خط" width="363" height="177">












با سلام.
استاد اگر اندازه ی ولتاژهای طرفین خط انتقال با هم برابر باشند ،خط چه حالتی پیدا می کند؟
متشکرم.