برخی پارامترهای رایج در مهندسی برق — به زبان ساده

اگر بخواهیم مدارهای الکتریکی را تحلیل کنیم، با اصطلاحاتی مانند امپدانس، مقاومت یا رزیستانس، راکتانس، ادمیتانس، ظرفیت یا کاپاسیتانس، اندوکتانس، رسانایی یا کندوکتانس، سوسپتانس و الاستانس سروکار خواهیم داشت. البته برخی از این واژه‌ها کاربرد بسیار بیشتری دارند. در مدارهای مغناطیسی نیز اصطلاحاتی مانند رلوکتانس و پرمانس وجود دارد.

در این آموزش، این اصطلاحات و تعاریف آن‌ها را بیان خواهیم کرد. همچنین، در پایان جدولی ارائه شده که همه این واژه‌ها را به‌طور خلاصه در خود جای داده است.

امپدانس (Z)

امپدانس، مخالفت کلی در برابر جریان در یک مدار الکتریکی است. این پارامتر، یک عدد مختلط است که مؤلفه حقیقی و موهومی دارد. امپدانس را با حرف بزرگ Z نمایش می‌دهند و واحد آن، اهم ($$\Omega $$) است.

امپدانس را به‌فرم مختلط زیر می‌نویسند:

$$ \Large Z = R + j X \, \, \, \, \, [ \Omega] $$

این پارامتر، مجموع مقاومت (R) و راکتانس (X) است. مقاومت، مؤلفه حقیقی امپدانس یا {Re{Z و راکتانس، مؤلفه موهومی آن یا {Im{Z است.

امپدانس را در مدار با یک بلوک مستطیلی نشان می‌دهند:

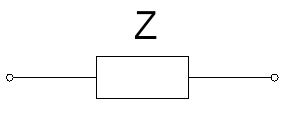
مؤلفه مقاومتی و راکتانس سلفی به‌صورت زیر نمایش داده می‌شوند:

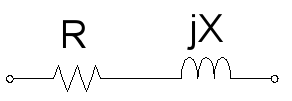
مؤلفه مقاومتی و راکتانس خازنی نیز به‌صورت زیر هستند:

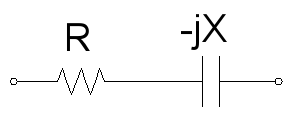
امپدانس، با استفاده از قانون اهم برای یک عنصر مدار به‌دست می‌آید:

$$ \Large Z = \frac {V } { I} \, \, \, \, \, [ \Omega ] $$

مؤلفه موهومی امپدانس، با حضور عناصری مانند سلف و خازن در مدار وجود دارد.

مقاومت (R)

مقاومت، مشابه امپدانس، وقتی ولتاژ اعمال می‌شود، با عبور جریان مخالفت می‌کند. یک امپدانس مقاومتی خالص، مؤلفه راکتیو امپدانس (سلفی یا خازنی) ندارد (مانند المنت هیتر، رادیاتور و یا مقاومت).

مقاومت را با حرف R بزرگ نشان می‌دهند و یک مقدار حقیقی دارد. واحد مقاومت، اهم ($$ \Omega $$) است.

مقاومت را در مدار با نماد زیر نمایش داده می‌شود:

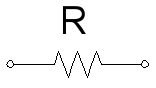
راکتانس (X)

راکتانس، بسته به اینکه با تغییر ولتاژ یا جریان مخالفت کند، دو نوع دارد.

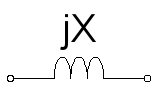
راکتانس سلفی یا القایی، با تغییر جریان مخالفت می‌کند و به‌صورت زیر نشان داده می‌شود:

راکتانس خازنی، با تغییرات ولتاژ مخالفت می‌کند و نمایش آن به‌شکل زیر است:

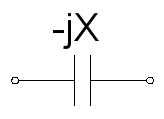
راکتانس را با حرف X بزرگ نشان می‌دهند و برابر با مؤلفه موهومی امپدانس ({Re{Z) است. بنابراین، مقدار راکتانس، یک عدد موهومی، و واحد آن اهم ($$ \Omega $$) است.

راکتانس سلفی (X_L) و اندوکتانس (L)

راکتانس سلفی، یکی از دو نوع راکتانس و یک مؤلفه امپدانس موهومی است که با تغییر جریان مخالفت می‌کند. راکتانس سلفی را با حرف X و پایین‌نویس L نشان می‌دهیم و واحد آن اهم ($$\Omega $$) است.

راکتانس سلفی، به صورت حاصل‌ضرب سرعت زاویه‌ای و اندوکتانس جسم مورد نظر محاسبه می‌شود:

$$ \Large X_ L = \omega L \, \, \, \, \, [ \Omega ] $$

که در آن، اندوکتانس بر حسب هانری (H) بیان می‌شود. فرکانس زاویه‌ای $$\omega$$ برحسب رادیان بر ثانیه است و با ضرب $$2 \pi$$ در فرکانس به‌‌دست می‌آید:

$$ \Large \omega = 2 \pi f \, \, \, \, \, [\mathrm{rad/sec}] $$

در یک مدار، راکتانس سلفی را معمولاً با یک سیم‌پیچ نشان می‌دهند، زیرا سلف‌ها معمولاً از پیچاندن یک هادی (سیم) دور یک چنبره ساخته می‌شوند.

راکتانس سلفی، همیشه یک مؤلفه امپدانس موهومی مثبت یا jX+ است.

راکتانس سلفی، از طریق تولید شار مغناطیسی، با عبور جریان مخالفت می‌کند. یک مثال خوب برای راکتانس سلفی، سیم‌پیچ ایده‌آل مانند سیم‌پیچی در استاتور یک موتور یا ژنراتور است.

راکتانس خازنی (X_C) و ظرفیت (C)

راکتانس خازنی، یکی از دو نوع راکتانس و یک مؤلفه امپدانس موهومی است که با تغییر ولتاژ‌ مخالفت می‌کند. این پارامتر را با X بزرگ و پایین‌نویس C نشان می‌دهند و برحسب اهم ($$\Omega$$) بیان می‌کنند.

راکتانس خازنی، برابر با معکوس حاصل‌ضرب فرکانس زاویه‌ای و ظرفیت جسم مورد نظر است:

$$ \Large X_C = \frac {1} { \omega C } \, \, \, \, \, [\Omega ] $$

که در آن، ظرفیت برحسب فاراد (F) اندازه‌گیری می‌شود:

$$ \Large C \, \, \, \, \, [\mathrm{F}] $$

فرکانس زاویه‌ای $$\omega$$ برحسب رادیان بر ثانیه است و با ضرب $$2 \pi$$ در فرکانس به‌‌دست می‌آید:

$$ \Large \omega = 2 \pi f \, \, \, \, \, [\mathrm{rad/sec}] $$

در نمودار مدارها، معمولاً راکتانس خازنی را با نماد خازن نشان می‌دهند، زیرا معمولاً خازن‌ها از دو صفحه هادی مجزا تشکیل می‌شوند که با یک دی‌الکتریک جدا شده‌اند.

راکتانس خازنی، در مقابل ولتاژ ناشی از بارهای بین دو صفحه هادی مقاومت می‌کند. این پارامتر، همیشه یک مؤلفه امپدانس موهومی یا jX- است.

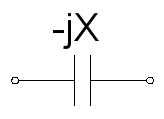
یک مثال از راکتانس خازنی خالص، خازن ایده‌آل کامل است.

ادمیتانس (Y)

ادمیتانس، معکوس امپدانس است و میزان سهولت در عبور جریان را در اثر اعمال ولتاژ نشان می‌دهد. ادمیتانس را با حرف بزرگ Y نشان می‌دهند و واحد آن، زیمنس (S) است. این پارامتر، در حالت کلی یک عدد مختلط است و به‌فرم زیر نوشته می‌شود:

$$ \Large Y = G + j B \, \, \, \, \, [ \mathrm{S}] $$

که مجموع رسانایی (G) و سوسپتانس (B) است.

رسانایی، مؤلفه حقیقی ادمیتانس ({Re{Y) و سوسپتانس مؤلفه موهومی آن ({Im{Y) است. ادمیتانس را می‌توان با عکس کردن امپدانس محاسله کرد:

$$ \Large Y =  \frac{1} {Z} \,\,\,\, [\mathrm {S}] $$

قانون اهم برحسب ادمیتانس، ولتاژ و جریان به‌صورت‌های زیر بیان می‌شود:

$$ \Large V = \frac{I } {Y } \, \, \, \, \, [\mathrm{V}] $$

$$ \Large I =  { V } {Y } \, \, \, \, \, [\mathrm{A}] $$

رسانایی (G)

مفهوم رسانایی یا کندوکتانس، در برابر مقاومت قرار می‌گیرد و مؤلفه حقیقی ادمیتانس ({Re{Y) است و به همین دلیل، یک عدد مختلط نیست. رسانایی را با حرف بزرگ G نشان می‌دهند و واحد آن، زیمنس (S) است.

اگر امپدانس مؤلفه موهومی نداشته باشد و مقاومت خالص داشته باشیم، رسانایی را می‌توان از روی معکوس مقاومت به‌دست آورد:

$$ \Large G = \frac{ 1} { R } \, \, \, \, \, [\mathrm{S}] $$

سوسِپتانس (B)

سوسپتانس، از نظر مفهومی در مقابل راکتانس قرار می‌گیرد و مؤلفه موهومی ادمیتانس ({Img{Y) است. سوسپتانس را با حرف بزرگ B نشان می‌دهند و واحد آن، زیمنس (S) است.

اگر امپدانس، موهومی خالص باشد و مؤلفه حقیقی نداشته باشیم، سوسپتانس را می‌توان با معکوس کردن راکتانس به‌دست آورد:

$$ \Large B = \frac{ 1} { X } \, \, \, \, \, [\mathrm{S}] $$

سوسپتانس، میزان سهولت در تغییر جریان یا ولتاژ مدار را نشان می‌دهد.

الاستانس (S)

الاستانس با نماد $$S$$، معکوس ظرفیت و واحد آن «فارادمعکوس» ($$ F ^ { – 1 } $$) است (فارادمعکوس، گاهی داراف (Daraf) نیز نامیده می‌شود). اصطلاح الاستانس به‌ندرت مورد استفاده قرار می‌گیرد.

دو کمیت دیگر نیز وجود دارند که در مدارهای مغناطیسی به‌کار می‌روند.

رلوکتانس

رلوکتانس (R) یا مقاومت مغناطیسی، کمیتی است که در مدارهای مغناطیسی، میزان مخالفت مدار را در برابر عبور شار مغناطیسی نشان می‌دهد. رلوکتانس معادل مدار مغناطیسی برابر با نسبت نیروی محرکه مغناطیسی به شار مغناطیسی آن است.

پرمانس

معکوس رلوکتانس را پرمانس (P) یا هدایت مغناطیسی می‌نامند که نشان‌دهنده میزان سهولت عبور شار است.

جمع‌بندی

پارامترها و واحدهای آن‌ها،  در جدول زیر خلاصه شده است.

اگر این مطلب برای شما مفید بوده است و علاقه‌مند به یادگیری مباحث مشابه هستید، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های مهندسی برق
• مجموعه آموزش‌های نرم‌افزارهای برق و الکترونیک
• مجموعه آموزش‌های دروس مهندسی برق
• آموزش مدارهای الکتریکی 1
• مدارهای جریان مستقیم (DC) — به زبان ساده
• دوقطبی در مدارهای الکتریکی — به زبان ساده

^^