اندوکتانس سیم پیچ — به زبان ساده (+ دانلود فیلم آموزش رایگان)

در این آموزش درباره محاسبه اندوکتانس سیم پیچ یا سلف بحث خواهیم کرد. از مفاهیم الکترومغناطیس می‌دانیم که با تغییر میدان مغناطیسی یک سیم‌پیچ‌، «نیرو محرکه الکتریکی» (Electromotive Force) یا EMF درون آن القا خواهد شد. اگر نیرو محرکه الکتریکی القا شده در سیم‌پیچ به دلیل تغییر جریان گذرنده از آن به وجود بیاید، به آن «خود القایی» (Self-Induction) می‌گویند. به دلیل اینکه در این حالت، پلاریته ولتاژ تولید شده معکوس است، به آن «نیرو محرکه الکتریکی معکوس» (Back-EMF) نیز گفته می‌شود.

تعریف اندوکتانس سیم پیچ

زمانی که نیرو محرکه الکتریکی درون یک سیم به واسطه تغییر میدان مغناطیسی القا شده در سیم مجاور باشد، «القای متقابل» (Mutual-Induction) به وجود می‌آید. القای متقابل اساس کار ترانسفوروماتورها، موتورها، رله‌های الکتریکی و ... را تشکیل می‌دهد. خود القایی، حالتی خاص از القای متقابل است که درون یک مدار ایزوله اتفاق می‌افتد و عموما به آن اندوکتانس (Inductance) می‌گویند.

فیلم آموزش مبانی مهندسی برق ۲ – مرور و حل تمرین در فرادرس

کلیک کنید

واحد اندازه‌گیری اندوکتانس، به افتخار «جوزف هانری» (Joseph Henry)، هانری (H) نامگذاری شده است. یک هانری، برابر با یک وبر بر آمپر ($$1H=1Wb/A$$) است.

با توجه به قانون لنز می‌دانیم که نیرو محرکه القایی باعث به وجود آمدن یک جریان خواهد شد. بر اساس قانون کنش و واکنش، این جریان با تغییرات شار الکتریکی که باعث تولید نیرو محرکه الکتریکی القایی شده است مخالفت می‌کند. بنابراین اگر بخواهیم تعریف دقیقی از اندوکتانس ارائه دهیم، می‌توان گفت: «زمانی که تغییر جریان سیم‌پیچ به اندازه یک آمپر بر ثانیه باعث القا شدن یک نیرو محرکه الگتریکی یک ولتی در سیم‌پیچ شود، اندوکتانس آن سیم‌پیچ یک هانری خواهد بود».

به عبارت دیگر، زمانی که جریان عبوری از سیم‌پیچ با سرعت یک آمپر بر ثانیه (A/s) تغییر کند، اندوکتانس سیم‌پیچ یک هانری ($$ 1 \, \text{H} $$) است. این تغییر باعث القا شدن ولتاژی به اندازه یک ولت در سیم‌پیچ می‌شود. بنابراین، نمایش ریاضی تغییر جریان سیم‌پیچ بر حسب زمان به صورت زیر است:

$$\large \frac{di}{dt} \left(A/s\right)$$

که در آن، $$di$$ تغییرات جریان بر حسب آمپر و $$dt$$ مدت زمان این تغییرات بر حسب ثانیه است. بنابراین، ولتاژ القا شده در یک سیم‌پیچ ($$ V_L$$) با اندوکتانس $$L$$ به صورت زیر است:

$$\large V_L = -L\frac{di}{dt} \left(V\right)$$

باید دقت کرد که علامت منفی نشان می‌دهد که ولتاژ القا شده مخالف تغییرات جریان سیم‌پیچ در واحد زمان ($$\frac{di}{dt}$$) است.

به توجه به معادله بالا، اندوکتانس یک سیم‌پیچ به صورت زیر محاسبه می‌شود:

$$\large L=\frac{V_L}{di/dt} = \frac{1volt}{1A/s}=1 Henry$$

که در آن، $$L$$ اندوکتانس بر حسب هانری، $$V_L$$ ولتاژ عبوری از سیم‌پیچ و $$di/dt$$ تغییرات جریان بر حسب آمپر بر ثانیه است.

اندوکتانس، در واقع نشان دهنده مقاومت سلف نسبت به تغییر جریان درون آن است. هرچه مقدار اندوکتانس (هانری) سلف بیشتر باشد، نرخ تغییرات جریان آن نیز کمتر است و هرچه مقدار اندوکتانس یک سلف کمتر باشد، نرخ تغییرات جریان آن بیشتر خواهد بود.

همانطور که می‌دانیم، سلف‌ها انرژی را به صورت میدان مغناطیسی در خود ذخیره می‌کنند. سلف‌ها از یک سیم پیچیده شده به دور یک هسته ساخته می‌شوند. هرچه تعداد دور سیم بیشتر باشد، به ازای اعمال یک جریان یکسان، شار مغناطیسی قوی‌تری تولید خواهد شد.

بنابراین، با افزایش تعداد دور سیم‌پیچ، اندوکتانس آن افزایش می‌یابد. رابطه بین خودالقایی ($$L$$) و تعداد دور ($$N$$) در سیم‌پیچ به صورت زیر است:

 $$\large L=N\frac{\Phi}{I}$$

که در آن، $$L$$ بر حسب هانری، $$N$$ تعداد دورها،  $$\Phi$$ شار مغناطیسی و $$I$$ جریان بر حسب آمپر است.

همچنین، این فرمول را می‌توان به صورت پیوند شار مغناطیسی ($$N\Phi$$) تقسیم بر جریان در نظر گرفت؛ با این فرض که مقدار جریان ثابتی از هر دور سیم‌پیچ عبور می‌کند. باید دقت کرد که این فرمول تنها در مورد مواد مغناطیسی خطی به کار می‌رود.

مثال ۱

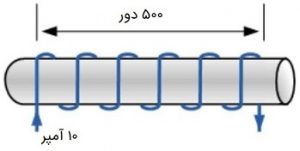
یک هسته توخالی را در نظر بگیرید که یک سیم مسی 500 بار دور آن پیچانده شده است. زمانی که جریانی $$DC$$ به اندازه 10 آمپر از سیم‌پیچ عبور می‌کند، شار مغناطیسی  $$10mWb$$ تولید می‌شود. خودالقایی سیم‌پیچ را بر حسب میلی‌هانری محاسبه کنید.

حل:

$$\large L=N\frac{\Phi}{I}=500\frac{0.01}{10}=500mH $$

خودالقایی یک سیم‌پیچ یا به طور دقیق‌تر، ضریب خودالقایی سیم‌پیچ، به ویژگی‌های ساخت (برای مثال اندازه، طول، تعداد دورهای سیم‌پیچ و...) آن بستگی دارد. بنابراین، با استفاده از هسته‌ای با ضریب نفوذ بالا و تعداد دور زیاد، امکان ساخت اندوکتانس با ضریب خودالقایی بالا نیز ممکن است. شار مغناطیسی که در هسته داخلی یک سیم‌پیچ ایجاد می‌شود برابر است با:

$$\large \Phi=‌B.A$$

که در آن $$\Phi$$ شار مغناطیسی، $$B$$ چگالی شار و $$A$$ مساحت مقطع هسته است.

اگر سیم‌پیچ، یک سلونوئید بلند با تعداد $$N$$ دور در هر متر فضای آزاد (هوا) باشد، القای مغناطیسی درون هسته به صورت زیر است:

$$\large B=\mu_0H=\mu_0\frac{N.I}{\ell}$$

بنابراین، با جایگزینی عبارت بالا در $$ \Phi=‌B.A$$ داریم:

$$\large L=\mu_0 \frac{N^{2}.A}{\ell}$$

که در آن، $$L$$ بر حسب هانری، $$\mu_0$$ ضریب نفوذپذیری فضای آزاد $$ \left(4 \times \pi \times 10^{-7}\right)$$، $$N$$ تعداد دورها، $$A$$ مساحت سطح مقطع هسته $$ \left(\pi r^{2}\right)$$ بر حسب متر مربع و $$l$$ طول هسته بر حسب متر است.

از آنجایی که اندوکتانس سیم‌پیچ به دلیل شار مغناطیسی اطراف آن ایجاد شده است، هرچه شار مغناطیسی برای یک مقدار مشخصی از جریان، بزرگتر باشد، اندوکتانس نیز بیشتر خواهد شد. بنابراین، یک سیم‌پیچ با تعداد دور بیشتر، اندوکتانس بزرگتری نسبت به همان سیم‌پیچ با تعداد دور کمتر دارد. این قانون در فرمول بالا با مقدار $$N^{2}$$ نشان داده شده است. مشاهده می‌شود که اندوکتانس با مجذور تعداد دور سیم‌پیچ رابطه مستقیم دارد.

فیلم آموزش مروری ماشین های الکتریکی ۱ در فرادرس

کلیک کنید

برای افزایش اندوکتانس، علاوه بر زیاد کردن تعداد دور سیم‌پیچ، می‌توان از افزایش قطر سیم‌پیچ یا کم کردن طول هسته استفاده کرد.

اگر هسته داخلی سیم‌پیچ از مواد فرومغناطیسی مانند آهن نرم، کبالت یا نیکل ساخته شود، اندوکتانس سیم‌پیچ نسبت به هسته هوا بیشتر خواهد بود. از آنجایی که این مواد، خطوط نیرو را از طریق هسته نرم فرومغناطیسی متمرکزتر خواهند کرد، با اعمال جریان یکسان به سیم‌پیچ، شار مغناطیسی بسیار بیشتری تولید می‌کنند.

برای مثال، اگر ضریب نفوذپذیری نسبی ماده به کار رفته در هسته، ۱۰۰۰ برابر بزرگتر از هوی آزاد باشد ($$ 1000 \mu _ 0 $$)، اندوکتانس سیم‌پیچ ۱۰۰۰ برابر بزرگتر خواهد بود. بنابراین، می‌توان گفت که اندوکتانس یک سیم‌پیچ متناسب با ضریب نفوذپذیری هسته است. بنابراین در فرمول اندوکتانس که در بالا گفته شد، باید به جای $$\mu_0$$، ضریب نفوذپذیری جنس هسته سیم‌پیچ ($$\mu_r$$) را قرار دهیم.

اگر سیم‌پیچ بر روی یک هسته با جنس فرومغناطیس پیچیده شود، از آنجایی که ضریب نفوذپذیری آن با چگالی شار تغییر خواهد کرد، اندوکتانس افزایش می‌یابد. البته، بر حسب نوع ماده فرومغناطیسی به کار رفته، ممکن است شار مغناطیسی هسته داخلی سریعا به اشباع برسد. در این حالت، اندوکتانس به صورت غیر خطی تولید خواهد شد. از آنجایی که چگالی شار اطراف سیم‌پیچ به جریان عبوری از آن بستگی دارد، اندوکتانس ($$L$$) تابعی از این جریان ($$i$$) است.

در آموزش بعدی در مورد سلف‌ها، خواهیم دید که میدان مغناطیسی تولید شده توسط یک سیم‌پیچ می‌تواند باعث ایجاد جریان در سیم‌پیچ مجاور شود. این اثر را «القای متقابل» (Mutual-Induction) می‌گویند. القای متقابل اساس کار ترانسفورماتورها، موتورها و ژنراتورها است.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های مهندسی برق
• آموزش ماشین های الکتریکی ۱
• مجموعه آموزش‌‌های مهندسی قدرت
• آموزش الکترومغناطیس مهندسی
• مغناطیس چیست؟ — به زبان ساده
• مدارهای مغناطیسی — به زبان ساده
• آشنایی با ترانسفورماتورها — مجموعه مقالات جامع وبلاگ فرادرس

^^