سلف یا القاگر چیست؟ — به زبان ساده (+ دانلود فیلم آموزش رایگان)

در آموزشهای قبلی مجله فرادرس درباره الکترومغناطیس، دیدیم که وقتی جریان الکتریکی از یک سیم رسانا عبور کند، یک شار مغناطیسی در اطراف آن تشکیل میشود. این اثر، رابطهای بین جهت شار مغناطیسی (که در اطراف سیم وجود دارد) و جهت جریان گذرنده از سیم ایجاد میکند که از قانون دست راست حاصل میشود. در این آموزش، با سلف یا القاگر آشنا میشویم.
سلف یا القاگر
اما ویژگی مهم دیگری نیز مربوط به یک «پیچه» (Coil) وجود دارد و آن این است که در اثر شار مغناطیسی، ولتاژ ثانویهای در آن القا میشود که در برابر هرگونه تغییر جریان الکتریکی گذرنده از آن مقاومت یا مخالفت میکند.
یک سلف یا القاگر (Inductor)، در سادهترین شکل خود، چیزی جز یک سیمپیچ حول یک هسته مرکزی نیست. در اغلب پیچهها، جریان گذرنده از سیمپیچی، شار مغناطیسی را تولید میکند که متناسب با جریان گذرنده از آن است.
سلف که گاهی «چوک» (Choke) نیز نامیده میشود، یک قطعه الکتریکی پسیو است که از یک پیچه سیمی تشکیل شده است.

سلفها از یک سیمپیچی محکم به دور یک هسته مرکزی جامد ساخته میشوند. هسته میتواند به شکل استوانه یا یک چنبره باشد که به دور آن سیم پیچانده شده است تا شار مغناطیسی را درون حلقه خود متمرکز کند.
نماد شماتیکی سلف، یک پیچه از سیم است. بنابراین، میتوان یک پیچه از سیم را یک القاگر یا سلف دانست. سلفها را معمولاً بر اساس نوع هسته داخلی که به دور آن سیم پیچانده شده است دستهبندی میکنند. برای مثال: هسته خالی (هوا)، هسته آهن سخت یا هسته فریت نرم. این نوع هستهها با دو خط موازی ممتد یا منقطع در کنار نماد اصلی سلف نشان داده میشوند. شکل زیر این موضوع را نشان میدهد.
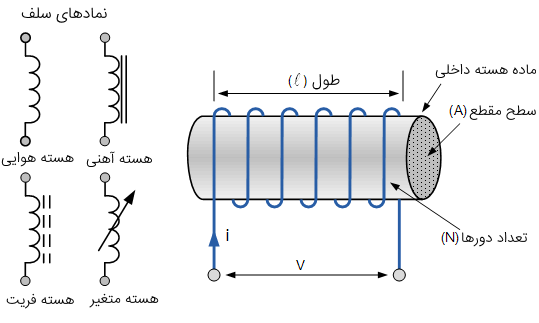
وقتی جریان از سلف میگذرد، یک شار مغناطیسی تولید میشود که متناسب با این جریان است. اما برخلاف خازن که در برابر تغییر ولتاژ صفحات مخالفت میکند، سلف در برابر تغییر جریان گذرنده از سیم مخالفت میکند.
به عبارت دیگر، سلفها در برابر تغییرات جریان مخالفت یا مقاومت میکنند، اما در حالت ماندگار ، به سادگی جریان را از خود عبور میدهند. این قابلیت سلف در مقاومت در برابر تغییرات جریان که آن را به شار پیوندی مغناطیسی مرتبط میکند، «اندوکتانس» (Inductance) نام دارد و با نماد نشان داده میشود. واحد اندوکتانس، هانری () است و به افتخار «جوزف هانری» (Joseph Henry) نامگذاری شده است.
از آنجایی که هانری واحد نسبتاً بزرگی برای اندوکتانس است، از زیرواحدهای هانری برای بیان اندازه اندوکتانس سلفها استفاده میشود. جدول زیر این موضوع را نشان میدهد.
| پیشوند | نماد | ضریب | به توان ۱۰ |
| میلی | |||
| میکرو | |||
| نانو |
بنابراین، یا میلیهانری، برابر با یکهزارم هانری است.
سلفها یا پیچهها، قطعات الکتریکی بسیار رایج و پرکاربردی هستند و عوامل زیادی مانند شکل پیچه، تعداد دور سیم، تعداد لایههای سیم، فاصله بین دورها، نفوذپذیری ماده هسته، اندازه سطح مقطع هسته و... در تعیین مقدار اندوکانس آنها تأثیر دارند.
فرض کنید یک سلف، سطح مقطع و تعداد دور ثابتی در طول واحد دارد. اگر شار مغناطیسی ، مقدار دور از سیمپیچی دور هسته را احاطه کند، شار پیوندی را خواهیم داشت و هر جریان که از آن بگذرد، یک شار مغناطیسی در خلاف جهت جریان القا خواهد کرد. در نتیجه، بر اساس قانون فارادی، هر تغییری در این شار مغناطیسی پیوندی، یک ولتاژ خودالقایی تولید خواهد کرد که برابر است با:
که در آن:
- تعداد دورها
- مساحت سطح مقطع هسته بر حسب متر مربع
- مقدار شار بر حسب وبر
- نفوذپذیری ماده هسته
- طول پیچه بر حسب متر
- و نرخ تغییر جریان بر حسب آمپر بر ثانیه است.
یک میدان مغناطیسی متغیر با زمان، ولتاژی را القا میکند که متناسب با نرخ تغییر جریان است. اگر این ولتاژ مثبت باشد، نشان دهنده افزایش نیروی محرکه الکتریکی (EMF) است و اگر منفی باشد، کاهش آن را نشان میدهد. معادله مربوط به ولتاژ خودالقایی، جریان و اندوکتانس را میتوان با تعویض با بازنویسی کرد. همانطور که گفتیم، پارامتر ثابت تناسب بین ولتاژ و تغییرات جریان است و اندوکتانس پیچه نامیده میشود.
رابطه بین شار سلف و جریان گذرنده از آن، به صورت است. از آنجایی که سلف از یک پیچه متشکل از سیم هادی تشکیل شده است، به معادله اخیر برای نیروی محرکه الکتریکی خودالقایی میرسیم که گاهی ولتاژ ضدمحرکه الکتریکی (Back EMF) القایی پیچه نامیده میشود:
که در آن، اندوکتانس خودی و نرخ تغییر جریان است.
بنابراین، با توجه به معادله اخیر میتوان گفت که EMF خودالقایی برابر است با حاصلضرب اندوکتنس در نرخ تغییر جریان. وقتی اندوکتانس مدار یک هانری است که جریانی با نرخ تغییر یک آمپر بر ثانیه از آن بگذرد و به اندازه یک ولت EMF در مدار القا شود.
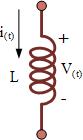
یک نکته مهم این است که معادله مربوط به EMF، ناشی از تغییر جریان است، زیرا اگر جریان عبوری از سلف ثابت باشد و تغییری نکند، مانند یک جریان حالت ماندگار DC ولتاژ EMF القایی برابر با صفر خواهد بود. زیرا در این حالت نرخ لحظهای تغییر جریان برابر با صفر است: .
با عبور یک جریان DC حالت ماندگار و در نتیجه ولتاژ القایی صفر، سلف مانند یک اتصال کوتاه و در واقع، یک سیم عمل خواهد کرد یا نهایتاً مقاومت بسیار کمی خواهد داشت. به عبارت دیگر، مخالفت سلف با عبور جریان در مدارهای AC و DC بسیار متفاوت است.
ثابت زمانی سلف
جریان یک سلف نمیتواند به طور ناگهانی تغییر کند، زیرا در این صورت، در مدت زمان صفر، جریان به اندازه محدودی تغییر میکند و در نتیجه نرخ تغییر جریان بینهایت خواهد شد: . در این صورت، EMF القایی نیز بینهایت خواهد بود که میدانیم ولتاژ بینهایت وجود ندارد. البته اگر جریان عبوری از سلف بسیار سریع تغییر کند (مانند مدت زمان عملکرد یک کلید)، ولتاژهای بالایی میتواند در سلف القا شود.
مدار سلف شکل زیر را در نظر بگیرید. وقتی کلید باز است، جریانی از سیمپیچ سلف عبور نمیکند. اگر جریانی از سلف نگذرد، نرخ تغییر جریان سیمپیچ نیز برابر با صفر خواهد بود و اگر نرخ تغییر جریان برابر با صفر باشد، EMF خودالقایی نیز برابر با صفر است.
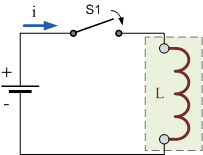
اکنون فرض کنید در لحظه کلید را ببندیم. در این صورت، جریان در مدار برقرار میشود و به آرامی افزایش مییابد تا به حداکثر مقدار خود برسد. این مقدار حداکثر را اندوکتانس سلف تعیین میکند.
نرخ تغییر جریان گذرنده از سلف، در مقدار اندوکتانس سلف ضرب میشود و مقدار ولتاژ القایی ثابت تولیدی در دو سر سیمپیچ را نتیجه میدهد:
این مقدار EMF القایی دو سر پیچه () تا زمانی که جریان به مقدار حداکثر خود برسد و حالت ماندگار برقرار شود، در برابر ولتاژ القایی مقابله خواهد کرد.
جریانی که در این حالت در مدار وجود دارد، تنها با مقدار مقاومت DC یا خالص تعیین میشود، زیرا به دلیل صفر بودن تغییرات جریان در حالت ماندگار، مقدار راکتانس سیمپیچ به صفر کاهش مییابد. به عبارت دیگر، در حالت ماندگار، فقط مقاومت DC برای مخالفت با عبور جریان وجود دارد.
به طور مشابه، اگر کلید باز شود، جریان گذرنده از سیمپیچ شروع به کاهش میکند، اما سلف، مانند قبل در برابر تغییر مخالفت خواهد کرد و تلاش میکند از طریق القای ولتاژ در جهت مخالف، جریان گذرنده از سیمپیچ را در مقدار قبلی نگه دارد.
شیب کاهش جریان، منفی خواهد بود و مطابق شکل زیر با اندوکتانس سیمپیچ ارتباط خواهد داشت.
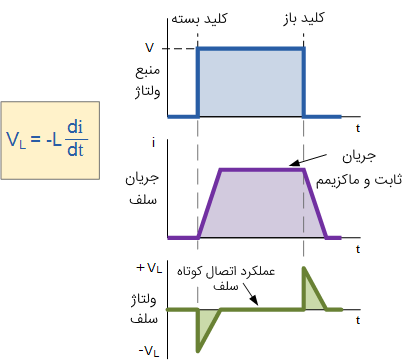
مقدار ولتاژ القایی تولیدی توسط سلف، به نرخ تغییر جریان بستگی دارد. در آموزش القای فارادی، گفتیم که طبق قانون لنز، «جهت EMF القایی همواره به گونهای است که با تغییرات به وجود آورنده خود مخالفت میکند». به عبارت دیگر، یک EMF القایی، همیشه مخالف حرکت یا تغییری است که آن را به وجود آورده است.
بنابراین، با کاهش جریان، پلاریته ولتاژ بهگونهای خواهد بود که به عنوان منبع عمل کند و با افزایش جریان، پلاریته ولتاژ مانند یک بار خواهد بود. برای یک نرخ تغییر جریان مشابه در سیمپیچ، افزایش یا کاهش اندازه EMF القایی مشابه خواهد بود.
مثال
در حالت ماندگار، جریان مستقیم آمپر از یک سلونوئید میگذرد که اندوکتانس آن است. مقدار ولتاژ ضدمحرکه القایی سیمپیچ را به گونهای به دست آورید که کلید مدار شکل بالا، به مدت باز بوده و جریان گذرنده از آن به صفر آمپر رسیده باشد.
حل:
توان سلف
همانطور که میدانیم، سلف در مدار با عبور جریان مخالفت میکند، زیرا گذر جریان سبب القای یک EMF میشود که طبق قانون لنز با آن مخالفت میکند. در نتیجه، منبع باتری خارجی کار انجام میدهد تا جریان گذرنده مخالف با EMF القایی را نگه دارد. توان لحظهای سلف به صورت زیر به دست میآید:
یک سلف ایدهآل مقاومت ندارد () و تنها اندوکتانس دارد. در نتیجه، توانی در سیمپیچ تلف نمیشود. بنابراین میتوان گفت که در یک سلف ایدهآل، تلفات توان صفر است.
انرژی یک سلف
وقتی توان در سلف شارش میکند، انرژی در میدان مغناطیسی آن ذخیره میشود. هنگامی که جریان گذرنده از سلف افزایش یابد و مثبت باشد، توان لحظهای مدار نیز بزرگتر از صفر است (). علامت مثبت یعنی انرژی در سلف ذخیره میشود.
به طور مشابه، اگر جریان گذرنده از سلف کاهشی باشد ()، توان باید کوچکتر از صفر بوده و در این صورت، انرژی سلف به مدار بر میگردد.
با استفاده از معادله توان بالا، انرژی مغناطیسی که مثبت است و در سلف ذخیره میشود، برابر است با:
که در آن بر حسب ژول، بر حسب هانری و بر حسب آمپر است.
در حقیقت، با عبور جریان از سلف، انرژی در میدان مغناطیسی اطراف آن ذخیره میشود. در یک سلف ایدهآل، مقاومت یا ظرفیت خازنی وجود ندارد و انرژی جریان بدون تلفات در سلف ذخیره میشود. زمانی که جریان کاهش یافته و میدان کم شود، مقدار انرژی نیز کاهش مییابد.
در یک مدار AC، سلف به صورت متناوب انرژی را در هر چرخه ذخیره میکند و تحویل میدهد. اگر جریان گذرنده از سلف، مانند مدار DC ثابت باشد، آنگاه تغییری در انرژی ذخیره شده رخ نمیدهد، زیرا .
بنابراین، سلف را میتوان به عنوان یک قطعه پسیو در نظر گرفت، زیرا انرژی را در مدار هم ذخیره میکند و هم تحویل میکند، اما نمیتواند آن را تولید کند. یک سلف ایدهآل، بدون تلفات است؛ به این معنی که انرژی را به طور نامحدود ذخیره میکند و آن را تلف نمیکند. البته سلفهای واقعی، همیشه مقداری مقاومت دارند که بدون توجه به متناوب یا ثابت بودن جریان، طبق قانون اهم () توانی را به شکل گرما تلف میکنند.
کاربرد اولیه سلفها در مدارهای فیلتر کننده، مدارهای تشدید و نیز محدود کردن جریان است. از یک سلف میتوان برای مسدود کردن یا تغییر شکل موج جریان متناوب یا محدودهای از فرکانسهای سینوسی استفاده کرد و در این حالت، از سلف برای تنظیم یک گیرنده رادیویی ساده یا انواع مختلف اسیلاتورها استفاده میشود. همچنین یک سلف میتواند در برابر تغییرات ولتاژ مخرب و جریانخای هجومی بالا، از تجهیزات حساس محافظت کند.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- تزویج در مدارهای الکتریکی — مفاهیم اصلی
- مدارهای مغناطیسی — به زبان ساده
- آشنایی با ترانسفورماتورها — مجموعه مقالات جامع وبلاگ فرادرس
^^













سلام شار مغناطیسی عبوری در سیملوله (القاگر) به تعداد دور بستگی دارد یا خیر؟
با سلام خدمت شما؛
بله شار مغناطیسی عبوری از سیملوله، به تعداد دورهای سیم نیز بستگی دارد، اما این وابستگی در قدرت میدان مغناطیسی نهفته است. چون در فرمول شار مغناطیسی، وابستگی مستقیمی به N یعنی تعداد دورهای سیم وجود ندارد. اگر به فرمول شار مغناطیسی دقت کنید، این رابطه برابر است با حاصلضرب میدان مغناطیسی در مساحت سطح موردنظر. با افزایش تعداد سیمها در سیملوله، قدرت میدان زیاد شده و در نتیجه شار مغناطیسی هم افزایش خواهد یافت.
از همراهی شما با مجله فرادرس سپاسگزاریم.
سلام وقت بخیر سپاس بابت مطالب ارزندتون
امکانش هست از طریق ایمیل یک بررسی راجب مغناطیس باهم انجام بدیم
پیشاپیش از حسن توجه شما سپاسگزارم
لطفاً یه مثال از حل مقدار سلف بزنید با فریت یا هسته هوا تیرویید
خیلی مفید و کامل توضیح داده شده واقن از خیلی کلاس های دانشگاه که دارن مدار یا الکترونیک تدریس میکنن بهتر گفته شده
سلام صابر عزیز.
از اینکه این آموزش برایتان مفید بوده است، بسیار خوشحالیم.
شاد و پیروز باشید.
سلام
من بعنوان یک دبیر فیزیک آزمایشگاه از مطالب ارائه شده و نحوه تدریس آن خیلی استفاده بردم.
با تشکر از مدرس محترم جناب سید سراج حمیدی
عالی و مفید بود، استفاده کردم، فقط نمیدونم چرا ویدیو دوم دقیقه 5 و ویدیو سوم دقیقه یک قطع میشه، اشکال دارن فک کنم
سلام، وقت شما بخیر؛
از بابت گزارش شما درباره اشکال ویدیوهای این مطلب ممنونیم. ویدیوهای مذکور مورد بازبینی قرار گرفتند و اشکالی که در نمایش آنها وجود داشت رفع شده است.
از همراهی شما با مجله فرادرس بسیار سپاسگزاریم.