امپدانس و محاسبه آن – به زبان ساده (+ دانلود فیلم آموزش رایگان)

احتمالاً بارها به واژه امپدانس به هنگام مطالعه فیزیک الکتریسیته و مباحث مهندسی برق برخورده‌اید. اگر تا امروز معنی و مفهوم این واژه برایتان نا‌آشنا است، با ما در ادامه این مقاله همراه باشید تا با زبانی ساده، به تعریف امپدانس و نحوه محاسبه آن بپردازیم.

در مقاله «خازن در جریان متناوب -- به زبان ساده» دیدیم عنصر خازن، هنگامی که در مداری با جریان متناوب قرار گیرد، از خود مقاومتی واکنشی موسوم به «راکتانس» (Reactance) نشان می‌دهد. این امر برای عنصر پسیو سلف نیز صادق است. پس به طور خلاصه برای مداری با ۳ عنصر پسیو خازن (Capacitor)، سلف (Icanductor) و مقاومت (Resistor) در جریان متناوب، با سه مقاومت متفاوت، به نام‌های راکتانس خازنی ($$X_{C}$$)، راکتانس سلفی ($$X_{L}$$) و مقاومت عادی ($$R$$) روبه‌رو هستیم. دقت شود که در جریان ثابت ($$DC$$) مقاومت واکنشی (راکتانس) عناصر خازن و سلف صفر بوده و مقاومت مدار تنها ناشی از عنصر مقاومت ($$R$$) است. البته برای خازن بهتر است که بگوییم راکتانس در جریان ثابت بی‌نهایت است، به همین دلیل هنگامی که خازن در جریان ثابت پر می‌شود، دیگر جریان را از خود عبور نمی‌دهد. اما معمولاً در جریان‌های ثابت راکتانس را تعریف نمی‌کنند.

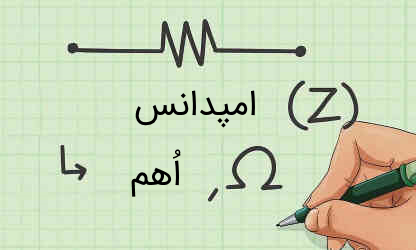
واژه «امپدانس» (Impedance) به مقاومتی که یک عنصر یا مدار به هنگام عبور جریان متناوب از خود نشان می‌دهد، اشاره دارد. در واقع امپدانس واژه‌ای کلی‌تر از مقاومت بوده و در یک مدار به مجموع راکتانس‌ خازنی و سلفی و مقاومت R، امپدانس گفته می‌‌شود. بدیهی است که واحد سنجش امپدانس، «اُهم» (Ohm) با نماد Ω است. محاسبه امپدانس، کار دشواری نبوده و تنها از یک رابطه ساده به دست می‌آید. جهت بررسی بیشتر در ادامه این مقاله همراه ما باشید.

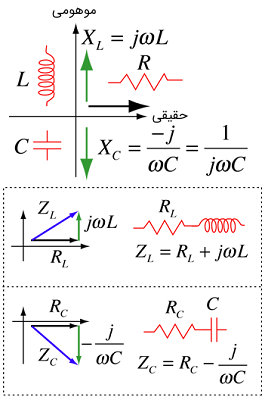
امپدانس

همان‌طور که در مقدمه متن اشاره کردیم، امپدانس که آن را با نماد $$Z$$ نشان می‌دهند، مقاومت مدار در برابر شارش یا عبور الکترون‌ها (جریان الکتریکی) است. دو عامل مختلف باعث کند شدن جریان در مدار شده که هر دوی این عوامل (مقاومت) در مقدار امپدانس موثر هستند.

اولین عامل مقاومت عادی ($$R$$) عناصر است و مربوط به ساختار ماده می‌شود. عامل دوم راکتانس ($$X$$) بوده که ناشی از وجود میدان‌های الکتریکی و مغناطیسی در خازن و سلف به هنگام عبور جریان الکتریکی متناوب ($$AC$$) است. قابل از اینکه به رابطه اصلی برای محاسبه امپدانس بپردازیم، بهتر است که مروری بر مقاومت عادی ($$R$$) و مقاومت واکنشی (راکتانس - $$X$$) داشته باشیم.

 مقاومت (Resistance)

در فیزیک پایه، هنگام مطالعه قانون اُهم با پارامتر مقاومت آشنا شدید. قانون ساده اُهم به رابطه اختلاف پتانسیل بین دو سر عنصر مقاومتی و جریان الکتریکی گذرنده از آن می‌پردازد. واحد سنجش مقاومت، ولت بر آمپر ($$\frac{V}{A}$$) یا اُهم با نماد Ω است.

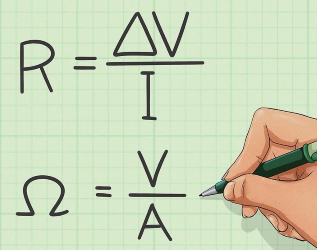
مقاومت مانع از عبور جریان الکتریکی (الکترون‌های آزاد) می‌شود. به یاد داشته باشید که مقاومت ($$R$$) برای عنصر پسیو مقاومت، در هر دو جریان الکتریکی $$DC$$ و $$AC$$ وجود داشته و مقدار آن در هر دو جریان یکسان است.

راکتانس (Reactance)

راکتانس مقاومتی است که عناصر پسیو خازن و سلف به هنگام عبور جریان الکتریکی متناوب ($$AC$$) از خود نشان می‌دهند. به یاد داشته باشید که در جریان‌های الکتریکی ثابت ($$DC$$) عموماً پارامتر راکتانس تعریف نمی‌شود. دلیل این امر را می‌توان در مفهوم راکتانس جست‌وجو کرد. در واقع میدان الکتریکی در خازن و میدان مغناطیسی در سلف، در جریان‌های الکتریکی متناوب ($$AC$$) در برابر تغییر جهت جریان مخالفت می‌کنند. این مخالفت را مقاومت واکنشی یا همان راکتانس می‌نامند.

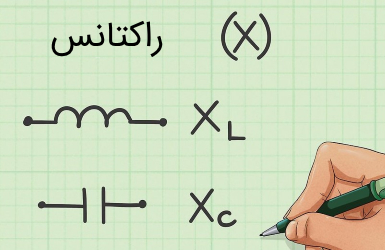
راکتانس خازنی ($$X_{C}$$) ناشی از مخالف بودن جهت میدان الکتریکی بین صفحات خازن با جهت جریان است. خازن در یک جریان الکتریکی متناوب ($$AC$$) به طور مدام با عوض شدن جهت جریان، شارژ و دشارژ می‌شود. در واقع به هنگام شارژ جهت جریان عوض شده و بارهای قبلی که در راستای شارژ شدن در صفحات خازن جمع شده بودند (میدان حاصل از آن‌ها) در برابر دشارژ شدن مقاومت می‌کنند. هر چه سرعت تغییر جهت جریان بیشتر باشد، میزان راکتانس خازنی کاهش می‌یابد، چرا که می‌توان گفت بار کمتری به هنگام شارژ در صفحات ذخیره می‌شود.

در راکتانس سلفی ($$X_{L}$$) نیز میدان مغناطیسی تولید شده مطابق با قانون لنز، با تغییر جهت جریان الکتریکی مخالفت می‌کند.

راکتانس خازن ($$X_{C}$$)

همان‌طور که اشاره کردیم، راکتانس خازنی با افزایش سرعت تغییر جهت جریان یا در واقع همان فرکانس، کاهش می‌یابد. دلیل این امر را می‌توان در رابطه زیر دید:

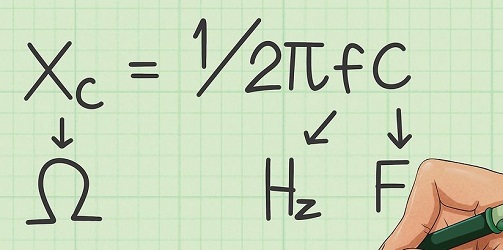
در رابطه فوق، $$f$$ فرکانس با واحد سنجش هرتز ($$Hz$$) و $$C$$ ظرفیت خازن با واحد سنجش فاراد ($$F$$) است. با تعریف فرکانس زاویه‌ای رابطه فوق به صورت زیر در می‌آید:

$$\large \omega=2\pi f \rightarrow X_{C}=\frac{1}{\omega C}$$

راکتانس سلف ($$X_{L}$$)

از رابطه راکتانس سلفی مشخص است که با افزایش سرعت تغییر جهت جریان یا در واقع افزایش فرکانس، مقدار $$X_{L}$$ افزایش پیدا می‌کند. رابطه راکتانس سلفی به صورت زیر است:

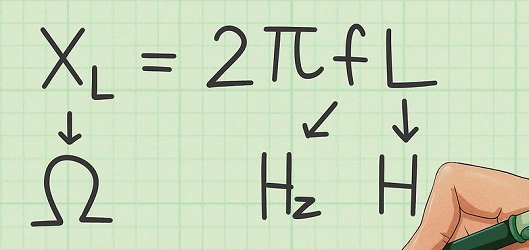
در رابطه فوق، $$f$$ فرکانس با واحد سنجش هرتز ($$Hz$$) و $$L$$ اندوکتانس سلف با واحد سنجش هانری ($$H$$) است. رابطه فوق با تعریف فرکانس زاویه‌ای، به صورت زیر در می‌آید:

$$\large \omega=2\pi f \rightarrow X_{L}=\omega L$$

جهت آشنایی بیشتر با پارامتر اندوکتانس و وابستگی‌های آن به ساختار سلف به مقاله «اندوکتانس سیم پیچ — به زبان ساده» مراجعه کنید.

محاسبه امپدانس کل

جهت محاسبه امپدانس کل یک مدار، باید مقاومت کل (معادل) تمامی عناصر مقاومتی و راکتانس کل (معادل) تمامی عناصر پسیو سلف و خازن را بدانیم.

فیلم آموزش فیزیک عمومی ۲ – حل مساله در فرادرس

کلیک کنید

مقاومت کل

همان‌طور که مطلب «مقاومت موازی — به زبان ساده» و «مقاومت سری — به زبان ساده» دیدیم، محاسبه مقاومت کل (معادل) مقاومت‌هایی که به صورت موازی یا سری در یک مدار الکتریکی بسته شده‌اند، کار ساده‌ای است. توجه داشته باشید که اگر مدار تنها شامل عناصر مقاومت باشد، امپدانس کل برابر با مقاومت معادل مدار است.

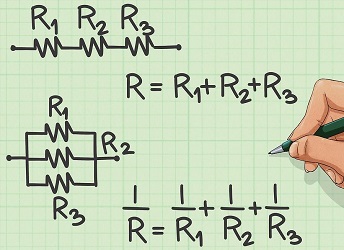
راکتانس کل

از آنجایی که واحد سنجش راکتانس همانند مقاومت معمولی ($$R$$)، اُهم است، محاسبه راکتانس کل مدار همانند روشی است که در بررسی مقاومت‌های موازی و سری پیش گرفتیم. در واقع راکتانس خازنی یا سلفی معادل برای عناصری که به طور سری بسته شده‌اند به صورت $$X_{T}=X_{1}+X_{2}+...$$ و برای حالت موازی، به صورت $$\frac{1}{X_{T}}=\frac{1}{X_{1}}+\frac{1}{X_{2}}+...$$ است. به شکل زیر دقت کنید.

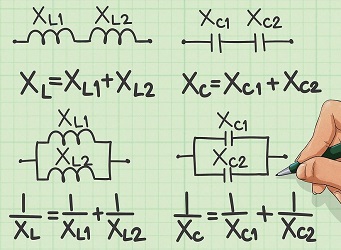
حال اگر دو عنصر سلف و خازن به صورت سری قرار گرفته‌ باشند، راکتانس معادل آن‌ها به صورت زیر محاسبه می‌شود:

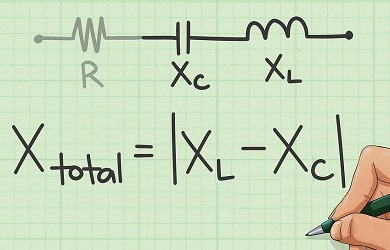
به یاد داشته باشید به دلیل تفاوت فاز در جریان و ولتاژ سلف و خازن در جریان‌های متناوب، نمی‌توان راکتانس‌ها را با یکدیگر جمع کرد. در واقع راکتانس‌های خازنی و سلفی هر کدام در زمان‌های متفاوتی به حداکثر مقدار خود می‌رسند. نمودار فازوری ولتاژ یک مدار RLC سری به صورت زیر است:

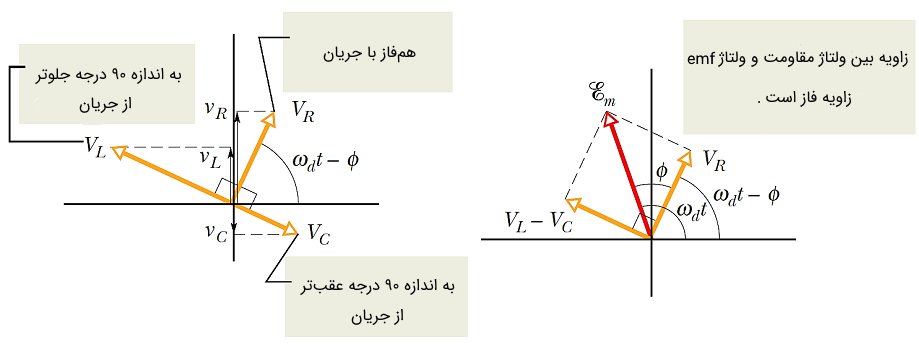
از نمودار فوق پی می‌بریم که اگر دو مقدار $$X_{C}$$ و $$X_{L}$$ با یکدیگر برابر باشند، مقدار راکتانس کل مدار RLC صفر می‌شود. این اتقاق در فرکانسی موسوم به فرکانس تشدید یا «رزونانس» (Resonance) رخ می‌دهد. در این حالت امپدانس مدار تنها ناشی از عنصر مقاومتی $$R$$ است.

جهت محاسبه فرکانس رزونانس از رابطه زیر استفاده می‌کنیم:

$$\large X_{L}=X_{C} \rightarrow \omega L=\frac{1}{\omega C} \Rightarrow \omega_{resonance}=2\pi f_{resonance}=\frac{1}{\sqrt{LC}}$$

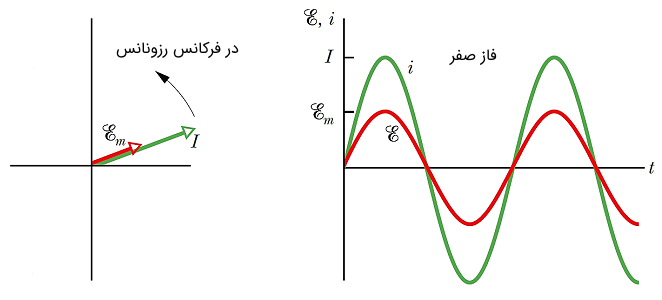
امپدانس مدار RLC سری

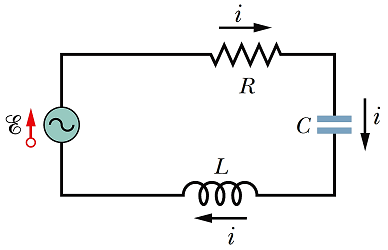
در صورتی که هر سه عنصر پسیو مقاومت، سلف و خازن به صورت سری در یک مدار قرار گرفته باشند (شکل 10)، برای محاسبه راکتانس کل از رابطه $$X=|X_{L}-X_{C}|$$ استفاده می‌کنیم. دقت شود که برای عنصر مقاومت، پارامتر راکتانس تعریف نمی‌شود.

با توجه به مطالب فوق، امپدانس کل یک مدار RLC سری به صورت زیر محاسبه می‌شود.

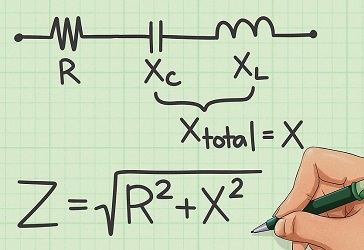
برای مدار RC و RL نیز داریم:

فرمول امپدانس

در کل امپدانس عددی مختلط بوده که در فوق، اندازه آن را محاسبه کردیم. در واقع امپدانس شامل بخش حقیقی مقاومت $$R$$ و بخش موهومی راکتانس $$X$$ به صورت زیر است:

$$\large Z=R+jX \rightarrow Z=R+Z=R+j(X_{L}−X_{C})$$
(1)

از رابطه فوق مشخص است که اگر جریان الکتریکی ثابت باشد، بخش موهومی صفر بوده و امپدانس تنها حاصل از بخش حقیقی مقاومت $$R$$ است. البته شاید جمله صحیح‌تر این باشد که در جریان‌های ثابت، راکتانس تعریف نشده و  امپدانس تنها شامل مقاومت حقیقی $$R$$ است.

از آنجایی که امپدانس نیز از جنس مقاومت است و با واحد اهم سنجیده می‌شود، محاسبه امپدانس معادل در مدارات الکتریکی، همانند مقاومت‌های معمولی موازی و سری است.

$$series \rightarrow Z_{T}=Z_{1}+Z_{2}+...$$
(2)

$$parallel \rightarrow\frac{1}{Z_{T}}=\frac{1}{Z_{1}}+\frac{1}{Z_{2}}+...$$
(3)

برای راحتی محاسبه امپدانس برای حالت موازی (دوری از رابطه کسری)، پارامتر جدیدی موسوم به «ادمیتانس» (Admittance) تعریف می‌کنند. ادمیتانس عکس امپدانس و به صورت زیر تعریف می‌شود:

$$\large Y=\frac{1}{Z}=\frac{1}{R+jX}$$
(4)

در نتیجه از قانون اهم، رابطه بین اختلاف پتانسیل (ولتاژ) $$V$$ و جریان $$I$$ به صورت زیر در می‌آيد:

$$\large V=IZ \Leftrightarrow I=VY$$
(5)

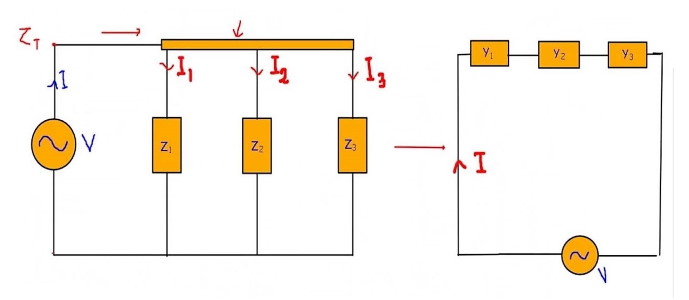
از آنجا که رابطه ادمیتانس $$Y$$ شامل عددی مختلط است، می‌توانیم با ضرب مزدوج مختلط امپدانس $$Z$$ در صورت و مخرج رابطه (۴)، ادمیتانس را به صورت زیر بنویسیم:

$$\large Y=\frac{Z^{*}}{|Z|^{2}}=\frac{R-jX}{R^{2}+X^{2}}$$
(6)

جهت نمایش بهتر، رابطه فوق را می‌توان با جدا کردن مخرج مشترک، به صورت زیر نوشت که در آن $$G$$ «کنداکتانس» (Conductance) و $$B$$ سوسپتانس (Susceptance) است.

$$\large Y=G+jB$$
(7)

 پارامترهای $$Y$$، $$G$$ و $$B$$، با وحد زیمنس (Siemens) یا $$mho$$ با نماد $$Ω^{-1}$$ سنجیده می‌شوند.

^^