پارامترهای خط انتقال در مهندسی قدرت — به زبان ساده

خط انتقال، یکی از اجزای اصلی سیستم قدرت است و میتوان آن را با سه مشخصه یا پارامتر مقاومت، اندوکتانس و ظرفیت نشان داد. در این آموزش از مجله فرادس، پارامترهای خطوط انتقال را بررسی خواهیم کرد.
مقاومت
بزرگترین اثر مقاومت در هادیهای خطوط انتقال، تولید تلفات $$I^2R$$ است. مقاومت، همچنین افت ولتاژ $$IR$$ را تولید میکند که بر تنظیم ولتاژ خط تاثیر میگذارد.
مقاومت dc یک هادی ($$R$$) بهطول $$l$$ و سطح مقطع $$A$$ با رابطه زیر و برحسب اهم بیان میشود:

که در آن، $$\rho$$ مقاومت ویژه هادی برحسب اهم-متر است. مقاومت dc یک هادی از دمای عملکرد تاثیر میپذیرد و رابطه خطی با آن دارد. هرچند، وقتی جریان متناوب از یک هادی بگذرد، توزیع چگالی جریان گذرنده از سطح مقطع هادی، غیریکنواخت بوده و تابعی از فرکانس ac است. این پدیده که بهعنوان «اثر پوستی» (Skin Effect) شناخته شده، سبب میشود مقاومت ac بیشتر از مقاومت dc باشد. در فرکانس 60 هرتز، مقاومت dc یک هادی خط انتقال ممکن است 5 تا 10 برابر بزرگتر از مقاومت dc باشد.
وابستگی مقاومت به دما، با رابطه زیر بیان میشود:
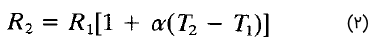
که در آن، $$R_1$$ و $$R_2$$ بهترتیب، مقاومت در دماهای $$t_1$$ و $$t_2$$ هستند. همچنین، $$\alpha$$، ضریب دمای مقاومت نامیده میشود. مقاومت ویژه و ضریب دمای چند نوع فلز، در جدول زیر آورده شده است:
| ماده | مقاومت ویژه $$\rho$$ در دمای $$20^ \circ C$$ (برحسب $$\mu \Omega \cdot cm$$) | ضریب دمای $$\alpha$$ در دمای $$20^ \circ C$$ (برحسب $$^ \circ C^{-1}$$) |
| آلومینیوم | 2.83 | 0.0039 |
| برنج | 6.4-8.4 | 0.0020 |
| مس آنیل شده | 1.77 | 0.00382 |
| مس سخت | 1.72 | 0.00393 |
| آهن | 10.0 | 0.0050 |
| نقره | 1.59 | 0.0038 |
| فولاد | 12-88 | 0.001-0.005 |
در خطوط انتقال طولانی، علاوه بر مقاومت سری، با مقاومتهای شنت (کندوکتانس یا رسانایی) نیز سروکار داریم.
اندوکتانس
اندوکتانس هادی برای دو سیم تکفاز خط انتقال، با رابطه زیر و برحسب هانری بر متر بیان میشود:

که در آن، $$\mu _0=4 \pi \times 10^ {-7} \, H/m$$ (ضریب نفوذ هوا)، $$D$$ فاصله بین مراکز هادیها، و $$r$$ شعاع آنها است. بنابراین، اندوکتانس کل یا حلقه برابر است با
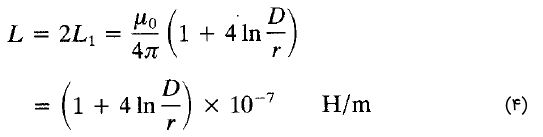
از آنجایی که $$ln \, e^{1/4}=1/4$$، معادله بالا را میتوان بهصورت زیر نوشت:
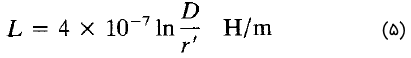
که در آن، $$r'=re^{-1/4}$$ بهعنوان شعاع متوسط هندسی (Geometrical Mean Distance) یا GMR هادی شناخته میشود.
از دو جمله رابطه (3)، اولی اندوکتانس داخلی هادی، و جمله دوم، ناشی از شار خارجی هادی است. در معادله (۵)، هادی با یک پوسته نازک توخالی رسانا با شعاع $$r'$$ جایگزین میشود که شار پیوندی درونی و در نتیجه، اندوکتانس داخلی ندارد.
خط سهفاز سهسیمه
اندوکتانس هر فاز (یا خط به خنثی) یک خط انتقال سهفاز که فاصله هادیها در آن برابر است، با رابطه زیر داده میشود:
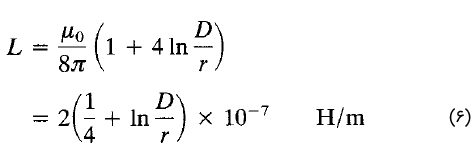
که در آن، $$r$$ شعاع هادی و $$D$$ فاصله بین هادیها است. در عمل، سه هادی خط سهفاز، بهندرت فاصله متوازنی دارند. این فاصله نامتقارن، سبب تولید اندوکتانسهای نابرابر و در نتیجه افت ولتاژهای متفاوت در سهفاز و عدم تعادل خط میشود. برای متعادل کردن این عدم تعادل، موقعیت هادیها در بازههای مشخصی در طول خط تغییر میکند. این کار را «ترانهش» یا جابهجایی (Transposition) مینامند که در شکل ۱ نشان داده شده است. در این شکل، فاصلههای نابربر بین هادیها نیز مشخص شده است.
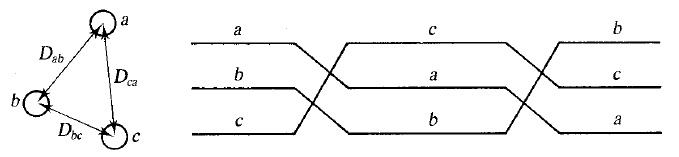
اندوکتانس میانگین هر فاز یک خط جابهجاشده را میتوان با رابطه (۶) محاسبه کرد، البته در این رابطه باید فاصله $$D$$ را با فاصله میانگین $$D_e$$ تعویض کرد که از رابطه زیر بهدست میآید:
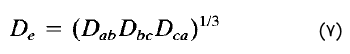
که فاصلههای $$D_{ab}$$، $$D_{bc}$$ و $$D_{ca}$$ در شکل 1 مشخص شدهاند.
هادیهای مرکب
عباراتی که برای توصیف اندوکتانس خط بیان شد، باید اصلاح شوند تا بتوان آنها را به یک خط انتقال شامل هادیهای مرکب اعمال کرد. بهطور خاص، فرض کنید یک خط تکفاز مطابق شکل ۲ از دو هادی مرکب تشکیل شده باشد. هادی X از $$n$$ رشته مشابه و موازی تشکیل شده که از هر کدام جریان $$I/n$$ میگذرد. هادی Y نیز که مدار برگشت جریان هادی X است، از $$m$$ رشته مشابه و موازی تشکیل شده که جریان هرکدام از آنها $$-I/m$$ است. فاصله بین هر دو عنصر با $$D$$ نشان داده میشود که اندیس مناسب نیز میگیرد. اندوکتانس $$L_x$$ هادی X با رابطه زیر و برحسب هانری بر متر بیان میشود:
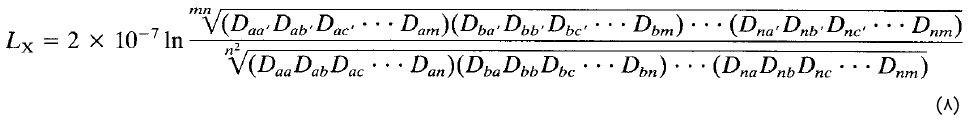
که در آن، $$D_{kk}=r'_k=r_ke^{-1/4}$$ شعاع متوسط هندسی (GMR) مربوط به $$k$$اُمین هادی است. توجه کنید که صورت کسر رابطه (۸)، ریشه $$mn$$اُم ضرب $$mn$$ جمله است. هر کدام از این جملات، فاصله یکی از $$n$$ رشته هادی X از یکی از $$m$$ رشته هادی Y است. بنابراین، $$mn$$ فاصله وجود دارد. ریشه $$mn$$اُم ضرب $$mn$$ فاصله، فاصله میانگین هندسی (Geometric mean distance) نامیده میشود. برای دو هادی X و Y شکل 2، فاصله میانگین هندسی متقابل (Mutual) تعریف میشود که بهاختصار آن را $$D_m$$ یا GMD مینامند.
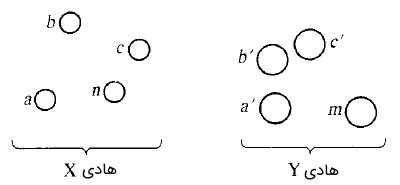
در مخرج کسر رابطه (۸)، ریشه $$n^2$$ ضرب $$n^2$$ فاصله گرفته میشود که آن را با $$D_s$$ نشان میدهیم و GMD خودی هادی X مینامیم. به طریق مشابه، $$r'$$ یک رشته یا سیم مجزا، اغلب GMD خودی نامیده میشود. اصطلاح GMD خودی، شعاع میانگین هندسی (Geometric mean radius) یا بهاختصار GMR نام دارد.
معادله (۸) را میتوان بهصورت زیر نوشت:
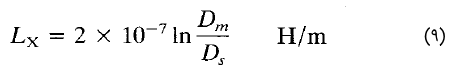
اندوکتانس $$L_Y$$ بهطریق مشاهب بهدست میآید و اندوکتانس کل خط برابر است با:
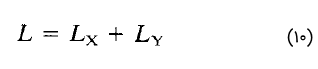
خط سهفاز دومداره
اندوکتانس هر فاز یک خط انتقال جابهجاشده سهفاز دومداره (شکل ۳)، با رابطه زیر داده میشود:
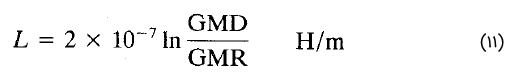
مطابق نمادهای شکل ۳، معادله (۱۱) را میتوان بهصورت زیر نوشت:
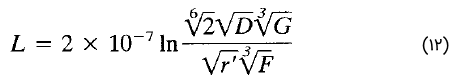
که در آن، $$r'$$ نشاندهنده GMR هادی است.
ظرفیت
ظرفیت شنت یا موازی بر واحد طول برای یک خط انتقال تکفاز دوسیمه با رابطه زیر و برحسب فاراد بر متر بیان میشود:
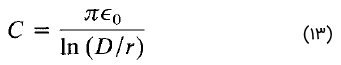
که در آن، $$\epsilon _0$$ نفوذپذیری الکتریکی هوا است. ظرفیت هر فاز (خط به خنثی) یک خط سهفاز با هادیهای منظم بهصورت زیر است:
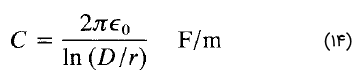
همانطور که گفتیم، در عمل فاصله بین هادیها یکسان نیست، بنابراین میتوان $$D$$ را با $$D_e$$ که در رابطه (۷) بیان شد، جایگزین کرد.
ظرفیت هر فاز خط انتقال دومداره شکل ۳ بهصورت زیر بیان میشود:
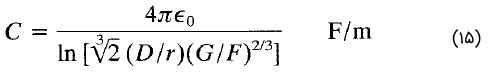
ظرفیت یک خط انتقال هوایی تحت تاثیر زمین قرار میگیرد. برای بررسی اثر زمین، تصویر آینهای هادیها را پایینتر از سطح زمین و به اندازه فاصله آنها تا سطح زمین درنظر میگیریم (شکل 4). همانگونه که در شکل ۴ نشان داده شده است، بار الکتریکی تصویر هادیها مخالف هادیهای هوایی است. بنابراین، ظرفیت نسبت به خنثی برابر است با:

که در آن، $$D_e$$ از رابطه (۷) بهدست میآید و $$H$$ در شکل ۴ تعریف شده است. $$r$$ نیز شعاع هادی است.
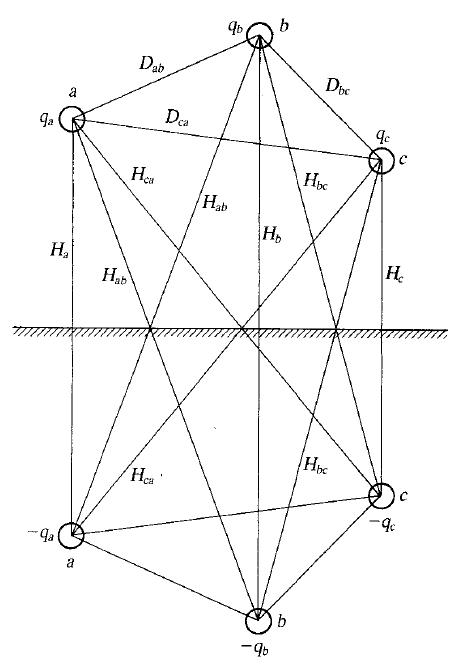
با استفاده از مفهوم GMD میتوان ظرفیت را نسبت به خنثی برای یک خط دومداره سهفاز نامتقارن بهصورت زیر نوشت:
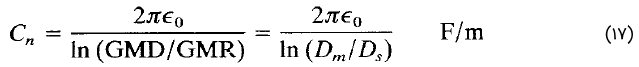
با جایگذاری مقدار عددی $$\epsilon _0$$ در رابطه (۱۷)، داریم:
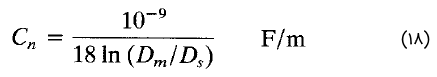
اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای مهندسی قدرت
- مجموعه آموزشهای مهندسی برق
- مجموعه آموزشهای دروس مهندسی برق
- آموزش بررسی سیستم های قدرت 1
- آموزش شبیه سازی سیستم های قدرت با PowerWorld Simulator
- آموزش نرم افزار DIgSILENT برای آنالیز و شبیه سازی سیستم های قدرت
- سیستم پریونیت (Per-Unit) — از صفر تا صد
- نمودار تک خطی (Single Line Diagram) — به زبان ساده
^^











سلام خسته نباشید یه سوال داشتم هرچقد گشتمنتونستم پیداش کنم
زمین چه تاثیری روی اندوکتانس خط دارد
باسلام وخسته نباشید بنده یه سوال خدمت شمادارم وهرچی سرچ میکنم جوابی پیدانمیکنم
شرط تعادل و توازن توان در مدار(سیستم) کدام است تشریح نمایید؟
سلام.
مفهوم بار متعادل در یک سیستم سهفاز این است که توان هر سه فاز با هم برابر باشد.
موفق باشید.
سلام و درود منظور از diagonal resistance چیست ؟
سلام.
فرض کنید یک شبکه مقاومتی به شکل مربع دارید که روی هر ضلع آن یک مقاومت قرار دارد. اگر مقاومتی در مدار قرار دهیم که یک سر آن به یک رأس و سر دیگرش به رأس مقابل متصل باشد، به آن مقاومت، مقاومت قطری میگوییم.
سپاس از همراهیتان با مجله فرادرس.
سلام در مورد سیم های هوایی . مثلا میگن سیم ۱۲۶ یا سیم هفتاد . واحدش میلی متر مربع هست یا میلی متر و چطوری محاسبه میشه؟
ممنون
سلام.
منظور از اعداد مذکور سطح مقطع هادی برحسب میلیمتر مربع است و شرکت سازنده آن را در جدول مشخصات فنی کابل ارائه میکند.
از همراهی شما با مجله فرادرس خوشحالیم.