نمودار تک خطی (Single Line Diagram) — به زبان ساده
نمودار تک خطی، یکی از راههای نشان دادن سیستمهای سهفاز است که در مطالعات پخش بار کاربرد فراوانی دارد. برای سادگی محاسبات مربوط به سیستمهای قدرت، مقادیر مربوط به اجزای سیستم را معمولاً با «پریونیت» (per-unit) نشان میدهند.
در این آموزش، نحوه محاسبه و رسم نمودار تک خطی و مقادیر پریونیت یک سیستم قدرت سه فاز را در قالب دو مثال ساده بیان میکنیم.
مثال اول
فرض کنید یک سیستم قدرت از اجزای زیر تشکیل شده است:
- دو ژنراتور با ولتاژ 13.2Kv
- دو ترانسفورماتور افزاینده 13.2/66Kv که ولتاژ ژنراتورها را افزایش میدهند.
- یک شین (باس) 66Kv در ابتدای خط انتقال
- یک خط انتقال 66Kv
- یک شین 66Kv در انتهای خط انتقال
- یک خط انتقال 66kV با شین وسط
- یک ترانسفورماتور کاهنده 66/12kV که چهار موتور 12kV موازی را تغذیه میکند.
- یک ترانسفورماتور کاهنده 66/7.2kV که یک موتور 7.2kV را تغذیه میکند.
می خواهیم دیاگرام تک خطی سیستم را رسم کنیم. برای این منظور، دو کار ساده زیر را انجام میدهیم:
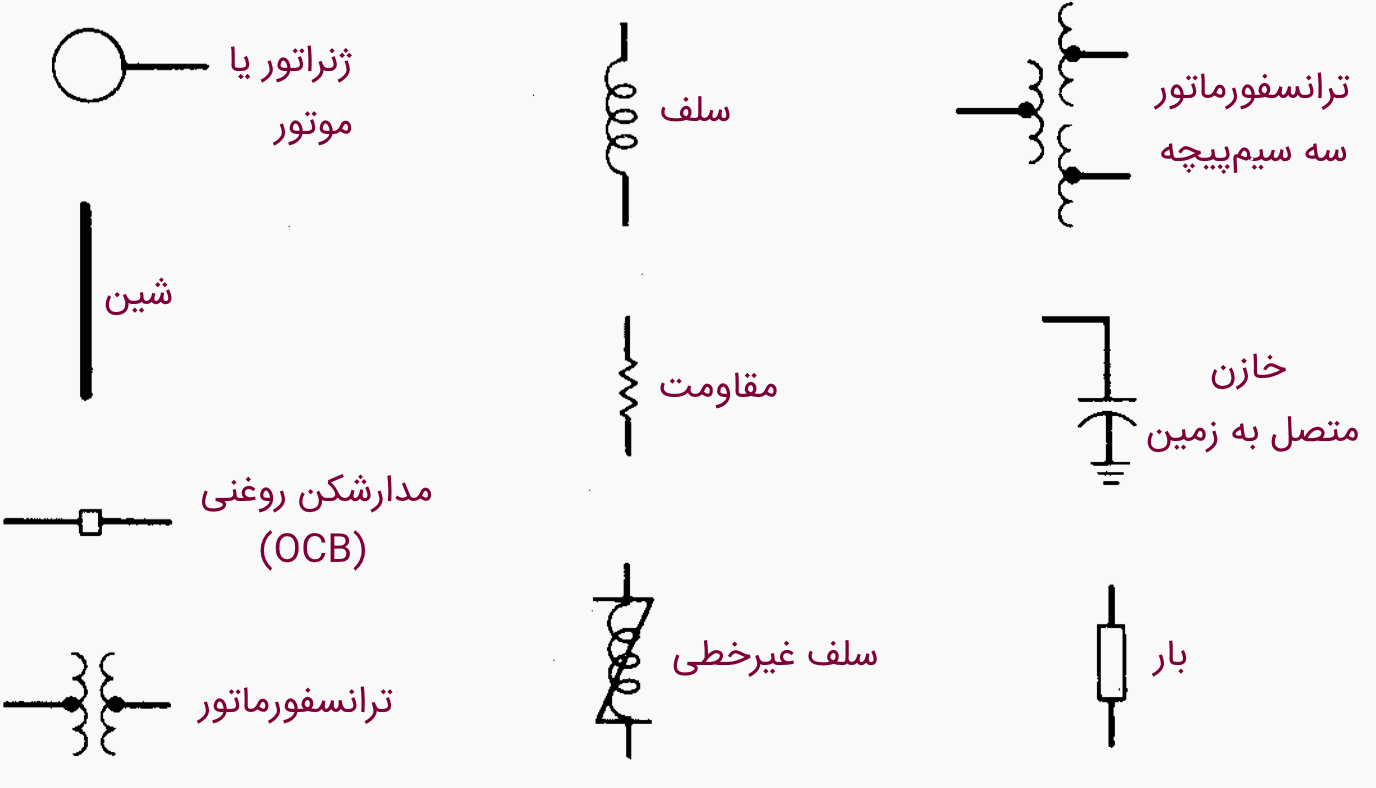
1. انتخاب نمادهای مناسب
در شبکههای قدرت الکتریکی، معمولاً از نمادهای زیر برای نمایش نمودار تک خطی استفاده میشود:
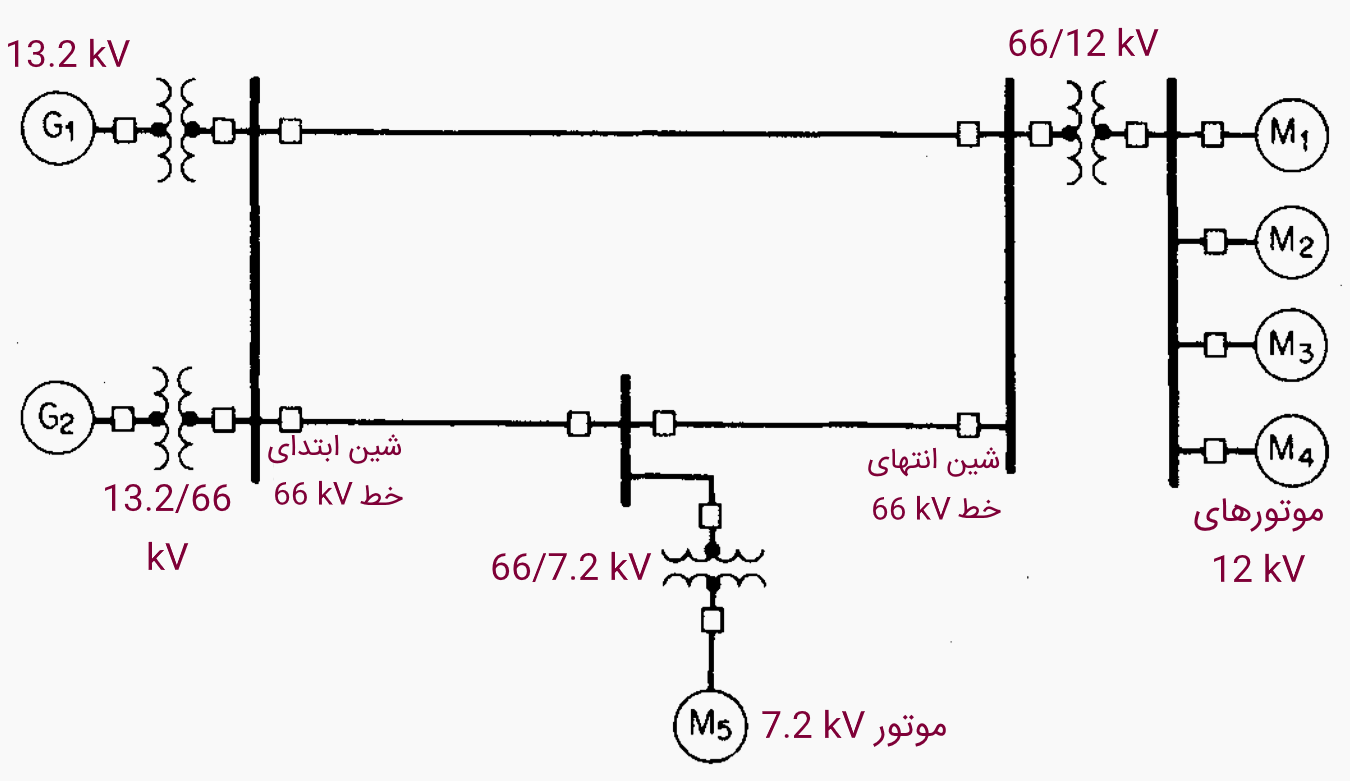
2. رسم نمودار سیستم
شکل 2 سیستم توصیف شده با پارامترهای بالا را نشان میدهد. مدارشکنهای روغنی نیز در نمودار گنجانده شده که برای ایزولاسیون اجزای شبکه است.
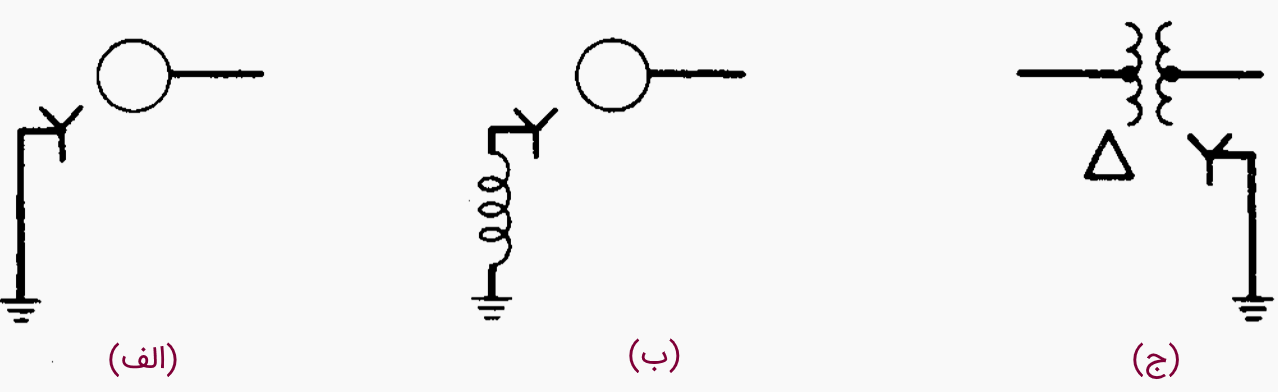
در استفاده از نمودارهای تک خطی برای نمایش سیستمهای سه فاز، وقتی با تجهیزات متقارن سروکار داریم، میتوانیم نمودارهای متفاوتی را برای این اجزا رسم کنیم. علاوه بر این، اغلب لازم است اتصال زمین را (چه برای اتصال ستاره و چه مثلث) مشخص کنیم. شکل 3، انواع اتصال به زمین تجهیزات سه فاز را نشان میدهد.
مثال 2
مشخصات سیستم قدرت شکل 4 در جدول زیر آورده شده است. مدار معادل الکتریکی یا نمودار راکتانس سیستم را برحسب مقادیر پریونیت به دست آورید. فرض کنید هر دو موتور در ولتاژ 12kV، سه چهارم بار کامل و ضریب توان واحد کار میکنند.
| ژنراتور | ترانسفورماتورها | موتور A | موتور B | خط انتقال |
| 13.8kV | 25,000kVA | 15,000kVA | 10,000kVA | - |
| 25,000kVA 3-phase | 13.2/69kV | 13kV | 13kV | - |
| X"=15% | $$X_L=15\%$$ | X"=15% | X"=15% | $$X=65 \Omega$$ |
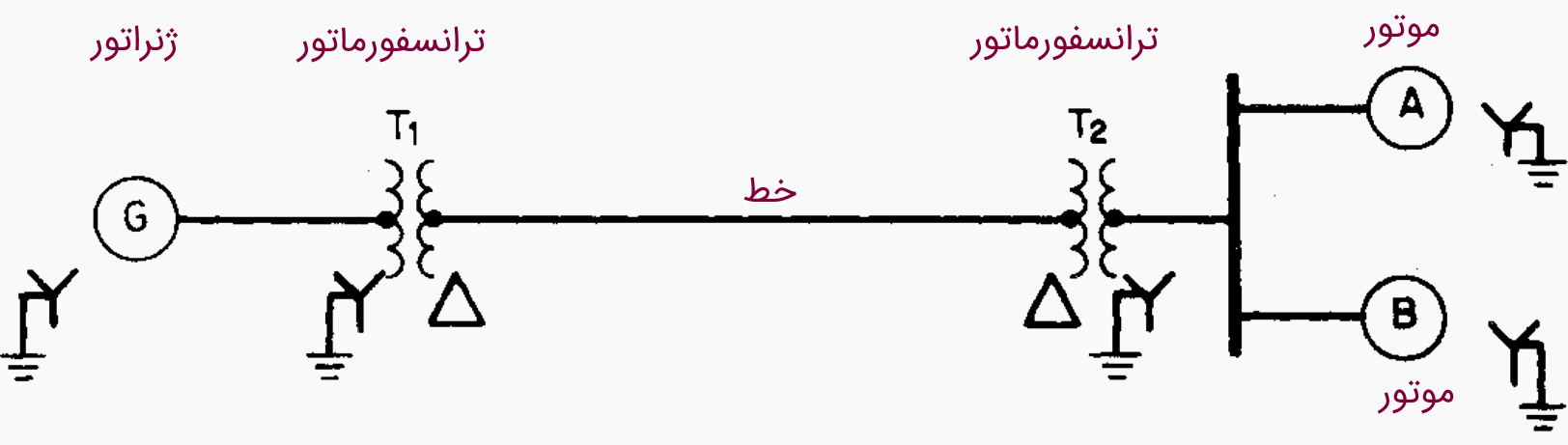
محاسبات را در 8 گام انجام میدهیم:
1. تعیین ولتاژ پایه سیستم
با مشاهده اندازه اجزای سیستم، یک مقدار پایه توان ظاهری S را انتخاب میکنیم. این مقدار اختیاری است. در این مثال، مقدار 25,000kVA را به عنوان توان ظاهری پایه انتخاب میکنیم و همزمان، ولتاژ 13.8kV ژنراتور را به عنوان ولتاژ پایه در نظر میگیریم.
ولتاژ پایه خط انتقال را میتوان با داشتن نسبت ولتاژ محاسبه کرد:
$$(13.8kV)(69kV/13.2kV)=72.136kV$$
ولتاژ پایه موتورها نیز به طریق مشابه با استفاده از ولتاژ 72.136kV محاسبه میشود:
$$(72.136kV)(13.2kV/69kV)=13.8kV$$
مقدار توان پایه S در سراسر سیستم ثابت باقی میماند، اما ولتاژ پایه ژنراتور و موتورها، 13.8kV و ولتاژ پایه خط انتقال 72.136kV است.
2. محاسبه راکتانس ژنراتور
از آنجایی که مقدار راکتانس ژنراتور برحسب پریونیت (با مقادیر پایه 25,000kVA و 13.8kvA که برابر با مقادیر پلاک است) داده شده، نیازی به محاسبه آن نداریم.
3. محاسبه راکتانس ترانسفورماتور
چون مقادیر ولتاژ و توان پایه راکتانس داده شده ترانسفورماتور با مقادیر پایه انتخاب شده ما یکسان نیست، باید مقدار پریونت راکتانس آن را تصحیح کنیم:
$$^2$$(kV پایه/kV پلاک)(kVA پلاک/kVA پایه)(راکتانس پریونیت پلاک)=راکتانس جدید
$$(0.11)(25,000/25,000)(13.2/13.8)^2=0.101p.u.$$=
4. محاسبه راکتانس خط انتقال
$$^2$$(kV پایه)(1000)/(kVA پایه)(راکتانس اهمی)=$$X_{pu}$$
$$x_{pu}=(65)(25,000)/(1000)(72.1)^2=0.313pu$$
5. محاسبه راکتانس موتورها
در اینجا لازم است مقادیر راکتانس پلاک موتورها را تصحیح کنیم، زیرا مقادیر kVA و kV نامی موتورها نسبت به مقادیری که ما انتخاب کردهایم تفاوت دارد. بنابراین، از رابطه تصحیحکننده مرحله 3 برای محاسبه مقادیر جدید استفاده میکنیم:
$$X"_A=(0.15\, p.u.)(25,000\, kVA/15,000 \, kVA)(13\, kV/13.8\, kV)^2=0.222\, p.u.$$
$$X"_B=(0.15\, p.u.)(25,000\, kVA/10,000 \, kVA)(13\, kV/13.8\, kV)^2=0.333\, p.u.$$
6. رسم نمودار راکتانس
مدار معادل راکتانس سیستم به صورت زیر است:
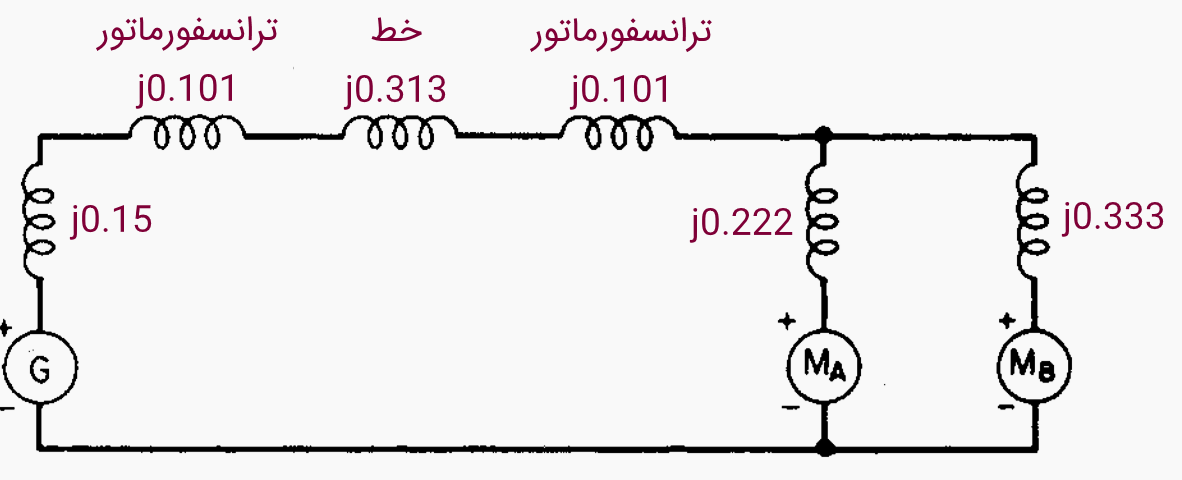
۷. محاسبه شرایط کاری موتورها
اگر موتورها در ولتاژ 12kV کار کنند، مقدار ولتاژ پریونیت آنها $$12kV/13.8kV=0.87pu$$ خواهد بود. در ضریب توان واحد، بار سه چهارم یا 0.75 پریونیت داده شده است.
بنابراین، جریان موتور با استفاده از رابطه زیر به دست میآید:
$$ puI_{pu}=P_{pu}/V_{pu}=0.75/0.87=0.862 \angle 0^\circ$$
۸. محاسبه ولتاژ ترمینال ژنراتور
ولتاژ ترمینال ژنراتور با رابطه زیر محاسبه میشود:
افت ولتاژ ترانسفورماتورها و خط انتقال$$V_G=V_{motor}+$$
$$V_G=0.87\angle 0^\circ+0.862\angle 0^\circ (j0.101+j0.313+j0.101)$$
$$V_G=0.87+j0.444=0.977\angle 27.03^\circ pu$$
برای به دست آوردن ولتاژ واقعی، مقدار ولتاژ پریونیت را در مقدار ولتاژ پایه ژنراتور ضرب میکنیم. بنابراین داریم:
$$V_G=(0.977\angle 27.03^\circ)(13.8 kV)=13.48\angle 27.03^\circ kV$$
انتخاب توان ظاهری و ولتاژ پایه اختیاری است. ولتاژ پایه هر بخش از سیستم را نیز میتوان طبق نسبت ولتاژ ترانسفورماتور در نظر گرفت.
پایه امپدانس با رابطه زیر محاسبه میشود:
$$Z_{base \,}=(V_{base})^2(1000)/(S_{base})$$
که $$V_{base}$$ برحسب kV و $$S_{base}$$ برحسب kVA است.
در مثالی که بیان شد، راکتانس پایه خط انتقال $$Z_{base}=(72.136)^2(1000)/(25,000)=208.1$$ است. بنابراین، راکتانس پریونیت برابر $$65/208.1=0.313$$ خواهد بود.
^^










