قوانین KVL و KCL – به زبان ساده

گاهی، استفاده از قانون اهم برای به دست آوردن ولتاژ و جریان مدارهای پیچیده، دشوار است. در نتیجه، برای انجام محاسبات مربوط به این مدارها به قوانینی نیاز داریم که بتوانیم بر اساس آن، معادلات مدار را به دست آوریم. قانون مداری کیرشهف، یکی از راه‌حل‌های مناسب برای این کار است.

در سال 1875، فیزیکدان آلمانی، «گوستاو کیرشهف»، دو قانون بیان کرد که مربوط به جریان و انرژی در مدارهای الکتریکی بود؛ «قانون جریان کیرشهف» (Kirchhoffs Current Law) یا KCL که مربوط به جریان در یک مدار بسته است و «قانون ولتاژ کیرشهف» (Kirchhoffs Voltage Law) یا KVL که به ولتاژهای یک مدار بسته می‌پردازد.

قانون اول کیرشهف؛ قانون جریان (KCL)

قانون جریان کیرشهف یا KCL بیان می‌کند: «جریان یا بار الکتریکی وارد شده به یک گره دقیقاً برابر با بار یا جریانی است که از آن خارج می‌شود». به عبارت دیگر، مجموع جبری تمام جریان‌های وارد شده به یک گره باید برابر صفر باشد ($$I_{(exiting)}+I_{(entering)}=0$$).

این ایده کیرشهف، با نام پایستگی یا بقای بار نیز شناخته می‌شود.

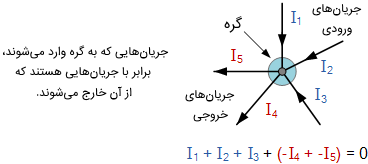
در شکل بالا، مقدار سه جریان $$I_1$$، $$I_2$$ و $$I_3$$ که به گره وارد می‌شوند، مثبت است و دو جریان $$I_4$$ و $$I_5$$ که از گره خارج می‌شوند، منفی هستند. معادله زیر، رابطه بین جریان‌ها را بیان می‌کند:

$$I_1+I_2+I_3-I_4-I_5=0$$

اصطلاح گره در مدارهای الکتریکی معمولاً به اتصال یا پیوند دو یا بیشتر از دو مسیر حامل جریان مانند سیم یا قطعات الکتریکی اتلاق می‌شود. برای جریانی که به گره وارد یا از آن خارج می‌شود، باید یک مسیر بسته وجود داشته باشد. وقتی با تحلیل مدارهای موازی سر و کار داریم، می‌توانیم از KCL استفاده کنیم. آشنایی با مدارهای الکتریکی و چگونگی حل مسائل مرتبط با آن‌ها برای درک دروس پیشرفته مهندسی برق بسیار مهم هستند. با مراجعه به مجموعه آموزش مدارهای الکتریکی درس، تمرین، حل مثال و تست فرادرس به راحتی می‌توانید مدارهای الکتریکی را از پایه یاد بگیرید.

قانون دوم کیرشهف؛ قانون ولتاژ (KVL)

قانون ولتاژ کیرشهف یا KVL بیان می‌کند: «در هر شبکه حلقه بسته، کل ولتاژ حلقه برابر با مجموع تمام افت ولتاژهای موجود در آن است».

فیلم آموزش مبانی مهندسی برق ۱ – مرور و حل مساله در فرادرس

کلیک کنید

به عبارت دیگر، مجموع تمام ولتاژهای حلقه باید برابر با صفر باشد. این ایده کیرشهف، به عنوان بقا یا پایستگی انرژی نیز شناخته می‌شود.

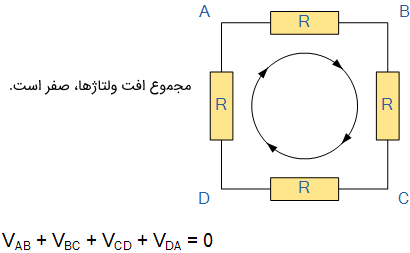
برای نوشتن معادله بر ولتاژ حلقه، باید از یک نقطه آن شروع کنیم، در یک جهت یکسان همه افت ولتاژها را بنویسیم و به همان نقطه اول باز گردیم. این نکته مهم است که وقتی افت ولتاژها را می‌نویسیم تغییر جهت ندهیم، زیرا با تغییر جهت، دیگر مجموع ولتاژها صفر نخواهد بود. از قانون ولتاژ کیرشهف می‌توان در مدارهای سری استفاده کرد.

وقتی یک مدار DC یا AC را با استفاده از قوانین مداری کیرشهف تحلیل می‌کنیم، با واژه‌ها و اصطلاحاتی روبرو می‌شویم که بخش‌های مختلف مدار را توصیف می کنند، مانند گره، مسیر، شاخه، حلقه و مش. این اصطلاحات در مدارهای الکتریکی بسیار تکرار می‌شوند و دانستن آن‌ها امری ضروری است.

اصطلاحات مدارهای DC

• مدار (Circuit): یک مدار، مسیر هادی حلقه بسته‌ای است که  جریان الکتریکی در آن برقرار می‌شود.
• مسیر (Path): یک خط از عناصر یا منابع متصل به هم است.
• گره (Node): گره، یک اتصال یا پیوند از مدار است که در آن، دو یا بیشتر از دو عنصر مدار به هم متصل هستند. گره را با یک نقطه مشخص می‌کنیم.
• شاخه (Branch): شاخه، یک یا گروهی از اجزای مدار مانند مقاومت یا منبع است که بین دو گره وصل شده‌اند.
• حلقه (Loop): حلقه، یک مسیر بسته در مدار است که اگر از یک نقطه شروع کنیم و به همان جا برگردیم، بیش از یک بار از هر عنصر عبور نکرده باشیم.
• مش (Mesh): مش، ساده‌ترین حلقه مدار است که شاخه‌ای در آن نیست.

شکل زیر گره، حلقه و شاخه را در یک مدار ساده نشان می‌دهد.

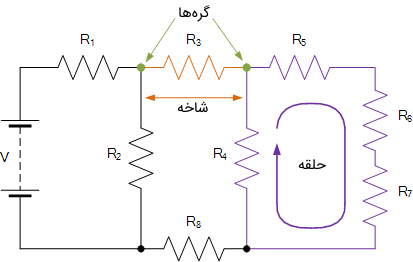
دقت کنید که می‌گوییم اجزیای مدار به صورت سری به هم متصل هستند، اگر جریان یکسانی از آن‌ها بگذرد و می‌گوییم موازی هستند، اگر ولتاژ دو سر آن‌ها برابر باشد.

مثال

در مدار شکل زیر، جریان گذرنده از مقاومت $$R_3$$‌ را به دست آورید.

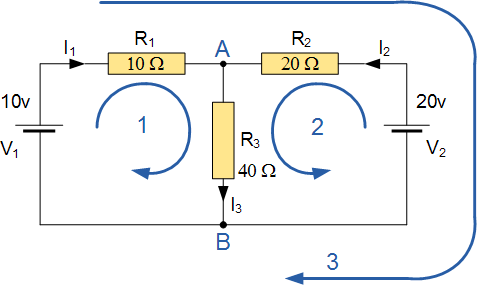
مدار 3 شاخه، 2 گره (A و B) و 2 حلقه مستقل دارد. با استفاده از قانون جریان کیرشهف، معادلات زیر را داریم:

• در گره A: $$I_1+I_2=I_3$$
• در گره B: $$I_3=I_1+I_2$$

قانون ولتاژ کیرشهف نیز منجر به معادلات زیر می‌شود:

• حلقه 1: $$10=R_1I_1+R_3I_3=10I_1+40I_3$$
• حلقه 2: $$20=R_2I_2+R_3I_3=20I_2+40I_3$$
• حلقه 3: $$10-20=10I_1-20I_2$$

از آنجایی که $$I_3$$ برابر با مجموع $$I_1+I_2$$ است، معادلات فوق را می‌توان به صورت زیر بازنویسی کرد:

• معادله اول: $$10=10I_1+40(I_1+I_2)=50I_1+40I_2$$
• معادله دوم: $$20=20I_2+40(I_1+I_2)=40I_1+60I_2$$

اکنون دو معادله داریم که می‌توانیم با استفاده از آن‌ها $$I_1$$ و $$I_2$$ را به دست آوریم. اگر محاسبات لازم را انجام دهیم، مقدار $$I_1=-0.143$$ و $$I_2=+0.429$$‌ آمپر به دست می‌آیند و از آن‌جایی که $$I_3=I_1+I_2$$، مقدار $$I_3=0.286A$$ است. ولتاژ دو سر مقاومت $$R_3$$ نیز برابر است با: $$0.286 \times 40=11.44 V$$.

علامت منفی جریان $$I_1$$‌ به این معنی است که جهت اولیه جریان برای این حلقه اشتباه انتخاب شده بود. در حقیقت، باتری 20 ولتی، باتری 10 ولتی را شارژ می‌کند.

کاربرد قوانین مداری کیرشهف

با کمک دو قانون مداری کیرشهف می‌توان مقادیر ولتاژ و جریان مدار را پیدا کرد. روند اصلی استفاده از این قوانین به صورت زیر است:

1. فرض کنید همه ولتاژها و مقاومت‌ها داده شده‌اند (اگر داده نشده باشند، آن‌ها را نامگذاری کنید، مثلاً V۲ ،V۱ و ... و R۲ ،R۱ و ...).
2. هر شاخه مدار را به عنوان شاخه جریان در نظر بگیرید و نامگذاری کنید ($$I_1$$، $$I_2$$، $$I_3$$ و غیره).
3. معادلات قانون اول کیرشهف را برای هر گره بنویسید.
4. معادلات قانون دوم کیرشهف را برای حلقه‌های مستقل مدار بنویسید.
5. از معادلات خطی به دست آمده استفاده کرده و جریان‌های نامعلوم را بیابید.

مشابه آنچه در مثال بالا انجام دادیم، می‌توانیم از تحلیل حلقه برای محاسبه جریان‌های هر حلقه مستقل استفاده کنیم که محاسبات ریاضی را با کمک قوانین کیرشهف کاهش می‌دهد. در آموزش بعدی، تحلیل جریان مش را معرفی می‌کنیم.

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، پیشنهاد می‌کنیم به آموزش های زیر مراجعه کنید:

• مدارهای جریان مستقیم (DC) — به زبان ساده
• تقویت کننده های الکترونیکی — مجموعه مقالات جامع وبلاگ فرادرس

^^