پخش بار در سیستم قدرت — مفاهیم و معادلات

در آموزشها پیشین مجله فرادرس درباره بررسی سیستمهای قدرت، مباحثی مانند نمودار تکخطی، سیستم پریونیت و پارامترهای خط انتقال را معرفی کردیم. در این آموزش، مفهوم پخش بار و روابط مربوط به آن توضیح خواهیم داد.
تحلیل پخش بار AC، اساساً یک تحلیل حالت ماندگار در شبکه انتقال و توزیع AC است. در پخش بار AC، مقادیر حالت ماندگار ولتاژ شینها، توان دریافتی بارها و نیز تولید توان در هریک از شینهای سیستم، محاسبه میشود. ما در این آموزش، درباره پخش بار سیستم انتقال بحث خواهیم کرد. لازم به ذکر است که سیستم مورد مطالعه، متعادل است که در آن، بارها و خطوط انتقال متعادل هستند (امپدانس هر سه فاز برابر است) و ژنراتورها ولتاژ سهفاز متعادل تولید میکنند (دامنه ولتاژ سهفاز، برابر و اختلاف فاز آنها 120 درجه است).
مدلسازی اجزای سیستم قدرت
اصولاً شبکه انتقال AC از ژنراتورهای سنکرون، بارها، ترانسفورماتورها و خطوط انتقال تشکیل میشود. در محاسبات پخش بار، ژنراتورهای سنکرون را بهصورت صریح نمایش نمیدهیم و مدلسازی آنها بهصورت ضمنی است. در ادامه، این موضوع را توضیح خواهیم داد. اکنون، نحوه مدلسازی اجزای دیگر را بررسی میکنیم.
بارها
همانطور که میدانیم، بارها را میتوان به سه دسته بارهای با توان ثابت، بارهای با امپدانس ثابت و بارهای با جریان ثابت تقسیمبندی کرد. البته در شرایطی که ولتاژ در بازه عملکرد عادی قرار دارد، اغلب بارها توان ثابتی دارند. از آنجایی که هدف از تحلیل پخش بار AC، محاسبه مقادیر حالت ماندگار ولتاژ شینها است، بارها با توان ثابت در نظر گرفته میشوند. در اینجا باید نکته مهمی را یادآور شد؛ از آنجایی که بارها همواره با زمان تغییر میکنند (مصارف همیشه در حال روشن و خاموش شدن هستند)، هر مقدار مشخص بار (MW و یا MVAR) تنها در یک لحظه خاص، معتبر است. بنابراین، همواره تحلیل پخش بار AC برای بارها و ژنراتورها در یک لحظه معین انجام میشود.
خط انتقال
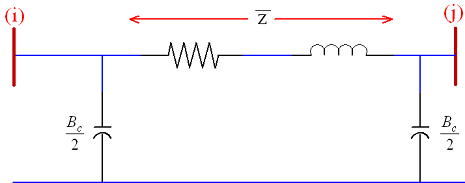
در یک شبکه انتقال، طول خطوط انتقال عموماً بلند یا متوسط است. خط انتقال متوسط را هممیشه با مدل $$\pi$$ نشان میدهیم (شکل ۱) که در آن، $$\bar{z}$$ امپدانس سری کل خط و $$B_c$$ سوسپتانس شارژکننده شنت یا موازی خط است. از سوی دیگر، یک خط انتقال بلند را میتوان بهصورت دقیق با مدار معادل $$\pi$$ نشان داد. این مدل در شکل 2 نشان داده شده است.
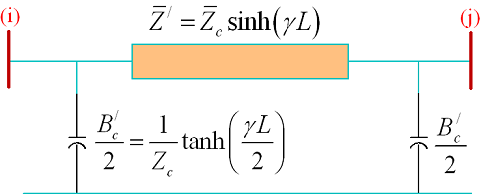
در خطوط انتقال، پارامترهای زیر را داریم:
- $$\bar{Z_c}=\frac{\bar{c}}{\bar{y}}$$: امپدانس مشخصه خط
- $$\gamma=\sqrt{\bar{z}\bar{y}}$$: ضریب انتشار
- $$\bar{z}$$: امپدانس سری طول خط (پریونیت)
- $$\bar{y}$$: ادمیتانس موازی طول خط (پریونیت)
- $$L$$: طول خط
- بنابراین، در تحلیل پخش بار، خط انتقال (متوسط یا بلند) را با مدار معادل $$\pi$$ نشان میدهیم.
ترانسفورماتور
در مطالعات خطا و حالت ماندگار سیستم قدرت، عموماً از جریان تحریک ترانسفورماتور چشمپوشی میشود، زیرا در مقایسه با جریان بار عادی ترانسفورماتور بسیار کوچک است. بنابراین، یک ترانسفورماتور دوسیمپیچه را که بین دو شین $$i$$ و $$j$$ متصل شده، مطابق شکل 3 با امپدانس نشتی پریونیت نشان میدهیم.
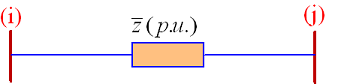
لازم به ذکر است که نسبت دور ترانسفورماتور $$1:1$$ است. مدار معادل یک ترانسفورماتور تنظیم با نسبت دور $$1:t$$ در شکل 4 نشان داده شده است.
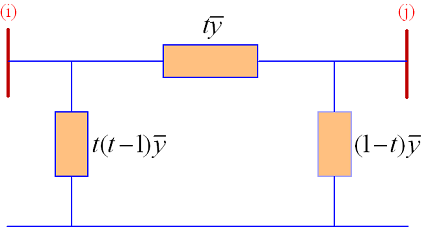
گاهی نسبت دور ترانسفورماتور را با $$a:1$$ نشان میدهند. در این حالت، مدار معادل مطابق شکل ۵ است.
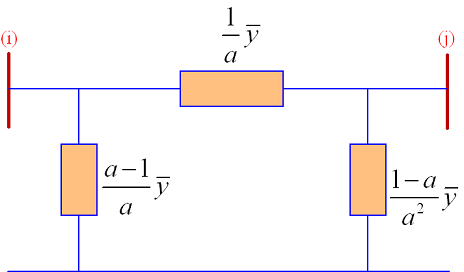
پارامترهای $$t$$ و $$a$$ در شکلهای ۴ و ۵، اعدادی حقیقی هستند (یعنی فقط مقدار دامنه ولتاژ را تغییر میدهند و تأثیری روی فاز ندارند). همچنین در این دو شکل، $$\bar{y}$$ ادمیتانس پریونیت ترانسفورماتور است. شکل ۵ را میتوان با قرار دادن $$t=1/a$$ و تعویض دو شین $$i$$ و $$j$$ از شکل ۴ بهدست آورد.
با معرفی اجزای موجود در خطوط انتقال، اکنون میتوانیم مطالعه نظاممند یک سیستم قدرت $$n$$ شینه را شروع کنیم. برای این منظور، ابتدا مفهوم توان و جریان تزریقی را بیان میکنیم.
مفهوم توان و جریان تزریقی
همانگونه که از نام توان (جریان) تزریقی پیداست، مقدار توان (جریانی) است که در «به» یک شین تزریق یا وارد میشود. برای درک بهتر، شکل ۶ را در نظر بگیرید. در بخش (الف) این شکل، یک ژنراتور به شین متصل شده و هر دو توان اکتیو و راکتیو را به آن تزریق میکند. جریان شین نیز برابر با جریان تزریقی ژنراتور است. از سوی دیگر، باری که به یک شین متصل است (شکل 6 (ب))، از نظر فیزیکی توان اکتیو (راکتیو) را مصرف میکند. بنابراین، توان اکتیو (راکتیو) تزریقی به شین، قرینه (منفی) توان اکتیو (راکتیو) مصرفی بار است. بهطریق مشابه، علامت جریان مصرفی و تزریقی در این شین، مخالف یکدیگر است.
اگر ژنراتور و بار، هر دو به یک شین متصل باشند (شکل 6 (ج))، توان اکتیو (راکتیو) خالصی که به شین تزریق میشود، برابر با توان اکتیو (راکتیو) ژنراتور منهای توان اکتیو (راکتیو) مصرفی بار است. بهطریق مشابه، جریان تزریقی خالص در این حالت، برابر با اختلاف جریان ژنراتور و جریان بار است.
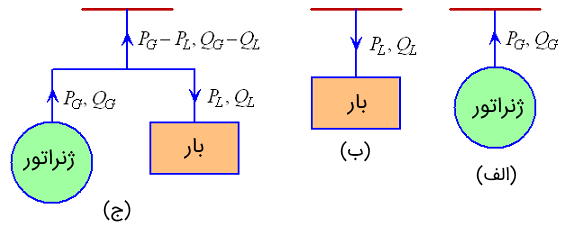
بهعنوان جمع بندی میتوان گفت در صورتی که $$P_k$$، $$Q_k$$ و $$\bar{I}_k$$ بهترتیب، توان حقیقی، توان راکتیو و جریان مختلط شین دلخواه $$k$$ را نشان دهند:
- اگر فقط یک ژنراتور به شین $$k$$ وصل شود، آنگاه داریم: $$P_k=P_G$$، $$Q_k=Q_G$$ و $$\bar{I}_k=\bar{I}_G$$.
- اگر فقط یک بار به شین $$k$$ وصل شود، آنگاه داریم: $$P_k=-P_L$$، $$Q_k=-Q_L$$ و $$\bar{I}_k=-\bar{I}_L$$.
- اگر هم ژنراتور و هم بار به شین $$k$$ متصل باشد، آنگاه داریم: $$P_k=P_G-P_L$$، $$Q_k=G_G-Q_L$$ و $$\bar{I}_k=\bar{I}_G-\bar{I}_L$$.
- اگر هیچ بار و ژنراتوری به شین $$k$$ متصل نباشد، آنگاه داریم: $$P_k=0$$، $$Q_k=0$$ و $$\bar{I}_k=0$$.
اکنون که مفهوم توان و جریان تزریقی را میدانیم، میتوانیم تحلیل هر سیستم قدرت $$n$$ شینه را انجام دهیم. برای این کار، ابتدا ماتریس ادمیتانس را بهدست میآوریم.
تشکیل ماتریس ادمیتانس شین ($$\mathrm{\bar{Y}_{BUS}}$$)
شبکه پنجشینه شکل ۷ را در نظر بگیرید. در این شبکه، همه خطوط انتقال با مدل $$\pi$$ نشان داده میشوند. در نتیجه، مدار معادل آن مطابق شکل ۸ است.
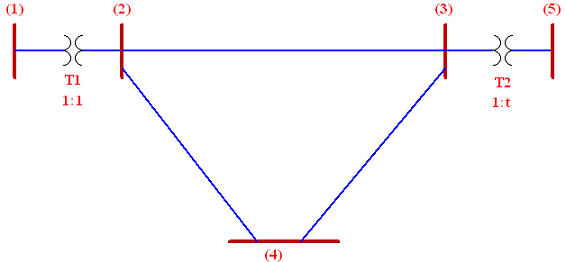
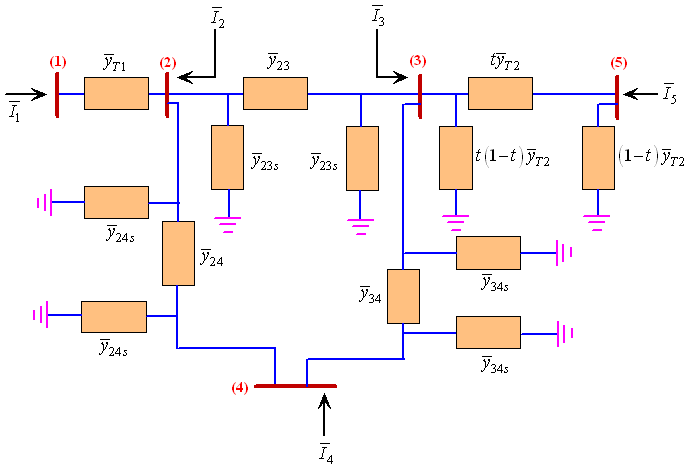
در شکل ۸، $$\bar{I}_k$$ (برای $$k=1,2,3,4,5$$) جریانهای تزریقی در شین $$k$$ هستند. همچنین، کمیت $$\bar{y}_{ij}$$ ادمیتانس سری خط $$i-j$$ را نشان میدهد، در حالی که $$\bar{y}_{ijs}$$، نشاندهنده سوسپتانس نصف خط $$i-j$$ است. اکنون با اعمال KCL در هریک از k شین، داریم:
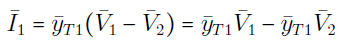
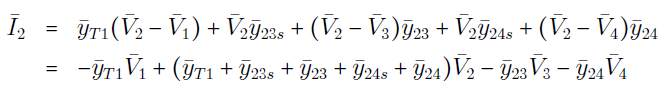
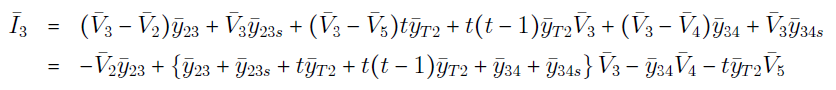
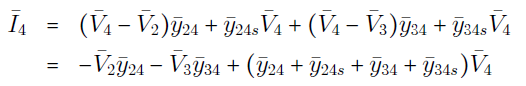
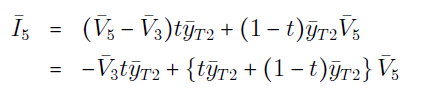
روابط (۱) تا (۵) را میتوان بهفرم ماتریسی زیر نشان داد:
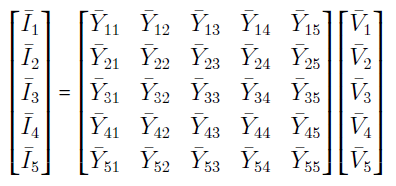
که در آن:
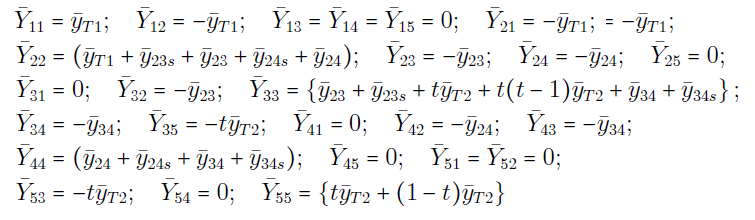
معادله (۶) را نیز میتوان بهصورت زیر نوشت:
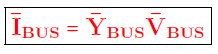
که در آن،
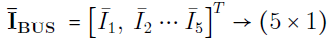
و
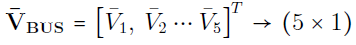
به ترتیب، بردار جریانهای تزریقی شین و بردار ولتاژ شینها نسبت به زمین هستند. همچنین،
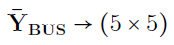
ماتریس ادمیتانس شین است.
از درایههای ماتریس ادمیتانس $$\mathrm{\bar{Y}_{BUS}}$$ میتوان به نکات زیر برای $$i=1,2, \ldots,5$$ اشاره کرد:
- $$\bar{Y}_{ii}$$ برابر با مجموع همه ادمیتانسهای متصل به شین $$i$$ است.
- $$\bar{Y}_{ij}$$ برابر با منفی ادمیتانس بین شین $$i$$ و شین $$j$$ است (اگر اتصال فیزیکی داشته باشند).
- اگر ارتباط فیزیکی بین دو شین $$i$$ و $$j$$ وجود نداشته باشد، آنگاه $$\bar{Y}_{ij}=0$$.
به طریق مشابه، برای یک سیستم قدرت با $$n$$ شین، رابطه (۷) برقرار است و در آن،
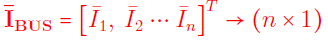
و
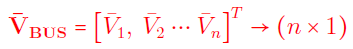
و
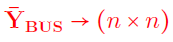
بهترتیب، بردار جریانهای تزریقی شین، بردار ولتاژ شین و ماتریس ادمیتانس شین هستند.
درایههای ماتریس $$\mathrm{\bar{Y}_{BUS}}$$ مطابق روشی که در بالا گفته شد بهدست میآیند.
تا اینجا روش تشکیل ماتریس $$\mathrm{\bar{Y}_{BUS}}$$ را بدون حضور تزویج گفتیم. در ادامه، نحوه تشکیل این ماتریس را در حالتی که تزویج متقابل بین اجزایش شبکه وجود داشته باشد بیان خواهیم کرد.
تشکیل ماتریس ماتریس $$\mathrm{\bar{Y}_{BUS}}$$ با حضور تزویج متقابل بین اجزای شبکه
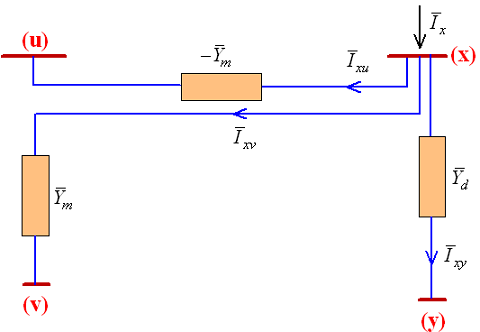
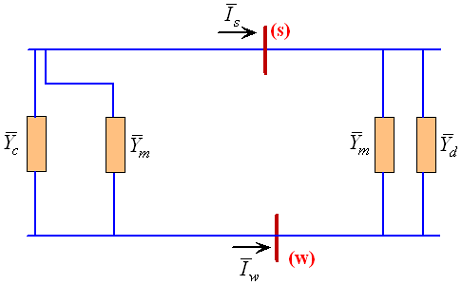
در شکل 9، امپدانس $$\bar{Z}_c$$ که بین دو گره u و v قرار گرفته است، با امپدانس $$\bar{Z}_d$$ که بین دو گره x و y واقع شده، از طریق امپدانس $$\bar{Z}_m$$ تزویج متقابل دارد.
جریان گذرنده از امپدانسها، ولتاژ آنها و جریانهای تزریقی هر چهار گره در شکل 9 نشان داده شدهاند.
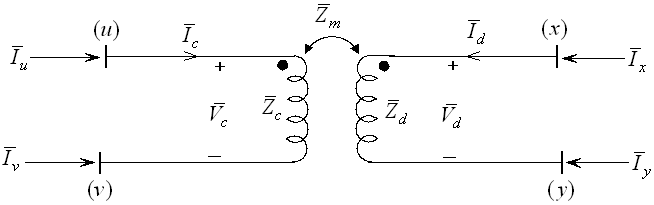
با توجه به شکل ۹ میتوان رابطه بین ولتاژها و جریانهای متناظر با هر دو امپدانس را بهصورت زیر بیان کرد:
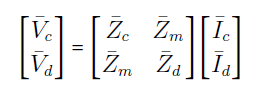
یا
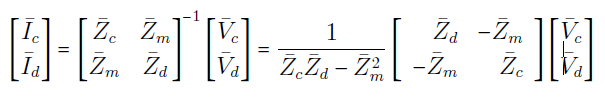
یا
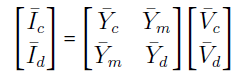
که در آن:
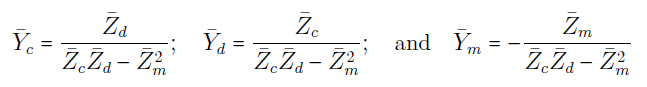
با توجه به شکل ۹ میتوان رابطه زیر را نوشت:
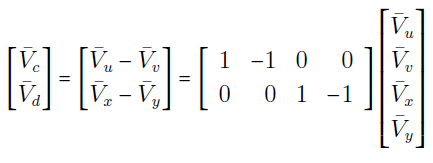
یا
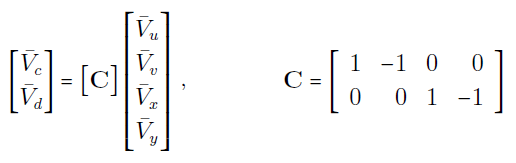
باز هم با توجه به شکل 9 داریم:
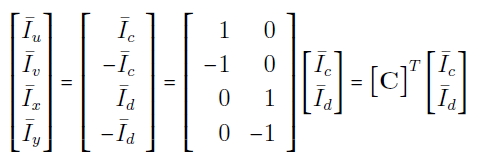
معادلات (۸) و (۱۰)، منجر به رابطه زیر میشود:
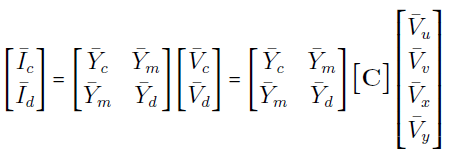
یا
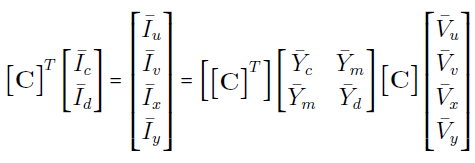
اکنون میتوانیم رابطه زیر را بنویسیم:
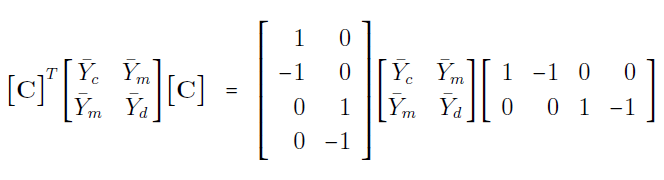
یا
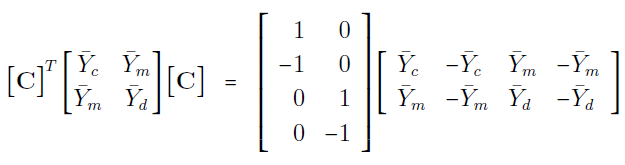
یا
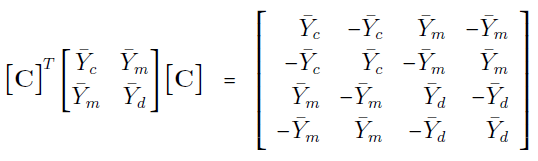
بنابراین، از روابط (۱۲) و (۱۵) داریم:
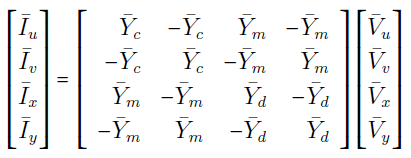
از رابطه (۱۶) میتوان نوشت:
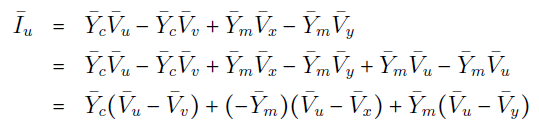
یا
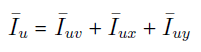
بهطور مشابه داریم:
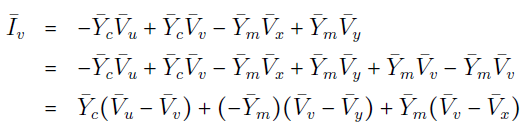
یا
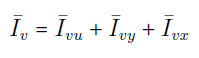
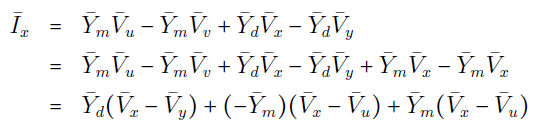
یا
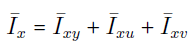
معادلات (۱۸)، (۲۰) و (۲۲) را میتوان بهترتیب، با شبکههای جزئی شکلهای 10، 11 و 12 نمایش داد. با ترکیب شکلهای 10، 11 و 12، شکل ۱۳ بهدست میآید.
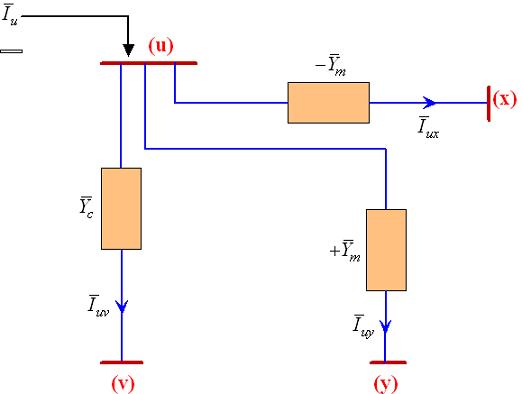
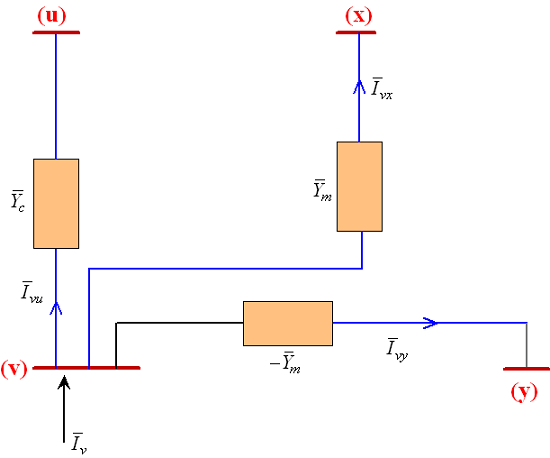
از سطر آخر رابطه (۱۶) میتوان نوشت:
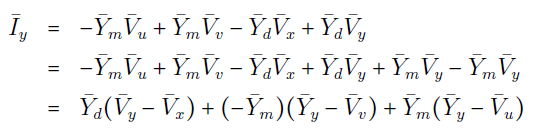
رابطه (۲۳) را میتوان در شکل 13 مشاهده کرد. بنابراین، رابطه ولتاژ-جریان در معادله (۱۶)، در شکل 13 قابل مشاهده است. شکل 13 را میتوان بهعنوان مدار معادل شکل 9 در نظر گرفت. از آنجایی که شکل 13 ادمیتانس متقابل ندارد، ماتریس $$\mathrm{\bar{Y}_{BUS}}$$ را میتوان با کمک این شکل تشکیل داد.
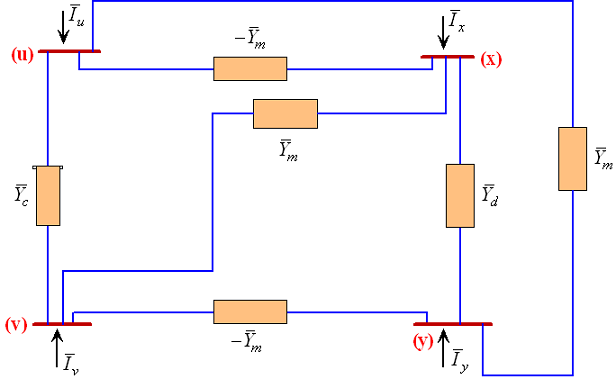
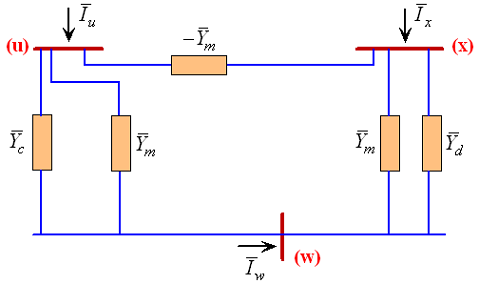
شکل 13، عمومیترین حالت را نشان میدهد که در آن، هر چهار گره مجزا از هم هستند. هرچند در بسیاری از موارد، تزویج متقابل بین دو عنصر برقرار است که یک گره مشترک بین آنها وجود دارد. در این حالت، مدار معادل را میتوان از شکل 13 بهدست آورد. برای مثال، در شکل 13، اگر گرههای v و y مشترک باشند (w)، آنگاه مدار معادل مطابق شکل 14 خواهد بود. علاوه بر این، اگر گرههای u و x مشترک باشند (s)، مدار معادل مطابق شکل 15 است. با استفاده از دو شکل 14 و 15 نیز میتوان ماتریس ادمیتانس را بهدست آورد.
معادله اساسی پخش بار
از معادله (۷) برای یک سیستم با $$n$$ شین، داریم:
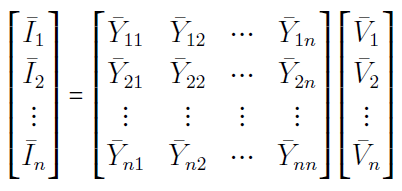
یا
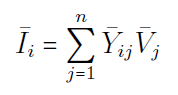
توان مختلط تزریقی در شین i با رابطه زیر تعیین میشود:
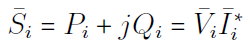
اکنون، مقادیر زیر را در نظر بگیرید:
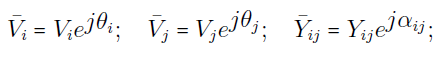
در نتیجه، داریم:
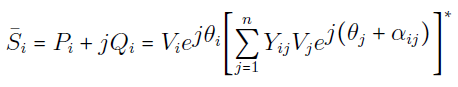
یا
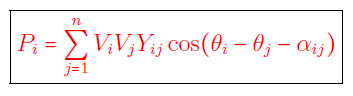
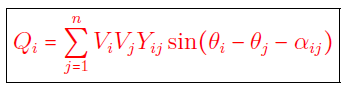
معادلات (۲۷) و (۲۸) بهعنوان معادلات اساسی پخش بار شناخته میشوند. میتوان دید که برای شین $$i$$اُم، دو معادله وجود دارد. بنابراین، برای یک سیستم قدرت با $$n$$ شین، تعداد $$2n$$ معادله پخش بار داریم. از معادلات (۲۷) و (۲۸) میتوان دریافت که در شین $$i$$اُم، چهار متغیر $$V_i$$، $$\theta _i$$، $$P_i$$ و $$Q_i$$ وجود دارد. بنابراین، در یک سیستم با $$n$$ شین، تعداد $$4n$$ متغیر داریم. از آنجایی که فقط $$2n$$ معادله از این $$4n$$ متغیر در دسترس داریم، باید $$2n$$ متغیر را تعیین و $$2n$$ کمیت باقیمانده را از $$2n$$ معادله پخش بار بهدست آوریم. همچنین، از آنجایی که باید $$2n$$ متغیر را در یک سیستم $$n$$ شینه تعیین کنیم، در هر شین باید دو کمیت تعیین شود. بدین منظور، شینهای یک سیستم را به سه دسته مختلف تقسیم میکنیم که در هر دسته، دو کمیت شین، معلوم است.
- شین PQ: به این شینها بار متصل است، به همین دلیل، آنها را بهعنوان شینهای بار نیز میشناسند. عموماً مقادیر توان اکتیو و راکتیو بارهای متصل به این نوع شینها معلوم است، بنابراین، در این شینها، $$P_i$$ و $$Q_i$$ مشخص یا معلوم است. در نتیجه، $$V_i$$ و $$\theta _i$$ این شینها را باید محاسبه کرد.
- شین PV: در عمل، به این نوع شینها ژنراتور متصل است. عموماً توان اکتیو ژنراتور مشخص است و اندازه ولتاژ ترمینال ژنراتور نیز توسط سیستم تحریک آن، بهصورت پیشفرض ثابت نگه داشته میشود. بنابراین، در یک شین PV، مقادیر $$P_i$$ و $$V_i$$ مشخص است، در نتیجه باید $$Q_i$$ و $$\theta _i$$ را محاسبه کرد.
- شین اسلک یا شناور: برای محاسبه زوایای $$\theta _i$$، لازم است یک زاویه مرجع ($$\theta _i=0$$) تعیین کرد و زاویه ولتاژها را نسبت به آن سنجید. علاوه بر این، توان کل تولیدی باید برابر با مجموع مصارف بارها و تلفات سیستم باشد. هرچند، از آنجایی که نمیتوان تلفات سیستم را قبل از محاسبات پخش بار بهدست آورد، توان اکتیو خروجی همه ژنراتورهای سیستم را نمیتوان از قبل مشخص کرد. در این حالت، باید حداقل یک ژنراتور از سیستم، تلفات را تأمین یا جبران کند (علاوه بر تأمین بار). بنابراین، نمیتوان مقدار توان اکتیو تولیدی این ژنراتور را از قبل تعیین کرد. البته، بهدلیل عملکرد سیستم تحریک، مقدار $$V_i$$ ژنراتور را میتوان مشخص کرد. در نتیجه، مقادیر $$V_i$$ و $$\theta _i$$ ژنراتور از پیش تعیین شدهاند و باید $$P_i$$ و $$Q_i$$ را برای آن محاسبه کرد. این شین که بهعنوان شین شناور طراحی میشود، معمولاً شین متصل به بزرگترین ژنراتور سیستم است.
بهعنوان جمعبندی، میتوان جزئیات انواع مختلف شینها را در یک سیستم با $$n$$ شین و $$m$$ ژنراتور در جدول ۱ بیان کرد.
جدول ۱: دسته بندی شینها
| نوع | تعداد شینها | مقادیر معلوم | مقادیر مجهول |
| PQ | $$n-m$$ | $$P_i$$ و $$Q_i$$ | $$V_i$$ و $$\theta _i$$ |
| PV | $$m-1$$ | $$P_i$$ و $$V_i$$ | $$Q_i$$ و $$\theta _i$$ |
| شناور | $$1$$ | $$V_i$$ و $$\theta _i$$ | $$P_i$$ و $$Q_i$$ |
باید توجه کرد که مقادیر $$P_i$$ و $$Q_i$$ ($$Q_i$$ در شین PV و $$P_i$$ و $$Q_i$$ در شین شناور) را نمیتوان مستقیماً بهدست آورد. فقط مقادیر $$V_i$$ و $$\theta _i$$ ($$V_i$$ برای همه شینهای PQ و $$\theta _i$$ برای همه شینهای PV و PQ) را میتوان مستقیماً محاسبه کرد. دلیل این امر، این واقعیت است که وقتی $$V_i$$ و $$\theta _i$$ برای برای همه شینهای PV و PQ بهدست آمدند، آنگاه اندازه و زاویه ولتاژ باسها ($$V_i$$ و $$\theta _i$$ در شین شناور قبلاً تعیین شدهاند) معلوم خواهد شد. در نتیجه، با استفاده از معادلات (۲۷) و (۲۸)، $$P_i$$ و $$Q_i$$ قابل محاسبه است.
بنابراین، در یک سیستم با $$n$$ شین و $$m$$ ژنراتور، مقادیر مجهول عبارتند از: $$V_i$$ (که تعداد آنها $$n-m$$ است) و $$\theta _i$$ (که تعداد آنها $$n-1$$ است). در نتیجه، تعداد مقادیر مجهول، $$2n-m-1$$ است. از سوی دیگر، مقادیر معلوم عبارتند از: $$P_i$$ (که تعداد آنها $$n-1$$ است) و $$Q_i$$ ( که تعداد آنها $$n-m$$ است). بنابراین، تعداد کل متغیرهای معلوم، $$2n-m-1$$ است. از آنجایی که تعداد کمیتهای معلوم با مجهول برابر است، مسئله پخش بار، یک مسئله خوشتعریف است.
معادلات (۲۷) و (۲۸)، مجموعهای از معادلات جبری، غیرخطی و چندمجهولی را نشان میدهند. از آنجایی که مجموعه معادلات، غیرخطی است، حلِ تحلیلی و مشخصی برای آن وجود ندارد. در نتیجه، این معادلات را تنها میتوان با استفاده از روشهای تکراری عددی حل کرد. برای حل اینگونه معادلات، روشهای تکراری مختلفی وجود دارد که عبارتند از:
- روش گوس-سایدل
- روش نیوتن-رافسون (قطبی)
- روش نیوتن -رافسون (دکارتی)
- پخش بار تفکیکشده سریع
در آموزشهای بعدی، درباره روش حل معادلات پخش بار با استفاده از این روشها بحث خواهیم کرد.
اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:
- آموزش بررسی سیستم های قدرت 2
- آموزش شبیه سازی سیستم های قدرت با PowerWorld Simulator
- آموزش نرم افزار DIgSILENT برای آنالیز و شبیه سازی سیستم های قدرت
- پایداری سیستم قدرت — به زبان ساده
- پخش بار نیوتن رافسون در متلب — از صفر تا صد
^^











سلام وقت بخیر سوالی داشتم
در شبکه ۲۴ باسه یا بالاتر در برنامه مت پاور هر جا که ترانسی وجود دارد سوسبتانس ان را صفر در نظر میگیرند چرا