محاسبه جریان سیال — به زبان ساده

در این آموزش، نحوه محاسبه جریان سیال در لوله را بیان می‌‌کنیم.

قانون توریچلی (Torricelli’s Law)

دانشمند ایتالیلیی، اوانجلیستا توریچلی (Evangelista Torricelli)، جریان سیال را به صورت تجربی مشاهده کرد و در سال ۱۶۴۳ پی برد که سرعت جریان خارج شدن یک سیال از یک سوراخ کوچک در کف یک مخزن باز (شکل ۱)، با فرمول زیر بیان می‌شود:

$$\large v = \sqrt { 2 g h } ,$$

فیلم آموزش هیدرودینامیک – جامع و با حل مثال مختلف در فرادرس

کلیک کنید

که در آن، $$h$$ ارتفاع سیال از بالای ظرف است و $$g$$ شتاب گرانشی را نشان می‌دهد.

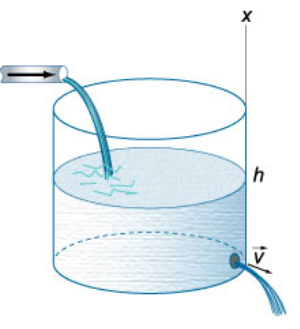
فرمول مشابهی سرعت یک ذره جامد آزاد را توصیف می‌کند که در ارتفاع $$h$$ در میدان گرانشی زمین در یک فضای خلأ‌ رها می‌شود. البته، این فرمول سرعت کاملاً دقیق نیست. در حقیقت، سرعت سیال به شکل و اندازه دهانه، ویسکوزیته سیال و مد جریان بستگی دارد. بنابراین، فرمول توریچلی اغلب با ضریب اضافه $$\varphi$$ نوشته می‌شود:

$$\large v = \varphi \sqrt { 2 g h } ,$$

که ضریب $$\varphi$$ نزدیک به ۱ است. مقادیر ضریب $$\varphi$$ برای دهانه‌‌هایی با شکل و اندازه متفاوت در کتاب‌های هیدرولیک بیان می‌شود.

محاسبه جریان سیال یک لوله نازک طویل

جریان سیال یک لوله نازک طویل (شکل ۲) تعدادی ویژگی دارد.

فیلم آموزش مدل سازی و شبیه سازی جریان سیال در محیط متخلخل با متلب در فرادرس

کلیک کنید

اثرات مویینگی مختلف ناشی از تنش سطح و رطوبت‌پذیری در اثر تماس با دیواره لوله نقش مهمی دارد.

سرعت سیال که از لوله‌های مویرگی بیرون می‌آید، تقریباً متناسب با ارتفاع سیال از دهانه لوله است:

$$\large v = kh,$$

که در آن، $$k$$ یک ثابت مشخص وابسته به ویسکوزیته سیال و هندسه و جنس لوله است.

در ادامه، جریان سیال را با استفاده از معادلات دیفرانسیل برای هر دو نوع لوله بیان می‌کنیم.

معادله دیفرانسیل جریان سیال خروجی

معادله دیفرانسیل جریان سیال را می‌توان با توجه به تعادل سیال در یک لوله به دست آورد.

فیلم آموزش مقدماتی مکانیک سیالات ۲ در فرادرس

کلیک کنید

به عنوان یک مثال، یک ظرف استوانه‌ای را در نظر بگیرید که شعاع آن $$R$$ است. فرض کنید سیال از یک دهانه کوچک به شعاع $$a$$ از کف ظرف خارج می‌شود (شکل ۳).

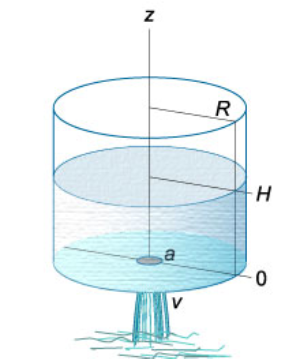
سرعت سیال با فرمول توریچلی به صورت زیر توصیف می‌شود:

$$\large v = \sqrt {2gz} ,$$

که در آن، $$z$$ ارتفاع سطح سیال از بالای دهانه ظرف است. بنابراین، جریان سیال به صورت زیر خواهد بود:

$$\large q = – \pi { a ^ 2 } \sqrt { 2 g z } .$$

در این فرمول، $$\pi a ^ 2$$ متناظر با مساحت دهانه است که سیال از آن خارج می‌شود و علامت منفی به این معنی است که ارتفاع سیال هنگامی که از مخزن بیرون می‌ریزد کاهش می‌یابد.

معادله تعادل سیال در مخزن به صورت زیر است:

$$\large \frac{{dV}}{{dt}} = q.$$

از آنجایی که تغییر حجم $$dV$$ را می‌توان به صورت زیر بیان کرد:

$$\large dV = S\left( z \right)dz,$$

معادله دیفرانسیل زیر را خواهیم داشت:

$$\large \frac { { S \left ( z \right ) d z } } { { d t } } = q \left ( z \right ) .$$

با قرار دادن $$q\left( z \right)$$ در معادله بالا، داریم:

$$\large \frac { { S \left ( z \right ) d z } } { { d t } } = – \pi { a ^ 2 } \sqrt { 2 g z } .$$

سطح مقطع $${S\left( z \right)}$$ مخزن استوانه‌ای به ارتفاع $$z$$ وابسته نیست و به صورت زیر است:

$$\large S \left ( z \right ) = \pi { R ^ 2 } ,$$

که در آن، $$R$$ شعاع قاعده استوانه است. در نتیجه، داریم:

$$ \large \require {cancel} \cancel { \pi } { R ^ 2 } \frac { { d z } } { { d t } } = – \cancel { \pi } { a ^ 2 } \sqrt { 2 g z } . $$

بنابراین، معادله جداشدنی زیر را خواهیم داشت:

$$\large \frac { { d z } } { { \sqrt z } } = – \frac { { { a ^ 2 } } } { { { R ^ 2 } } } \sqrt { 2 g } d t .$$

اکنون با فرض ارتفاع اولیه $$H$$ و اینکه سطح سیال از ۰ تا $$T$$ تغییر می‌کند، از معادله انتگرال می‌گیریم:

$$\large \begin {align*} & \int \limits _ H ^ 0 { \frac { { d z } } { { \sqrt z } } } = – \int \limits _ 0 ^ T { \frac { { { a ^ 2 } } } { { { R ^ 2 } } } \sqrt { 2 g } d t } , \; \; \Rightarrow { { 2 \left [ { \left . { \left ( { \sqrt z } \right ) } \right | _ H ^ 0 } \right ] } = { – \frac { { { a ^ 2 } } } { { { R ^ 2 } } } \sqrt { 2 g } \left [ { \left . { \left ( t \right ) } \right | _ 0 ^ T } \right ] , \; \; } } \\ & \Rightarrow { 2 \sqrt H = \frac { { { a ^ 2 } } }{ { { R ^ 2 } } } \sqrt { 2 g } T, \; \; } \Rightarrow { \sqrt { 2 H } = \frac { { { a ^ 2 } } } { { { R ^ 2 } } } \sqrt g T . } \end {align*}$$

رابطه اخیر نتیجه می‌دهد که $$T$$ به صورت زیر است:

$$\large T = \frac { { { R ^ 2 } } } { { { a ^ 2 } } } \sqrt { \frac { { 2 H } } { g } } .$$

جالب است که فرمول حاصل برای حالت $$a = R$$ (وقتی مقاطع عرضی دهانه و استوانه با هم برابر باشند) به فرمول شناخته شده ‍$$T = \sqrt {\large\frac{{2H}}{g}\normalsize}$$ تبدیل می‌شود که زمان سقوط یک ذره جامد را از ارتفاع $$H$$ نشان می‌دهد.

وابستگی زمان $$T$$ به ارتفاع $$H$$ به صورت شماتیکی در شکل ۴ نشان داده شده است.

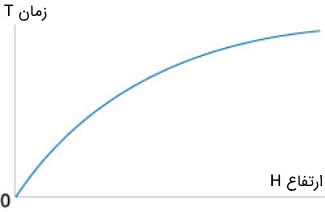
به طور مشابه، می‌توانیم جریان سیال لوله‌هایی به شکل دیگر را نیز توصیف کنیم. برای آشنایی با چگونگی شبیه‌سازی جریان سیال می‌توانید به مجموعه آموزش مدلسازی و شبیه سازی مقدماتی تا پیشرفته فرادرس مراجعه کنید.

مثال‌ها

در این بخش، دو مثال ساده از محاسبه جریان سیال را بررسی می‌کنیم.

فیلم آموزش جریان لزج یا ویسکوز در فرادرس

کلیک کنید

مثال ۱

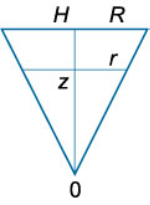
معادله دیفرانسیل نشتی سیالی را به دست آورید که درون یک مخروط است. همچنین زمان کل $$T$$ جریان سیال را بیابید. شعاع قاعده بالایی ظرف مخروطی برابر با $$R$$ و شعاع قاعده پایینی آن $$a$$ است. ارتفاع اولیه سیال را $$H$$ در نظر بگیرید (شکل ۵).

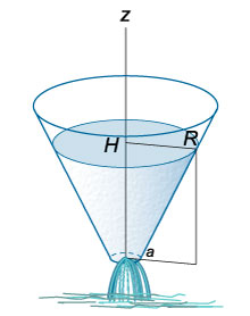
حل: تغییر سطح سیال در ارتفاع $$z$$ با معادله دیفرانسیل زیر بیان می‌شود:

$$\large S \left ( z \right ) \frac { { d z } } { { d t } } = q \left ( z \right ) ,$$

که در آن، $$S ( z )$$ مساحت سطح مقطع در ارتفاع $$z$$ و $$q ( z )$$ جریان سیال است که به ارتفاع $$z$$ بستگی دارد.

بر اساس هندسه سیستم، می‌توانیم فرض کنیم که قانون توریچلی برقرار است. بنابراین، می‌توان نوشت:

$$\large q \left ( z \right ) = – \pi { a ^ 2 } \sqrt { 2 g z } ,$$

که در آن، $$a$$ شعاع دهانه در کف مخروط است. با توجه به اینکه این دهانه به اندازه کافی کوچک است، می‌توانیم سطح مقطع مخروط را به صورت یک مثلث در نظر بگیریم (شکل ۶). بر اساس تشابه مثلث‌ها نیز می‌توان نوشت:

$$\large \frac { R } { H } = \frac { r } { z } .$$

بنابراین، مساحت سطح سیال در ارتفاع $$z$$ برابر است با:

$$\large { S \left ( z \right ) = \pi { r ^ 2 } } = { \pi { \left ( { \frac { { R z } } { H } } \right ) ^ 2 } } = { \frac { { \pi { R ^ 2 } { z ^ 2 } } } { { { H ^ 2 } } } . }$$

با قرار دادن $$S\left( z \right)$$ و $$q\left( z \right)$$ در معادله دیفرانسیل، داریم:

$$\large { \frac { { \pi { R ^ 2 } { z ^ 2 } } } { { { H ^ 2 } } } \frac { { d z } } { { d t } } } = { – \pi { a ^ 2 } \sqrt { 2 g z } . }$$

پس از تعدادی عملیات ریاضی، معادله دیفرانسیل زیر را خواهیم داشت:

$$\large { { z ^ { \large \frac { 3 } { 2 } \normalsize } } d z } = { – \frac { { { a ^ 2 } { H ^ 2 } } } { { { R ^ 2 } } } \sqrt { 2 g } d t . }$$

با انتگرال‌گیری از دو طرف معادله بالا و با در نظر گرفتن سطحی که سیال از نقطه اولیه $$H$$ در زمان $$T$$ به $$0$$ کاهش پیدا می‌کند، داریم:

$$\large \begin {align*} & \int \limits _ H ^ 0 { { z ^ { \large \frac { 3 } { 2 } \normalsize } } d z } = { – \int \limits _ 0 ^ T { \frac { { { a ^ 2 } { H ^ 2 } } } { { { R ^ 2 } } } \sqrt { 2 g } d t } ,\; \; } \\ & \Rightarrow { { \left . { \left ( { \frac { { { z ^ { \large \frac { 5 }{ 2 } \normalsize } } } } { { \frac { 5 } { 2 } } } } \right ) } \right | _ 0 ^ H } = { \frac { { { a ^ 2 } { H ^ 2 } } }{ { {R ^ 2 } } } \sqrt { 2 g } \left [ { \left . { \left ( t \right ) } \right | _ 0 ^ T } \right ] , \; \; } } \\ & \Rightarrow { \frac { 2 } { 5 } { H ^ { \large \frac { 5 } { 2 } \normalsize } } = \frac { { { a ^ 2 } { H ^ 2 } } } { { { R ^ 2 } } } \sqrt { 2 g } T , \; \; } \\ & \Rightarrow { \frac { 1 } { 5 } \sqrt { \frac { { 2 H } } { g } } = \frac { { { a ^ 2 } } } { { { R ^ 2 } } } T , \; \; } \\ & \Rightarrow { T = \frac { { { R ^ 2 } } } { { 5 { a ^ 2 } } } \sqrt { \frac { { 2 H } } { g } } . } \end {align*}$$

در اینجا می‌توانیم این مسئله را با سقوط یک جسم از ارتفاع $$H$$ مقایسه کنیم. همان‌طور که می‌دانیم، زمان سقوط برابر است با:

$$\large T = \sqrt { \frac { { 2 H } } { g } } .$$

اگر این نتیجه را با حالتی که در آن، سیال از یک استوانه خارج می‌شود،‌ مقایسه کنیم، خواهیم دید که با مقادیر مشابه $$H$$، $$R$$ و $$a$$، خالی شدن مخروط ۵ برابر سریع‌تر از خالی شدن استوانه رخ می‌دهد (در حالی که حجم سیال ظرف مخروطی تنها سه برابر کوچک‌تر از حجم استوانه است). چنین نسبت‌هایی صحیحی بسیار جالب هستند. این‌طور نیست؟

مثال ۲

جریان سیال یک لوله نازک با شعاع $$R$$ و ارتفاع $$H$$ را با فرض اینکه لوله کاملاً‌ پر شده باشد به دست آورید.

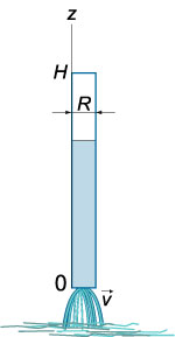
حل: مشابه مثال قبل، می‌توانیم معادله تعادل سیال را در ارتفاع دلخواه $$z$$ به فرم زیر بنویسیم:

$$\large S \left ( z \right ) \frac { { d z } } { { d t } } = q \left ( z \right ) .$$

در این حالت، مساحت سطح مقطع $$S\left( z \right)$$ ثابت است:

$$\large S \left ( z \right ) = S = \pi { R ^ 2 }$$

و جریان سیال خروجی لوله با فرمول زیر تعیین می‌شود:

$$\large q \left ( z \right ) = – k z$$

که در آن، $$k$$ به اندازه دهانه لوله، رطوبت‌پذیری آن و سایر پارامترها بستگی دارد.

در نتیجه، معادله ساده زیر به دست می‌آید:

$$\large \pi { R ^ 2 } \frac { { d z } } { { d t } } = – k z$$

این معادله را می‌توان به صورت زیر بازنویسی کرد:

$$\large \frac { { d z } } { z } = – \frac { k } { { \pi { R ^ 2 } } } d t .$$

اکنون می‌توان با فرض اینکه سطح سیال از زمان $$0$$ تا $$t$$، از $$H$$ به $$h$$ کاهش می‌یابد، از آن انتگرال گرفت:

$$\large \begin {align*} & \int \limits _ H ^ h { \frac { { d z } } { z } } = – \int \limits _ 0 ^ t { \frac { k } { { \pi { R ^ 2 } } } d t } ,\; \; \Rightarrow { \left . { \left ( { \ln z } \right ) } \right | _ h ^ H = \frac { k } { { \pi { R ^ 2 } } } t , \; \; } \\ & \Rightarrow { t = \frac { { \pi { R ^ 2 } } } { k } \left ( { \ln H – \ln h } \right ) } = { \frac { { \pi { R ^ 2 } } } { k } \ln \frac { H } { h } . } \end {align*}$$

وابستگی $$t$$ به نسبت $$\frac { H} { h }$$ به طور شماتیکی در شکل ۸ نشان داده شده است. این منحنی، مشابه منحنی وابستگی زمان $$T$$ به ارتفاع $$H$$ برای یک لوله یا مخزن استوانه‌ای عریض است که قانون توریچلی در آن برقرار است.

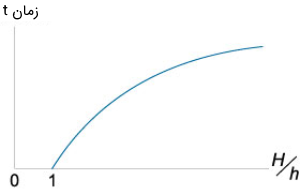
جالب است که وقتی زمان $$t$$ جریان سیال به بینهایت میل کند، ارتفاع $$h$$ نیز به صفر خواهد رسید.

اگر این مطلب برای شما مفید بوده است، آموزش‌ها و مطالب زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های مکانیک سیالات
• آموزش مکانیک سیالات (مرور و حل تست کنکور ارشد)
• مجموعه آموزش‌های دروس مهندسی مکانیک
• معادله دیفرانسیل برنولی — از صفر تا صد
• پیوستگی و بقای جرم در سیالات — از صفر تا صد
• سینماتیک سیالات — مقدمه‌ای بر مکانیک
• استاتیک سیالات — به زبان ساده

^^