استاتیک سیالات — به زبان ساده

استاتیک سیالات، شاخه‌ای از علم مکانیک است که به بررسی سیال ساکن و یا سیالی می‌پردازد که به صورت جسم صلب حرکت می‌کند. حرکت به صورت جسم صلب یعنی این‌ که ذرات سیال نسبت به یکدیگر ساکن باشند. در سیال ساکن، تنش برشی وجود نخواهد داشت، بنابراین ذرات سیال، تغییر شکل نخواهند داد. در استاتیک سیالات، فقط با تنش قائم و فشار مواجه هستیم.

فیلم آموزش ایستایی (استاتیک) – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

به منظور بررسی تاثیر نیروی وارد شده به ذرات سیال، از قانون دوم نیوتن استفاده می‌کنیم. ذره‌ای از سیال را مطابق شکل زیر در نظر می‌گیریم.

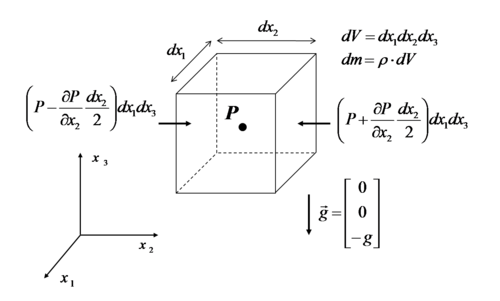
ذره سیال و نیروهای وارد شده به آن

قانون دوم نیوتن در جهت i برابر است با:

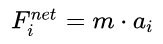
این نیرو می‌تواند به دو دسته نیروی سطحی و حجمی تقسیم‌بندی شود. بنابراین:

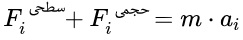
همچنین نیروی ناشی از فشار معادل است با:

اندازه بردار A برابر با سطحی در نظر گرفته می‌شود که فشار سیال روی آن قرار می‌گیرد و جهت این بردار، ‌عمود بر همین سطح است. با توجه به این فرضیات، می‌توان نوشت:

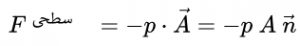
بر مبنای نیروهای معرفی شده، قانون دوم نیوتن برای ذره سیال را می‌توان به صورت زیر نوشت:

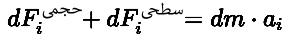
P، فشار در مرکز ذره در نظر گرفته شده است؛ بنابراین به منظور محاسبه این مقدار روی سطح، می‌توان از تعریف مشتق استفاده کرد. در نتیجه فشار روی سطح و در فاصله dx/2 از مرکز، برابر است با:

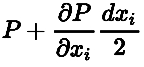
یا به عبارت دیگر:

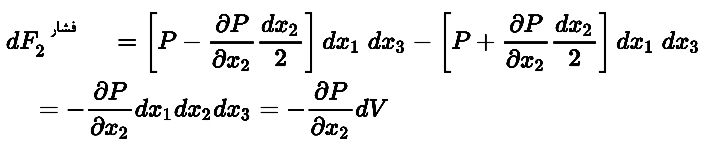
بنابراین:

نهایتاً می‌توان تغییرات فشار در راستاهای مختلف را به صورت زیر محاسبه کرد:

$$\large \begin{aligned}
&-\frac{\partial P}{\partial x_{i}} d V+d m g_{i}=d m a_{i} \text { or, }-\frac{\partial P}{\partial x_{i}} d V+\rho\ d V g_{i}=\rho\ dV\ a_{i} \\
&\text{or}\ ,-\frac{\partial P}{\partial x_{i}}+\rho g_{i}=\rho a_{i} \\
&\text{or}\ ,-\frac{\partial P}{\partial x_{1}}=\rho a_{1} ;-\frac{\partial P}{\partial x_{2}}=\rho a_{2} ;-\frac{\partial P}{\partial x_{3}}-\rho g=\rho a_{3}
\end{aligned}$$

معادله بالا، گرادیان فشار در جهات مختلف را بیان می‌کند؛ با برابر قرار دادن سمت راست معادلات بالا با شتاب، تغییرات فشار قابل محاسبه هستند. بنابراین برای حالتی که فقط نیروی گرانش وجود دارد، معادله بالا به شکل زیر قابل بیان است:

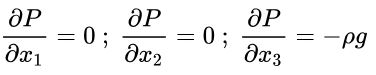
در معادله بالا فرض شده که سیال در راستای x و y شتابی ندارد. بنابراین فقط شتاب در راستای z (همان شتاب گرانشی) است که در این معادلات ظاهر شده.

توزیع فشار در سیال غیر قابل تراکم

همان طور که در بخش قبل بیان کردیم، گرادیان فشار در هر جهت وابسته به شتاب در همان جهت است. به عنوان مثال زمانی که ρ و g را ثابت در نظر بگیریم و شتاب در راستای x و y صفر باشد، می‌توان نوشت:

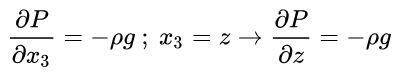
در نتیجه، می‌توان اختلاف فشار در دو نقطه از سیال را با انتگرال‌گیری از معادله بالا و به صورت زیر محاسبه نمود:

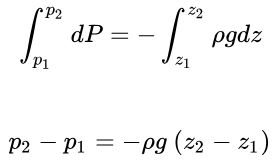
اگر نقطه p2 را در سطح در نظر بگیریم. با توجه به این که در این نقطه، فشار برابر با فشار اتمسفر است، می‌توان نوشت:

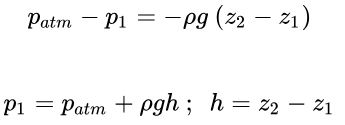
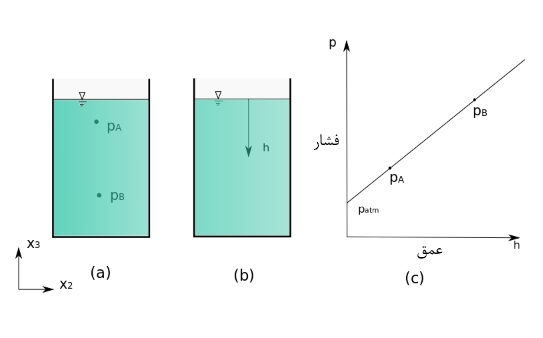
به این نکته توجه شود که h، فاصله از سطح سیال است. طبق معادله بالا و همان‌گونه که در شکل زیر نشان داده شده، اگر دو نقطه از سیال در یک ارتفاع باشند، قطعاً دارای فشار یکسانی خواهند بود؛ هم‌چنین می‌توان نتیجه گرفت که با افزایش ارتفاع و رفتن به عمق بیشتر، فشار سیال نیز زیاد‌تر خواهد شد. به همین دلیل، هنگام شنا کردن در عمق استخر فشار بیشتری روی پوست احساس می‌شود.

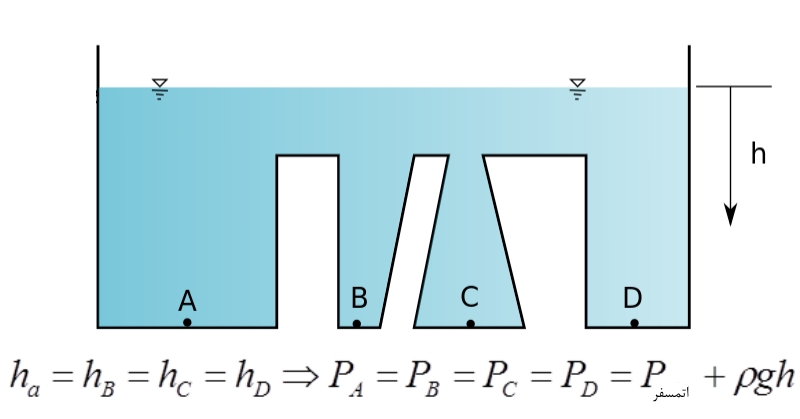
به عنوان مثال، شکل زیر را در نظر بگیرید و فرض کنید می‌خواهیم فشار سیال در نقطه C را محاسبه کنیم.

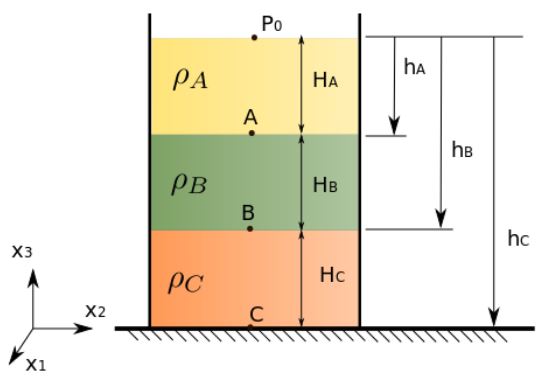
به منظور محاسبه فشار در این نقطه، به این ترتیب عمل خواهیم کرد:

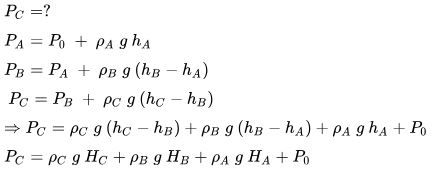
در مثال بالا به این نکته توجه کنید که جنس سیال‌های B ،A و C متفاوت هستند. در واقع اندازه فشار در یک نقطه از سیال فقط به فاصله آن از سطح آزاد و چگالی سیال وابسته است.

مکانیزم انتقال نیرو

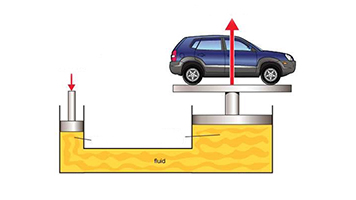
مایعات، تقریبا تراکم ناپذیر هستند. این ویژگی به ما کمک می‌کند تا بتوانیم از آن‌ها به منظور عامل انتقال نیرو استفاده کنیم. به عنوان مثال جک‌ هیدرولیکی، ابزاری است که از مفهوم تراکم ناپذیری سیالات بهره می‌برد. مکانیزم کارکرد چنین ابزارآلاتی نیز بر اساس مفاهیمی هستند که در بخش‌های قبل عنوان شدند.

فیلم آموزش مکانیک سیالات – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

لوله‌ای u شکل را در نظر بگیرید که توسط مایعی - مثل روغن - پر شده است. اگر دو نیرو به دو سمت این لوله به نحوی وارد شود که کل سیستم در حالت سکون باشد، می‌توان نوشت:

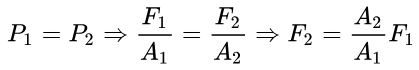
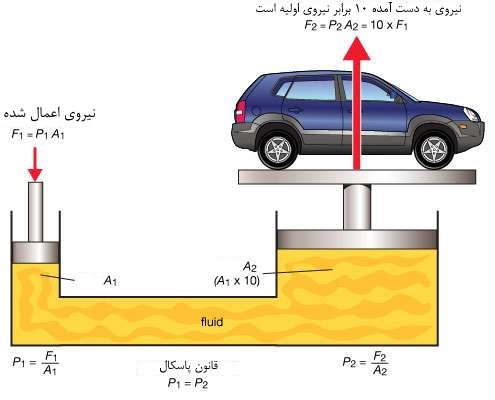
این رابطه نشان می‌دهد که اگر A2 بزرگ‌تر از A1 باشد، با اعمال نیروی F1 می‌توان به نیرویی بزرگ‌تر (F2)، در سمت دیگر لوله دست پیدا کرد. این قانونی است که پاسکال در سال 1647 عنوان کرد. همان‌گونه که در شکل زیر نشان داده شده، با اعمال نیرویی اندک در سمت چپ، می‌توان نیرویی ایجاد کرد که خودرو را به صورت معلق نگه می‌دارد.

در صورتیکه مطلب بالا برای شما مفید بوده است، احتمالاً آموزش‌های زیر نیز برایتان کاربردی خواهند بود.

• آموزش مکانیک سیالات
• آموزش ریاضیات مهندسی
• آموزش استاتیک
• آموزش ترمودینامیک

^^