اعداد توان دار — به زبان ساده (+ دانلود فیلم آموزش گام به گام)

در این مقاله قصد داریم تا با زبانی ساده، به اعداد توان دار در ریاضی بپردازیم و قواعد پیرامون آنها را مورد بررسی قرار دهیم. منظور از «توان» (Power or Index) در ریاضیات این است که یک عدد (پایه) به تعداد عدد توان در خودش ضرب میشود. در ادامه این مقاله از مجله فرادرس پس از ارائه مقدمات مورد نیاز، نحوه محاسبه توان به وسیله ماشینحساب و قواعد پایهای محاسبات توانی را بیان میکنیم.
فیلم آموزشی اعداد تواندار
اعداد توان دار در ریاضی
در مقاله «توضیح توان در ریاضیات — به زبان ساده» از مجله فرادرس با مقدمات و مفهوم توان در ریاضی آشنا شدید. در اینجا قصد داریم تا قواعد پایهای توان در ریاضی را مطرح کنیم.

به طور مثال، در تصویر فوق $$2^{3}$$ به این معنی است که عدد پایه (که در اینجا ۲ است) به تعداد عدد توان، یعنی ۳ مرتبه در خودش ضرب میشود. یعنی:
$$2^{3}=2\times2\times2=8$$
یا به طور مثال، در تصویر زیر، عدد ۳ به تعداد ۴ بار در خودش ضرب شده و حاصل آن 81 است.
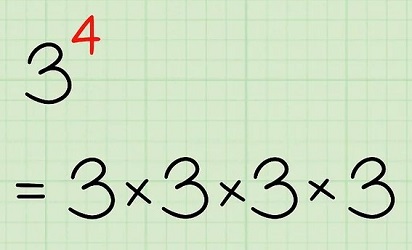
به عنوان مثالی دیگر، میخواهیم $$4^{5}$$ را حساب کنیم. در اینجا، پایه عدد ۴ و توان ۵ است. پس ۴ به توان ۵ یعنی، عدد ۴ را به تعداد ۵ مرتبه در خودش ضرب کنیم. به تصویر زیر دقت کنید.
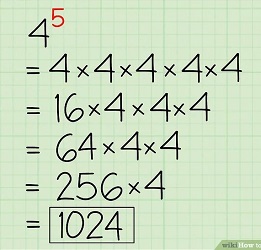
حال بیایید حاصل عبارت موجود در تصویر زیر را پیدا کنیم.

در اینجا ۳ به تعداد ۴ بار و ۲ به تعداد ۵ بار در خودشان ضرب میشوند. پس داریم:
$$3^{4}+2^{5}=3\times3\times3\times3+2\times2\times2\times2\times2=113$$
دقت کنید که پایه یک عبارت توانی به جز عدد، پارامتر هم میتواند باشد. به طور مثال در شکل زیر، پایه، پارامتر $$x$$ بوده و عبارت $$x^{3}$$ به معنی ضرب پارامتر $$x$$ به تعداد ۳ مرتبه در خودش است. حال به طور مثال اگر مقدار $$x$$ برابر با ۲ باشد، حاصل $$x^{3}=2^{3}$$ مقدار ۸ میشود.

محاسبه توان به کمک ماشین حساب
حال فرض کنید میخواهید عدد ۹ را به تعداد 15 بار در خودش ضرب کنید، در واقع هدف محاسبه ۹ به توان ۱۵ است. این کار به صورت دستی بسیار زمانبر خواهد بود. اما شما میتوانید به وسیله یک ماشینحساب در کسری از ثانیه این عمل را به راحتی انجام دهید. در اکثر ماشینحسابهای مهندسی، یا برنامههای ماشینحساب در محیط کامپیوتر یا تلفنهمراه، عمل محاسبه توان قابل انجام است. معمولاً در ماشین حسابها از علامت «^» یا «$$x^{y}$$» برای این کار استفاده میشود.
همچنین در برخی از ماشینحسابها عبارت EXP به این معنی است که عدد «نِپِر یا اویلر» به توان رسد. در واقع با فشردن دکمه EXP و وارد کردن عدد توان، عبارت $$e^{x}=2.71828^{x}$$ محاسبه میشود.

به عنوان مثال برای محاسبه $$9^{15}$$، ابتدا عدد ۹ را بفشارید و سپس با زدن دکمه «^» یا «$$x^{y}$$» مشاهده میکنید که عبارتی شبیه به $$9^{()}$$ نمایش داده میشود. حال با وارد کردن عدد ۱۵ و زدن مساوی نتیجه این عمل، نمایش داده میشود.

گاهی اوقات ماشینحسابها جواب را به صورت نماد علمی نمایش میدهند. یعنی یک عدد صحیح در چپ، اعشار، باقی ارقام ضرب در 10 به توان یک عدد میرسد. در تصویر فوق عدد 205,891,132,094,649 نمایش داده شده به صورت نماد علمی بوده که در آن $$E14$$ به معنی ۱۰ به توان ۱۴ است ($$E14=10^{14}$$). به بحث نماد علمی در انتهای مقاله بیشتر میپردازیم.
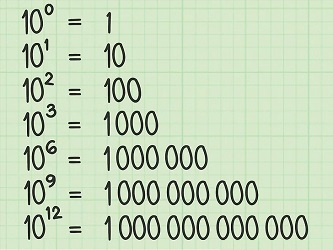
قوانین پایهای توان در ریاضی
برای سادگی حل مسائل دشوارتر و یا استفاده از اعداد توان دار در سایر علوم نیاز است که با قواعد آن آشنا شوید.
عدد به توان صفر
اگر هر عدد یا عبارتی جز صفر، به توانِ صفر برسد، آن را برابر با یک در نظر میگیریم. به عنوان مثال $$6^{0}=1$$ و $$9999^{0}=1$$ و $$z^{0}=1$$. عبارت $$0^{0}$$ (صفر به توان صفر) یا صفر به توان هر عدد برابر با صفر است. چرا که هیچچیزی وجود ندارد که بخواهد در خودش ضرب شود. واضح است که هر عدد به توانِ یک برابر با خودش است.
برای آشنایی بیشتر با این موضوع، به مطلب «هر عدد به توان صفر | صفر به توان هر عدد — به زبان ساده و با مثال» از مجله فرادرس مراجعه کنید.
عدد به توان بی نهایت
هر عددی به توان مثبت بینهایت، بینهایت شده و هر عددی به توان منفی بینهایت صفر میشود.
جمع اعداد توان دار
به هنگام جمع چند عدد توانی مشابه، میتوانیم یکی از عبارتها را نوشته و به تعداد عبارتها، ضریبی را برایش در نظر بگیریم. به طور مثال در تصویر زیر، عبارت $$4^{5}$$ با خودش جمع میشود. به جای محاسبه تک تک آنها و جمع کردن، میتوانیم $$4^{5}$$ را نوشته و عدد ۲ را به عنوان ضریب برایش در نظر بگیریم.
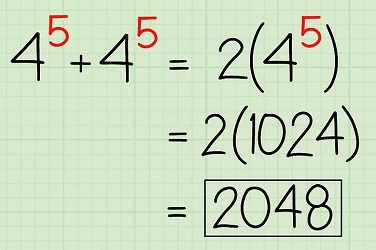
به عنوان مثالی دیگر میخواهیم عبارت $$4^{3}$$ را ۶ بار با خودش جمع کنیم. برای این کار به صورت زیر عمل میکنیم.
$$4^{3}+4^{3}+4^{3}+4^{3}+4^{3}+4^{3}=6\times4^{3}=384$$
ضرب اعداد توان دار
فرض کنید مطابق تصویر زیر، دو عبارت توانی در یکدیگر ضرب میشوند. در صورتی که پایهها یکسان باشند، میتوانیم پایه را نوشته و توانها را با یکدیگر جمع کنیم.
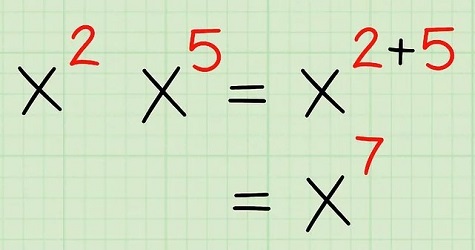
در تصویر فوق دو عبارت توانی $$x^{2}$$ و $$x^{5}$$ در یکدیگر ضرب میشوند. چون پایهها یکسان است ($$x$$) یک پایه را نوشته و سپس توانها را با یکدیگر جمع کردیم. به عنوان مثال دوم، به تصویر زیر دقت کنید:

توان در توان
اگر یک عبارت توانی، خودش به توان برسد، میتوانیم پایه را نوشته و سپس توانها را در یکدیگر ضرب کنیم. به عنوان مثال به تصویر زیر دقت کنید:

به عنوان مثالی دیگر حاصل عبارت $$(7^{4})^{3}$$ به صورت $$7^{12}$$ است.
تقسیم اعداد توان دار
در تصویر زیر دو عبارت $$m^{8}$$ و $$m^{2}$$ بر هم تقسیم شدهاند. اگر در تقسیم دو عبارت توانی بر یک دیگر، پایهها یکسان باشند، میتوانیم یک پایه را نوشته و توانها را از یکدیگر کم کنیم.

به عنوان مثالی دیگر به تصویر زیر دقت کنید. از آنجا که پایه دو عبارت یکسان نیست، برای راحتی کار، با نوشتن عدد ۴ به صورت $$2^{2}$$، پایهها را یکسان کرده تا بتوانیم از قاعده فوق استفاده کنیم.
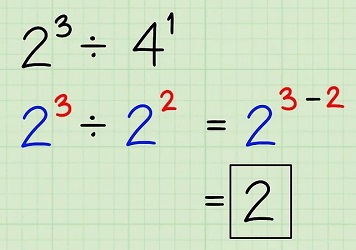
تصویر زیر نیز مثالی دیگر از قاعده گفته شد است. دقت شود که توان $$y$$ صفر شده و در نتیجه برابر با یک میشود.

توان منفی
اگر عددی به توان منفی برسد، به این معنی است که باید معکوس آن عبارت با توان مثبت را محاسبه کنیم. به عنوان مثال به تصویر زیر دقت کنید.
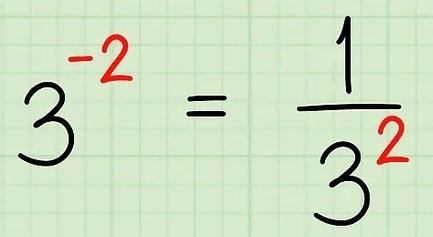
به عنوان مثالی دیگر به دو عبارات زیر توجه کنید:
$$x^{-1}=\frac{1}{x}$$
$$4^{-2}\times 8^{2}=\frac{8^{2}}{4^{2}}=\frac{64}{16}=4$$
مثال: به تصویر زیر دقت کنید.
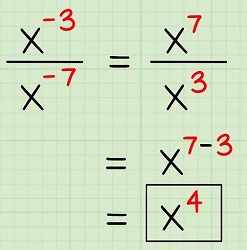
نماد علمی
یکی از کاربردهای توان در ریاضی استفاده از فرمت نوشتاری نماد علمی است. در علوم محاسباتی عموماً اعداد را به صورت نماد علمی مینویسند. این کار برای خلاصه نویسی و استفاده از پیشوندهای کاهنده (میلی، میکرو، نانو و ...) و یا افزاینده (کیلو، مگا، گیگا و ...) انجام میگیرد. به جدول پیشوندها در زیر دقت کنید:

به مثال تصویر زیر دقت کنید. میخواهیم عدد 93850000 را به صورت عددی (نماد) علمی بنویسیم. نمایش این عدد با استفاده از پیشوندها به صورت $$93.85\times 10^{6}=93.85M$$ در میآید.

همانطور که در تصویر فوق مشخص است، اگر نقطه اعشار را به سمت چپ حرکت دهیم از توان مثبت برای پایه 10 استفاده میکنیم و اگر نقطه اعشار را به سمت راست حرکت دهیم از توان منفی برای پایه ۱۰ استفاده خواهیم کرد. به طور مثال عدد 0.000006 به صورت نماد علمی و با استفاده از پیشوند میکرو به صورت زیر در میآید:
$$0.000006=6\times 10^{-6}=6\mu$$











سلام ببخشید اگر توان ها مساوی باشند اما پایه ها متفاوت برای ((جمع))توضیح دهید چگونه میشود؟ مثلا جمع ۳به توان ۲ با ۵به توان ۲
10 به توان x
به اضافه 10 به توان x
مساوی ۱۰ به توان ۴ شده یعنی x چند بوده ؟
۳ بوده
تعداد عداد عدد هایی که به توان بزرگ رسیدن رو چگونه پیدا کنیم
مثل دو به توان سیصد و سی و سه
جواب ۲ به توان ۲ به توان ۳۰ منهای ۱ چند میشه؟
1152921504606846976=60^2=30*2^(2)=30^(2^2)
نماد: ^=توان *=ضرب
ممنون
ممنون واقعا عالی بود با این استاد آدم راحت تر یاد میگیره??
واقعا حیفم اومد تشکر نکنم، ممنونم از شما.
جمع اعداد با توان مساوی ولی پایه های مختلف مثلا
1 به توان دو * 2 به توان دو الی اخر
فرمولی داره؟
سلام
A¹+A-¹
چطور حل کنم
سلام.
همانطور که میدانیم، $$ A^ {-1} = \frac 1 A $$ و $$A^1=A$$. بنابراین، عبارت را بهصورت $$A+\frac1A$$ است که اینگونه ساده میشود: $$A+\frac1A=\frac {A^2+1}{A}$$.
موفق باشید.
سلام.
آموزشهای «تصاعد هندسی و فرمول آن — به زبان ساده و با مثال» و «فرمول دنباله هندسی — به زبان ساده و با مثال» در این زمینه به شما کمک خواهند کرد.
سالم و موفق باشید.
اگر هم پایه ها وهم توان ها مساوی بود چی کنیم
باید یا از روش توان مساوی استفاده کنی یا از روش پایه مساوی
فقط از یکی از روش ها میتونی استفاده کنی
مرسی خوب بود✨♥️
یه سوال داشتم میخواستم بدونم اگر نه پایه و نه توان مساوی باشند حاصل هم مهمه که به دست بیاد باید چه کار کرد؟؟؟
مثلا:
۳^۲÷۲^۳
سلام تعداد رقمهای عدد ۳ به توان ۱۴۰۱ چند است
کسری بنویس نه بالا هشت پایین
توضیحات عالی
کسر ۹به توان منفی ۲ و۳ به توان۲ به صورت عدد توان دار بنویسید
میشه با جذر هم توضیح بدید؟
سلام ممنونم بابت آموزش خوبتون یه سوال داشتم. عدد دو به توان π چقدر میشه با دلیل لطفا برام توضیح بدید.ممنونم.
عدد منفی دو به توان دو مثبت چرا جوابش مثبت میشه؟؟
چون هر عدد منفی ضرب یه عدد منفی دیگه مثبت میشه و یه قانونه هر عدد منفی به توان دو جوابش مثبت میشه
سلام. بابت آموزش خوبتون ممنون.
ببخشید یه سوال؟
عدد ۵ به توان ۶ را گرفته به صورت ضرب دو عدد توان دار با پایه های مساوی بنویسید. اینو ایراد دارم میشه کمکم کنید
سلام و درود،
می توانید این عدد را به صورت حاصل ضرب دو مقدار ۵ به توان ۳ و ۵ به توان ۳ یا حتی ۵ به توان ۲ و ۵ به توان ۴ بنویسید. واضح است که هنگام ضرب دو عدد توان دار با پایه یکسان، نماها با یکدیگر جمع می شوند.
از اینکه مشکلاتتان را با ما درمیان می گذارید سپاسگزاریم.
تندرست و پاینده باشید.
با سلام
اگر در عبارتی مثلا ۲ به توان ۳ ضبدر ۲ به توان سه باشد(یعنی توان ها برابر و پایه ها هم )باید چه کرد؟
و اگر ۲ به توان ۳ به علاوه ۲به توان ۳ باشد باید چه کرد؟
باتشکر
اگر ۲ به توان ۳ + ۲به توان ۳ شد فقط کافی است
۲به توان ۳ را ×۲ بکنید ۲به توان ۳ ×۲ پایه ها برابر ۲ و توان ها جمع مساوی ۴ جواب میشه ۲به توان ۴
اگه داخل ضرب هم پایه وهم توانشون برابر باشه میتونی یا یک از پایه هارو بنویسی وتوان رو جمع کنی که میشه 2به توان شش یا پایه هارو ضرب کنی و یکی از توان هارو بنویسی که میشه 4به توان سه
سلام خسته نباشید
سه برابر عدد ۲۷به توان۳, چگونه محاسبه می شود
دوستی که این سوال رو پرسیدی 27 خودش سه ه توان 3 است یعنی 3 به توان 3 به توان 3 توان در توان هم توان ها در هم ضرب میشه پس 3 به 3 ضربدر 3 که میشه 3 به توان 9 ضربدر 3
3=3به توان 1 است پس برای ضرب دو عدد توان دار توان هارا جمع میکنیم که برابر سه به توان یک به علاوه نه میشه و جواب 3 به توان 10 است
سلام
اگر میشه بگید چگونه می توان اعداد معمولی را به اعداد توان دار تبدیل کرد؟؟
سلام. احتمالاً آموزش «تجزیه اعداد — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» به شما کمک خواهد کرد.
از همراهیتان با مجله فرادرس خوشحالیم.
خیلی خوب
عالی
خیلی ممنون از توضیحاتتون خیلی عالی
سلام
27 رو به توان سه برسونید
بعد حاصل رو ضرب در سه کنید.
سلام.bبتوان سه دوم مساوی 8 چه میشود؟
سلام خسته نباشید
سه برابر عدد ۲۷به توان۳, چگونه محاسبه می شود
سلام
یه سوال داشتم ، چجوری اعداد بین دو عدد توان دار رو پیدا کنیم ؟
مثلاً اعداد بین 3 به توان 19 و 3 به توان 20 رو چجوری پیدا کنیم ؟
سلام 27به توان3ضرب در ٣ می نویسیم. سپس ٢٧به توان ٣ را به ٣^(٣^٣)تبدیل می کنیم. پاسخ می شود 9^٣ضرب در 3 مساوی با 3به توان ده=10^3
ميشه سه به توان ۱۰
اعداد کوچکتر از یک و بزرگتر از منفی یک به توان بینهایت صفر می شود یا بینهایت
سلام
میخواستم بدونم هر عدد کسری به توان صفر هم برابر با یک است؟؟؟
با تشکر از سایت خوبتون
سلام.
طبق تعریف، هر عددی، شامل اعداد کسری، به توان صفر، برابر با یک است.
از همراهی شما سپاسگزاریم.
عالی