الگوهای عددی سخت — به زبان ساده و با مثال

با مجموعه اعداد طبیعی و همچنین اعداد حسابی آشنا هستید. اگر عضوی از اعضای این مجموعه به شما داده شود، میتوانید اعداد قبل یا بعد آن را تشخیص دهید. این موضوع نشان میدهد که در بین اعداد مجموعه اعداد طبیعی یا حسابی، الگوی عددی وجود دارد. به کمک این الگوهای عددی، میتوانیم اعضای مجموعه آنها را مشخص کنیم. در این متن با الگوهای عددی ساده آغاز کرده و با ذکر مثالهایی به الگوهای عددی سخت خواهیم رسید و اعضای مجموعه یا رابطه بین اعضای آنها را مشخص میکنیم. به این ترتیب آمادگی حل مسئلههای مربوط به الگویابی عددی را پیدا خواهید کرد.
بهتر است قبل از مطالعه این مطلب، در مورد مجموعهها و همچنین الگوها و دنبالههای حسابی اطلاعات بیشتری داشته باشید. پس پیشنهاد میکنیم که متنهای دیگر مجله فرادرس مانند مجموعه ها در ریاضیات – مفاهیم پایه و الگوها و دنباله های متداول عددی — به زبان ساده را بخوانید.
الگوهای عددی سخت
همانطور که میدانید، اعداد در شمارش و اندازهگیری به کار میروند. بخصوص اعداد طبیعی که در محیط ما برای شمارش اجسام و اشیاء مورد استفاده قرار میگیرد. مجموعه اعداد طبیعی، یک مجموعه از اعداد است که اغلب به صورت زیر نمایش داده میشود.
{ 1, 2, 3, ... }
معمولا این مجموعه را با حرف لاتین N نمایش میدهند.
اگر عضو صفر (۰) را هم به این مجموعه اضافه کنیم، مجموعه اعداد حسابی ساخته میشود.
{ 0, 1, 2, 3, ... }
این مجموعه نیز اغلب با حرف W شناخته میشود.

از قبل آموختهاید که مجموعه، یک دسته از عناصر یا اشیاء است که عضوهای آن را داخل علامتهای { } نوشته و با کاما (,) جدا میکنیم. در مجموعه، ترتیب قرار گرفتن عضوها مهم نیست. بنابراین مجموعه اعداد حسابی را به صورت زیر نیز میتوان نمایش داد.
{ 0, 3, 2, ۱, ... }
ولی در الگوها ترتیب قرارگیری هر یک از عضوها مهم است و باید زمانی که میخواهیم یک الگو را نمایش دهیم، ترتیب را رعایت کنیم. به همین جهت برای نمایش یک الگو یا دنباله، اعضای الگو را با کاما جدا کرده ولی از علامت { } استفاده نمیکنیم.
به این ترتیب الگو اعداد طبیعی یا حسابی را به شکل زیر به کار میبریم.
1, 2, 3, ... الگوی اعداد طبیعی
0, ۱, 2, 3, ... الگوی اعداد حسابی
الگوهای عددی چیست؟
همانطور که قبلا هم اشاره کردیم، در الگو و دنباله اعداد، ترتیب قرارگیری اعداد مهم است و این ترتیب به ما کمک میکند که با دانستن یک عدد، مقدار بعدی یا قبلی را مشخص کنیم.
برای مثال اگر الگوی اعداد طبیعی را در نظر گرفته باشیم، میتوانیم مقدار قبلی و بعدی عدد ۱۰ را مشخص کنیم. عدد ۹ مقدار قبلی و ۱۱ عدد بعدی در الگوی اعداد طبیعی برای ۱۰ هستند. ولی سوال اصلی این است که چگونه توانستیم چنین کاری را برای حدسی زدن مقدار قبلی یا بعدی در الگوی اعداد طبیعی انجام دهیم؟
طبق الگوی اعداد طبیعی، هر عدد با عدد بعدی خود یک واحد اختلاف دارد و از آن کوچکتر است. همچنین عدد انتخابی از عدد قبلی خود یک واحد بزرگتر است. همین رابطه بین اعداد به عنوان الگو معرفی میشود.
رابطه یا قاعده سازنده یک الگو را قانون الگو یا فرمول الگویابی میگوییم. در الگوهایی ساده به راحتی میتوان به مشاهده اعداد دنباله، قاعده را پیدا کرد. برای مثال الگو یا دنباله اعداد زوج به صورت زیر است. مشخص است که فاصله یا تفریق هر دو عدد زوج پشت سر هم، برابر با ۲ است. پس هر دو عدد متوالی در الگوی اعداد زوج، ۲ واحد با یکدیگر اختلاف دارند.
2, 4 ,6, 8, 10, 12, 14, ...
اولین عضو این الگو، ۲، عدد بعدی، ۴ و سپس ۸ و غیره است. توجه داشته باشید که علامت ... در انتهای این دنباله یا الگو، نشانگر آن است که این دنباله ادامه داشته و انتها یا پایان ندارد و به اصطلاح تا بینهایت ادامه دارد. رابطه بین دو عدد زوج که در کنار هم هستند در جدول زیر دیده میشود. به ستون «اختلاف با مقدار قبلی» توجه کنید.
جدول ۱: رابطه بین الگوی اعداد زوج
| شماره | عدد | اختلاف با مقدار قبلی |
| 1 | 2 | - |
| ۲ | ۴ | ۴ - ۲ = ۲ |
| ۳ | ۶ | ۶ - ۴ = ۲ |
| 4 | 8 | ۸ - ۶ = ۲ |
| 5 | 10 | 10 - 8 = 2 |
| ... | ... | ... |
میبینید که هر عدد با عدد بعدی خود ۲ واحد اختلاف دارد. از طرفی هر عدد از عدد قبلی خود هم بزرگتر است. چنین الگویی را یک دنباله یا الگوی ساده میگوییم. ولی در الگوهای عددی سخت رابطه بین مقدارها پیچیده و معمولا به کمک ضرب و جمع یا تقسیم و تفریق انجام میشود. در ادامه متن به الگوهای عددی ساده و سخت اشاره میکنیم و با روشهای ساختن آنها آشنا میشویم.
نکته: برای سطر شماره ۱، در ستون اختلاف با مقدار قبلی، علامت « - » گذاشتهایم زیرا مقدار قبلی برای شماره ۱ وجود ندارد تا اختلاف را اندازهگیری کنیم.
الگوهای عددی ساده کدامند؟
برای نمایش الگوهای عددی، دو راه وجود دارد. یا دنباله یا اعداد الگو را در کنار یکدیگر به ترتیب مینویسند یا قانون و رابطه الگو را مشخص میکنند. در ادامه هر دو کار را برای الگوهای عدد ساده به کار میبریم.
نمایش الگوهای عددی ساده با معرفی اعداد
ابتدا جدول ۱ را در نظر میگیریم تا به کمک اعداد الگوی زوج، قاعده یا رابطه بین اعداد آن را پیدا کنیم. میدانیم اولین مقدار (شماره ۱) در این الگو، عدد ۲ است. جدول ۲، رابطه این اعداد را با شماره ردیف جدول (شماره عضو الگو) مشخص کرده است.
جدول ۲: رابطه بین الگوی اعداد زوج
| شماره | رابطه |
| 1 | ۲ × ۱ = ۲ |
| ۲ | ۴ = ۲ × ۲ |
| ۳ | ۶ = ۳ × ۲ |
| ۴ | ۸ = ۴ × ۲ |
| ۵ | ۱۰ = ۵ × ۲ |
| ... | ... |
همانطور که میبینید، هر شماره در عدد ثابت ۲ ضرب شده و مقداری از اعداد الگو یا دنباله را تشکیل داده است. به این ترتیب الگو را به صورت زیر نشان میدهیم.
۲ × شماره = عدد الگو
بهتر است این موضوع را با شکل و نمایش تصویر، دنبال کنیم و الگوی عددی دیگری را مشخص کنیم. تعداد مربعهای هر یک از شکلها را بشمارید. به نظر شما چه رابطهای بین تعداد دایرههای شکلها وجود دارد؟
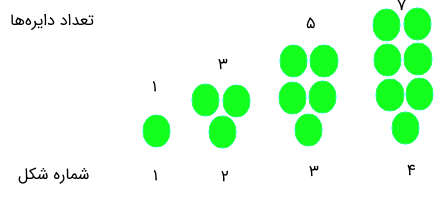
همانطور که دیده میشود، در شکل (۱)، یک دایره و در شکل (۲)، سه و در شکل (۳) پنج دایره و در شکل (۴) هم هفت دایره قرار دارد. اگر همین الگو را ادامه دهیم و به سمت راست و چپ هر شکل، تعداد دایرهها را دوبرابر کنیم و به آن یک دایره اضافه کنیم، شکل جدیدی ساخته شده که تعداد دایرههای آن از شکل قبلی ۲ واحد بیشتر است. پس با شمارش تعداد دایرهها به یک الگوی عدد ساده به صورت زیر میرسیم.
1, 3, 5, 7, 9, 11, 13, ...
الگوی ساخته شده درست به مانند الگو یا مجموعه اعداد فرد است. در این الگو به مانند الگوی اعداد زوج، هر عدد دو واحد از عدد قبلی خود بزرگتر است ولی با الگوی اعداد زوج این تفاوت را دارد که مقدار اول در این الگو عدد ۱ است. بنابراین الگو را به صورت زیر مینویسیم. توجه داشته باشید که شماره شکلها نیز از یک شروع میشوند.
1 - ۲ × شماره = عدد الگو
نمایش الگوهای عدد ساده با معرفی قانون یا رابطه
برای مشخص کردن یک الگو از اعداد، بهتر است دو موضوع را مشخص کنیم. مقدار اولین عدد در الگو و سپس قانون یا رابطه بین اعداد الگو باید معرفی و تعیین شوند. طبق الگوی اعداد فرد و و مقدار اول ۱، میتوانیم اعداد این دنباله را بسازیم. به یاد دارید که الگوی اعداد فرد به صورت زیر است.
1, 3, 5, 7, 9, 11, 13, ...
که میتوانیم آن را به وسیله شکلی مانند زیر معرفی کنیم.
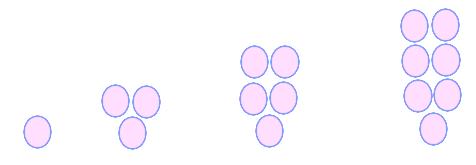
واضح است که میتوانیم این بار الگویی که به وسیله رابطه «1 + ۲ × شماره = عدد الگو» معرفی میشود را برای شکل بالا به کار ببریم. خانههای جدول زیر را به کمک این الگو پر میکنیم. در اینجا شماره را از صفر آغاز میکنیم. این الگو را با الگوی قبلی برای اعداد فرد مقایسه کنید. نتیجه یکسان است ولی فرمول الگویابی تفاوت دارد. زیرا نقطه شروع یا شماره را صفر در نظر گرفتهایم.
| شماره | عدد فرد | شماره | عدد فرد |
| ۰ | 1 | 4 | 9 |
| 1 | 3 | 5 | 11 |
| 2 | 5 | 6 | 13 |
| 3 | 7 | 7 | 15 |
الگوهای عددی سخت کدامند؟
شاید حدس زدن و پیدا کردن رابطه در الگوهای عددی سخت به سادگی و با یک عمل ضرب یا جمع صورت نگیرد. در این الگوها باید دقت بیشتری کرد تا رابطه بین عددها به درستی تعیین شود. این الگوها را هم بوسیله معرفی اعداد و هم رابطه مشخص میکنند. این دو روش در ادامه معرفی شدهاند.
نمایش الگوهای عددی سخت با معرفی اعداد
یک الگوی عددی به صورت زیر را در نظر بگیرید. هر چند این اعداد مربوط به اعداد طبیعی هستند ولی نمیتوانیم الگوی سادهای را برایشان مشخص کنیم.
1, 3, 6, 10, ...
چهار عدد اول این الگو را مشاهده میکنید. به نظر شما عدد پنجم در این الگو چیست؟ اختلاف عدد با عددی قبلی در این الگو به شکل زیر است.
3 - 1 = 2,
6 - 3 = 3,
10 - 6 = 4,
...
همانطور که میبینید مقدار اختلاف بین دو عضو کنار هم این دنباله، ثابت نیست. در چنین حالتهایی، با الگوهای عددی سخت مواجه هستیم. شماره عدد در الگو و مقدار آن را در جدول زیر قرار دادهایم.
جدول ۳: رابطه بین اعداد و اختلاف بین دو عدد در الگوی اعداد سخت
| شماره | اعداد | اختلاف با مقدار قبلی |
| 1 | 1 | - |
| 2 | 3 | 2 |
| 3 | 6 | 3 |
| 4 | 10 | 4 |
| ... | ... | ... |
برای بدست آوردن الگو یا رابطه بین اعداد دنباله یک رابطه به شکل زیر را به کار میبریم.
عدد الگو - عدد قبلی الگو = شماره
پس میتوانیم هر عدد این دنباله را با جمع کردن عدد قبلی با شماره مربوط به آن عدد در دنباله، بدست آوریم. برای مثال اگر قرار باشد، عدد پنجم این دنباله را محاسبه کنیم و بدانیم که عدد قبلی، ۱۰ است، خواهیم داشت.
عدد قبلی الگو + شماره = عدد الگو
10 + 5 = 15
همچنین عدد ششم هم به شکل زیر معرفی میشود.
21 = ۶ + 15
پس دنباله به شکلی که در ادامه خواهید دید، ادامه خواهد داشت.
1, 3, 6, 10, 15, 21, 28, ...
همانطور که دیدید، در این دنباله علاوه بر استفاده از شماره هر عدد در دنباله، از مقدار قبلی در دنباله هم استفاده کردیم. پس هر مقدار از این دنباله نه تنها به شماره محل قرارگیری آن در الگو ارتباط دارد بلکه به مقدار قبل در الگو هم مرتبط است. پس اگر قرار باشد مثلا مقدار ۲۰ام را در این دنباله مشخص کنیم، باید تا مقدار ۱۹ تعیین شده باشد، تا این کار قابل انجام باشد.
الگوی گفته شده را میتوان یک الگوی مثلثی نامید زیرا به کمک تعداد نقطههایی که در این اعداد مشخص میشود، مثلثهای همنهشت یا مشابه میتوان ساخت. به تصویر زیر دقت کنید. تعداد نقطه درون هر مثلث با اعداد الگوی مثلثی یکسان است.
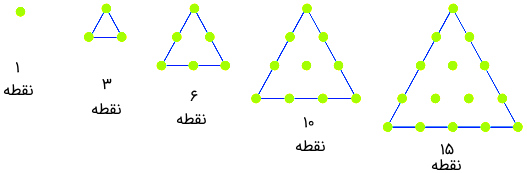
حال فرض کنید که با مثلث ۱۰ نقطهای سروکار داریم. این مثلث را میتوان به مثلثهایی با سه نقطه تبدیل کرد. به تصویر زیر نگاه کنید.
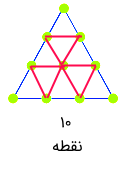
همچنین الگوی اعدادی مربعی نیز به شکل زیر داریم. هر کدام از این اعداد به صورت حاصلضرب یک عدد در خودش بوجود آمدهاند. برای مثال، عدد اول، از حاصل ضرب شماره ۱ در خودش ساخته شده که مشخص است برابر با ۱ خواهد شد. همچنین عدد شماره ۲ نیز از ضرب ۲ در ۲ ساخته شده و مقدار آن ۴ است. عدد سوم هم از ضرب ۳ در ۳ برابر با ۹ و عدد چهارم هم از ضرب ۴ در خودش بدست میآید.
1, 4, 9, 16, 25, 36, ...
میتوانیم این اعداد را به صورت مربعهایی نمایش دهیم که مساحت این مربعها با عدد دنباله برابر است. به تصویر زیر توجه کنید. الگوهای عددی سخت معمولا به صورتی ترکیب ضربها نوشته میشوند.
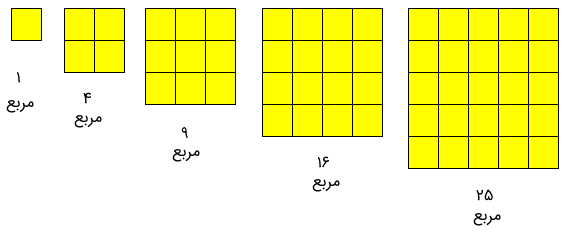
در ادامه فرمول مربوط به الگوی مثلثی و مربعی را مشخص میکنیم.
مسئله: به نظر شما اعداد بعدی برای الگوی زیر کدام است؟
2, 5, 10, 17, ___ , ____
راه حل: اول شماره و اعداد در دنباله را در کنار هم دیگر قرار میدهیم.
| 1 | 2 | 3 | 4 |
| 2 | 5 | 10 | 17 |
ردیف اول در جدول، شماره و ردیف دوم، عدد دنباله را مشخص کرده. اختلاف دو عدد اول و دوم برابر با ۳ ولی اختلاف دو عدد دوم و سوم برابر با ۵ و همچنین اختلاف دو عدد سوم و چهارم هم برابر با ۷ است. پس چون اختلافها ثابت نیست، الگو باید شامل یک ضرب باشد.
حاصل ضرب شماره در خودش به مقدار عدد الگو نزدیک است. برای مثال حاصل ضرب شماره ۳ در خودش برابر با ۹ است که با مقدار ۱۰ یک واحد اختلاف دارد. همچنین حاصلضرب شماره ۴ در خودش برابر با ۱۶ است که با عدد الگو یعنی ۱۷، یک واحد فاصله دارد. پس شاید رابطه زیر برای الگو مناسب باشد.
۱ + (شماره × شماره) = عدد الگو
برای امتحان هم برای شماره ۱ و ۴ این کار را انجام میدهیم.
2 = (۱ × ۱) + 1
۱۷ = (۴ × ۴) + 1
پس رابطه الگو را به درستی معرفی کردهایم، هر چند که این اعداد یکی از الگوهای عددی سخت محسوب میشود.
نمایش الگوهای عددی با معرفی قانون یا رابطه
این بار یک قانون برای رابطه بین اعداد الگو را معرفی میکنیم و با تعیین مقدار اول برای آن، بقیه اعضای دنباله عددی را میسازیم. فرض کنید که رابطه به صورت زیر باشد.
شماره × شماره = عدد الگو
به این ترتیب اگر اولین شماره این الگو، ۱ باشد، بقیه طبق جدول ۳ با الگوی گفته شده، محاسبه میشوند.
جدول ۴: رابطه بین اعداد و اختلاف بین دو عدد در الگوی اعداد مربعی
| شماره | عدد | اختلاف |
| 1 | 1 | - |
| 2 | 4 | 3 |
| 3 | 9 | 5 |
| 4 | 16 | 7 |
| 5 | 25 | 9 |
| ... | ... | ... |
همانطور که میبینید، این الگوی عددی سخت است زیرا فاصله بین مقدارهای آن ثابت نیست. به همین جهت معمولا رابطه به صورت ضرب یا تواندار کردن نوشته میشود.
به نظر شما الگوی اعداد زیر چه دنبالهای خواهد ساخت؟ البته اولین شماره نیز از ۱ آغاز میشود.
((شماره + ۱) × شماره ) ÷ ۲
اگر به شماره «شماره» مقدار ۱ قرار دهیم، حاصل برابر با ۲/(۱×۲) است که حاصل همان ۱ است. پس عدد اول دنباله برابر با ۱ است. با قرار دادن ۲ به جای شماره، مقدار به صورت ۲/(۳×۲) = ۳ بدست میآید. پس دومین عدد این دنباله، ۳ است. به همین ترتیب برای سومین (۲/ (۳×۴) = ۶) و چهارمین (۲/(۴×۵) = ۱۰) هم بدست میآید. پس دنباله یا الگوی اعداد به صورت زیر خواهد بود.
1, 3, 6, 10, ...
این الگو را در قسمت قبلی نیز به کار بردیم ولی الگویی که برای آن در آن قسمت نوشتیم با الگوی جدید تفاوت دارد. این موضوع نشان میدهد که برای یک دنباله از اعداد ممکن است الگوهای متفاوتی ایجاد شود که همگی یک دنباله را ایجاد کنند.

از همین شیوه هم میتوان برای نمایش الگوی اعداد مکعبی استفاده کرد. اگر الگوی محاسبه را به صورت ضرب سه بار مقدار شماره در خودش در نظر بگیریم، یک الگوی مکعبی ساختهایم. جدول زیر به الگوهای عددی سخت به شکل مکعبی مربوط است. رابطه بین اعداد آن را با دقت میتوان بدست آورد. توجه دارید که عدد اول را هم همان شماره در نظر گرفتهایم.
جدول ۵: رابطه بین اعداد و اختلاف بین دو عدد در الگوی اعداد سخت
| شماره | عدد | اختلاف |
| 1 | 1 | - |
| 2 | ۸ | 7 |
| 3 | ۲۷ | 19 |
| 4 | 64 | 37 |
| 5 | 125 | 61 |
| 6 | 216 | 91 |
| 7 | 343 | 127 |
| ... | ... | ... |
همانطور که میبینید اختلاف بین دو مقدار متوالی، به سرعت زیاد میشود. این الگو را به کمک مکعبها نمایش میدهند که لازم است تصویرها را به صورت سه بعدی بکشیم از نمایش آن صرفه نظر کردهایم.
کاربردهای الگوهای اعداد
دنباله یا الگوهای عددی متفاوت و همچنین پیچیدهای در ریاضیات وجود دارد که در طبیعت نیز کاربرد دارند. برای مثال دنباله یا سری فیبوناچی در بورس، نقاشی و عکاسی مورد استفاده قرار میگیرد. این دنباله به شکل زیر نوشته میشود.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ...
همانطور که میبینید، دنباله فیبوناچی، با صفر و یک شروع میشود، با جمع کردن دو عدد قبلی، یک عدد دیگر از این دنباله بدست میآید.
تصاعد حسابی یا دنباله حسابی نیز یک الگوی عددی را نشان میدهد که در آن هر عدد با جمع کردن عدد قبلی با یک مقدار مشخص و ثابت محاسبه میشود. فرض کنید که عدد اول الگوی حسابی ۰ و میزان افزایش هم ۳ باشد. به این ترتیب با توجه به الگوی حسابی (اضافه کردن یک عدد)، دنباله یا الگوی عددی حسابی به شکل زیر نوشته میشود.
۰, 3, 6, 9, 12, ...
جالب است که در اینجا اختلاف بین هر دو عدد دنبال هم، ثبات و برابر با ۳ خواهد بود.
دنباله هندسی نیز نوع دیگری از الگوهای اعداد را مشخص میکند که در آن هر عدد به وسیله ضرب آن در یک عدد ثابت در عدد قبلی بدست میآید. در ادامه یک دنباله یا الگوی هندسی را مشاهده میکنید که با مقدار 1 آغاز شده و مضرب مورد نظر، ۲ است.
۱, 2, 4, 8, 16, 32, 64, 128, 256, …
همانطور که میبینید، تقسیم دو عدد پشت سر هم در این دنباله، برابر با ۲ است. مثلا ۳۲ تقسیم بر ۱۶ برابر با ۲ و همچنین ۲۵۶ تقسیم بر ۱۲۸ نیز خارج قسمتی برابر با ۲ دارد. عدد ۲ در اینجا همان مضرب مورد نظر در دنباله هندسی است.
در ریاضی، دنبالههای بسیار زیادی وجود دارند و حتی شما هم میتوانید با معرفی یک رابطه بین اعداد و مشخص کردن اولین عدد، یک دنباله بسازید. البته مهم است که دنبالهای که ساختهاید به چه کاری میآید و کاربرد آن در کجاست. دانشمندان و ریاضیدانها از دنبالههای عددی برای پیدا کردن رفتار الگوهای عددی استفاده میکنند تا بتوانند مقدار پدیدههایی که با این الگو همساز هستند را تشخیص داده و آینده را پیشبینی کنند.
خلاصه و جمعبندی
تشخیص الگوی اعداد و ساختن دنبالهای از اعضای آن ممکن است کار مشکلی باشد. ولی در این متن به معرفی چند الگوی مشخص پرداختیم و با استفاده از مثالهایی، کم کم الگوهای عددی سخت و پیچیده را ساختیم. همانطور که دیدید، در بیشتر موارد، الگوها بوسیله عمل جمع ساخته میشود ولی ممکن است این جمع تبدیل به ضرب شده و باعث ایجاد الگوهای عددی سخت شود. در این متن به هر دو گونه الگوهای عددی یعنی الگوهای ساده و سخت پرداختیم و به کمک معرفی اعداد الگو یا ساختن رابطه بین اعداد، الگوها را شناختیم.












