فیلتر میان نگذر چیست؟ — از صفر تا صد

در مطلب قبلی از مجله فرادرس به بررسی انواع مختلف فیلترها مانند فیلتر پایین گذر اکتیو، فیلتر بالا گذر اکتیو، فیلتر میان گذر اکتیو، فیلتر بالا گذر پسیو و فیلتر پایین گذر پسیو پرداختیم. در این مطلب قصد داریم به بررسی یک نوع دیگر از فیلترها بپردازیم که به آن «فیلتر میان نگذر» (Band Stop Filter) میگویند. البته این نوع فیلتر را گاهی با نام «فیلتر شکافی» (Notch Filter) نیز میشناسند. یک فیلتر میان نگذر یا یک فیلتر شکافی فرکانسهایی را مسدود و حذف میکند که در بازه بین دو فرکانس نقطه قطع فیلتر قرار دارند، در حالی که سایر فرکانسهای موجود در دو طرف خارج از این باند را عبور میدهند.
فیلتر میان نگذر
از طریق ترکیب کردن یک فیلتر پایین گذر RC ساده با یک فیلتر بالا گذر RC میتوانیم به سادگی یک فیلتر میان گذر را ایجاد کنیم که اجازه عبور فرکانسهای موجود در بازه بین دو فرکانس قطع را میدهد. اما این امکان نیز وجود دارد که همان فیلترهای بالا گذر و پایین گذر را به نحوی دیگر به هم متصل کنیم که یک نوع پیکربندی متفاوت با شبکههای فیلتر RC به وجود بیاید. به این پیکر بندی فیلتر میان نگذر میگویند. همان طور که اشاره کردیم، در یک فیلتر میان نگذر، باند فرکانسی موجود در بین دو فرکانس قطع یا کامل حذف میشود و یا تا حد بسیار زیادی تضعیف میشود.
فیلتر میان نگذر که به اختصار به آن BSF نیز میگویند، در واقع یک نوع از مدارات «انتخابگر فرکانس» (Frequency Selective) است که عملکرد آن ها دقیقا برعکس عملکرد یک فیلتر میان گذر است که قبلا بررسی کردیم. یک فیلتر میان نگذر که به آن فیلتر حذف باند نیز میگویند، تمام فرکانسها، به غیر از فرکانسهای بازه توقف را از خود عبور میدهد. فرکانسهای موجود در یک باند توقف مشخص در این فیلتر به شدت تضعیف میشوند.
اگر این باند توقف بسیار باریک باشد و در بازهای چند هرتزی، تضعیف بسیار شدیدی صورت گیرد، آنگاه به فیلتر میان گذر عموما فیلتر شکافی میگویند؛ زیرا پاسخ فرکانسی این فیلتر، شکافی عمیق همراه با قدرت گزینشگری بسیار بالا (یک منحنی پله مانند با شیب تند) را نشان میدهد، در حالی که نمودار پاسخ فرکانسی سایر فیلترهای میان نگذر دارای یک باند وسیعتر و تغییرات هموارتر است. درست همانند یک فیلتر میان گذر، فیلتر میان نگذر (یا فیلتر شکافی یا حذف باند) یک مدار فیلتر مرتبه دو است که دو فرکانس قطع دارد. به این فرکانسهای قطع عموما فرکانس یا «نقاط نیم توان» (Half-Power Points) میگویند. فیلتر میان نگذر یک باند توقف فرکانسی را بین دو فرکانس قطع به وجود میآورد.
بنابراین عملکرد یک فیلتر میان نگذر به این صورت است که فرکانسهای از صفر (مقدار DC) تا اولین یا پایینترین نقطه فرکانس قطع، یعنی و نیز تمام فرکانسهای بالاتر از دومین یا بزرگترین فرکانس قطع، یعنی را عبور میدهد، اما فرکانسهای بین این دو نقطه را یا کاملا رد و یا تضعیف میکند. بنابراین میتوان گفت پهنای باند فیلتر یا BW بر اساس به دست میآید. بنابراین در یک فیلتر میان نگذر «پهن باند» (Wide Band)، باند توقف واقعی فیلتر بین دو نقطه پایین و بالا است که فرکانسها در این بازه حذف میشوند. بر همین اساس منحنی پاسخ فرکانسی مربوط به یک فیلتر میان نگذر ایدهآل را میتوان همانند تصویر زیر در نظر گرفت.
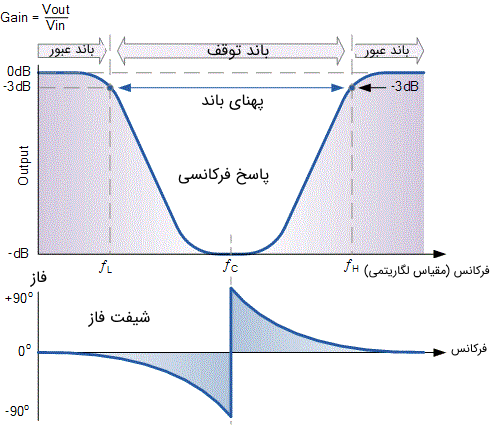
در نمودارهای دامنه و فاز مربوط به فیلتر میان نگذر که در تصویر فوق نشان داده شده اند، میتوان به راحتی مشاهده کرد که مقادیر و و بسیار مشابه با همان نقاطی هستند که برای توصیف رفتار یک فیلتر میان گذر از آنها استفاده کردیم. این امر بدین دلیل است که فیلتر میان نگذر در واقع فرم مکمل یا معکوس شده فیلتر میان گذر استاندارد است.
تعاریفی که برای پهنای باند، باند عبور، باند توقف و فرکانس مرکزی ارائه میشوند، همانند قبل هستند و ما میتوانیم از فرمولهای مشابهی برای محاسبه پهنای باند BW، فرکانس مرکزی و فاکتور کیفیت Q استفاده کنیم. فیلتر میان نگذر ایدهآل در باند توقف خود دارای تضعیف بینهایت است، در حالی که در هر دو باند عبور تضعیف آن صفر در نظر گرفته میشود. همچنین گذار بین هر دو باند عبور و باند توقف به صورت عمودی (شکل پله) است.
پیکربندی فیلترهای میان نگذر معمولی
راههای مختلفی برای طراحی یک فیلتر میان نگذر وجود دارد، اما همه این روشها در نهایت نتیجه یکسانی را خواهند داشت. در حالت کلی یک فیلتر میان گذر با استفاده از ترکیب یک فیلتر پایین گذر یا LPF به صورت سری با یک فیلتر بالا گذر یا HPF ساخته میشود. اما فیلترهای میان نگذر از ترکیب فیلتر بالا گذر و فیلتر پایین گذر در پیکربندی موازی ایجاد میشوند.
در تصویر زیر نمایی از یک پیکربندی معمولی برای فیلتر میان نگذر نشان داده شده است.
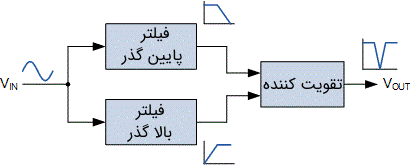
توجه کنید که در یک فیلتر میان نگذر، جمع کردن یک فیلتر پایین گذر با یک فیلتر بالا گذر به این معنی است که بر خلاف فیلتر میان گذر، پاسخ فرکانسی آنها نباید با یکدیگر «همپوشانی» (Overlap) داشته باشد. این مشخصه به دلیل این واقعیت است که فرکانسهای شروع و پایان این دو فیلتر در دو نقطه فرکانسی متمایز از یکدیگر قرار گرفته است. به عنوان مثال فرض کنید یک فیلتر پایین گذر مرتبه اول با فرکانس قطع را به صورت موازی به یک فیلتر بالا گذر مرتبه اول با فرکانس قطع متصل کنیم. به دلیل این که این دو فیلتر به صورت موازی به همدیگر متصل شدهاند، در نتیجه همانند شکل فوق، سیگنال ورودی به صورت همزمان به هر دو فیلتر اعمال میشود.
تمام فرکانسهای ورودی که زیر ۲۰۰ هرتز باشند، توسط فیلتر پایین گذر و بدون هیچ تضعیفی به سمت خروجی عبور داده میشوند. به طریق مشابه، تمام فرکانسهای ورودی بزرگتر از ۸۰۰ هرتز توسط فیلتر بالا گذر بدون تضعیف در خروجی قابل دریافت هستند. با این حال، تمام فرکانسهای ورودی بین این دو فرکانس قطع ۲۰۰ هرتز و ۸۰۰ هرتز (فرکانس قطع پایین و فرکانس قطع بالا) توسط هر دو فیلتر حذف میشوند و یک شکاف در پاسخ خروجی فیلتر به وجود می آید.
به عبارت دیگر، یک سیگنال با فرکانس کوچکتر از ۲۰۰ هرتز یا بزرگتر از ۸۰۰ هرتز به سادگی و بدون هیچ تغییری از فیلتر عبور میکند، اما یک سیگنال با فرکانس فرضا ۵۰۰ هرتز توسط فیلتر مسدود میشود؛ زیرا این فرکانس برای عبور از فیلتر پایین گذر بسیار کوچک است و از طرف دیگر برای عبور از فیلتر بالا گذر نیز بسیار بزرگ محسوب میشود. تاثیر این مشخصه فرکانسی در نمودارهای تصویر زیر نشان داده شده است.
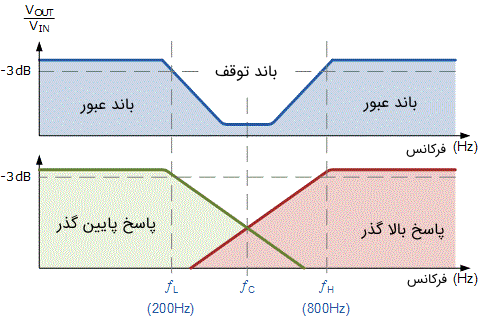
مدار فیلتر میان نگذر
مشخصه یک فیلتر میان نگذر را میتوان به سادگی با استفاده از یک مدار فیلتر بالا گذر و نیز یک فیلتر پایین گذر پیاده سازی کرد. البته این دو فیلتر باید توسط یک تعقیب کننده ولتاژ غیر معکوس کننده با بهره ولتاژ یک از یکدیگر ایزوله شوند. سپس خروجی این دو مدار فیلتر را باید با استفاده از یک تقویت کننده عملیاتی یا اپ امپ سوم با هم جمع کرد.
توجه کنید که تقویت کننده عملیاتی به عنوان جمع کننده ولتاژ متصل شده است. در تصویر زیر مدار یک فیلتر میان نگذر نشان داده شده است.
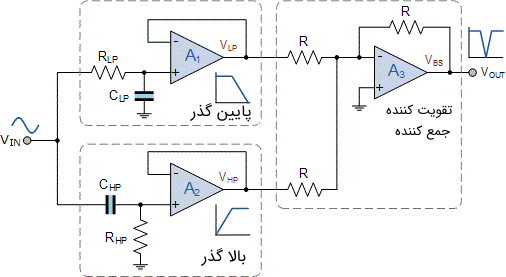
کاربرد تقویت کننده عملیاتی در طراحی یک فیلتر میان نگذر این امکان را به ما میدهد که یک بهره ولتاژ را نیز به مدار فیلتر پایه اضافه کنیم. دو تعقیب کننده ولتاژ غیر معکوس کننده را میتوان به راحتی به یک تقویت کننده پایه غیر معکوس کننده تبدیل کرد که دارای بهره ولتاژ باشد. برای این کار باید مقاومتهای فیدبک و ورودی را به مدار اضافه کرد. نحوه انجام این کار در مطلب تقویت کننده عملیاتی غیر معکوس کننده با جزئیات بیشتری توضیح داده شده است.
همچنین اگر به یک فیلتر میان نگذر نیاز داشته باشیم که نقاط فرکانس قطع آن فرضا در ۱ کیلو هرتز و ۱۰ کیلو هرتز قرار داشته باشند و همچنین بهره باند توقف میان این دو فرکانس برابر با باشد، آنگاه می توانیم به سادگی یک فیلتر پایین گذر و یک فیلتر بالا گذر را طراحی کنیم که این شروط را برآورده کنند. سپس باید آنها را با آرایش آبشاری به هم متصل کنیم تا فیلتر میان نگذر پهن باند مورد نظر ما به دست آید. حال که با اصول کاری یک فیلتر میان نگذر آشنا شدیم، قصد داریم در ادامه به طراحی یک فیلتر میان نگذر با فرکانسهای قطع پایین و بالا ۲۰۰ هرتز و ۸۰۰ هرتز بپردازیم.
مثال ۱: طراحی مدار فیلتر میان نگذر
یک فیلتر میان نگذر شبکه RC پهن باند را در نظر بگیرید که دارای فرکانس قطع پایین برابر با ۲۰۰ هرتز و فرکانس قطع بالای ۸۰۰ هرتز باشد. مقادیر فرکانس مرکزی، پهنای باند و فاکتور Q را محاسبه کنید.
حل:
مقادیر فرکانس قطع بالا و پایین برای یک فیلتر میان نگذر را میتوان با فرمول مشابه با فیلترهای بالا گذر و پایین گذر به دست آورد:
فرض میکنیم مقدار خازن C برای هر دو بخش فیلتر برابر با ۰٫۱ میکروفاراد باشد، در این حالت مقدار دو مقاومت تعیین کننده فرکانس، یعنی و به صورت زیر محاسبه میشوند. برای بخش فیلتر پایین گذر داریم:
همچنین مقاومت بخش بالا گذر به صورت زیر است:
حال با توجه به مقادیری که در بالا به دست آوردیم، مقدار فرکانس مرکزی از طریق رابطه میانگین هندسی به صورت زیر محاسبه میشود:
حال که مقادیر المانهای مربوط به دو طبقه فیلتر را به دست آوردیم، میتوانیم آنها را با یک مدار جمع کننده ولتاژ تکی ترکیب کنیم تا طراحی مدار کامل شود. دامنه (بزرگی) و پلاریته خروجی جمع کننده در هر لحظه از زمان برابر با جمع جبری دو ورودی آن است. توجه کنید که اگر مقدار مقاومت فیدبک اپ امپ و دو مقاومت ورودی آن را با یکدیگر برابر در نظر بگیریم، در آن صورت مدار جمع کننده معکوس کننده یک جمع صحیح ریاضی از دو سیگنال ورودی با بهره ولتاژ صفر ارائه میدهد. در نهایت مدار طراحی شده برای فیلتر میان نگذر با مقادیر فوق به صورت زیر است.
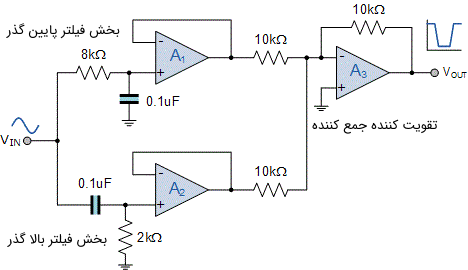
فیلتر شکافی
در مطالب فوق دیدیم که یک فیلتر میان نگذر ساده را میتوان با فیلترهای پایین گذر و بالا گذر مرتبه یک یا مرتبه دو همراه با یک مدار اپ امپ جمع کننده غیر معکوس کننده پیادهسازی کرد و باند وسیعی از فرکانسها را حذف کرد. همچنین میتوان یک فیلتر میان نگذر را به صورتی طراحی و اجرا کرد که پاسخ فرکانسی بسیار نازکتری داشته باشد. در این حالت، فرکانسهای خاصی حذف میشوند و به عبارت دیگر، قدرت گزینشگری فیلتر بالاتر میرود. به این نوع از فیلترهای میان نگذر، فیلتر شکافی میگویند.
بنابراین فیلترهای شکافی یک نوع از فیلترهای میان نگذر هستند که قدرت گزینشگری بسیار بالا و نیز Q بزرگی دارند و برای حذف کردن یک فرکانس منفرد و یا یک بازه بسیار نازک از فرکانسها، به جای یک بازه وسیع از فرکانسهای مختلف، مورد استفاده قرار میگیرد. به عنوان مثال، ممکن است لازم باشد که یک فرکانس مشخص که توسط نویز الکتریکی تولید میشود، تضعیف یا حذف شود. این فرکانسها معمولا توسط بارهای القایی مانند موتورهای الکتریکی و روشنایی بالاست و یا حذف هارمونیکها در مدار اصلی القا میشوند.
اما علاوه بر فیلتر کردن، یک فیلتر شکافی متغیر توسط موسیقیدانان در ادوات صوتی مانند «اکوالایزرهای گرافیکی» (Graphic Equalizers)، «ترکیب کنندهها» (Synthesizers) و «رکهای استودیویی» (Electronic Crossovers) مورد استفاده قرار میگیرد. هدف از به کارگیری یک فیلتر شکافی در این ابزارها این است که با پیکهای باریک موجود در پاسخ آکوستیک موسیقی برخورد شود. بنابراین میتوان دید که یک فیلتر شکافی در گستره وسیعی از کاربردها و مانند فیلترهای بالا گذر یا فیلترهای پایین گذر مورد استفاده قرار میگیرد.
فیلترهای شکافی در پاسخ، باند توقف بسیار باریک و نیز بسیار عمیقی حول فرکانس مرکزی خود دارند. پهنای شکاف در این فیلترها توسط فاکتور گزینشگری Q و دقیقا به روشی مشابه با پیکهای فرکانس رزونانس در مدارات RLC توصیف میشود. معروفترین طراحی فیلتر شکافی، شبکه فیلتر شکافی «T دوقلو» (Twin-T) است. پیکربندی شبکه T دوقلو که به آن T موازی نیز میگویند، در سادهترین فرم خود از دو شاخه RC به شکل دو حرف T تشکیل شده است. این مدار از سه خازن و سه مقاومت تشکیل شده است که مقادیر مقاومتها و خازنها در قسمتهای مختلف آن و نحوه اتصال آنها به یکدیگر در شکل زیر نشان داده شده است.
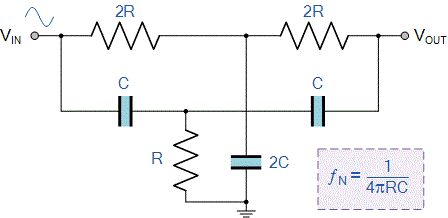
همان طور که در تصویر فوق نیز دیده میشود، حرف T بالایی در مدار از مقاومتهای 2R و خازن 2C تشکیل شده است که متعلق به قسمت فیلتر پایین گذر هستند، در حالی که قسمت T پایینی از مقاومت R و خازنهای C تشکیل شده است که به مدار فیلتر بالا گذر تعلق دارند. فرکانسی که در آن این طراحی ساده فیلتر شکافی T دوقلو بیشینه تضعیف را ارائه میدهد، «فرکانس شکاف» (Notch Frequency) نام دارد و با نماد نشان داده میشود. در یک فیلتر شکافی، فرکانس شکاف با معادله زیر به دست میآید:
فیلتر شکافی T دوقلو
به دلیل اینکه یک فیلتر شکافی T دوقلو ساده اساسا از یک شبکه RC پسیو تشکیل شده است، در نتیجه عیب بزرگ این مدار این است که بیشینه مقدار خروجی در مقادیر کمتر از فرکانس شکاف معمولا کمتر از مقدار بیشینه خروجی برای مقادیر بالاتر از فرکانس شکاف است. دلیل این امر این است که دو مقاومت سری 2R در بخش فیلتر پایین گذر، اتلاف بالاتری را نسبت به راکتانس دو خازن سری C در بخش فیلتر بالا گذر ایجاد میکنند.
علاوه بر بهره نابرابر در دو سمت فرکانس شکاف، عیب دیگری که در مدار فیلتر شکافی T دوقلو وجود دارد این است یک مقدار Q ثابت برابر با ۰٫۲۵ در حدود 12- دسیبل دارد. این امر بدین دلیل است که در فرکانس شکاف، راکتانس دو خازن سری برابر با رزیستانس دو مقاومت سری است و همین باعث میشود که جریانی که در هر کدام از شاخهها برقرار میشوند، به اندازه ۱۸۰ درجه با همدیگر اختلاف فاز داشته باشند.
این مدار فیلتر شکافی T دوقلو را میتوان بهبود داد و فیلتر شکافی را به وجود آورد که قدرت گزینشگری بالاتری داشته باشد. برای این کار میتوان از فیدبک مثبت متصل به مرکز دو شاخه اصلی استفاده کرد. به جای اتصال پیوند R و 2C به زمین، میتوان آن را به پین مرکزی شبکه مقسم ولتاژ متصل کرد که از سیگنال خروجی تغذیه میشود. مقدار فیدبک سیگنال که توسط نرخ مقسم ولتاژ تنظیم میشود، مقدار Q را مشخص میکند. Q نیز به نوبه خود، یک عامل تعیین کننده عمق شکاف در نظر گرفته میشود. مداری که در این حالت به وجود میآید، فیلتر شکافی T دوقلو تک اپ امپی نام دارد که در تصویر زیر نشان داده شده است.
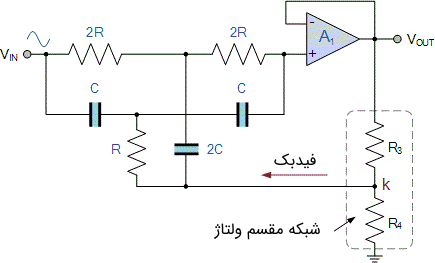
در مدار فیلتر شکافی T دوقلو تک اپ امپی، خروجی مدار توسط یک بافر اپ امپی غیر معکوس کننده تکی از مقسم ولتاژ ایزوله شده است. خروجی مدار مقسم ولتاژ به نقطه اتصال به زمین R و 2C متصل شده است. مقدار فیدبک سیگنال که به آن سهم فیدبک K میگویند، توسط نسبت مقاومتها تنظیم میشود و دارای رابطه زیر است:
مقدار Q بر اساس نسبت مقاومتهای و تعیین میشود، اما اگر بخواهیم فاکتور Q را کاملا قابل تنظیم کنیم، در این صورت میتوانیم این دو مقاومت فیدبک را با یک پتانسیومتر جایگزین کنیم و آن را به یک بافر اپ امپی دیگر بدهیم تا بهره منفی افزایش یابد. همچنین برای به دست آوردن بیشینه عمق شکاف در فرکانس داده شده، میتوان مقاومتهای و را حذف کرد و پیوند R و 2C را مستقیما به خروجی متصل کرد.
مثال ۲: فیلتر شکافی
یک فیلتر شکافی RC باند باریک با دو اپ امپ را طراحی کنید که فرکانس شکاف مرکزی آن برابر با ۱ کیلو هرتز و پهنای باند 3- دسیبل آن برابر با ۱۰۰ هرتز باشد. از خازن ۰٫۱ میکرو فاراد در مدار خود استفاده کنید و مقدار عمق شکاف مورد انتظار را بر حسب هرتز محاسبه کنید.
حل:
اطلاعات داده شده را میتوان به صورت زیر خلاصه کرد:
ابتدا باید مقدار مقاومت R را برای مقدار خازن داده شده ۰٫۱ میکرو فاراد محاسبه کرد:
در گام بعد نوبت به محاسبه مقدار Q میرسد. برای این کار باید به طریق زیر عمل کنیم:
مقدار سهم فیدبک K را نیز میتوان بر اساس رابطه زیر محاسبه کرد:
حال نوبت به محاسبه مقاومتهای و میرسد:
مقدار مقاومت را برابر با ۱۰ کیلو اهم فرض کنید. در این صورت مقاومت به صورت زیر به دست میآید:
در نهایت میتوانیم مقدار عمق شکاف فیلتر مورد انتظار را به دست آوریم:
مدار فیلتر شکافی که در نهایت طراحی میشود به صورت زیر است.
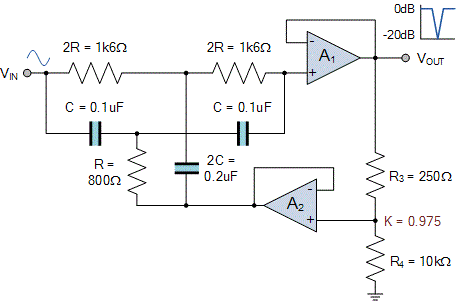
خلاصه فیلتر میان نگذر
در این مطلب به بررسی مدار فیلتر میان نگذر پرداختیم و دیدیم که در یک فیلتر میان نگذر ایدهآل پاسخ فرکانسی دقیقا برعکس پاسخ فرکانسی فیلتر میان گذر است. فیلترهای میان نگذر فرکانسهایی را که در بازه بین دو فرکانس قطع خود، یعنی و قرار دارند را مسدود یا رد میکنند، اما فرکانسهای دو طرف خارج از این بازه را به راحتی عبور میدهند. به بازه فرکانسهای بزرگتر از و کوچکتر از ، باند توقف فیلتر میان نگذر میگویند.
یک فیلتر میان نگذر برای عملکرد خود، مخصوصا در طراحی پهن باند، خروجی یک فیلتر بالا گذر را با خروجی یک فیلتر پایین گذر جمع میکند. یک طراحی فیلتر میان نگذر با باند توقف پهن را با نام فیلتر حذف باند نیز میشناسند و یک فیلتر میان نگذر با باند توقف باریک، فیلتر شکافی نام دارد. در هر کدام از این حالتها، یک فیلتر میان نگذر مداری مرتبه دو به حساب میآید.
فیلترهای شکافی به این منظور طراحی میشوند که بتوانند تضعیف بسیار بالایی را در یک فرکانس خاص و مقادیر نزدیک به آن ایجاد کنند و در سایر فرکانسها تضعیف بسیار کمی، در حد صفر به وجود بیاورند. فیلترهای شکافی در مدار خود از دو شبکه مقاومت و خازن (RC) استفاده میکننده که به صورت موازی با هم قرار گرفتهاند و به آن مدار T دوقلو میگویند. این مدار قادر است شکاف عمیقی را در پاسخ فرکانسی فیلتر ایجاد کند. میتوان از طریق بازخوراندن بخشی از خروجی به محل پیوند دو T، مقادیر بزرگ تر Q را به دست آورد.
برای اینکه یک فیلتر شکافی قدرت گزینشگری بالاتری داشته باشد و بتوان مقادیر Q را تنظیم کرد، میتوانیم محل پیوند خازن و مقاومت را در دو مدار T شکل به نقطه مرکزی مدار مقسم ولتاژ متصل کنیم که به سیگنال خروجی فیلتر وصل شده است. یک فیلتر شکافی که طراحی مناسبی داشته باشد، میتواند تضعیفهای بیشتر از 60- دسیبل در فرکانس شکاف را ایجاد کند.
فیلترهای میان نگذر در مدارهای الکترونیکی و نیز مخابراتی کاربردهای فراوانی دارند و همان طور که در اینجا دیدیم، این فیلترها قادرند یک باند از فرکانسهای ناخواسته را از یک سیستم حذف کنند، در حالی که به سایر فرکانسها اجازه عبور با کمینه تضعیف و اتلاف را میدهند. فیلترهای شکافی نیز قدرت گزینشگری بسیار بالایی دارند و میتوانند به صورتی طراحی شوند که یک فرکانس یا محتوای هارمونیک خاصی را تضعیف کنند که نویز الکتریکی تولید میکند.
اگر این مطلب برای شما مفید بوده است، مطالب و آموزشهای زیر نیز برای مطالعه بیشتر به شما پیشنهاد میشوند:
- مجموعه آموزشهای مهندسی برق
- آموزش الکترونیک ۳
- مجموعه آموزشهای مهندسی مخابرات
- آموزش طراحی فیلتر و سنتز مدار
- مبدل فرکانس به ولتاژ چیست و چگونه کار میکند؟ — از صفر تا صد
- پهنای باند معادل نویز (ENBW) چیست؟ — از صفر تا صد
- مدولاسیون کد پالس (PCM) چیست؟ — از صفر تا صد
^^













اگه به جای استفاده از دو تا خازن و دو تا مقاومت از سلف و خازن و مقاومت استفاده کنیم چطور باید فرکانس قطع رو به دست آورد ؟ و پهنای باند رو