فیلتر میان گذر اکتیو — از صفر تا صد
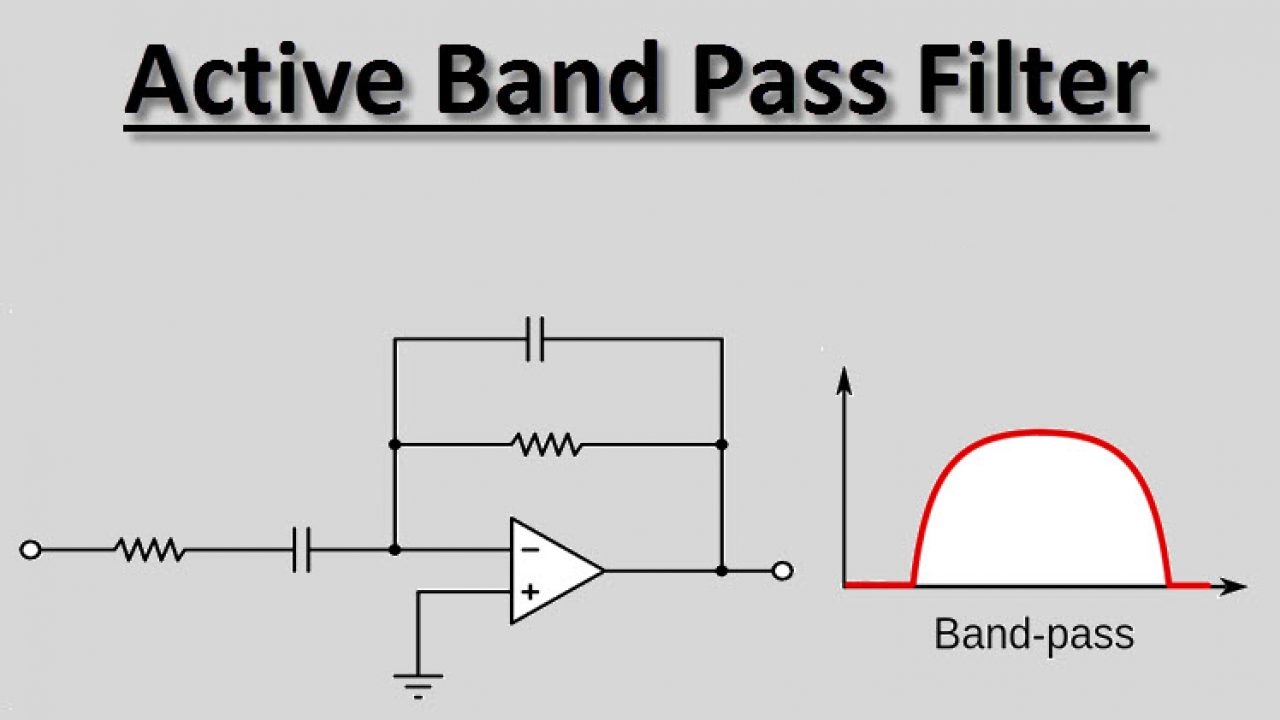
در مطالب قبلی مجله فرادرس به بررسی انواع فیلترهای بالا گذر و پایین گذر و میان گذر پسیو پرداختیم و بیان کردیم که ضعف عمده فیلترهای پسیو، عدم وجود توانایی تقویتکنندگی در آنها است. به همین دلیل، با استفاده از یک تقویتکننده عملیاتی یا اپ امپ در مدار فیلترهای پسیو این مشکل را برطرف کردیم و نوع جدید فیلترها، یعنی فیلتر بالا گذر اکتیو و فیلتر پایین گذر اکتیو را به وجود آوریم. در این مطلب قصد داریم به بررسی نوع دیگری از فیلترهای اکتیو بپردازیم که «فیلتر میان گذر اکتیو» (Active Band Pass Filter) نام دارد.
مهمترین مشخصه یک فیلتر میان گذر یا هر فیلتر دیگری، توانایی آن در عبور فرکانسهای تضعیف نشده (Unattenuated) در طول یک بازه خاص یا یک گستره فرکانسی است که به آن «باند عبور» (Pass Band) میگویند. برای یک فیلتر پایین گذر، باند عبور از حدود فرکانس صفر هرتز یا DC شروع میشود و تا نقطه فرکانس قطع مشخصی ادامه مییابد که $$ -3dB $$ پایینتر از بهره باند عبور بیشینه قرار دارد. به طریق مشابه، در یک فیلتر بالا گذر، باند عبور از همین نقطه فرکانس قطع $$ -3dB $$ شروع میشود و در یک فیلتر نوع پسیو تا بینهایت و در فیلتر نوع اکتیو تا بیشینه بهره حلقه باز ادامه مییابد.
اما فیلتر میان گذر اکتیو نسبت به فیلترهای پایین گذر اکتیو و یا فیلترهای بالا گذر اکتیو اندکی متفاوت عمل میکند. فیلتر میان گذر اکتیو یک مدار «انتخابگر فرکانس» (Frequency Selective) است که در سیستمهای الکترونیکی به منظور جداسازی یک سیگنال از فرکانسهای خاصی مورد استفاده قرار میگیرد.
همچنین میتوان گفت که کارکرد این فیلتر این است که یک گستره از سیگنالها که دارای بازه فرکانسی خاصی هستند را از سایر سیگنالها با فرکانسهای دیگر تفکیک کند. این باند یا گستره فرکانسی بین دو «نقطه قطع فرکانسی» (Cut-off Frequency Point) یا «نقطه فرکانس گوشه» (Corner Frequency Point) قرار گرفته است که به یکی از این نقاط، «فرکانس پایین» (Lower Frequency) و به دیگر «فرکانس بالا» (Higher Frequency) میگویند.
فیلتر میان گذر اکتیو
یک فیلتر میان گذر اکتیو ساده را میتوان با اتصال آبشاری یک فیلتر بالا گذر پسیو و یک فیلتر پایین گذر پسیو به یک تقویتکننده ایجاد کرد.
در تصویر زیر یک بلوک دیاگرام از نحوه تشکیل یک فیلتر میان گذر اکتیو نشان داده شده است.

فرکانس قطع یا گوشه مربوط به فیلتر پایین گذر یا LPF باید بالاتر از فرکانس قطع فیلتر بالا گذر یا HPF باشد. توجه کنید که اختلاف بین دو فرکانس در نقطه $$ -3dB $$، پهنای باند فیلتر میان گذر اکتیو را تعیین میکند، در حالی که هر فرکانسی خارج از این باند فرکانسی توسط فیلتر به شدت تضعیف میشود. همان طور که گفتیم برای ساخت فیلتر میان گذر اکتیو ساده میتوانیم یک فیلتر بالا گذر را به یک فیلتر پایین گذر متصل کنیم و در بین این دو فیلتر از یک تقویتکننده عملیاتی یا اپ امپ استفاده کنیم. در تصویر زیر نمایی از مدار یک فیلتر میان گذر اکتیو نشان داده شده است.
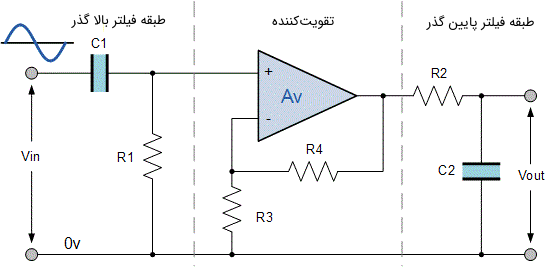
اتصال آبشاری یک فیلتر بالا گذر پسیو و یک فیلتر پایین گذر پسیو به یکدیگر، یک مدار فیلتر با فاکتور Q پایین ایجاد میکند که دارای باند عبور گستردهای است. اولین طبقه از فیلتر میان گذر اکتیو، طبقه فیلتر بالا گذر است که از یک خازن برای مسدود کردن هر بایاس DC از منبع استفاده میکند. یک مزیت بسیار مهم این نوع طراحی در این است که یک پاسخ فرکانسی با باند عبور متقارن و مسطح تولید میکند که نصفی از آن نشان دهنده پاسخ فیلتر پایین گذر و نصف دیگر آن نشان دهنده پاسخ فیلتر بالا گذر است. در تصویر زیر پاسخ فرکانسی یک فیلتر میان گذر اکتیو نشان داده شده است.
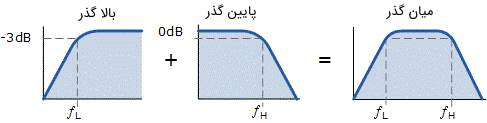
توجه کنید که در مدار فیلتر میان گذر اکتیو فوق، نقطه فرکانس قطع پایین $$ f _ L $$ و نقطه فرکانس قطع بالا $$ f _ H $$، همانند روشهای قبلی در فیلترهای پایین گذر و بالا گذر استاندار مرتبه اول محاسبه میشوند. واضح است که یک تفکیک منطقی بین دو فرکانس قطع بالا و پایین مورد نیاز است تا از هرگونه اثر متقابل بین دو طبقه فیلتر بالا گذر و فیلتر پایین گذر جلوگیری شود. همچنین استفاده از اپ امپ بین دو طبقه، ایزولاسیون الکتریکی خوبی را به وجود می آورد و علاوه بر این، بهره ولتاژ کلی مدار را تعریف میکند.
پهنای باند فیلتر به صورت اختلاف بین دو نقطه $$ -3dB $$ بالا و پایین محاسبه میشود. به عنوان مثال، فرض کنید که یک فیلتر میان گذر در اختیار داریم که نقطه فرکانس قطع پایین آن برابر با $$ 200 Hz $$ است و نقطه فرکانس قطع بالای آن در $$ 600 Hz $$ قرار دارد. بنابراین پهنای باند فیلتر را با استفاده از رابطه زیر میتوانیم محاسبه کنیم:
$$ Bandwidth \; (BW) \; = \; 600 – 200 \; = \; 400 \; Hz $$
پاسخ فرکانسی و شیفت فاز نرمال شده برای یک فیلتر میان گذر اکتیو در تصویر زیر نشان داده شده است.
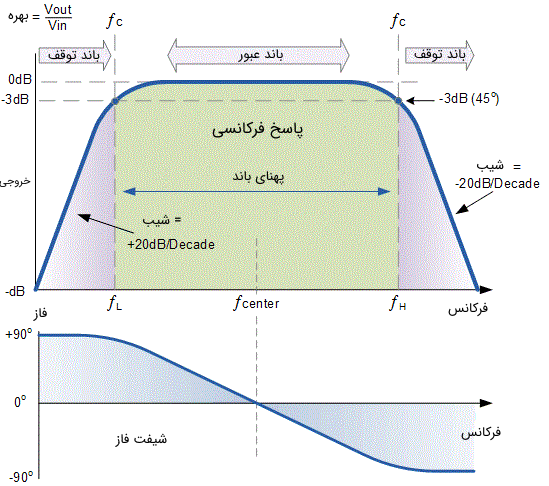
زمانی که مدار فیلتر تنظیم شده فوق به عنوان یک فیلتر میان گذر اکتیو عمل کند، باند عبور یا پهنای باند میتواند بسیار گسترده باشد و این خود میتواند مشکلساز باشد؛ زیرا امکان دارد ما نیاز به ایزولاسیون باند فرکانسی کوچکی داشته باشد. فیلتر میان گذر اکتیو را با استفاده از یک تقویت کننده عملیاتی معکوس کننده نیز میتوان پیادهسازی کرد.
در تصویر زیر نمایی از یک مدار فیلتر میان گذر اکتیو معکوس کننده نشان داده شده است.
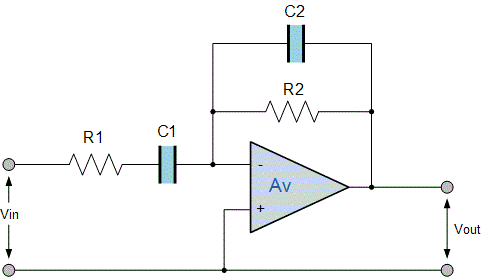
حال با استفاده از چیدمان مجدد و تغییر موقعیت قرارگیری مقاومت و خازن در مدار فیلتر، میتوانیم یک فیلتر بهتر با عملکرد بالاتر را ایجاد کنیم. برای یک فیلتر میان گذر اکتیو، نقطه فرکانس قطع $$ -3dB $$ پایین را با $$ f _ { C 1 } $$ و نقطه فرکانس قطع $$ -3dB $$ بالا را با $$ f _ { C 2 } $$ نشان میدهیم. بهره ولتاژ و نقاط قطع بالا و پایین را به صورت زیر میتوان محاسبه کرد:
$$ \text { voltage gain }= \; - \;\frac { R _ 2 } { R _ 1 } $$
$$ f _ { C 1 } = \frac { 1 } { 2 \pi R _ 1 C _ 1} $$
$$ f _ { C 2 } = \frac { 1 } { 2 \pi R _ 2 C _ 2} $$
توجه کنید که این نوع از فیلترها به این دلیل مورد استفاده قرار میگیرند که دارای باند عبور بسیار باریکی هستند. فرکانس مرکزی و پهنای باند فیلتر میان گذر اکتیو با مقادیر $$ R _ 1 $$ و $$ R _ 2 $$ و $$ C _ 1 $$ و $$ C _ 2 $$ مرتبط هستند. خروجی مدار فیلتر را مجددا از خروجی اپ امپ دریافت میکنیم.
فیلتر میان گذر اکتیو با فیدبک چندگانه
حال فیلتر میان گذر اکتیو ساده فوق را میتوانیم مجددا از طریق بازآرایی اجزای آن بهبود دهیم تا یک فیلتر میان گذر اکتیو با «بهره بینهایت و فیدبک چند گانه» (Infinite-Gain Multiple-Feedback) یا IGMF ایجاد شود. این طراحی از فیلتر میان گذر اکتیو، یک مدار مبتنی بر تنظیم را در اطراف یک فیلتر اکتیو با فیدبک منفی تشکیل میدهد که به آن پاسخ دامنه با فاکتور Q بالایی (بالاتر از ۲۵) میدهد و نیز شیب «رول آف» (Roll-off) را در هر دو طرف از فرکانس مرکزی تندتر میکند.
به دلیل اینکه پاسخ فرکانسی این مدار بسیار شبیه به پاسخ فرکانسی «مدار رزونانس» (Resonance Circuit) است، به فرکانس مرکزی، فرکانس رزونانس $$ f _ r $$ نیز میگویند. در تصویر زیر نمایی از یک مدار فیلتر میان گذر اکتیو با بهره بینهایت و فیدبک چندگانه نشان داده شده است.
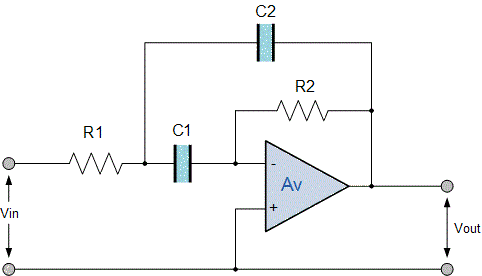
این مدار فیلتر میان گذر اکتیو از تمام بهره تقویتکننده عملیاتی استفاده میکند و در این مدار چند فیدبک منفی از طریق مقاومت $$ R _ 2 $$ و خازن $$ C _ 2 $$ اعمال شدهاند. حال مشخصههای فیلتر میان گذر اکتیو با بهره بینهایت و فیدبک چندگانه یا IGMF را میتوان به طریق زیر تعریف کرد:
$$ f _ r = \frac { 1 } { 2 \pi \sqrt{ R _ 1 R _ 2C _ 1 C _ 2 } } $$
$$ Q _ { BP } = \frac { f _ r } { BW _ { 3 dB } } = \frac { 1 } { 2 } \frac { R _ 2 } { R _ 1 } $$
$$ \text { maximum gain, (AV) } = - \frac { R _ 2 } {2 R _ 1 } = -2 Q ^ 2 $$
حال با توجه به فرمولهای فوق میتوان دید که رابطه بین مقاومتهای $$ R _ 1 $$ و $$ R _ 2 $$ مقدار فاکتور Q باند گذر و فرکانسی را تعیین میکند که در آن بیشینه دامنه به وقوع میپیوندد. در این فرکانس بهره مدار تقویتکننده برابر با $$ -2 Q ^ 2 $$ محاسبه میشود. بنابراین میتوان گفت که هرچه بهره مدار افزایش یابد، گزینشگری فیلتر نیز بهبود مییابد (هرچه بهره بزرگتر باشد، تفکیک فیلتر میان گذر نیز بالاتر است).
مثال فیلتر میان گذر اکتیو
یک فیلتر میان گذر اکتیو که دارای بهره ولتاژ $$ A _ V $$ واحد و فرکانس رزونانس $$ f _ r $$ یک کیلو هرتز باشد، با استفاده از یک مدار فیلتر بهره بینهایت فیدبک چندگانه ایجاد شده است. مقادیر المانهای مورد نیاز برای ساخت چنین فیلتری را به دست آورید.
حل:
ابتدا میتوانیم مقادیر دو مقاومت $$ R _ 1 $$ و $$ R _ 2 $$ مورد نیاز در ساخت مدار فیلتر را محاسبه کنیم. برای این کار میتوانیم مانند زیر از بهره فیلتر در یافتن مقدار Q استفاده کنیم:
$$ A _ V = 1 = - 2 Q ^ 2 $$
$$ Q _ { BP } = \sqrt { \frac { 1 } { 2 } } = 0.7071 $$
$$ Q = 0.7071 = \frac { 1 } { 2 } \sqrt { \frac { R _ 2 } { R _ 1 } } $$
$$ \therefore \frac { R _ 2 } { R _ 1 } = ( \frac { 0.7071 } { \frac { 1 } { 2 } } ) ^ 2 = 2 $$
بنابراین میتوانیم ببینیم که با استفاده از مقدار Q برابر با ۰٫۷۰۷۱ توانستیم رابطه بین مقدار مقاومت $$ R _ 2 $$ و $$ R _ 1 $$ را به دست آوریم. در واقع مقدار مقاومت $$ R _ 2 $$ باید دو برابر مقاومت $$ R _ 1 $$ باشد و به همین دلیل میتوانیم هر مقدار مناسب برای این مقاومتها را انتخاب کنیم، به شرط اینکه نسبت دو بین آنها برقرار باشد. به عنوان مثال، مقدار مقاومت $$ R _ 1 $$ را برابر با ۱۰ کیلو اهم و مقدار مقاومت $$ R _ 2 $$ را برابر با ۲۰ کیلو اهم در نظر میگیریم.
فرکانس مرکزی یا فرکانس رزونانس فیلتر میان گذر اکتیو برابر با ۱ کیلو هرتز فرض شده است. حال با استفاده از مقادیر مقاومتهای به دست آمده، میتوانیم مقدار خازنهای مورد نیاز را با فرض $$ C = C _ 1 = C _ 2 $$ محاسبه کنیم:
$$ f _ r = 1000 HZ = \frac { 1 } { 2 \pi C \sqrt{ R _ 1 R _ 2 } } $$
$$ \therefore C = \frac { 1 } { 2 \pi f _ r \sqrt{ R _ 1 R _ 2 } } = \frac { 1 } { 2 \pi 1000 \sqrt{ 10000 * 20000 } } = 11.2 nF $$
نزدیکترین مقدار استاندارد به خازن به دست آمده برابر با ۱۰ نانو فاراد است.
نقطه فرکانس رزونانس
شکل واقعی منحنی پاسخ فرکانسی هر فیلتر میان گذر پسیو یا اکتیو، به مشخصههای مدار فیلتر بستگی دارد. در واقع نمودار پاسخ فرکانسی که در بالا برای فیلتر میان گذر ترسیم شد، به عنوان یک پاسخ فرکانسی میان گذر ایدهآل تعریف میشود. فیلتر میان گذر اکتیو، یک فیلتر از نوع درجه دو است؛ زیرا در طراحی مداری خود، دارای دو المان اکتیو (دو خازن) است.
به دلیل وجود دو المان فعال، پاسخ پیک یا فرکانس رزونانس $$ f _ r $$ فیلتر میان گذر اکتیو در فرکانس مرکزی یا $$ f _ c $$ قرار گرفته است. فرکانس مرکزی معولا به صورت میانگین هندسی دو فرکانس $$ -3dB $$ و در بین نقطه قطع بالا و نقطه قطع پایین محاسبه میشود. در نتیجه فرکانس رزونانس به صورت زیر به دست می آید:
$$ f _ r = \sqrt { f _ L \times f _ H } $$
در این رابطه، $$ f _ r $$ برابر با فرکانس مرکزی یا رزونانس، $$ f _ L $$ نقطه فرکانس قطع $$ -3dB $$ پایین و $$ f _ H $$ نقطه فرکانس قطع $$ -3dB $$ بالا است.
در مثال سادهای که در قسمت قبلی بیان کردیم، فرکانس قطع $$ -3dB $$ پایین برابر با ۲۰۰ هرتز و فرکانس قطع $$ -3dB $$ بالا برابر با ۶۰۰ هرتز فرض شده بود. بنابراین میتوان گفت که در فیلتر میان گذر اکتیو ایجاد شده، فرکانس رزونانس یا فرکانس مرکزی برابر است با:
$$ f _ r = \sqrt { 200 \times 600 } = \sqrt { 120000 } = 346 HZ $$
فاکتور Q در فیلتر میان گذر اکتیو
در مدار یک فیلتر میان گذر اکتیو، عرض کلی باند عبور واقعی بین دو نقطه فرکانس قطع $$ -3dB $$ پایین و نقطه فرکانس قطع $$ -3dB $$ بالا تعیین کننده فاکتور Q یا «فاکتور کیفیت» (Quality Factor) مدار فیلتر است. توجه کنید که فاکتور کیفیت در یک فیلتر پایین گذر اکتیو معیاری است برای تعیین این که فیلتر نسبت به بازه فرکانسی ورودی به آن تا چه اندازه باند عبور گزینشگر یا «غیر گزینشگری» (Un-selective) دارد.
هرچه فاکتور Q در فیلتر پایینتر باشد، پهنای باند فیلتر میان گذر اکتیو پهنتر است و هر چه مقدار فاکتور Q بزرگتر باشد، فیلتر میان گذر باند عبور باریکتری دارد و به عبارت دیگر، فیلتر میان گذر گزینشیتر عمل میکند. فاکتور کیفیت یک فیلتر میان گذر را گاهی اوقات با حرف یونانی $$ \alpha $$ نمایش میدهند و به آن «فرکانس پیک آلفا» (Alpha Peak Frequency) میگویند. رابطه بین $$ \alpha $$ و فاکتور Q به صورت زیر نوشته میشود:
$$ \alpha = \frac { 1 } { Q } $$
چون فاکتور کیفیت یک فیلتر میان گذر اکتیو (سیستم مرتبه دوم) به شیب پاسخ فرکانسی فیلتر در اطراف فرکانس نوسان مرکزی $$ f _ r $$ آن وابسته است، در نتیجه میتوان فاکتور کیفیت را به صورت فاکتور میرایی یا «ضریب میرایی» (Damping Coefficient) نیز در نظر گرفت. زیرا هر اندازه که فیلتر میرایی بالاتری داشته باشد، پاسخ فرکانسی آن مسطحتر است و هر اندازه که سیستم میرایی ضعیفتری داشته باشد، از مسطح بودن پاسخ فرکانسی نیز کاسته میشود و تیزتر میشود. فاکتور ضریب میرایی را با نماد $$ \xi $$ نشان میدهند و بر اساس رابطه زیر محاسبه میکنند:
$$ \xi = \frac { \alpha } { 2 } $$
فاکتور Q مربوط به یک فیلتر میان گذر برابر با نسبت فرکانس رزونانس $$ f _ r $$ به پهنای باند بین فرکانسهای $$ -3dB $$ بالا و پایین است. به این نکته توجه کنید که فاکتور کیفیت بدون واحد است:
$$ Q = \frac { \text { Resonant Frequency } } { \text { Bandwidth } } $$
در تصویر زیر ارتباط بین فاکتور کیفیت در فیلتر میان گذر اکتیو و پهنای باند آن نشان داده شده است.
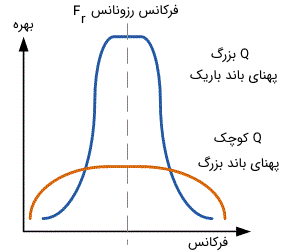
بنابراین برای فیلتر میان گذر اکتیو ساده مثال بخشهای قبل، فاکتور کیفیت یا Q را میتوان به طریق زیر محاسبه کرد:
$$ Q = \frac { 346 HZ } { 400 HZ } = 0.865 $$
هنگامی که عملکرد یک فیلتر میان گذر اکتیو را آنالیز میکنیم، معمولا یک فیلتر نرمال شده را در نظر میگیریم که پاسخ فرکانسی ایدهآل تولید میکند. پاسخ فرکانسی ایدهآل به این صورت فرض میشود که شکل مستطیلی دارد و زمان انتقال بین باند عبور و باند توقف بسیار سریع و نیز شیب رول آف بسیار تند است. اما نکتهای که وجود دارد این است که تولید پاسخ فرکانسی این چنین ایدهآل در واقعیت و در مدارهای عملی امکان پذیر نیست. بنابراین باید از تقریب استفاده کنیم تا بهترین پاسخ فرکانسی ممکن متناسب با فیلتری که در حال طراحی آن هستیم را در اختیار ما قرار دهد. احتمالا بهترین و شناخته شدهترین تقریب فیلتر برای این کار، «فیلتر باترورث» (Butterworth) یا «فیلتر پاسخ مسطح بیشینه» (Maximally Flat Response Filter) است.
اگر این مطلب برای شما مفید بوده است، مطالب و آموزشهای زیر نیز برای مطالعه بیشتر به شما پیشنهاد میشوند:
- مجموعه آموزشهای مهندسی برق
- آموزش الکترونیک ۳
- مجموعه آموزشهای مهندسی مخابرات
- آموزش طراحی فیلتر و سنتز مدار
- تقویت کننده لگاریتمی و آنتی لگاریتمی — از صفر تا صد
- اسیلاتور کنترل شده با ولتاژ (VCO) — از صفر تا صد
- تشخیص عیب (Fault Detection) — از صفر تا صد
^^










